Производительность и моделирование передачи переменного тока

Результат моделирования модели линии без потерь (в PSpice )

Моделирование производительности — это абстракция реальной системы в упрощенное представление, позволяющее прогнозировать производительность. ^[1] Создание модели может дать представление о том, как будет или работает предлагаемая или фактическая система. Однако это может указывать на разные вещи людям, принадлежащим к разным сферам деятельности.

Моделирование производительности имеет множество преимуществ, в том числе:

Относительно недорогое предсказание будущих результатов.
Более четкое понимание характеристик производительности системы.
Кроме того, он может включать механизм управления и снижения рисков с поддержкой проектирования будущих проектов.

Модель часто создается специально для того, чтобы ее можно было интерпретировать программным инструментом, моделирующим поведение системы на основе информации, содержащейся в модели производительности. Такие инструменты обеспечивают более глубокое понимание поведения системы и могут использоваться для выявления узких мест или горячих точек, где конструкция неадекватна. Решения выявленных проблем могут включать предоставление дополнительных материальных ресурсов или изменение структуры проекта.

Моделирование производительности оказывается полезным в случае:

Оценка производительности новой системы.
Оценка влияния на производительность существующей системы при взаимодействии с ней новой системы.
Оценка влияния изменения рабочей нагрузки или входных данных на существующую систему.

Моделирование линии электропередачи проводится для анализа ее производительности и характеристик. Собранная информация, моделирующая модель, может быть использована для уменьшения потерь или для компенсации этих потерь. Более того, это дает больше информации о работе линий электропередачи и помогает найти способ повысить общую эффективность передачи с минимальными затратами.

Обзор

Передача электроэнергии — это массовое перемещение электрической энергии от генерирующего объекта, такого как электростанция , к электрической подстанции , и она отличается от местной проводки между высоковольтными подстанциями и потребителями, которую обычно называют распределением электроэнергии . Взаимосвязанная сеть, которая облегчает это движение, известна как линия передачи. Линия передачи — это набор электрических проводников, по которым электрический сигнал передается из одного места в другое. Примерами являются коаксиальный кабель и витая пара. Линия электропередачи способна передавать электроэнергию из одного места в другое. Во многих электрических цепях длиной проводов, соединяющих компоненты, по большей части можно пренебречь. То есть напряжение на проводе в данный момент времени можно считать одинаковым во всех точках. Однако, когда напряжение изменяется за интервал времени, сравнимый со временем, необходимым для прохождения сигнала по проводу, длина становится важной, и провод следует рассматривать как линию передачи. Другими словами, длина провода важна, когда сигнал включает в себя частотные составляющие с соответствующими длинами волн, сравнимыми или меньшими длины провода. На сегодняшний день линии электропередачи классифицированы и определены по-разному. Несколько подходов к моделированию также реализуются с использованием различных методов. Большинство из них являются математическими и предполагаемыми моделями, основанными на схемах.

Трансмиссия может быть двух типов:

Передача HVDC (передача постоянного тока высокого напряжения)
Передача HVAC (передача переменного тока высокого напряжения)

Высоковольтная передача постоянного тока

Постоянный ток высокого напряжения (HVDC) используется для передачи больших объемов энергии на большие расстояния или для соединения между асинхронными сетями. Когда электрическую энергию необходимо передавать на очень большие расстояния, потери мощности при передаче переменного тока становятся значительными, и использование постоянного тока вместо переменного тока обходится дешевле . ^[2] Для очень длинной линии передачи эти более низкие потери (и снижение стоимости строительства линии постоянного тока) могут компенсировать дополнительные затраты на необходимые преобразовательные станции на каждом конце. В линии передачи постоянного тока ртутный дуговой выпрямитель преобразует переменный ток в постоянный. . ^[3] Линия передачи постоянного тока передает большую мощность на большие расстояния. На стороне потребителя тиратрон преобразует постоянный ток в переменный. ^[4]

трансмиссия системы отопления, вентиляции и кондиционирования воздуха

Линия передачи переменного тока используется для передачи основной части мощности, вырабатываемой на стороне потребителя. ^[5] Электроэнергия вырабатывается на электростанции. Линия электропередачи передает электроэнергию от генерации к потребителю. Передача энергии высокого напряжения позволяет снизить резистивные потери на большие расстояния в проводке. ^[5] Такая эффективность передачи высокого напряжения позволяет передавать большую часть генерируемой мощности на подстанции и, в свою очередь, на нагрузки, что приводит к экономии эксплуатационных затрат. Мощность передается от одного конца к другому с помощью повышающего и понижающего трансформатора. высокого напряжения Большинство линий электропередачи представляют собой трехфазный переменный ток (AC), хотя однофазный иногда используется в системах электрификации железных дорог переменный ток . Электричество передается при высоком напряжении (115 кВ или выше), чтобы уменьшить потери энергии, возникающие при передаче на большие расстояния.

Электроэнергия обычно передается по воздушным линиям электропередачи . ^[6] Подземная передача электроэнергии имеет значительно более высокую стоимость установки и более серьезные эксплуатационные ограничения. ^[6] но снижает затраты на техническое обслуживание. ^[7] Подземная передача иногда используется в городских районах или экологически чувствительных местах. ^[7]

Терминология

Линия без потерь

Волна, бегущая вправо по линии передачи без потерь. Черные точки представляют электроны, а стрелки показывают электрическое поле.

Приближение линии без потерь является наименее точной моделью; его часто используют на коротких линиях, когда индуктивность линии значительно превышает ее сопротивление. В этом приближении напряжение и ток идентичны на передающем и принимающем концах.

Характеристическое сопротивление является чисто реальным, что означает резистивное сопротивление для этого сопротивления, и его часто называют импульсным сопротивлением для линии без потерь. Когда линия без потерь завершается импульсным сопротивлением, падения напряжения нет. Хотя фазовые углы напряжения и тока изменяются, величины напряжения и тока остаются постоянными по длине линии. При нагрузке > SIL напряжение на передающем конце упадет, и линия будет «потреблять» ВАР. При нагрузке < SIL напряжение будет увеличиваться с передающего конца, и линия будет генерировать ВАР.

Коэффициент мощности

В электротехнике коэффициент мощности электроэнергетической системы переменного тока определяется как отношение реальной мощности, поглощаемой нагрузкой , к полной мощности, протекающей в цепи, и представляет собой безразмерное число в замкнутом интервале от -1 до 1. Коэффициент мощности меньше единицы указывает на то, что напряжение и ток не совпадают по фазе, что уменьшает мгновенное произведение этих двух значений. Отрицательный коэффициент мощности возникает, когда устройство (которое обычно является нагрузкой) генерирует мощность, которая затем течет обратно к источнику.

Реальная мощность представляет собой мгновенное произведение напряжения и тока и представляет собой способность электричества выполнять работу.
Полная мощность представляет собой среднее произведение тока и напряжения. Из-за энергии, накопленной в нагрузке и возвращаемой к источнику, или из-за нелинейной нагрузки, которая искажает форму волны тока, потребляемого от источника, полная мощность может быть больше реальной мощности (pf ≤0,5).

В электроэнергетической системе нагрузка с низким коэффициентом мощности потребляет больший ток, чем нагрузка с высоким коэффициентом мощности при том же объеме передаваемой полезной мощности. Более высокие токи увеличивают потери энергии в распределительной системе и требуют более толстых проводов и другого оборудования. Из-за стоимости более крупного оборудования и потерь энергии электроэнергетические компании обычно взимают более высокую плату с промышленных или коммерческих потребителей, где коэффициент мощности низкий.

Импеданс перенапряжения

Импедансная нагрузка на линии без потерь

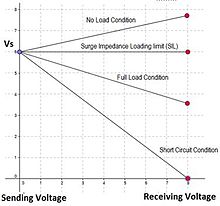
Характеристическое сопротивление или волновое сопротивление (обычно обозначаемое Z ₀ ) однородной линии передачи представляет собой отношение амплитуд напряжения и тока одной волны, распространяющейся по линии; то есть волна, бегущая в одном направлении при отсутствии отражений в другом направлении. Альтернативно и эквивалентно его можно определить как входное сопротивление линии передачи, когда ее длина бесконечна. Характеристическое сопротивление определяется геометрией и материалами линии передачи и для однородной линии не зависит от ее длины. Единицей характеристического сопротивления в системе СИ является Ом (Ом).

Импеданс импульса определяет нагрузочную способность линии и коэффициент отражения распространяющихся волн тока или напряжения. $Z_{0}={\sqrt {\frac {L}{C}}}$

Где,

Z ₀ = характеристическое сопротивление линииL = Индуктивность на единицу длины линииC = Емкость на единицу длины линии

Параметры линии

Линия передачи имеет в основном четыре параметра: сопротивление, индуктивность, емкость и шунтирующую проводимость. ^[8] Эти параметры равномерно распределены по линии. Следовательно, его также называют распределенным параметром линии передачи.

Эффект Ферранти

В электротехнике — эффект Ферранти это увеличение напряжения, происходящее на приемном конце очень длинной (>200 км) переменного тока линии электропередачи , относительно напряжения на передающем конце, когда нагрузка очень мала или отсутствует. нагрузка подключена. Его можно выразить как коэффициент или как процентное увеличение: ^[9]

Зарядный ток емкостной линии вызывает падение напряжения на индуктивности линии, которое синфазно с напряжением на передающем конце, при условии незначительного сопротивления линии. Следовательно, за это явление ответственны как индуктивность линии, так и емкость. Это можно проанализировать, рассматривая линию как линию передачи , в которой полное сопротивление источника ниже, чем полное сопротивление нагрузки (незаземленное). Эффект аналогичен электрически короткой версии четвертьволнового трансформатора сопротивления , но с меньшим преобразованием напряжения.

Эффект Ферранти тем более выражен, чем длиннее линия и чем выше приложенное напряжение. ^[10] Относительное повышение напряжения пропорционально квадрату длины линии и квадрату частоты. ^[11]

Эффект Ферранти гораздо более выражен в подземных кабелях, даже небольшой длины, из-за их высокой емкости на единицу длины и более низкого электрического сопротивления .

Коронный разряд

Коронный разряд — это электрический разряд, вызванный ионизацией жидкости , например воздуха, окружающей проводник заряженный электрически . Спонтанные коронные разряды естественным образом возникают в высоковольтных системах, если не принять меры по ограничению напряженности электрического поля . Корона возникает, когда сила электрического поля ( градиент потенциала ) вокруг проводника достаточно высока, чтобы образовать проводящую область, но недостаточно высока, чтобы вызвать электрический пробой или искрение близлежащих объектов. Его часто можно увидеть как голубоватое (или другого цвета) свечение в воздухе рядом с заостренными металлическими проводниками, несущими высокое напряжение, и оно излучает свет по тем же свойствам, что и газоразрядная лампа .

Во многих приложениях высокого напряжения корона является нежелательным побочным эффектом. Коронный разряд на линиях электропередачи высокого напряжения представляет собой экономически значимую трату энергии. Коронные разряды подавляются за счет улучшенной изоляции, коронирующих колец и изготовления электродов высокого напряжения гладкой закругленной формы.

Параметры ABCD

A, B, C, D — константы, также известные как параметры передачи или параметры цепи. Эти параметры используются для анализа электрической сети. Он также используется для определения характеристик входного, выходного напряжения и тока сети передачи.

Константа распространения

Константа распространения синусоидальной электромагнитной волны является мерой изменения, которому подвергаются амплитуда и фаза волны при ее распространении в заданном направлении. Измеряемой величиной может быть напряжение, ток в цепи или вектор поля, например напряженность электрического поля или плотность потока. Сама константа распространения измеряет изменение на единицу длины, но в остальном она безразмерна. В контексте двухпортовых сетей и их каскадов константа распространения измеряет изменение, которому подвергается исходная величина при ее распространении от одного порта к другому.

Константа затухания

Действительная часть постоянной распространения представляет собой константу затухания и обозначается греческой строчной буквой α (альфа). Это приводит к уменьшению амплитуды сигнала вдоль линии передачи.

Фазовая постоянная

Мнимая часть постоянной распространения является фазовой постоянной и обозначается греческой строчной буквой β (бета). Это приводит к сдвигу фазы сигнала вдоль линии передачи. Обычно обозначается в радианах на метр (рад/м).

Константа распространения обозначается греческой строчной буквой γ (гамма), причем γ = α + jβ.

Регулирование напряжения

Регулирование напряжения — это мера изменения величины напряжения между передающей и принимающей стороной компонента, такого как линия передачи или распределения. Он указывается в процентах для разных линий.

Математически регулирование напряжения определяется формулой:

$V.R={\frac {V_{no-load}-V_{full-load}}{V_{no-load}}}$

Параметры линии передачи переменного тока

Передача переменного тока имеет четыре линейных параметра: последовательное сопротивление и индуктивность , шунтирующую емкость и допуск . Эти параметры отвечаютдля четкого поведения напряжения и тока форм вдоль линия передачи . Параметры линии обычно представлены в ихсоответствующих единиц на км длины линий электропередачи. Таким образом, эти параметры зависят от геометрического выравнивания трансмиссии.линии (количество используемых проводников , форма проводников, физическое расстояниемежду проводниками и высотой над землей и т. д.). Эти параметрыне зависят от тока и напряжения любого из посылающих илиполучение заканчивается.

Последовательное сопротивление

Определение

Электрическое сопротивление объекта — это свойство вещества, благодаря которому оно ограничивает протекание электрического тока за счет разности потенциалов на двух своих концах. ^[12] Обратная величина равна электрическая проводимость и легкость прохождения электрического тока. Электрическое сопротивление имеет некоторые концептуальные параллели с понятием механического трения . Единицей системе СИ электрического сопротивления в является ом ( Ом ), а электропроводность измеряется в сименсах (См).

Характеристики

Сопротивление объекта во многом зависит от материала, из которого он сделан: объекты, изготовленные из электрических изоляторов, таких как резина, имеют тенденцию иметь очень высокое сопротивление и низкую проводимость, в то время как объекты, изготовленные из электрических проводников, таких как металлы, имеют тенденцию иметь очень низкое сопротивление и высокую проводимость. проводимость. Эта материальная зависимость количественно выражается удельным сопротивлением или проводимостью . Однако сопротивление и проводимость являются обширными, а не объемными свойствами , а это означает, что они также зависят от размера и формы объекта. Например, сопротивление провода выше, если он длинный и тонкий, и ниже, если он короткий и толстый. Все объекты обладают некоторым сопротивлением, за исключением сверхпроводников , сопротивление которых равно нулю.

Сопротивление ( R ) объекта определяется как отношение напряжения на нем ( V ) к току через него ( I ), а проводимость ( G ) является обратным:

R={V \over I},\qquad G={I \over V}={\frac {1}{R}}

Для самых разных материалов и условий V и I прямо пропорциональны друг другу, и поэтому R и G являются константами (хотя они будут зависеть от размера и формы объекта, материала, из которого он изготовлен, и других факторов). например, температура или напряжение). Эта пропорциональность называется законом Ома , а материалы, удовлетворяющие ему, называются омическими материалами. В других случаях, например, в , диоде или батарее , V и I не прямо трансформаторе пропорциональны. Отношение V / I иногда все еще полезно и называется «хордальным сопротивлением» или «статическим сопротивлением». ^[13]^[14] поскольку он соответствует обратному наклону хорды между началом координат ВАХ и . В других ситуациях производная ${\frac {dV}{dI}}\,\!$ может быть наиболее полезным; это называется «дифференциальным сопротивлением».

Линии электропередачи, состоящие из проводов очень большой длины, обладают электрическим сопротивлением, которым вообще нельзя пренебрегать.

Последовательная индуктивность

Определение

Когда ток течет внутри проводника, возникает магнитный поток. При изменении тока в проводнике меняется и число линий потока, и в нем наводится ЭДС ( закон Фарадея ). Эта наведенная ЭДС представлена параметром, известным как индуктивность. Для обозначения индуктивности принято использовать символ L, в честь физика Генриха Ленца .

В системе СИ единицей индуктивности является генри ( Г ), который представляет собой величину индуктивности, вызывающую напряжение в 1 вольт , когда ток изменяется со скоростью один ампер в секунду. Он назван в честь Джозефа Генри , который открыл индуктивность независимо от Фарадея. ^[15]

Виды индуктивности

Поток, связанный с проводником, состоит из двух частей: внутреннего потока и внешнего потока:

Внутренний поток индуцируется за счет течения тока в проводнике.
Внешний поток, создаваемый вокруг проводника, обусловлен его током и током других проводников, расположенных вокруг него. Полная индуктивность проводника определяется расчетом внутреннего и внешнего потока.

Характеристики

Проводка линии передачи также является индуктивной по своей природе, и индуктивность одной линии цепи может быть определена математически по формуле: $L={\frac {\mu _{0}}{2\pi }}ln{\frac {D}{r\prime }}H/m$

Где,

D — физическое расстояние между проводниками.
$r\prime =re^{-1/4}$ - радиус фиктивного проводника, не имеющего внутренних потокосвязей, но с той же индуктивностью, что и исходный проводник радиуса r. Количество $e^{-1/4}$ (=0,7788 прибл.) умножается на фактический радиус проводника, чтобы учесть внутренние потокосцепления (применимо только к сплошным круглым проводникам). ^[16]
$\mu _{0}$ это проницаемость свободного пространства и ${\mu _{0}}=4\pi \times 10^{-7}H/m$ .

Для транспонированных линий с двумя или более фазами индуктивность между любыми двумя линиями можно рассчитать по формуле: $L={\frac {\mu _{0}}{2\pi }}ln{\frac {D_{GMD}}{r\prime }}H/m$ .

Где, $D_{GMD}$ — среднее геометрическое расстояние между проводниками.

Если линии не транспонированы должным образом, индуктивности становятся неравными и содержат мнимые члены из-за взаимных индуктивностей. В случае правильного транспонирования все проводники занимают доступные позиции на одинаковом расстоянии и, таким образом, мнимые члены сокращаются. И все индуктивности линий становятся равными.

Шунтирующая емкость

Определение

Емкость — это отношение изменения электрического заряда в системе к соответствующему изменению ее электрического потенциала . Емкость зависит только от геометрии конструкции (например, площади пластин и расстояния между ними) и диэлектрической материала между проницаемости диэлектрического пластинами конденсатора. Для многих диэлектрических материалов диэлектрическая проницаемость и, следовательно, емкость не зависят от разности потенциалов между проводниками и общего заряда на них.

Единицей в системе СИ емкости является фарад (обозначение: F), названный в честь английского физика Майкла Фарадея . Конденсатор емкостью 1 фарад, заряженный электрическим зарядом в 1 кулон , имеет разность потенциалов в 1 вольт . между его обкладками ^[17] Обратная величина емкости называется эластичностью .

Типы емкости

Есть два тесно связанных понятия: собственная емкость и взаимная емкость:

Для изолированного проводника существует свойство, называемое собственной емкостью , которое представляет собой количество электрического заряда, которое необходимо добавить к изолированному проводнику, чтобы повысить его электрический потенциал на одну единицу (т.е. на один вольт в большинстве измерительных систем). ^[18] Точкой отсчета для этого потенциала является теоретическая полая проводящая сфера бесконечного радиуса с проводником, расположенным внутри этой сферы. Любой объект, который может быть электрически заряжен, обладает собственной емкостью . Материал с большой собственной емкостью удерживает больше электрического заряда при данном напряжении , чем материал с низкой собственной емкостью.
Понятие взаимной емкости особенно важно для понимания работы конденсатора , одного из трех элементарных линейных электронных компонентов (наряду с резисторами и катушками индуктивности ). В электрических цепях термин «емкость» обычно является сокращением для взаимной емкости между двумя соседними емкостями. проводники, такие как две обкладки конденсатора.

Характеристики

Проводники линии передачи образуют между собой конденсатор , обладающий взаимной емкостью. Проводники линии передачи действуют как параллельные пластины конденсатора, а воздух между ними выступает как диэлектрическая среда. Емкость линии вызывает опережающий ток между проводниками. Это зависит от длины проводника. Емкость линии пропорциональна длине линии передачи. Их влияние незначительно на работоспособность линий малой протяженности и низкого напряжения. В случае высокого напряжения и длинных линий считается ^{[ кем? ]} как один из важнейших параметров. Шунтирующая емкость линии отвечает за эффект Ферранти. ^[19]

Емкость однофазной линии электропередачи может быть определена математически по формуле: $C_{ab}={\frac {\pi \epsilon _{0}}{ln{\frac {D}{r}}}}F/m$

Где,

D — физическое расстояние между проводниками.
r — радиус каждого проводника.
$\epsilon _{0}$ диэлектрическая проницаемость воздуха и ${\epsilon _{0}}=8.854\times 10^{-12}$

Для линий с двумя или более фазами емкость между любыми двумя линиями можно рассчитать с помощью: $C={\frac {\pi \epsilon _{0}}{ln{\frac {D_{GMD}}{r}}}}F/m$

Где, $D_{GMD}$ — среднее геометрическое расстояние проводников.

Эффектом собственной емкости в линии передачи обычно пренебрегают, поскольку проводники не изолированы и, следовательно, не существует обнаруживаемой собственной емкости.

Вход шунта

Определение

В электротехнике проводимость — это мера того, насколько легко цепь или устройство пропускает ток. Он определяется как величина обратная импедансу , . Единицей в системе СИ допуска является сименс (обозначение S); более старая синонимичная единица — mho , а ее символ — ℧ (перевернутая заглавная омега Ω). Оливер Хевисайд ввёл термин «допуск» в декабре 1887 года. ^[20]

Прием определяется как

Y\equiv {\frac {1}{Z}}\,

где

Y — проводимость , измеряется в сименсах.

Z — импеданс , измеряемый в Омах.

Характеристики

Сопротивление — это мера противодействия цепи протеканию постоянного тока, тогда как импеданс учитывает не только сопротивление, но и динамические эффекты (известные как реактивное сопротивление ). Аналогично, проводимость — это не только мера легкости, с которой может течь постоянный ток, но и динамические эффекты восприимчивости материала к поляризации:

Y=G+jB\,

где

$Y$ — адмиттанс, измеряемый в сименсах.
$G$ — проводимость , измеряемая в сименсах.
$B$ — проводимость , измеряемая в сименсах.
$j^{2}=-1$

Динамические эффекты проводимости материала связаны с универсальным диэлектрическим откликом , степенным изменением проводимости системы с частотой в условиях переменного тока.

В контексте электрического моделирования линий электропередачи шунтирующие компоненты, которые обеспечивают пути наименьшего сопротивления в определенных моделях, обычно указываются с точки зрения их проводимости. Линии электропередачи могут простираться на сотни километров, и емкость линии может влиять на уровни напряжения. При анализе линий передачи небольшой длины эту емкость можно игнорировать, и шунтирующие компоненты для модели не нужны. Линии большей длины имеют шунтирующий доступ, определяемый ^[21]

$Y=yl=j\omega Cl$

где

Y – общий доступ шунта

y – проводимость шунта на единицу длины

l – длина линии

C – емкость линии

Моделирование линий электропередачи

Две портовые сети

Двухполюсная сеть (разновидность четырехполюсника или четырехполюсника ) — электрическая сеть ( цепь ) или устройство с двумя парами клемм для подключения к внешним цепям. Две клеммы составляют порт, если приложенные к ним токи удовлетворяют основному требованию, известному как условие порта: электрический ток, входящий в одну клемму, должен быть равен току, выходящему из другой клеммы того же порта. ^[22]^[23] Порты представляют собой интерфейсы, через которые сеть соединяется с другими сетями, точки, где подаются сигналы или принимаются выходные данные. В двухпортовой сети часто порт 1 считается входным, а порт 2 — выходным.

Модель двухпортовой сети используется в методах математического анализа цепей для изоляции частей более крупных цепей. Двухпортовая сеть рассматривается как « черный ящик », свойства которого задаются матрицей чисел . Это позволяет легко рассчитать реакцию сети на сигналы, подаваемые на порты, без учета всех внутренних напряжений и токов в сети. Это также позволяет легко сравнивать аналогичные схемы или устройства. Например, транзисторы часто рассматривают как двухпортовые, характеризующиеся их h-параметрами (см. ниже), указанными производителем. Любую линейную цепь с четырьмя выводами можно рассматривать как двухполюсную сеть при условии, что она не содержит независимого источника и удовлетворяет условиям порта.

Матрица передачи и параметры ABCD

Зачастую для анализа производительности линии нас интересуют только характеристики терминалов линии передачи, то есть напряжение и ток на передающем и принимающем концах. Сама линия передачи затем моделируется как «черный ящик», а для моделирования ее поведения используется матрица передачи 2 на 2, как показано ниже. ^[24]^[25]

{\begin{bmatrix}V_{\mathrm {S} }\\I_{\mathrm {S} }\\\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\\\end{bmatrix}}{\begin{bmatrix}V_{\mathrm {R} }\\I_{\mathrm {R} }\\\end{bmatrix}}

Вывод

Это уравнение в матричной форме состоит из двух отдельных уравнений, как указано ниже: ^[26]

$V_{S}=AV_{R}+BI_{R}$

$I_{S}=CV_{R}+DI_{R}$

Где,

$V_{S}$ это конечное напряжение отправки

$V_{R}$ напряжение на принимающем конце

$I_{S}$ конечный ток отправки

$I_{R}$ это ток принимающей стороны

Теперь, если мы применим разомкнутую цепь на приемной стороне, эффективный ток нагрузки будет равен нулю (т.е. I _R = 0).

1. $A={\frac {V_{S}}{V_{R}}}$

Итак, параметр A представляет собой отношение конечного напряжения отправки к конечному напряжению приема, называемое, таким образом, коэффициентом напряжения. Будучи отношением двух одинаковых величин, параметр А безразмерен.

2. $C={\frac {I_{S}}{V_{R}}}$

Таким образом, параметр C представляет собой отношение конечного тока отправки к конечному напряжению приема, что называется пропускной способностью передачи, а единицей измерения C является Mho ( $\mho$ ).

Теперь, если мы применим короткое замыкание на приемной стороне, эффективное напряжение на приемной стороне будет равно нулю (т.е. V _R = 0).

1. $B={\frac {V_{S}}{I_{R}}}$

Итак, параметр B представляет собой отношение конечного напряжения отправки к конечному току приема, что называется передаточным сопротивлением, а единицей измерения C является Ом ( Ом ).

2. $D={\frac {I_{S}}{I_{R}}}$

Итак, параметр D представляет собой отношение конечного тока отправки к конечному току приема, называемое таким образом коэффициентом тока. Будучи отношением двух одинаковых величин, параметр D безразмерен.

Значения параметра ABCD

Подводя итог, параметры ABCD для пассивной, линейной и двусторонней сети с двумя портами (четырьмя терминалами) задаются как:

Параметры ABCD ^[27]
Параметры	Имя параметра	Ценить	Единица
А	Коэффициент напряжения	$\left.{\frac {V_{S}}{V_{R}}}\right\|_{I_{R}=0}$	На единицу меньше
Б	Передающее сопротивление	$\left.{\frac {V_{S}}{I_{R}}}\right\|_{V_{R}=0}$	Ом (Ώ)
С	Прием трансфера	$\left.{\frac {I_{S}}{V_{R}}}\right\|_{I_{R}=0}$	Более ( $\mho$ )
Д	Коэффициент текущей ликвидности	$\left.{\frac {I_{S}}{I_{R}}}\right\|_{V_{R}=0}$	На единицу меньше

Характеристики

Предполагается, что линия представляет собой взаимную симметричную сеть, а это означает, что метки приема и отправки можно переключать без каких-либо последствий. Матрица передачи T также обладает следующими свойствами:

Константы A, B, C и D являются комплексными числами из-за комплексных значений параметров передачи. А из-за сложной природы они представлены как векторы в комплексной плоскости ( векторы ).
$\det(T)=AD-BC=1$ (Условие взаимности)
$A=D$ (условие симметрии)

Параметры A , B , C и D линии различаются в зависимости от того, как желаемая модель обрабатывает сопротивление ( R ), индуктивность ( L ), емкость ( C ) и шунтирующую (параллельную, утечку) проводимость G . Четыре основные модели — это аппроксимация короткой линии, аппроксимация средней линии, аппроксимация длинной линии (с распределенными параметрами) и линия без потерь. Во всех описанных моделях заглавная буква, например R, относится к общему количеству, суммированному по линии, а строчная буква, например, r, относится к количеству на единицу длины.

Классификация линий электропередачи переменного тока

Обзор классификации

Линия передачи переменного тока имеет сопротивление R, индуктивность L, емкость C и шунтирующую проводимость или проводимость утечки G. Эти параметры вместе с нагрузкой и линией передачи определяют производительность линии. Термин «производительность» означает конечное напряжение отправки, отправкуконечные токи, конечный коэффициент отправки, потери мощности в линии, эффективность линии передачи, регулирование и ограничение потока мощности во время эффективности и передачи, регулирование и пределы мощности в установившемся и переходном режиме. Линия передачи переменного токаобычно делятся на три класса ^[28]

Короткая линия электропередачи (длина линии ≤ 60 км)
Средняя линия электропередачи (80 км ≤ длина линии ≤ 250 км)
Длинная линия электропередачи (длина линии ≥ 250 км)

Классификация линии электропередачи зависит от частоты передачи мощности и является допущением, сделанным для удобства расчета параметров работы линии и ее потерь. ^[29] И поэтому диапазон длин для категоризации линии передачи не является жестким. Диапазоны длин могут различаться (немного), и все они справедливы в своих областях аппроксимации.

Основа классификации

Вывод напряжения\длины тока тока

Ток и напряжение распространяются в линии передачи со скоростью, равной скорости света (c), т.е. ок. $3\times 10^{8}m/sec=3\times 10^{5}km/sec$ а частота (f) напряжения или тока составляет 50 Гц (хотя в Америке и некоторых частях Азии она обычно составляет 60 Гц) ^[30]

Следовательно, длину волны (λ) можно рассчитать следующим образом:

$f\lambda =c$

или, $\lambda ={\frac {c}{f}}$

или, $\lambda ={\frac {3\times 10^{5}}{50}}=6000Km$

Причина классификации

Линия электропередачи длиной 60 км очень-очень маленькая( ${\tfrac {1}{100}}$ раз) по сравнению с длиной волны, т.е. 6000 км. До 240 км ( ${\tfrac {1}{25}}$ раз длины волны) (для удобства запоминания взято 250 км) Длина линии, форма волны тока или напряжения настолько мала, что для всех практических целей ее можно аппроксимировать прямой линией. Для длины линии около 240 км параметры считаются сосредоточенными (хотя практически эти параметры всегда распределены). Следовательно, характеристику линии передачи на длине до 250 км можно считать линейной и, следовательно, эквивалентную схему линии можно аппроксимировать линейной схемой. Но если длина линии более 250 км, скажем 400 км, т.е. ${\tfrac {1}{15}}$ раз длины волны, то форму волны тока или напряжения нельзя считать линейной, и поэтому нам необходимо использовать интегрирование для анализа этих линий.

Для линий длиной до 60 км это настолько коротко, что влияние параметров шунта практически незаметно на всем протяжении линии. И, следовательно, эти линейные линии относятся к категории коротких линий передачи .
Для линий эффективной длины от 60 до 250 км нельзя пренебрегать влиянием параметров шунта. И, следовательно, они считаются сосредоточенными либо в середине линии (номинальное Т -представление), либо на двух концах линии (номинальное П- представление). Эти линейные линии относятся к категории средних линий передачи.
Для линий электропередачи эффективной длиной более 250 км схему замещения нельзя считать линейной. Параметры распределены, и для анализа производительности необходимы строгие расчеты. Эти нелинейные линии относятся к категории длинных линий передачи .

Короткая линия передачи

Векторная диаграмма короткой линии передачи

Линии электропередачи длиной менее 60 км обычно называют короткими линиями электропередачи. Из-за небольшой длины такие параметры, как электрическое сопротивление, полное сопротивление и индуктивность этих коротких линий, считаются сосредоточенными. Шунтирующая емкость для короткой линии практически незначительна и поэтому не учитывается (или принимается равной нулю).

Вывод значений параметра ABCD

Теперь, если импеданс на км для 1 км линии равен: $z_{0}=r+jx$ и напряжение на передающем и принимающем концах составляет угол $\Phi _{s}$ & $\Phi _{r}$ соответственно, с током принимающего конца. Тогда полное сопротивление линии будет равно: $Z=lr+ljx$

Посылающее конечное напряжение и ток для этого приближения определяются по формуле:

V_{S}=V_{R}+ZI_{R}

( 1 )

I_{S}=I_{R}

( 2 )

При этом напряжения на передающей и принимающей сторонах обозначаются $V_{S}$ и $V_{R}$ соответственно. А еще течения $I_{S}$ и $I_{R}$ входят и выходят из сети соответственно.

Итак, рассматривая модель эквивалентной схемы для короткой линии передачи, матрицу передачи можно получить следующим образом:

{\begin{bmatrix}V_{\mathrm {S} }\\I_{\mathrm {S} }\\\end{bmatrix}}={\begin{bmatrix}1&Z\\0&1\\\end{bmatrix}}{\begin{bmatrix}V_{\mathrm {R} }\\I_{\mathrm {R} }\\\end{bmatrix}}

( 3 )

Следовательно, параметры ABCD имеют вид:

A = D =1, B = Z Ω и C = 0

Средняя линия передачи

Линию электропередачи, имеющая эффективную длину более 80 км, но менее 250 км, обычно называют средней линией электропередачи. Из-за того, что длина линии значительно велика, шунтирующая емкость вместе с адмиттансом Y сети действительно играет роль в расчете эффективных параметров схемы, в отличие от коротких линий передачи. По этой причине моделирование линии передачи средней длины выполняется с использованием сосредоточенной проводимости шунта и сосредоточенного импеданса последовательно с цепью.

Противологичное поведение линий электропередачи средней длины:

повышение напряжения при отсутствии нагрузки или при малом токе ( эффект Ферранти )
ток принимающей стороны может превышать ток отправляющей стороны

Эти сосредоточенные параметры линии электропередачи средней длины можно представить с помощью двух разных моделей, а именно:

Номинальное представление Π

В случае номинального представления Π общая сосредоточенная проводимость шунта делится на две равные половины, и каждая половина со значением Y ⁄ 2 размещается как на передающем, так и на приемном конце, в то время как весь импеданс цепи сосредоточен между двумя половинами. . Сформированная таким образом схема напоминает символ числа пи (Π), поэтому она известна как номинальное Π (или сетевое представление Π) средней линии передачи. В основном он используется для определения общих параметров схемы и выполнения анализа распределения нагрузки.

Вывод значений параметра ABCD

Применяя KCL к двум концам шунта, получаем

$I_{S}=I_{1}+I_{2}={\frac {Y}{2}}V_{S}+{\frac {Y}{2}}V_{R}+I_{R}$

В этом,

Напряжения на передающей и принимающей сторонах обозначаются $V_{S}$ и $V_{R}$ соответственно. А еще течения $I_{S}$ и $I_{R}$ входят и выходят из сети соответственно.

$I_{1}\&I_{3}$ — токи через шунтирующие емкости на передающем и приемном концах соответственно, тогда как $I_{2}$ - ток через последовательное сопротивление.

Снова,

$V_{S}=ZI_{2}+V_{R}=Z(V_{R}{\frac {Y}{2}}+I_{R})+V_{R}$

или,

V_{S}=(1+{\frac {YZ}{2}})V_{R}+ZI_{R}

( 4 )

Итак, подставив, получим:

$I_{S}={\frac {Y}{2}}[(1+{\frac {YZ}{2}})V_{R}+ZI_{R}]+{\frac {Y}{2}}V_{R}+I_{R}$

или,

I_{S}=Y(1+{\frac {YZ}{4}})V_{R}+(1+{\frac {YZ}{2}})I_{R}

( 5 )

Полученное таким образом уравнение eq( 4 ) и ( 5 ) можно записать в матричной форме следующим образом:

{\begin{bmatrix}V_{S}\\I_{S}\\\end{bmatrix}}={\begin{bmatrix}1+{\frac {YZ}{2}}&Z\\Y(1+{\frac {YZ}{4}})&1+{\frac {YZ}{2}}\end{bmatrix}}{\begin{bmatrix}V_{R}\\I_{R}\\\end{bmatrix}}

( 6 )

Итак, параметры ABCD:

А = Д = $(1+{\frac {YZ}{2}})$ за единицу

В = Z Ом

С = $Y(1+{\frac {YZ}{4}})\mho$

Номинальное представление Т

Средняя линия передачи (T-представление)

В номинальной Т-модели линии передачи средней мощности суммарный последовательный импеданс разделен на две половины и расположен по обе стороны от сосредоточенного шунта, т. е. посередине. Сформированная таким образом цепь напоминает символ заглавной буквы T или звезды (Y) и, следовательно, известна как номинальная сеть T линии передачи средней длины.

получение значений параметра ABCD

Применение KCL в месте соединения (нейтральная точка для соединения Y) дает:

$V_{J}={\frac {V_{S}-V_{J}}{\frac {Z}{2}}}=YV_{J}+{\frac {V_{J}-V_{R}}{\frac {Z}{2}}}$

Приведенное выше уравнение можно переписать так:

$V_{J}={\frac {2}{YZ+4}}(V_{S}+V_{R})$

Здесь напряжения на передающей и принимающей сторонах обозначаются $V_{S}$ и $V_{R}$ соответственно. А еще течения $I_{S}$ и $I_{R}$ входят и выходят из сети соответственно

Теперь для тока принимающей стороны мы можем написать:

I_{R}={\frac {V_{J}-V_{R}}{\frac {Z}{2}}}

( 7 )

Переставив уравнение и заменив значение $V_{J}$ с полученным значением мы получаем:

V_{S}=(1+{\frac {YZ}{2}})V_{R}+Z(1+{\frac {YZ}{4}})I_{R}

( 8 )

Теперь конечный ток отправки можно записать как:

$I_{S}=YV_{J}+I_{R}$

Замена значения $V_{J}$ в приведенном выше уравнении:

I_{S}=YV_{R}+(1+{\frac {YZ}{2}})I_{R}

( 9 )

Полученное таким образом уравнение ( 8 ) и уравнение ( 9 ) можно записать в матричной форме следующим образом:

{\begin{bmatrix}V_{S}\\I_{S}\\\end{bmatrix}}={\begin{bmatrix}1+{\frac {YZ}{2}}&Z(1+{\frac {YZ}{4}})\\Y&1+{\frac {YZ}{2}}\end{bmatrix}}{\begin{bmatrix}V_{R}\\I_{R}\\\end{bmatrix}}

( 10 )

Итак, параметры ABCD:

А = Д = $(1+{\frac {YZ}{2}})$ за единицу

Б = $Z(1+{\frac {YZ}{4}})\Omega$

С = $Y\mho$

Длинная линия передачи

Линия электропередачи длиной более 250 км считается длинной линией электропередачи. В отличие от коротких и средних линий параметры длинной линии передачи предполагается распределенными в каждой точке линии равномерно. Таким образом, моделирование длинной линии является несколько затруднительным. Но можно сделать несколько подходов на основе длины и значений параметров линии. Для длинной линии передачи считается, что линия может быть разделена на различные секции, и каждая секция состоит из индуктивности, емкости, сопротивления и проводимости, как показано в каскадной модели RLC (последовательное сопротивление и индуктивность с шунтирующей емкостью). .

Вывод значений параметра ABCD

Подход каскадной модели

Рассмотрим немного меньшую часть длинной линии передачи длиной dx, расположенную на расстоянии x от приемного конца. Последовательное сопротивление линии обозначается как zdx, а ydx — шунтирующее сопротивление линии. Из-за зарядного тока и потерь на корону ток неравномерен по всей линии. Напряжение также различно в разных частях линии из-за индуктивного реактивного сопротивления.

Где,

z – последовательное сопротивление на единицу длины, на фазу

y – проводимость шунта на единицу длины, на фазу к нейтрали

$\Delta V=Iz\Delta x\Rightarrow {\frac {\Delta V}{\Delta x}}=Iz$

Опять же, как $\Delta x\rightarrow 0$

${\frac {\Delta V}{\Delta x}}=Iz$

Теперь для тока через полоску, применив KCL получим,

\Delta I=(V+\Delta V)y\Delta x=Vy\Delta x+y\Delta x\Delta V

( 11 )

Второй член приведенного выше уравнения представляет собой произведение двух малых величин, поэтому им можно пренебречь.

Для $\Delta x\rightarrow 0$ у нас есть, ${\frac {dI}{dx}}=Vy$

Взяв производную по x обеих частей, получим

{\frac {d}{dx}}({\frac {dV}{dx}})=Z{\frac {dI}{dx}}

( 12 )

Замена в приведенном выше уравнении приводит к

{\frac {d^{2}V}{dx^{2}}}-yzV=0

( 13 )

Корни приведенного выше уравнения расположены в точках $\pm {\sqrt {yz}}$ .

Следовательно, решение имеет вид

V={A_{1}e^{x{\sqrt {yz}}}}+{A_{2}e^{-x{\sqrt {yz}}}}

( 14 )

Взяв производную по x, получим:

{\frac {dV}{dx}}={A_{1}{\sqrt {yz}}e^{x{\sqrt {yz}}}}+{A_{2}{\sqrt {yz}}e^{-x{\sqrt {yz}}}}

( 15 )

Объединив эти два, мы имеем:

I={\frac {1}{z}}{\frac {dV}{dx}}={{\frac {A_{1}}{\sqrt {\frac {z}{y}}}}{e^{x{\sqrt {yz}}}}}+{{\frac {A_{2}}{\sqrt {\frac {z}{y}}}}{e^{-x{\sqrt {yz}}}}}

( 16 )

Следующие две величины определяются как:

$Z_{c}={\sqrt {\frac {z}{y}}}$ , который называется характеристическим сопротивлением

$\gamma ={\sqrt {yz}}$ , которая называется постоянной распространения

Тогда предыдущие уравнения можно записать через характеристический импеданс и постоянную распространения как:

V=A_{1}e^{\gamma x}\quad +\quad A_{2}e^{-\gamma x}

( 17 )

I={\frac {A_{1}}{Z_{c}}}e^{\gamma x}\quad +\quad {\frac {A_{2}}{Z_{c}}}e^{-\gamma x}

( 18 )

Теперь, в $x=0$ у нас есть, $V=V_{r}$ и $I=I_{r}$

Поэтому, поставив $x=0$ в уравнении ( 17 ) и уравнении ( 18 ) мы получаем:

V_{r}=A_{1}\quad +\quad A_{2}

( 19 )

I_{r}={\frac {A_{1}}{Z_{c}}}\quad +\quad {\frac {A_{2}}{Z_{c}}}

( 20 )

Решая уравнения ( 19 ) и уравнения ( 20 ), мы получаем следующие значения для $A_{1}\&A_{2}$ :

A_{1}={\frac {V_{r}+Z_{c}I_{r}}{2}}\&A_{2}={\frac {V_{r}+Z_{c}I_{r}}{2}}

( 21 )

Кроме того, для $l=x$ , у нас есть $V=V_{S}$ и $I=I_{S}$ .

Следовательно, заменив x на l, получим:

V_{s}={\frac {V_{r}+Z_{c}I_{r}}{2}}e^{\gamma l}\quad +\quad {\frac {V_{r}-Z_{c}I_{r}}{2}}e^{-\gamma l}

( 22 )

I_{s}={\frac {{\frac {V_{r}}{Z_{c}}}+I_{r}}{2}}e^{\gamma l}\quad +\quad {\frac {{\frac {V_{r}}{Z_{c}}}-I_{r}}{2}}e^{-\gamma l}

( 23 )

Где,

${\frac {V_{r}+Z_{c}I_{r}}{2}}e^{\gamma l}$ называется падающей волной напряжения

${\frac {V_{r}-Z_{c}I_{r}}{2}}e^{-\gamma l}$ называется отраженной волной напряжения

Мы можем переписать уравнения ( 22 ) и уравнения ( 23 ) как:

V_{s}=V_{r}\cosh(\gamma l)+Z_{c}I_{r}\sinh(\gamma l)

( 24 )

I_{s}={\frac {V_{r}}{Z_{c}}}\sinh(\gamma l)+I_{r}\cosh(\gamma l)

( 25 )

Итак, рассматривая соответствующую аналогию для длинной линии передачи, полученные уравнения, т.е. уравнение ( 24 ) и уравнение ( 25 ), можно записать в матричную форму следующим образом:

{\begin{bmatrix}V_{\mathrm {S} }\\I_{\mathrm {S} }\\\end{bmatrix}}={\begin{bmatrix}\cosh \gamma l&Z_{c}\sinh \gamma l\\{\frac {1}{Z_{c}}}\sinh \gamma l&\cosh \gamma l\end{bmatrix}}{\begin{bmatrix}V_{\mathrm {R} }\\I_{\mathrm {R} }\\\end{bmatrix}}

( 26 )

Параметры ABCD задаются следующим образом:

А = Д = $\cosh \gamma l$

Б = $Z_{c}\sinh \gamma l$

С = ${\frac {\sinh \gamma l}{Z_{c}}}$

Π Подход к представлению

Как и средняя линия передачи, длинная линия также может быть аппроксимирована эквивалентным П- представлением. В Π-эквиваленте длинной линии передачи последовательный импеданс обозначается Z', а шунтирующий адмиттанс обозначается Y'.

Таким образом, параметры ABCD этой длинной линии можно определить, как среднюю линию передачи, как:

А = Д = $(1+{\frac {Y\prime Z\prime }{2}})$ за единицу

Б = Z' Ом

С = $Y(1+{\frac {Y\prime Z\prime }{4}})\mho$

Сравнивая его с параметрами ABCD модели каскадной длинной передачи, мы можем написать:

$Z\prime =Z_{C}\sinh \gamma l={\sqrt[{}]{\frac {z}{y}}}\sinh \gamma l=zl{\frac {\sinh \gamma l}{l{\sqrt[{}]{yz}}}}$

или, $Z\prime =Z{\frac {\sinh \gamma l}{\gamma l}}\Omega$

Где Z(= zl) — полное сопротивление линии.

$\cosh \gamma l=1+{\frac {Y\prime Z\prime }{2}}={\frac {Y\prime }{2}}Z_{C}\sinh \gamma l+1$

Переставив приведенное выше уравнение,

${\frac {Y\prime }{2}}={\frac {1}{Z_{C}}}{\frac {\cosh \gamma l-1}{\sinh \gamma l}}$

или, ${\frac {Y\prime }{2}}={\frac {1}{Z_{C}}}\tanh({\frac {\gamma l}{2}})={\sqrt[{}]{\frac {y}{z}}}\tanh({\frac {\gamma l}{2}})$

Это можно свести к следующему:

${\frac {Y\prime }{2}}={\frac {yl}{2}}{\frac {\tanh({\frac {\gamma l}{2}})}{{\frac {l}{2}}{\sqrt[{}]{yz}}}}={\frac {Y}{2}}{\frac {\tanh({\frac {\gamma l}{2}})}{{\frac {(\gamma l}{2}})}}$

где Y(= yl) называется полной проводимостью линии.

Теперь, если длина строки (l) мала, $\sinh \gamma l\equiv \gamma l\quad \&\quad \tanh({\frac {\gamma l}{2}})\equiv {\frac {\gamma l}{2}}$ .

Теперь, если длина линии (l) мала, обнаруживается, что Z = Z' и Y = Y'.

Это означает, что если длина линии (l) мала, может подойти представление номинального π, включающее предположение о сосредоточенных параметрах. Но если длина линии (l) превышает определенную границу (около 240–250), представление номинального π становится ошибочным и не может быть использовано в дальнейшем для анализа производительности. ^[31]

Бегущие волны

Бегущие волны — это волны тока и напряжения, которые создают помехи и движутся по линии передачи от передающего конца линии передачи к другому концу с постоянной скоростью. Бегущая волна играет важную роль в определении напряжений и токов во всех точках энергосистемы. Эти волны также помогают при проектировании изоляторов, защитного оборудования, изоляции оконечного оборудования и общей координации изоляции.

Когда переключатель замкнут на начальном конце линии передачи, напряжение на другом конце не появится мгновенно. Это вызвано переходным поведением катушек индуктивности и конденсаторов, присутствующих в линии передачи. Линии передачи могут не иметь физических индукторов и конденсаторных элементов, но в линии существуют эффекты индуктивности и емкости. Следовательно, когда переключатель замкнут, напряжение на линейных проводниках будет постепенно нарастать. Это явление обычно называется тем, что волна напряжения распространяется от передающего конца линии передачи к другому концу. Аналогично происходит постепенная зарядка емкостей за счет сопутствующей волны тока.

Если в любой момент времени переключатель замкнут, напряжение на нагрузке появляется не мгновенно. Сначала заряжается первая секция, а затем заряжается следующая секция. До тех пор, пока какой-либо раздел не будет заряжен, последующий раздел не будет взиматься плата. Таким образом, этот процесс является постепенным. Это может быть реализовано таким образом, что несколько резервуаров для воды расположены соединенно, и вода течет из 1-го резервуара в последний резервуар.

См. также

Ссылки

^ Синглтон, Пол (1 июля 2002 г.). «Моделирование производительности — что, почему, когда и как». Технологический журнал BT . 20 (3): 133–143. дои : 10.1023/А:1020860029447 . ISSN 1573-1995 . S2CID 60839185 .
^ Стивен В. Фардо и Дейл Р. Патрик, Технология электроэнергетических систем, третье издание , Taylor & Francisco Ltd., США, 2008 г., ISBN 978-1-4398-0027-0 , Глава 8. Основы распределения электроэнергии.
^ Электроэнергетические системы . Уиди, Б.М. (Биррон Мэтью) (5-е изд.). Чичестер, Западный Суссекс, Великобритания: John Wiley & Sons, Ltd., 2012. с. 319. ИСБН 9780470682685 . OCLC 789661388 . {{cite book}}: CS1 maint: другие ( ссылка )
^ Падияр, КР (1990). Системы передачи электроэнергии HVDC: технологии и системное взаимодействие . Нью-Йорк: Уайли. п. 21. ISBN 0470217065 . OCLC 22388689 .
^ Перейти обратно: ^а ^б Мехта, В.К., 1944- (2005). Принципы энергосистемы: (включая генерацию, передачу, распределение, распределительное устройство и защиту) . Мехта, Рохит (писатель по электротехнике) (4-е изд.). Нью-Дели: С. Чанд. п. 126. ИСБН 8121924960 . OCLC 61139348 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )
^ Перейти обратно: ^а ^б Мехта, В.К., 1944- (2005). Принципы энергосистемы: (включая генерацию, передачу, распределение, распределительное устройство и защиту) . Мехта, Рохит (писатель по электротехнике) (4-е изд.). Нью-Дели: С. Чанд. п. 159. ИСБН 8121924960 . OCLC 61139348 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )
^ Перейти обратно: ^а ^б Мехта, В.К., 1944- (2005). Принципы энергосистемы: (включая генерацию, передачу, распределение, распределительное устройство и защиту) . Мехта, Рохит (писатель по электротехнике) (4-е изд.). Нью-Дели: С. Чанд. п. 264. ИСБН 8121924960 . OCLC 61139348 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )
^ Эль-Хавари, Мэн (1995). Электроэнергетические системы: проектирование и анализ (Печатное издание). Нью-Йорк: Институт инженеров по электротехнике и электронике. п. 92. ИСБН 9780470544464 . OCLC 557445432 .
^ Дж. Ф. Уилсон, Ферранти и британская электротехническая промышленность, 1864–1930, Manchester University Press, 1988 ISBN 0-7190-2369-6 стр. 44
^ Прерывание зарядного тока линии с помощью автоматических выключателей высокого и сверхвысокого напряжения, Карл-Эйнар Сёльвер, доктор философии и Сержио де А. Мораис, магистр наук. Архивировано 26 января 2007 г. в Wayback Machine.
^ База знаний по коммутации перенапряжений, А.И. Ибрагим и Х.В. Доммель. Архивировано 12 мая 2006 г., в Wayback Machine.
^ Учебник электротехники, Тераджа, ISBN 978-81-219-2440-5 , SChand & Co.
^ Форбс Т. Браун (2006). Динамика инженерных систем . ЦРК Пресс. п. 43. ИСБН 978-0-8493-9648-9 .
^ Кеннет Л. Кайзер (2004). Справочник по электромагнитной совместимости . ЦРК Пресс. стр. 13–52. ISBN 978-0-8493-2087-3 .
^ «Краткая история электромагнетизма» (PDF) .
^ CL Wadhwa, Electrical Power Systems, седьмое многоцветное издание , New Age International (P) Limited, Нью-Дели, 2017 г., ISBN 978-93-86070-19-7 , Глава 2. Расчеты констант линии.
^ «Определение фарада » . Коллинз.
^ Уильям Д. Грисон (1992). Электростатический разряд в электронике . Пресса научных исследований. п. 48. ИСБН 978-0-86380-136-5 . Проверено 4 декабря 2011 г.
^ CL Wadhwa, Electrical Power Systems, седьмое многоцветное издание , New Age International (P) Limited, Нью-Дели, 2017 г., ISBN 978-93-86070-19-7 , Глава 3 Емкость линий электропередачи
^ Ушида, Джун; Токусима, Масатоши; Ширане, Масаюки; Гомё, Акико; Ямада, Хирохито (2003). «Согласование иммитанса многомерных фотонных кристаллов открытой системы». Физический обзор B . 68 (15): 155115. arXiv : cond-mat/0306260 . Бибкод : 2003PhRvB..68o5115U . дои : 10.1103/PhysRevB.68.155115 . S2CID 119500762 .
^ Дж. Гловер, М. Сарма и Т. Овербай, Анализ и проектирование энергосистем, пятое издание , Cengage Learning, Коннектикут, 2012 г., ISBN 978-1-111-42577-7 , Глава 5 Линии передачи: установившаяся работа
^ Грей, §3.2, с. 172
^ Джагер, §10.5 §13.5 §13.8
^ Электроэнергетические системы: проектирование и анализ, Мэриленд Э.Эль-Хавари, ISBN 0-7803-1140X , стр. 157.
^ Гош, стр.353.
^ А. Чакрабарти, стр.581, ISBN 81-7700-000-4 , Dhanpat Rai & Co pvt. ООО
^ А. Чакрабарти, ISBN 81-7700-000-4 , Dhanpat Rai & Co pvt. ООО
^ Курсы NPTEL. Глава 2: Модели линий электропередачи ( https://nptel.ac.in/courses/117104071/chap2.pdf )
^ CL Wadhwa, Electrical Power Systems, седьмое многоцветное издание , New Age International (P) Limited, Нью-Дели, 2017 г., ISBN 978-93-86070-19-7 , Глава 2. Характеристики линий.
^ AC Monteith, CF Wagner (редактор), Справочник по передаче и распределению электроэнергии, 4-е издание , Westinghouse Electric Corporation, 1950, стр. 6
^ CL Wadhwa, стр. 62, ISBN 978-93-86070-19-7 , New Age International Pvt. ООО

Дальнейшее чтение

Григсби, LL и др. Справочник по электроэнергетике . США: CRC Press. (2001). ISBN 0-8493-8578-4
Физика повседневных вещей — линии электропередачи

[1] Синглтон, Пол (1 июля 2002 г.). «Моделирование производительности — что, почему, когда и как». Технологический журнал BT . 20 (3): 133–143. дои : 10.1023/А:1020860029447 . ISSN 1573-1995 . S2CID 60839185 .

[2] Стивен В. Фардо и Дейл Р. Патрик, Технология электроэнергетических систем, третье издание , Taylor & Francisco Ltd., США, 2008 г., ISBN 978-1-4398-0027-0 , Глава 8. Основы распределения электроэнергии.

[3] Электроэнергетические системы . Уиди, Б.М. (Биррон Мэтью) (5-е изд.). Чичестер, Западный Суссекс, Великобритания: John Wiley & Sons, Ltd., 2012. с. 319. ИСБН 9780470682685 . OCLC 789661388 . {{cite book}}: CS1 maint: другие ( ссылка )

[4] Падияр, КР (1990). Системы передачи электроэнергии HVDC: технологии и системное взаимодействие . Нью-Йорк: Уайли. п. 21. ISBN 0470217065 . OCLC 22388689 .

[:0-5] Перейти обратно: ^а ^б Мехта, В.К., 1944- (2005). Принципы энергосистемы: (включая генерацию, передачу, распределение, распределительное устройство и защиту) . Мехта, Рохит (писатель по электротехнике) (4-е изд.). Нью-Дели: С. Чанд. п. 126. ИСБН 8121924960 . OCLC 61139348 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )

[:1-6] Перейти обратно: ^а ^б Мехта, В.К., 1944- (2005). Принципы энергосистемы: (включая генерацию, передачу, распределение, распределительное устройство и защиту) . Мехта, Рохит (писатель по электротехнике) (4-е изд.). Нью-Дели: С. Чанд. п. 159. ИСБН 8121924960 . OCLC 61139348 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )

[:2-7] Перейти обратно: ^а ^б Мехта, В.К., 1944- (2005). Принципы энергосистемы: (включая генерацию, передачу, распределение, распределительное устройство и защиту) . Мехта, Рохит (писатель по электротехнике) (4-е изд.). Нью-Дели: С. Чанд. п. 264. ИСБН 8121924960 . OCLC 61139348 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )

[8] Эль-Хавари, Мэн (1995). Электроэнергетические системы: проектирование и анализ (Печатное издание). Нью-Йорк: Институт инженеров по электротехнике и электронике. п. 92. ИСБН 9780470544464 . OCLC 557445432 .

[9] Дж. Ф. Уилсон, Ферранти и британская электротехническая промышленность, 1864–1930, Manchester University Press, 1988 ISBN 0-7190-2369-6 стр. 44

[10] Прерывание зарядного тока линии с помощью автоматических выключателей высокого и сверхвысокого напряжения, Карл-Эйнар Сёльвер, доктор философии и Сержио де А. Мораис, магистр наук. Архивировано 26 января 2007 г. в Wayback Machine.

[11] База знаний по коммутации перенапряжений, А.И. Ибрагим и Х.В. Доммель. Архивировано 12 мая 2006 г., в Wayback Machine.

[12] Учебник электротехники, Тераджа, ISBN 978-81-219-2440-5 , SChand & Co.

[brown-13] Форбс Т. Браун (2006). Динамика инженерных систем . ЦРК Пресс. п. 43. ИСБН 978-0-8493-9648-9 .

[kaiser-14] Кеннет Л. Кайзер (2004). Справочник по электромагнитной совместимости . ЦРК Пресс. стр. 13–52. ISBN 978-0-8493-2087-3 .

[15] «Краткая история электромагнетизма» (PDF) .

[16] CL Wadhwa, Electrical Power Systems, седьмое многоцветное издание , New Age International (P) Limited, Нью-Дели, 2017 г., ISBN 978-93-86070-19-7 , Глава 2. Расчеты констант линии.

[17] «Определение фарада » . Коллинз.

[18] Уильям Д. Грисон (1992). Электростатический разряд в электронике . Пресса научных исследований. п. 48. ИСБН 978-0-86380-136-5 . Проверено 4 декабря 2011 г.

[19] CL Wadhwa, Electrical Power Systems, седьмое многоцветное издание , New Age International (P) Limited, Нью-Дели, 2017 г., ISBN 978-93-86070-19-7 , Глава 3 Емкость линий электропередачи

[20] Ушида, Джун; Токусима, Масатоши; Ширане, Масаюки; Гомё, Акико; Ямада, Хирохито (2003). «Согласование иммитанса многомерных фотонных кристаллов открытой системы». Физический обзор B . 68 (15): 155115. arXiv : cond-mat/0306260 . Бибкод : 2003PhRvB..68o5115U . дои : 10.1103/PhysRevB.68.155115 . S2CID 119500762 .

[21] Дж. Гловер, М. Сарма и Т. Овербай, Анализ и проектирование энергосистем, пятое издание , Cengage Learning, Коннектикут, 2012 г., ISBN 978-1-111-42577-7 , Глава 5 Линии передачи: установившаяся работа

[Gray-22] Грей, §3.2, с. 172

[Jaeger-23] Джагер, §10.5 §13.5 §13.8

[24] Электроэнергетические системы: проектирование и анализ, Мэриленд Э.Эль-Хавари, ISBN 0-7803-1140X , стр. 157.

[25] Гош, стр.353.

[26] А. Чакрабарти, стр.581, ISBN 81-7700-000-4 , Dhanpat Rai & Co pvt. ООО

[27] А. Чакрабарти, ISBN 81-7700-000-4 , Dhanpat Rai & Co pvt. ООО

[28] Курсы NPTEL. Глава 2: Модели линий электропередачи ( https://nptel.ac.in/courses/117104071/chap2.pdf )

[29] CL Wadhwa, Electrical Power Systems, седьмое многоцветное издание , New Age International (P) Limited, Нью-Дели, 2017 г., ISBN 978-93-86070-19-7 , Глава 2. Характеристики линий.

[30] AC Monteith, CF Wagner (редактор), Справочник по передаче и распределению электроэнергии, 4-е издание , Westinghouse Electric Corporation, 1950, стр. 6

[31] CL Wadhwa, стр. 62, ISBN 978-93-86070-19-7 , New Age International Pvt. ООО

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]