Радиус

В геометрии радиус классической ( мн.ч .: радиусы или радиусы ) ^[а] круга — это любой или сферы из отрезков линии от его центра до периметра , а в более современном использовании — это также их длина. Название происходит от латинского радиуса , что означает луч, а также от спицы колеса колесницы. ^[2] Типичное сокращение и математической переменной имя для радиуса — R или r . В более широком смысле диаметр D определяется как двойной радиус: ^[3]

d\doteq 2r\quad \Rightarrow \quad r={\frac {d}{2}}.

Если у объекта нет центра, этот термин может относиться к его радиусу или описанной окружности описанной сфере . В любом случае радиус может быть больше половины диаметра, который обычно определяется как максимальное расстояние между любыми двумя точками фигуры. Внутренний радиус геометрической фигуры обычно равен радиусу наибольшего круга или сферы, содержащейся в ней. Внутренний радиус кольца, трубки или другого полого предмета — это радиус его полости.

Для правильных многоугольников радиус равен радиусу описанной окружности. ^[4] Внутренний радиус правильного многоугольника также называют апофемой . В теории графов радиус графа — это минимальное по всем вершинам u максимальное расстояние от u до любой другой вершины графа. ^[5]

Радиус круга с периметром ( окружностью ) C равен

r={\frac {C}{2\pi }}

Формула

Для многих геометрических фигур радиус имеет четко определенную связь с другими мерами фигуры.

Круги

Радиус круга площадью $А$ равен

r={\sqrt {\frac {A}{\pi }}}.

Радиус окружности, проходящей через неколлинеарные точки $P1 три$ , $P2,$ и $P3 выражением$ определяется

r={\frac {|{\vec {OP_{1}}}-{\vec {OP_{3}}}|}{2\sin \theta }},

где $θ$ — угол $∠ P 1 P 2 P 3$ . Эта формула использует закон синусов . Если три точки заданы своими координатами $(x 1, y 1)$ , $(x 2, y 2)$ и $(x 3, y 3)$ , радиус можно выразить как

r={\frac {\sqrt {{\bigl (}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}{\bigr )}{\bigl (}(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}{\bigr )}{\bigl (}(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}{\bigr )}}}{2{\bigl |}x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}{\bigr |}}}.

Правильные многоугольники

$н$	$Р н$
3	0.577 350...
4	0.707 106...
5	0.850 650...
6	1.0
7	1.152 382...
8	1.306 562...
9	1.461 902...
10	1.618 033...

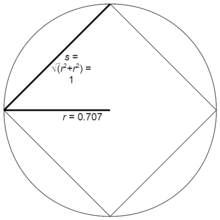
Радиус $r$ правильного многоугольника с $n$ сторонами длины $s$ определяется выражением $r = R n s$ , где $R_{n}=1\left/\left(2\sin {\frac {\pi }{n}}\right)\right..$ Значения $R n$ для малых значений $n$ приведены в таблице. Если $s = 1$ , то эти значения также являются радиусами соответствующих правильных многоугольников.

Гиперкубы

Радиус d -мерного гиперкуба со стороной s равен

r={\frac {s}{2}}{\sqrt {d}}.

Использование в системах координат

Полярные координаты

Полярная система координат — это система координат в , которой каждая точка плоскости двумерная определяется расстоянием от фиксированной точки и углом от фиксированного направления.

Неподвижная точка (аналог начала декартовой системы ) называется полюсом , а луч от полюса в фиксированном направлении — полярной осью . Расстояние от полюса называется радиальной координатой или радиусом , а угол — угловой координатой , полярным углом или азимутом . ^[6]

Цилиндрические координаты

В цилиндрической системе координат есть выбранная базовая ось и выбранная базовая плоскость, перпендикулярная этой оси. Началом . системы является точка, в которой все три координаты могут быть заданы как ноль Это пересечение базовой плоскости и оси.

Ось по-разному называют цилиндрической или продольной осью, чтобы отличить ее отполярная ось , представляющая собой луч , лежащий в базовой плоскости, начиная с начала координат и указывая в опорном направлении.

Расстояние от оси можно назвать радиальным расстоянием или радиусом . в то время как угловую координату иногда называют угловым положением или азимутом .Радиус и азимут вместе называются полярными координатами , поскольку они соответствуют двумерной полярной системе координат в плоскости, проходящей через точку, параллельную базовой плоскости.Третью координату можно назвать высотой или высотой (если плоскость отсчета считать горизонтальной). продольное положение , ^[7] или осевое положение . ^[8]

Сферические координаты

В сферической системе координат радиус описывает расстояние точки от фиксированного начала координат. Его положение, если оно дополнительно определяется полярным углом, измеренным между радиальным направлением и фиксированным направлением зенита, и углом азимута, углом между ортогональной проекцией радиального направления на опорную плоскость, которая проходит через начало координат и ортогональна зениту. и фиксированное опорное направление в этой плоскости.

См. также

Примечания

^ Радиус во множественном числе может быть либо радиусами (от латинского множественного числа), либо обычными английскими радиусами множественного числа . ^[1]

Ссылки

^ «Радиус — определение и многое другое из бесплатного словаря Merriam-Webster» . Merriam-webster.com . Проверено 22 мая 2012 г.
^ Определение радиуса на словаре.reference.com. Доступ осуществлен 8 августа 2009 г.
^ Определение радиуса на mathwords.com. Доступ осуществлен 8 августа 2009 г.
^ Барнетт Рич, Кристофер Томас (2008), Очерк геометрии Шаума , 4-е издание, 326 страниц. МакГроу-Хилл Профессионал. ISBN 0-07-154412-7 , ISBN 978-0-07-154412-2 . Доступ к онлайн-версии состоялся 8 августа 2009 г.
^ Джонатан Л. Гросс, Джей Йеллен (2006), Теория графов и ее приложения . 2-е издание, 779 страниц; ЦРК Пресс. ISBN 1-58488-505-X , 9781584885054. Доступ к онлайн-версии осуществлен 8 августа 2009 г.
^ Браун, Ричард Г. (1997). Эндрю М. Глисон (ред.). Высшая математика: предварительное исчисление с дискретной математикой и анализом данных . Эванстон, Иллинойс: Макдугал Литтел. ISBN 0-395-77114-5 .
^ Крафт, К.; Волокитин А.С. (1 января 2002 г.). «Резонансное взаимодействие электронного пучка с несколькими низшими гибридными волнами» . Физика плазмы . 9 (6): 2786–2797. Бибкод : 2002PhPl....9.2786K . дои : 10.1063/1.1465420 . ISSN 1089-7674 . Архивировано из оригинала 14 апреля 2013 года . Проверено 9 февраля 2013 г. ...в цилиндрических координатах ( r , θ , z ) ... и Z=v _bz t — продольное положение...
^ Гройсман, Александр; Стейнберг, Виктор (24 февраля 1997 г.). «Пары одиночных вихрей в вязкоупругом течении Куэтта». Письма о физических отзывах . 78 (8). Американское физическое общество (APS): 1460–1463. arXiv : patt-sol/9610008 . Бибкод : 1997PhRvL..78.1460G . дои : 10.1103/physrevlett.78.1460 . ISSN 0031-9007 . S2CID 54814721 . «[...]где r , θ и z - цилиндрические координаты [...] как функция осевого положения [...]»

[2] Радиус во множественном числе может быть либо радиусами (от латинского множественного числа), либо обычными английскими радиусами множественного числа . ^[1]

[1] «Радиус — определение и многое другое из бесплатного словаря Merriam-Webster» . Merriam-webster.com . Проверено 22 мая 2012 г.

[radic-3] Определение радиуса на словаре.reference.com. Доступ осуществлен 8 августа 2009 г.

[mwd1-4] Определение радиуса на mathwords.com. Доступ осуществлен 8 августа 2009 г.

[schaum-5] Барнетт Рич, Кристофер Томас (2008), Очерк геометрии Шаума , 4-е издание, 326 страниц. МакГроу-Хилл Профессионал. ISBN 0-07-154412-7 , ISBN 978-0-07-154412-2 . Доступ к онлайн-версии состоялся 8 августа 2009 г.

[yel-6] Джонатан Л. Гросс, Джей Йеллен (2006), Теория графов и ее приложения . 2-е издание, 779 страниц; ЦРК Пресс. ISBN 1-58488-505-X , 9781584885054. Доступ к онлайн-версии осуществлен 8 августа 2009 г.

[brown-7] Браун, Ричард Г. (1997). Эндрю М. Глисон (ред.). Высшая математика: предварительное исчисление с дискретной математикой и анализом данных . Эванстон, Иллинойс: Макдугал Литтел. ISBN 0-395-77114-5 .

[8] Крафт, К.; Волокитин А.С. (1 января 2002 г.). «Резонансное взаимодействие электронного пучка с несколькими низшими гибридными волнами» . Физика плазмы . 9 (6): 2786–2797. Бибкод : 2002PhPl....9.2786K . дои : 10.1063/1.1465420 . ISSN 1089-7674 . Архивировано из оригинала 14 апреля 2013 года . Проверено 9 февраля 2013 г. ...в цилиндрических координатах ( r , θ , z ) ... и Z=v _bz t — продольное положение...

[9] Гройсман, Александр; Стейнберг, Виктор (24 февраля 1997 г.). «Пары одиночных вихрей в вязкоупругом течении Куэтта». Письма о физических отзывах . 78 (8). Американское физическое общество (APS): 1460–1463. arXiv : patt-sol/9610008 . Бибкод : 1997PhRvL..78.1460G . дои : 10.1103/physrevlett.78.1460 . ISSN 0031-9007 . S2CID 54814721 . «[...]где r , θ и z - цилиндрические координаты [...] как функция осевого положения [...]»

[а]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[1]