Модель с сосредоточенными параметрами сердечно-сосудистой системы

Пример сердечно-сосудистой модели с сосредоточенными параметрами. Каждое отделение находится внутри зеленых коробок. Параметры модели выделены черным цветом, а синим — артериальное давление и потоки крови во всей сердечно-сосудистой системе.

Модель сердечно-сосудистой системы с сосредоточенными параметрами представляет собой нульмерную математическую модель, используемую для описания гемодинамики сердечно -сосудистой системы . Учитывая набор параметров, имеющих физический смысл (например, сопротивление току крови), он позволяет изучать изменения артериального давления или скорости кровотока во всей сердечно-сосудистой системе. ^[1]^[2] Модифицируя параметры, можно изучить последствия конкретного заболевания . Например, артериальная гипертензия моделируется увеличением артериального сопротивления модели. ^[1]

Модель с сосредоточенными параметрами используется для изучения гемодинамики трехмерного пространства (сердечно-сосудистой системы) с помощью нульмерного пространства, использующего аналогию между трубами и электрическими цепями. Сокращение измерений от трех до нуля осуществляется путем разделения сердечно-сосудистой системы на различные отделы. , каждый из них представляет определенный компонент системы, например правое предсердие или системные артерии. Каждый отсек состоит из простых схемных компонентов, таких как сопротивления или конденсаторы , при этом поток крови ведет себя как ток, текущий через цепь в соответствии с законами Кирхгофа , под действием кровяного давления (падения напряжения). ^[2]

Модель с сосредоточенными параметрами представляет собой систему обыкновенных дифференциальных уравнений , описывающую эволюцию во времени объемов камер сердца. , а также кровяное давление и потоки через кровеносные сосуды . ^[3]

Описание модели

Модель с сосредоточенными параметрами представляет собой систему обыкновенных дифференциальных уравнений, которые придерживаются принципов сохранения массы и импульса . Модель получена с использованием электрической аналогии, где ток представляет собой поток крови, напряжение представляет собой разность давлений, электрическое сопротивление играет роль сосудистого сопротивления (определяется сечением и длиной кровеносного сосуда), емкость играет роль роль сосудистой податливости (способность сосуда расширяться и увеличивать объем при увеличении трансмурального давления , то есть разницы давлений между двумя сторонами стенки сосуда) и индуктивности представляет собой инерцию крови . Каждая камера сердца моделируется с помощью эластансов , которые описывают сократимость сердечной мышцы и разгруженный объем, то есть объем крови, содержащейся в камере при нулевом давлении. Лампы виде выполнены в диодов . Параметрами модели являются сопротивления, емкости, индуктивности и упругости. Неизвестными для системы являются объемы крови внутри каждой камеры сердца, кровяное давление и потоки крови внутри каждого отдела кровообращения. Система обыкновенных дифференциальных уравнений решается с помощью численного метода временной дискретизации , например метода Рунге-Кутты . ^[3]

Сердечно-сосудистая система разделена на несколько отделов:

четыре камеры сердца: левое и правое предсердия, левый и правый желудочки;
большой круг кровообращения, который можно разделить на артерии, вены и, при необходимости, на другие отделы с учетом различных кровеносных сосудов;
малый круг кровообращения, который можно разделить на артерии, вены и, при необходимости, на другие отделы, учитывающие различные кровеносные сосуды.

Ниже левого предсердия и желудочка и правого предсердия и желудочка расположены четыре сердечных клапана: митральный , аортальный , трикуспидальный и легочный клапаны соответственно. ^[3]

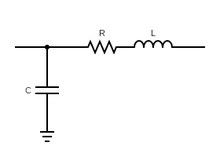
Разделение малого и большого круга кровообращения не фиксировано, например, если интерес исследования представляют системные капилляры, в модель с сосредоточенными параметрами можно добавить отсек, учитывающий системные капилляры. Каждый отсек описывается схемой Виндкесселя с количеством элементов, зависящим от конкретного отсека. Обыкновенные дифференциальные уравнения модели получены на основе схем Виндкесселя и законов Кирхгофа. ^[4]

В дальнейшем основное внимание будет уделено конкретной модели с сосредоточенными параметрами. Рассматриваются четыре камеры сердца, системные и легочные артерии и вены. ^[5]

Уравнения камер сердца

Параметры, относящиеся к четырем камерам сердца, — это пассивная и активная эластичность. $EA_{XX}$ и $EB_{XX}$ (где индексы различаются в зависимости от $RA,RV,LA$ и $LV$ если эластичность относится к правому предсердию или желудочку или левому предсердию или желудочку соответственно) и ненагруженным объемам $V0_{XX}$ . Динамика камер сердца описывается зависящей от времени эластичностью: ^[5]

E_{XX}(t)=EB_{XX}+EA_{XX}f_{XX}(t)

где $f_{XX}(t)$ представляет собой периодическую (с периодом сердцебиения) зависящую от времени функцию в пределах от $0$ к $1$ это объясняет фазы активации сердца во время сердцебиения. Из приведенного выше уравнения пассивная эластичность представляет собой минимальную эластичность камеры сердца, тогда как сумма $EA_{XX}$ и $EB_{XX}$ его максимальная эластичность. Зависящая от времени эластичность позволяет рассчитать давление внутри конкретной камеры сердца следующим образом: ^[5]

p_{XX}(t)=E_{XX}(t)(V_{XX}(t)-V0_{XX})

где $V_{XX}(t)$ - объем крови, содержащейся в камере сердца, а объемы каждой камеры являются решениями следующих обыкновенных дифференциальных уравнений, которые учитывают входящие и внешние потоки крови, связанные с камерой сердца: ^[5]

{\frac {dV_{LA}(t)}{dt}}=Q_{VEN}^{PUL}(t)-Q_{MV}(t)

{\frac {dV_{LV}(t)}{dt}}=Q_{MV}(t)-Q_{AV}(t)

{\frac {dV_{RA}(t)}{dt}}=Q_{VEN}^{SYS}(t)-Q_{TV}(t)

{\frac {dV_{RV}(t)}{dt}}=Q_{TV}(t)-Q_{PV}(t)

где $Q_{MV}(t),Q_{AV}(t),Q_{TV}(t)$ и $Q_{PV}(t)$ – потоки через митральный, аортальный, трикуспидальный и легочный клапаны соответственно и $Q_{VEN}^{PUL}(t)$ и $Q_{VEN}^{SYS}(t)$ – потоки через легочные и системные вены соответственно. ^[5]

Уравнения клапанов

Клапаны моделируются как диоды, и потоки крови через клапаны зависят от скачков давления между входным и выходным отсеками: ^[5]

Q_{MV}(t)=Q_{valve}(p_{LA}(t)-p_{LV}(t))\qquad Q_{AV}(t)=Q_{valve}(p_{LV}(t)-p_{AR}^{SYS}(t))

Q_{TV}(t)=Q_{valve}(p_{RA}(t)-p_{RV}(t))\qquad Q_{TV}(t)=Q_{valve}(p_{RV}(t)-p_{AR}^{PUL}(t))

где давление внутри каждой камеры сердца определено в предыдущем разделе, $p_{AR}^{SYS}(t)$ и $p_{AR}^{PUL}(t)$ - зависящее от времени давление внутри системного и легочного артерий и $Q_{valve}(\Delta p)$ – поток через клапан в зависимости от скачка давления: ^[5]

Q_{valve}(\Delta p)={\begin{cases}{\frac {\Delta p}{R_{min}}}\qquad &{\text{if }}\Delta p<0\\{\frac {\Delta p}{R_{max}}}\qquad &{\text{if }}\Delta p\geq 0\end{cases}}

где $R_{min}$ и $R_{max}$ – сопротивления клапанов, когда они открыты и закрыты соответственно. ^[5]

Уравнения циркуляционных отсеков

Каждый отсек кровеносных сосудов характеризуется сочетанием сопротивлений, емкостей и индуктивностей. Например, артериальный большой круг кровообращения можно описать тремя параметрами: $R_{AR}^{SYS},C_{AR}^{SYS}$ и $L_{AR}^{SYS}$ которые представляют артериальное системное сопротивление, емкость и индуктивность. Обыкновенные дифференциальные уравнения, описывающие системное артериальное кровообращение: ^[5]

C_{AR}^{SYS}{\frac {dp_{AR}^{SYS}}{dt}}=Q_{AV}(t)-Q_{AR}^{SYS}(t)

L_{AR}^{SYS}{\frac {dQ_{AR}^{SYS}(t)}{dt}}=-R_{AR}^{SYS}Q_{AR}^{SYS}(t)+p_{AR}^{SYS}(t)-p_{VEN}^{SYS}(t)

где $Q_{AR}^{SYS}(t)$ — кровоток через системный артериальный отдел и $p_{VEN}^{SYS}(t)$ давление внутри венозного отсека. ^[5]

Аналогичные уравнения с аналогичными обозначениями справедливы и для остальных отделов, описывающих кровообращение. ^[5]

Система обыкновенных дифференциальных уравнений

Собирая описанные выше уравнения, получаем следующую систему: $\forall \,t\in [0,T]$ оно держится ^[5]

{\begin{cases}{\frac {dV_{LA}(t)}{dt}}=Q_{VEN}^{PUL}(t)-Q_{MV}(t)\\{\frac {dV_{LV}(t)}{dt}}=Q_{MV}(t)-Q_{AV}(t)\\C_{AR}^{SYS}{\frac {dp_{AR}^{SYS}(t)}{dt}}=Q_{AV}(t)-Q_{AR}^{SYS}(t)\\L_{AR}^{SYS}{\frac {dQ_{AR}^{SYS}(t)}{dt}}=-R_{AR}^{SYS}Q_{AR}^{SYS}(t)+p_{AR}^{SYS}(t)-p_{VEN}^{SYS}(t)\\C_{VEN}^{SYS}{\frac {dp_{VEN}^{SYS}(t)}{dt}}=Q_{AR}^{SYS}(t)-Q_{VEN}^{SYS}(t)\\L_{VEN}^{SYS}{\frac {dQ_{VEN}^{SYS}(t)}{dt}}=-R_{VEN}^{SYS}Q_{VEN}^{SYS}(t)+p_{VEN}^{SYS}(t)-p_{RA}(t)\\{\frac {dV_{RA}(t)}{dt}}=Q_{VEN}^{SYS}(t)-Q_{TV}(t)\\{\frac {dV_{RV}(t)}{dt}}=Q_{TV}(t)-Q_{PV}(t)\\C_{AR}^{PUL}{\frac {dp_{AR}^{PUL}(t)}{dt}}=Q_{PV}(t)-Q_{AR}^{PUL}(t)\\L_{AR}^{PUL}{\frac {dQ_{AR}^{PUL}(t)}{dt}}=-R_{AR}^{PUL}Q_{AR}^{PUL}(t)+p_{AR}^{PUL}(t)-p_{VEN}^{PUL}(t)\\C_{VEN}^{PUL}{\frac {dp_{VEN}^{PUL}(t)}{dt}}=Q_{AR}^{PUL}(t)-Q_{VEN}^{PUL}(t)\\L_{VEN}^{PUL}{\frac {dQ_{VEN}^{PUL}(t)}{dt}}=-R_{VEN}^{PUL}Q_{VEN}^{PUL}(t)+p_{VEN}^{PUL}(t)-p_{LA}(t)\end{cases}}

Результаты сердечно-сосудистой модели с сосредоточенными параметрами: давление, объемы крови внутри камер сердца и потоки крови.

с $T$ последний раз. Первые два уравнения связаны с объемами левого предсердия и желудочков соответственно. Уравнения с третьего по шестое связаны с давлением и потоками системной артериальной и венозной систем. Аналогичным образом последние уравнения связаны с правыми отделами сердца и малым кругом кровообращения. Система дополняется начальными условиями для каждого из неизвестных. ^[5]

С математической точки зрения корректность задачи является следствием теоремы Коши–Липшица , поэтому ее решение существует и оно единственно. Решение системы аппроксимируется численным методом . Численное моделирование должно быть рассчитано более чем на $10$ сердцебиение (последний раз $T$ зависит от числа сердечных сокращений и частоты сердечных сокращений ) для приближения к предельному циклу динамической системы , так что решение ведет себя аналогично периодической функции, имитирующей периодичность сердечного цикла . ^[5]

Дальнейшие разработки

Описанная выше модель представляет собой конкретную модель с сосредоточенными параметрами. Его можно легко модифицировать, добавляя или удаляя отсеки или компоненты схемы внутри любого отсека по мере необходимости. Уравнения, которые управляют новыми или модифицированными отсеками, по-прежнему являются законами Кирхгофа. ^[4]

Модели с сосредоточенными параметрами сердечно-сосудистой системы можно усовершенствовать, добавив модель с сосредоточенными параметрами для дыхательной системы. Что касается сердечно-сосудистой системы, то дыхательная система разделена на различные отсеки, моделирующие, например, гортань , глотку или трахею . ^[6] Более того, кардиопульмональную модель можно комбинировать с моделью оксигенации крови для изучения, например, уровней насыщения крови. ^[7]^[8]

Существует несколько моделей с сосредоточенными параметрами, и выбор модели зависит от цели работы или исследования. Сложные модели могут описывать разную динамику, но рост сложности влечет за собой увеличение вычислительных затрат на решение системы дифференциальных уравнений. ^[9]^[10]^[11]

Некоторые из 0-D отсеков модели с сосредоточенными параметрами можно заменить на $d$ -мерные компоненты ( $d=1,2,3$ ) для геометрического описания конкретного компонента сердечно-сосудистой системы (например, 0-D отсек левого желудочка можно заменить его трехмерным представлением). Как следствие, система уравнений будет включать также уравнения в частных производных для описания размерных компонентов, и это повлечет за собой большие вычислительные затраты для численного решения. ^[12]^[13]

См. также

Ссылки

^ Jump up to: ^а ^б Шим, Ын Бо; Сах, Чон Юб; Юн, Чан Хён (2004). «Математическое моделирование динамики сердечно-сосудистой системы с использованием метода сосредоточенных параметров» . Японский журнал физиологии . 54 (6): 545–553. дои : 10.2170/jjphysicalol.54.545 . ISSN 0021-521X . ПМИД 15760487 .
^ Jump up to: ^а ^б Ши, Юбинг; Лоуфорд, Патрисия; Хоуз, Родни (2011). «Обзор нулевой и одномерной моделей кровотока в сердечно-сосудистой системе» . Биомедицинская инженерия онлайн . 10 (1): 33. дои : 10.1186/1475-925X-10-33 . ISSN 1475-925Х . ПМК 3103466 . ПМИД 21521508 .
^ Jump up to: ^а ^б ^с Шим, Ын Бо; Сах, Чон Юб; Юн, Чан Хён (2004). «Математическое моделирование динамики сердечно-сосудистой системы с использованием метода сосредоточенных параметров» . Японский журнал физиологии . 54 (6): 545–553. дои : 10.2170/jjphysicalol.54.545 . ISSN 0021-521X . ПМИД 15760487 .
^ Jump up to: ^а ^б Ши, Юбинг; Лоуфорд, Патрисия; Хоуз, Родни (2011). «Обзор нулевой и одномерной моделей кровотока в сердечно-сосудистой системе» . Биомедицинская инженерия онлайн . 10 (1): 33. дои : 10.1186/1475-925X-10-33 . ISSN 1475-925Х . ПМК 3103466 . ПМИД 21521508 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н Деде, Лука; Регаццони, Франческо; Вергара, Кристиан; Зунино, Паоло; Уильям, Марк; Скрофани, Роберто; Фузини, Лаура; Коглиати, Кьяра; Понтоне, Джанлука; Квартерони, Альфио (2021). «Моделирование реакции сердца на гемодинамические изменения, связанные с COVID-19: вычислительное исследование» . Математические биологические науки и инженерия . 18 (4): 3364–3383. дои : 10.3934/mbe.2021168 . hdl : 2434/843779 . ISSN 1551-0018 . ПМИД 34198390 . S2CID 234973850 .
^ Нго, Чуонг; Дальманс, Стефан; Воллмер, Томас; Мисгельд, Берно; Леонхардт, Штеффен (01 июня 2018 г.). «Объектно-ориентированная вычислительная модель для изучения сердечно-легочных гемодинамических взаимодействий у человека» . Компьютерные методы и программы в биомедицине . 159 : 167–183. дои : 10.1016/j.cmpb.2018.03.008 . ISSN 0169-2607 . ПМИД 29650311 . S2CID 4802953 .
^ Альбанезе, Антонио; Ченг, Лимей; Урсино, Мауро; Чбат, Николас В. (01 апреля 2016 г.). «Интегрированная математическая модель сердечно-легочной системы человека: разработка модели» . Американский журнал физиологии. Физиология сердца и кровообращения . 310 (7): H899–H921. дои : 10.1152/ajpheart.00230.2014 . ISSN 0363-6135 . ПМИД 26683899 .
^ Лу, К.; Кларк, Дж.В.; Горбель, Ф.Х.; Уэр, ДЛ; Бидани, А. (1 декабря 2001 г.). «Модель сердечно-легочной системы человека, примененная к анализу маневра Вальсальвы» . Американский журнал физиологии. Физиология сердца и кровообращения . 281 (6): H2661–H2679. дои : 10.1152/ajpheart.2001.281.6.H2661 . ISSN 0363-6135 . ПМИД 11709436 . S2CID 8246967 .
^ Де Лаззари, К.; Даровский, М.; Феррари, Г.; Пизанелли, DM; Тости, Г. (2006). «Моделирование при исследовании взаимодействия аппарата гемонасоса и искусственной вентиляции легких» . Компьютеры в биологии и медицине . 36 (11): 1235–1251. doi : 10.1016/j.compbiomed.2005.08.001 . ПМИД 16202402 .
^ Ши, Юбинг; Коракианитис, Феодосий (2006). «Численное моделирование сердечно-сосудистой динамики при левожелудочковой недостаточности и последовательном вспомогательном устройстве для пульсации желудочков» . Искусственные органы . 30 (12): 929–948. дои : 10.1111/j.1525-1594.2006.00326.x . ISSN 0160-564X . ПМИД 17181834 .
^ Хельдт, Томас; Шим, Ын Б.; Камм, Роджер Д.; Марк, Роджер Г. (1 марта 2002 г.). «Вычислительное моделирование сердечно-сосудистой реакции на ортостатический стресс» . Журнал прикладной физиологии . 92 (3): 1239–1254. doi : 10.1152/japplphysicalol.00241.2001 . ISSN 8750-7587 . ПМИД 11842064 .
^ Бланко, Пабло Дж.; Фейхоо, Рауль А. (2010). «Вычислительная модель 3D-1D-0D для всей сердечно-сосудистой системы» . Вычислительная механика . 29 (59): 5887–5911.
^ Байаржон, Брайан; Ребело, Нуно; Фокс, Дэвид Д.; Тейлор, Роберт Л.; Куль, Эллен (2014). «Проект «Живое сердце»: надежный и интегрированный симулятор работы сердца человека» . Европейский журнал механики – A/Solids . 48 : 38–47. Бибкод : 2014EuJMA..48...38B . doi : 10.1016/j.eurotechsol.2014.04.001 . ПМЦ 4175454 . PMID 25267880 .

Дальнейшее чтение

Базилевс, Юрий; Такидзава, Кендзи; Тездуяр, Тайфун Э. (2013). Вычисление взаимодействия жидкости и конструкции: методы и приложения . Ряды Вили по вычислительной механике. Чичестер: Уайли. ISBN 978-0-470-97877-1 .
Квартерони, Альфио ; Деде, Лука; Манцони, Андреа; Вергара, Кристиан (2019). Математическое моделирование сердечно-сосудистой системы человека: данные, численная аппроксимация, клиническое применение . Кембриджские монографии по прикладной и вычислительной математике. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. ISBN 978-1-108-61609-6 .
Хиршфогель, Марк; Бассилиус, Марина; Джагшис, Лассе; Уайлдхирт, Стивен М.; Ну и дела, Майкл В. (2017). «Монолитная 3D-0D-связанная модель сердца и сосудистой системы с замкнутым контуром: экспериментальная оценка параметров сердечной механики для конкретного пациента: 3D-0D-связанная модель сердца с замкнутым контуром» . Международный журнал численных методов в биомедицинской инженерии . 33 (8): e2842. дои : 10.1002/cnm.2842 . ПМИД 27743468 . S2CID 36252500 .

[:3-1] Jump up to: ^а ^б Шим, Ын Бо; Сах, Чон Юб; Юн, Чан Хён (2004). «Математическое моделирование динамики сердечно-сосудистой системы с использованием метода сосредоточенных параметров» . Японский журнал физиологии . 54 (6): 545–553. дои : 10.2170/jjphysicalol.54.545 . ISSN 0021-521X . ПМИД 15760487 .

[:4-2] Jump up to: ^а ^б Ши, Юбинг; Лоуфорд, Патрисия; Хоуз, Родни (2011). «Обзор нулевой и одномерной моделей кровотока в сердечно-сосудистой системе» . Биомедицинская инженерия онлайн . 10 (1): 33. дои : 10.1186/1475-925X-10-33 . ISSN 1475-925Х . ПМК 3103466 . ПМИД 21521508 .

[:2-3] Jump up to: ^а ^б ^с Шим, Ын Бо; Сах, Чон Юб; Юн, Чан Хён (2004). «Математическое моделирование динамики сердечно-сосудистой системы с использованием метода сосредоточенных параметров» . Японский журнал физиологии . 54 (6): 545–553. дои : 10.2170/jjphysicalol.54.545 . ISSN 0021-521X . ПМИД 15760487 .

[:1-4] Jump up to: ^а ^б Ши, Юбинг; Лоуфорд, Патрисия; Хоуз, Родни (2011). «Обзор нулевой и одномерной моделей кровотока в сердечно-сосудистой системе» . Биомедицинская инженерия онлайн . 10 (1): 33. дои : 10.1186/1475-925X-10-33 . ISSN 1475-925Х . ПМК 3103466 . ПМИД 21521508 .

[:0-5] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н Деде, Лука; Регаццони, Франческо; Вергара, Кристиан; Зунино, Паоло; Уильям, Марк; Скрофани, Роберто; Фузини, Лаура; Коглиати, Кьяра; Понтоне, Джанлука; Квартерони, Альфио (2021). «Моделирование реакции сердца на гемодинамические изменения, связанные с COVID-19: вычислительное исследование» . Математические биологические науки и инженерия . 18 (4): 3364–3383. дои : 10.3934/mbe.2021168 . hdl : 2434/843779 . ISSN 1551-0018 . ПМИД 34198390 . S2CID 234973850 .

[6] Нго, Чуонг; Дальманс, Стефан; Воллмер, Томас; Мисгельд, Берно; Леонхардт, Штеффен (01 июня 2018 г.). «Объектно-ориентированная вычислительная модель для изучения сердечно-легочных гемодинамических взаимодействий у человека» . Компьютерные методы и программы в биомедицине . 159 : 167–183. дои : 10.1016/j.cmpb.2018.03.008 . ISSN 0169-2607 . ПМИД 29650311 . S2CID 4802953 .

[7] Альбанезе, Антонио; Ченг, Лимей; Урсино, Мауро; Чбат, Николас В. (01 апреля 2016 г.). «Интегрированная математическая модель сердечно-легочной системы человека: разработка модели» . Американский журнал физиологии. Физиология сердца и кровообращения . 310 (7): H899–H921. дои : 10.1152/ajpheart.00230.2014 . ISSN 0363-6135 . ПМИД 26683899 .

[8] Лу, К.; Кларк, Дж.В.; Горбель, Ф.Х.; Уэр, ДЛ; Бидани, А. (1 декабря 2001 г.). «Модель сердечно-легочной системы человека, примененная к анализу маневра Вальсальвы» . Американский журнал физиологии. Физиология сердца и кровообращения . 281 (6): H2661–H2679. дои : 10.1152/ajpheart.2001.281.6.H2661 . ISSN 0363-6135 . ПМИД 11709436 . S2CID 8246967 .

[hemopump-9] Де Лаззари, К.; Даровский, М.; Феррари, Г.; Пизанелли, DM; Тости, Г. (2006). «Моделирование при исследовании взаимодействия аппарата гемонасоса и искусственной вентиляции легких» . Компьютеры в биологии и медицине . 36 (11): 1235–1251. doi : 10.1016/j.compbiomed.2005.08.001 . ПМИД 16202402 .

[10] Ши, Юбинг; Коракианитис, Феодосий (2006). «Численное моделирование сердечно-сосудистой динамики при левожелудочковой недостаточности и последовательном вспомогательном устройстве для пульсации желудочков» . Искусственные органы . 30 (12): 929–948. дои : 10.1111/j.1525-1594.2006.00326.x . ISSN 0160-564X . ПМИД 17181834 .

[11] Хельдт, Томас; Шим, Ын Б.; Камм, Роджер Д.; Марк, Роджер Г. (1 марта 2002 г.). «Вычислительное моделирование сердечно-сосудистой реакции на ортостатический стресс» . Журнал прикладной физиологии . 92 (3): 1239–1254. doi : 10.1152/japplphysicalol.00241.2001 . ISSN 8750-7587 . ПМИД 11842064 .

[12] Бланко, Пабло Дж.; Фейхоо, Рауль А. (2010). «Вычислительная модель 3D-1D-0D для всей сердечно-сосудистой системы» . Вычислительная механика . 29 (59): 5887–5911.

[13] Байаржон, Брайан; Ребело, Нуно; Фокс, Дэвид Д.; Тейлор, Роберт Л.; Куль, Эллен (2014). «Проект «Живое сердце»: надежный и интегрированный симулятор работы сердца человека» . Европейский журнал механики – A/Solids . 48 : 38–47. Бибкод : 2014EuJMA..48...38B . doi : 10.1016/j.eurotechsol.2014.04.001 . ПМЦ 4175454 . PMID 25267880 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]