Конус (теория категорий)

В теории категорий , разделе математики , конус функтора — это абстрактное понятие, используемое для определения предела этого функтора . Конусы также появляются в теории категорий.

Определение

Пусть F : J → C — диаграмма в C. ​ Формально диаграмма — это не что иное, функтор из J в C. как Изменение терминологии отражает тот факт, что мы думаем о F индексаторе семейства объектов и морфизмов в C. как об Категория . J считается «индексной категорией» Это следует рассматривать по аналогии с понятием индексированного семейства объектов в теории множеств . Основное отличие состоит в том, что здесь мы также имеем морфизмы. Так, например, когда J — дискретная категория , она наиболее близко соответствует идее индексированного семейства в теории множеств. Другой распространенный и более интересный пример предполагает, что J — это диапазон . J также можно считать пустой категорией, что приводит к простейшим конусам.

Пусть N — объект C . Конус из N в — это F семейство морфизмов

$\psi _{X}\colon N\to F(X)\,$

для каждого объекта X из J , такого, что для каждого морфизма f : X → Y в J следующая диаграмма коммутирует :

Part of a cone from N to F

Коллекция (обычно бесконечная) всех этих треугольников может быть (частично) изображена в форме конуса вершиной N. с что конус ψ имеет вершину N и основание F. Иногда говорят ,

Можно также определить двойственное понятие конуса от F до N ( также называемого коконусом ), поменяв местами все стрелки выше. Явно коконус из F в N представляет собой семейство морфизмов

$\psi _{X}\colon F(X)\to N\,$

для каждого объекта X из J , такого, что для каждого морфизма f : X → Y в J коммутирует следующая диаграмма:

Part of a cone from F to N

Эквивалентные

На первый взгляд конусы кажутся несколько ненормальными конструкциями в теории категорий. Это отображения объекта в функтор (или наоборот). В соответствии с духом теории категорий мы хотели бы определить их как морфизмы или объекты некоторой подходящей категории. На самом деле, мы можем сделать и то, и другое.

Пусть J — малая категория и пусть C ^Дж — категория диаграмм типа J в C (это не что иное, как категория функтора ). Определим диагональный функтор Δ : C → C ^Дж следующим образом: Δ( N ) : J → C — постоянный функтор N всех для N в C .

Если F — диаграмма типа J в C , следующие утверждения эквивалентны:

• ψ — конус из N в F
• ψ — естественное преобразование из ∆( N ) в F
• ( N , ψ) — объект в категории запятой (Δ ↓ F )

Двойные утверждения также эквивалентны:

• ψ — коконус из F в N
• ψ — естественное преобразование из F в Δ( N )
• ( N , ψ) — объект в категории запятой ( F ↓ Δ)

Все эти утверждения можно проверить путем непосредственного применения определений. Думая о конусах как о естественных преобразованиях, мы видим, что это всего лишь морфизмы в C. ^Дж с источником (или целью) постоянным функтором.

Категория конусов

Исходя из вышесказанного, мы можем определить категорию конусов F как категорию запятой (Δ ↓ F ). Морфизмы конусов тогда являются просто морфизмами этой категории. Эта эквивалентность коренится в наблюдении, что естественное отображение между постоянными функторами Δ( N ), Δ( M ) соответствует морфизму между N и M . В этом смысле диагональный функтор тривиально действует на стрелки. Аналогично, запись определения естественного отображения постоянного функтора Δ( N ) в F дает ту же диаграмму, что и выше. Как и следовало ожидать, морфизм конуса ( N , ψ) в конус ( L , φ) — это просто морфизм N → L такой, что все «очевидные» диаграммы коммутируют (см. первую диаграмму в следующем разделе).

Аналогично, категория коконусов из F является категорией запятой ( F ↓ Δ).

Универсальные конусы

Пределы и копределы определяются как универсальные конусы . То есть конусы, через которые действуют все остальные конусы. Конус φ из L в F называется универсальным конусом, если для любого другого конуса ψ из N в F существует единственный морфизм из ψ в φ.

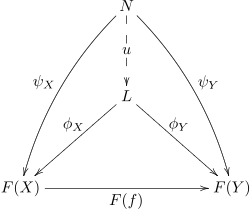
Эквивалентно, универсальный конус в F — это универсальный морфизм из Δ в F (думаемый как объект в C ^Дж ) или терминальный объект в (Δ ↓ F ).

Двойственным образом конус φ из F в L является универсальным конусом, если для любого другого конуса ψ из F в N существует единственный морфизм из φ в ψ.

Эквивалентно, универсальный конус из F является универсальным морфизмом из F в Δ или исходным объектом в ( F ↓ Δ).

Предел F — универсальный конус из F , а копредел — универсальный конус F. из Как и во всех универсальных конструкциях, существование универсальных конусов не гарантируется для всех диаграмм F , но если они существуют, то они уникальны с точностью до единственного изоморфизма (в категории запятой (Δ ↓ F )).

См. также

• Обратный предел # Конусы - Конструкция в теории категорий

Ссылки

• Мак Лейн, Сондерс (1998). Категории для работающего математика (2-е изд.). Нью-Йорк: Спрингер. ISBN  0-387-98403-8 .
• Борсо, Фрэнсис (1994). «Пределы». Справочник по категориальной алгебре . Энциклопедия математики и ее приложений 50-51, 53 [т.е. 52]. Том. 1. Издательство Кембриджского университета. ISBN  0-521-44178-1 .

Внешние ссылки

• Конус в n лаборатории