Метод переназначения

Метод переназначения — это метод улучшения частотно-временного представления (например, спектрограммы или кратковременного преобразования Фурье ) путем сопоставления данных с частотно-временными координатами, которые ближе к истинной области поддержки анализируемого сигнала. Этот метод был независимо представлен несколькими сторонами под разными названиями, включая метод переназначения , переназначения , переназначения частоты времени и модифицированного метода скользящего окна . ^[1] Метод переназначения повышает четкость размытых частотно-временных данных путем перемещения данных в соответствии с локальными оценками мгновенной частоты и групповой задержки. Такое сопоставление с переназначенными частотно-временными координатами является очень точным для сигналов, которые можно разделить по времени и частоте относительно окна анализа.

Введение

Многие сигналы, представляющие интерес, имеют распределение энергии, которое меняется во времени и частоте. Например, любой звуковой сигнал, имеющий начало или конец, имеет распределение энергии, которое меняется во времени, и большинство звуков демонстрируют значительные изменения как во времени, так и по частоте в течение своей продолжительности. Частотно-временные представления обычно используются для анализа или характеристики таких сигналов. Они отображают одномерный сигнал во временной области в двумерную функцию времени и частоты. Частотно-временное представление описывает изменение спектрального распределения энергии во времени, так же, как музыкальная партитура описывает изменение музыкальной высоты во времени.

При анализе аудиосигнала спектрограмма является наиболее часто используемым частотно-временным представлением, вероятно, потому, что она хорошо понятна и невосприимчива к так называемым «перекрестным терминам», которые иногда затрудняют интерпретацию других частотно-временных представлений. Но операция оконной обработки, необходимая при вычислении спектрограммы, приводит к неприятному компромиссу между временным и частотным разрешением, поэтому спектрограммы обеспечивают частотно-временное представление, размытое во времени, частоте или в обоих измерениях. Метод частотно-временного переназначения представляет собой метод перефокусировки частотно-временных данных в размытом представлении, таком как спектрограмма, путем сопоставления данных с частотно-временными координатами, которые ближе к истинной области поддержки анализируемого сигнала. ^[2]

Спектрограмма как частотно-временное представление

Одним из наиболее известных частотно-временных представлений является спектрограмма, определяемая как квадрат величины кратковременного преобразования Фурье. Хотя известно, что кратковременный фазовый спектр содержит важную временную информацию о сигнале, эту информацию трудно интерпретировать, поэтому обычно при кратковременном спектральном анализе рассматривается только кратковременный спектр амплитуды. ^[2]

Как представление частоты времени, спектрограмма имеет относительно низкое разрешение. Разрешение по времени и частоте определяется выбором окна анализа, и большая концентрация в одной области сопровождается большим размытием в другой. ^[2]

Частотно-временное представление, имеющее улучшенное разрешение по сравнению со спектрограммой, представляет собой распределение Вигнера-Вилля , которое можно интерпретировать как кратковременное преобразование Фурье с оконной функцией, которая идеально соответствует сигналу. Распределение Вигнера-Вилля сильно сконцентрировано по времени и частоте, но оно также сильно нелинейно и нелокально. Следовательно, этоРаспределение очень чувствительно к шуму и генерирует перекрестные компоненты, которые часто маскируют интересующие компоненты, что затрудняет извлечение полезной информации, касающейся распределения энергии в многокомпонентных сигналах. ^[2]

Класс билинейных частотно-временных представлений Коэна представляет собой класс «сглаженных» распределений Вигнера – Вилля, в которых используется сглаживающее ядро, которое может снизить чувствительность распределения к шуму и подавлять перекрестные компоненты за счет размытия распределения по времени и частоте. . Это размытие приводит к тому, что распределение становится отличным от нуля в областях, где истинное распределение Вигнера – Вилля не показывает энергии. ^[2]

Спектрограмма является членом класса Коэна. Это сглаженное распределение Вигнера-Вилля со сглаживающим ядром, равным распределению Вигнера-Вилля окна анализа. Метод переназначения сглаживает распределение Вигнера-Вилля, но затем перефокусирует распределение обратно на истинные области поддержки компонент сигнала. Было показано, что этот метод сокращает время и частоту размытия любого члена класса Коэна. ^[2]^[3]В случае переназначенияспектрограмма, коротковременной фазовый спектр используется дляисправить номинальные временные и частотные координатыспектральные данные и сопоставить их ближе к истинным областямподдержка анализируемого сигнала.

Метод переназначения

Новаторская работа по методу переназначения была опубликована Кодерой, Гендрином и де Вилледари под названием « Модифицированный метод скользящего окна» . ^[4] Их метод повышает разрешение по времени и частоте классического метода скользящего окна (эквивалентного спектрограмме) путем присвоения каждой точке данных новой частотно-временной координаты, которая лучше отражает распределение энергии в анализируемом сигнале. ^[4]^: 67

В классическом методе скользящего окна сигнал во временной области $x(t)$ разлагается на набор коэффициентов, $\epsilon (t,\omega )$ , основанный на наборе элементарных сигналов, $h_{\omega }(t)$ , определенный ^[4]^: 73

h_{\omega }(t)=h(t)e^{j\omega t}

где $h(t)$ — это (действительная) функция ядра нижних частот, подобная оконной функции в кратковременном преобразовании Фурье. Коэффициенты в этом разложении определены

{\begin{aligned}\epsilon (t,\omega )&=\int x(\tau )h(t-\tau )e^{-j\omega \left[\tau -t\right]}d\tau \\&=e^{j\omega t}\int x(\tau )h(t-\tau )e^{-j\omega \tau }d\tau \\&=e^{j\omega t}X(t,\omega )\\&=X_{t}(\omega )\\&=M_{t}(\omega )e^{j\phi _{\tau }(\omega )}\end{aligned}}

где $M_{t}(\omega )$ это величина, и $\phi _{\tau }(\omega )$ фаза, из $X_{t}(\omega )$ , преобразование Фурье сигнала $x(t)$ сдвинут во времени на $t$ и окном $h(t)$ . ^[5]^: 4

$x(t)$ может быть восстановлен из коэффициентов скользящего окна с помощью ^[5]^: 8

{\begin{aligned}x(t)&=\iint X_{\tau }(\omega )h_{\omega }^{*}(\tau -t)d\omega d\tau \\&=\iint X_{\tau }(\omega )h(\tau -t)e^{-j\omega \left[\tau -t\right]}d\omega d\tau \\&=\iint M_{\tau }(\omega )e^{j\phi _{\tau }(\omega )}h(\tau -t)e^{-j\omega \left[\tau -t\right]}d\omega d\tau \\&=\iint M_{\tau }(\omega )h(\tau -t)e^{j\left[\phi _{\tau }(\omega )-\omega \tau +\omega t\right]}d\omega d\tau \end{aligned}}

Для сигналов, имеющих спектры амплитуд, $M(t,\omega )$ , изменение во времени которого медленно относительно изменения фазы, максимальный вклад в интеграл восстановления вносит окрестность точки $t,\omega$ удовлетворяющее условию стационарности фазы ^[4]^: 74

{\begin{aligned}{\frac {\partial }{\partial \omega }}\left[\phi _{\tau }(\omega )-\omega \tau +\omega t\right]&=0\\{\frac {\partial }{\partial \tau }}\left[\phi _{\tau }(\omega )-\omega \tau +\omega t\right]&=0\end{aligned}}

или, что то же самое, вокруг точки ${\hat {t}},{\hat {\omega }}$ определяется ^[4]^: 74

{\begin{aligned}{\hat {t}}(\tau ,\omega )&=\tau -{\frac {\partial \phi _{\tau }(\omega )}{\partial \omega }}=-{\frac {\partial \phi (\tau ,\omega )}{\partial \omega }}\\{\hat {\omega }}(\tau ,\omega )&={\frac {\partial \phi _{\tau }(\omega )}{\partial \tau }}=\omega +{\frac {\partial \phi (\tau ,\omega )}{\partial \tau }}\end{aligned}}

Это явление известно в таких областях, как оптика, как принцип стационарной фазы , который гласит, что для периодических или квазипериодических сигналов изменение фазового спектра Фурье, не связанное с периодическими колебаниями, медленно по отношению ко времени вблизи точки частота колебаний, а в окружающих регионах изменение относительно быстрое. Аналогично, для импульсных сигналов, сконцентрированных во времени, изменение фазового спектра вблизи момента импульса происходит медленно по частоте, а в окружающих областях изменение относительно быстрое. ^[4]^: 73

При реконструкции положительные и отрицательные вклады в синтезированную форму сигнала компенсируются из-за деструктивной интерференции в частотных областях с быстрым изменением фазы. Только области медленного изменения фазы (стационарная фаза) будут вносить существенный вклад в реконструкцию, а максимальный вклад (центр тяжести) происходит в точке, где фаза меняется наиболее медленно по времени и частоте. ^[4]^: 71

Вычисленные таким образом частотно-временные координаты равны локальной групповой задержке, ${\hat {t}}_{g}(t,\omega ),$ и местная мгновенная частота, ${\hat {\omega }}_{i}(t,\omega ),$ и вычисляются по фазе кратковременного преобразования Фурье, которое обычно игнорируется при построении спектрограммы. Эти величины являются локальными в том смысле, что они представляют собой оконный и отфильтрованный сигнал, локализованный во времени и частоте, и не являются глобальными свойствами анализируемого сигнала. ^[4]^: 70

Метод модифицированного скользящего окна, или метод переназначения, меняет (переназначает) точку отнесения $\epsilon (t,\omega )$ до этой точки максимального вклада ${\hat {t}}(t,\omega ),{\hat {\omega }}(t,\omega )$ , а не по существу $t,\omega$ по которому он рассчитывается. Эту точку иногда называют центром тяжести распределения по аналогии с распределением массы. Эта аналогия является полезным напоминанием о том, что приписывание спектральной энергии центру тяжести ее распределения имеет смысл только тогда, когда есть энергия, которую можно приписать, поэтому метод переназначения не имеет смысла в точках, где спектрограмма имеет нулевое значение. ^[2]

Эффективное вычисление переназначенных времен и частот

При цифровой обработке сигналов чаще всего производится выборка во временной и частотной областях. Дискретное преобразование Фурье используется для вычисления выборок. $X(k)$ преобразования Фурье по выборкам $x(n)$ сигнала во временной области. Операции по переназначению, предложенные Kodera et al. не может быть применен непосредственно к данным дискретного кратковременного преобразования Фурье, поскольку частные производные не могут быть вычислены непосредственно на данных, дискретных по времени и частоте, и было высказано предположение, что эта трудность была основным препятствием для более широкого использования метода. о переназначении.

Частные производные можно аппроксимировать с помощью конечных разностей. Например, фазовый спектр можно оценить в два близлежащих момента времени, а частную производную по времени можно аппроксимировать как разницу между двумя значениями, деленную на разницу во времени, как в

{\begin{aligned}{\frac {\partial \phi (t,\omega )}{\partial t}}&\approx {\frac {1}{\Delta t}}\left[\phi \left(t+{\frac {\Delta t}{2}},\omega \right)-\phi \left(t-{\frac {\Delta t}{2}},\omega \right)\right]\\{\frac {\partial \phi (t,\omega )}{\partial \omega }}&\approx {\frac {1}{\Delta \omega }}\left[\phi \left(t,\omega +{\frac {\Delta \omega }{2}}\right)-\phi \left(t,\omega -{\frac {\Delta \omega }{2}}\right)\right]\end{aligned}}

При достаточно малых значениях $\Delta t$ и $\Delta \omega ,$ и при условии, что разность фаз соответствующим образом «развернута», этот метод конечных разностей дает хорошие аппроксимации частных производных фазы, поскольку в областях спектра, в которых в эволюции фазы преобладает вращение из-за синусоидальных колебаний один, близлежащий компонент, фаза является линейной функцией.

Независимо от Кодеры и др. Нельсон пришел к аналогичному методу улучшения частотно-временной точности кратковременных спектральных данных из частных производных коротковременной фазы.спектр. ^[6] Легко показать, что кросс-спектральные поверхности Нельсона вычисляют аппроксимацию производных, эквивалентную методу конечных разностей.

Огер и Фландрин показали, что метод переназначения, предложенный Кодерой и др. в контексте спектрограммы, может быть распространен на любого члена класса частотно-временных представлений Коэна путем обобщения операций переназначения на

{\begin{aligned}{\hat {t}}(t,\omega )&=t-{\frac {\iint \tau \cdot W_{x}(t-\tau ,\omega -\nu )\cdot \Phi (\tau ,\nu )d\tau d\nu }{\iint W_{x}\left(t-\tau ,\omega -\nu \right)\cdot \Phi (\tau ,\nu )d\tau d\nu }}\\{\hat {\omega }}(t,\omega )&=\omega -{\frac {\iint \nu \cdot W_{x}(t-\tau ,\omega -\nu )\cdot \Phi (\tau ,\nu )d\tau d\nu }{\iint W_{x}(t-\tau ,\omega -\nu )\cdot \Phi (\tau ,\nu )d\tau d\nu }}\end{aligned}}

где $W_{x}(t,\omega )$ представляет собой распределение Вигнера – Вилля $x(t)$ , и $\Phi (t,\omega )$ — это функция ядра, определяющая распределение. Далее они описали эффективный метод эффективного и точного вычисления времени и частоты для переназначенной спектрограммы без явного вычисления частных производныхфаза. ^[2]

В случае спектрограммы операции переназначения можно вычислить с помощью

{\begin{aligned}{\hat {t}}(t,\omega )&=t-\Re \left\{{\frac {X_{{\mathcal {T}}h}(t,\omega )\cdot X^{*}(t,\omega )}{|X(t,\omega )|^{2}}}\right\}\\{\hat {\omega }}(t,\omega )&=\omega +\Im \left\{{\frac {X_{{\mathcal {D}}h}(t,\omega )\cdot X^{*}(t,\omega )}{|X(t,\omega )|^{2}}}\right\}\end{aligned}}

где $X(t,\omega )$ — это кратковременное преобразование Фурье, рассчитанное с использованием окна анализа. $h(t),X_{{\mathcal {T}}h}(t,\omega )$ — это кратковременное преобразование Фурье, рассчитанное с использованием окна анализа, взвешенного по времени. $h_{\mathcal {T}}(t)=t\cdot h(t)$ и $X_{{\mathcal {D}}h}(t,\omega )$ — это кратковременное преобразование Фурье, рассчитанное с использованием окна анализа производной по времени. $h_{\mathcal {D}}(t)={\tfrac {d}{dt}}h(t)$ .

Использование вспомогательных оконных функций $h_{\mathcal {T}}(t)$ и $h_{\mathcal {D}}(t)$ операции переназначения могут быть вычислены в любой частотно-временной координате $t,\omega$ из алгебраической комбинации трех преобразований Фурье, оцененных при $t,\omega$ . Поскольку эти алгоритмы работают только с кратковременными спектральными данными, оцениваемыми в один и тот же момент времени и на одной частоте, и не вычисляют явным образом какие-либо производные, это дает эффективный метод вычисления переназначенного дискретного кратковременного преобразования Фурье.

Одним из ограничений этого метода вычислений является то, что $|X(t,\omega )|^{2}$ должно быть ненулевым. Это не является большим ограничением, поскольку сама операция переназначения подразумевает наличие некоторой энергии для переназначения и не имеет смысла, когда распределение имеет нулевое значение.

Разделимость

Кратковременное преобразование Фурье часто можно использовать для оценки амплитуд и фаз отдельных компонентов многокомпонентного сигнала , такого как квазигармонический тон музыкального инструмента. Более того, операции переназначения времени и частоты могут использоваться для уточнения представления путем приписывания спектральной энергии, сообщаемой кратковременным преобразованием Фурье, точке, которая является локальным центром тяжести сложного распределения энергии. ^[7]

Для сигнала, состоящего из одного компонента, мгновенная частота может быть оценена по частным производным фазы любого канала кратковременного преобразования Фурье, который проходит через компонент. Если сигнал необходимо разложить на множество компонентов,

x(t)=\sum _{n}A_{n}(t)e^{j\theta _{n}(t)}

а мгновенная частота каждой компоненты определяется как производная ее фазы по времени, т.е.

\omega _{n}(t)={\frac {d\theta _{n}(t)}{dt}},

тогда мгновенная частота каждого отдельного компонента может быть вычислена по фазе отклика фильтра, пропускающего этот компонент, при условии, что в полосе пропускания фильтра находится не более одного компонента.

Это свойство в частотной области, которое Нельсон назвал разделимостью. ^[6] и требуется для всех анализируемых таким образом сигналов. Если это свойство не соблюдено, то желаемое многокомпонентное разложение не может быть достигнуто, поскольку параметры отдельных компонентов невозможно оценить из кратковременного преобразования Фурье. В таких случаях необходимо выбрать другое окно анализа, чтобы обеспечить соблюдение критерия разделимости.

Если компоненты сигнала разделены по частоте относительно конкретного окна кратковременного спектрального анализа, то выходной сигнал каждого фильтра кратковременного преобразования Фурье представляет собой отфильтрованную версию, самое большее, одной доминанты (имеющей значительную энергию). компонент и, следовательно, производная по времени фазы $X(t,\omega _{0})$ равна производной по времени фазы доминирующего компонента в точке $\omega _{0}.$ Поэтому, если компонент, $x_{n}(t),$ имеющий мгновенную частоту $\omega _{n}(t)$ является доминирующим компонентом вблизи $\omega _{0},$ тогда мгновенная частота этого компонента может быть вычислена из фазы кратковременного преобразования Фурье, оцененной как $\omega _{0}.$ То есть,

{\begin{aligned}\omega _{n}(t)&={\frac {\partial }{\partial t}}\arg\{x_{n}(t)\}\\&={\frac {\partial }{\partial t}}\arg\{X(t,\omega _{0})\}\end{aligned}}

Так же, как каждый полосовой фильтр в наборе фильтров кратковременного преобразования Фурье может пропускать не более одной комплексной экспоненциальной составляющей, два временных события должны быть достаточно разделены во времени, чтобы они не лежали в одном оконном сегменте входного сигнала. Это свойство разделимости во временной области, и оно эквивалентно требованию, чтобы время между двумя событиями былобольше, чем длина импульсной характеристики фильтров кратковременного преобразования Фурье, диапазон ненулевых отсчетов в $h(t).$

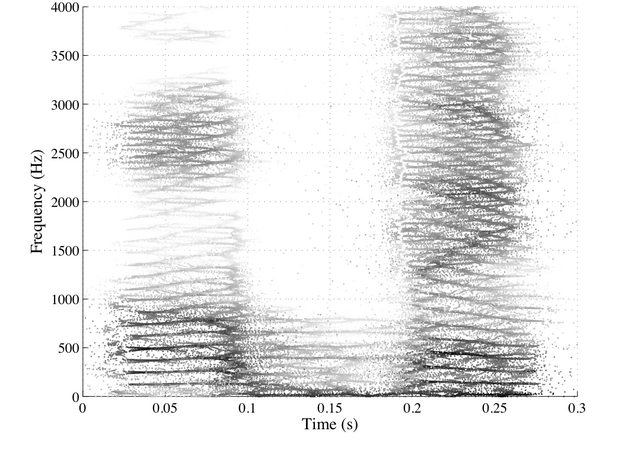
Спектрограмма слова «открытый» с переназначением длинного окна, рассчитанная с использованием окна Кайзера 54,4 мс с параметром формирования 9, подчеркивающим гармоники.
Спектрограмма слова «открытый» с переназначением короткого окна, рассчитанная с использованием окна Кайзера длительностью 13,6 мс с параметром формирования 9, подчеркивающим форманты и голосовые импульсы.

В общем, существует бесконечное количество одинаково допустимых разложений многокомпонентного сигнала. Свойство отделимости необходимо рассматривать в контексте желаемого разложения. Например, при анализе речевого сигнала окно анализа, длинное по отношению к времени между голосовыми импульсами, достаточно для разделения гармоник, но отдельные голосовые импульсы будут размыты, поскольку каждое окно охватывает множество импульсов (т. е. , отдельные импульсы не могут быть разделены во времени выбранным окном анализа). Окно анализа, которое намного короче, чем время между голосовыми импульсами, может разрешить голосовые импульсы, поскольку ни одно окно не охватывает более одного импульса, но частоты гармоник размазываются вместе, поскольку главный лепесток спектра окна анализа шире, чем интервал между гармониками (то есть гармоники не разделяются по частоте в выбранном окне анализа). ^[6]^: 2585

Расширения

Переназначение комплекса консенсуса

Гарднер и Магнаско (2006) утверждают, что слуховые нервы могут использовать разновидность метода переназначения для обработки звуков. Эти нервы известны тем, что сохраняют информацию о времени (фазе) лучше, чем о величинах. Авторы предлагают вариант переназначения со сложными значениями (т.е. как по фазе, так и по величине) и показывают, что он производит редкие выходные сигналы, как это делают слуховые нервы. Запуская это переназначение с окнами с разной полосой пропускания (см. обсуждение в разделе выше), обнаруживается «консенсус», который улавливает несколько типов сигналов, опять же, как и слуховая система. Они утверждают, что алгоритм достаточно прост для реализации нейронами. ^[8]

Синхронное преобразование

^[9]

Ссылки

^ Хейнсворт, Стивен (2003). «Глава 3: Методы переназначения». Методы автоматизированного анализа музыкального звука (доктор философии). Кембриджский университет. CiteSeerX 10.1.1.5.9579 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час Ф. Оже и П. Фландрин (май 1995 г.). «Улучшение читаемости частотно-временных и временных представлений методом переназначения». Транзакции IEEE по обработке сигналов . 43 (5): 1068–1089. Бибкод : 1995ITSP...43.1068A . CiteSeerX 10.1.1.646.794 . дои : 10.1109/78.382394 . S2CID 6336685 .
^ П. Фландрин, Ф. Оже и Э. Шассанд-Моттен, Переназначение частоты времени: От принципов к алгоритмам . в приложениях частотно-временной обработки сигналов (А. Папандреу-Суппаппола, ред.), гл. 5, стр. 179–203, CRC Press, 2003.
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час К. Кодера; Р. Гендрин и К. де Вильдари (февраль 1978 г.). «Анализ изменяющихся во времени сигналов с малыми значениями BT». Транзакции IEEE по акустике, речи и обработке сигналов . 26 (1): 64–76. дои : 10.1109/ТАССП.1978.1163047 .
^ Jump up to: ^а ^б Фитц, Келли Р.; Фулоп, Шон А. (2009). «Единая теория переназначения частоты времени». arXiv : 0903.3080 [ cs.SD ]. – эта рукопись препринта написана предыдущим автором этой статьи в Википедии; увидеть их вклад .
^ Jump up to: ^а ^б ^с DJ Нельсон (ноябрь 2001 г.). «Кроссспектральные методы обработки речи». Журнал Акустического общества Америки . 110 (5): 2575–2592. Бибкод : 2001ASAJ..110.2575N . дои : 10.1121/1.1402616 . ПМИД 11757947 .
^ К. Фитц, Л. Хакен, Об использовании частотно-временного переназначения в аддитивном моделировании звука, Журнал Общества аудиоинженеров 50 (11) (2002) 879–893.
^ Гарднер, Тимоти Дж.; Маньяско, Марсело О. (18 апреля 2006 г.). «Разреженные частотно-временные представления» . Труды Национальной академии наук . 103 (16): 6094–6099. Бибкод : 2006PNAS..103.6094G . дои : 10.1073/pnas.0601707103 . ПМЦ 1431718 . ПМИД 16601097 .
^ Мейнен, Сильвен; Оберлин, Томас; Фам, Дуонг-Хын (июль 2019 г.). «Синхросжатие преобразований: от низкочастотных к высокочастотным модуляциям и перспективам». Comptes Rendus Physique . 20 (5): 449–460. Бибкод : 2019CRPhy..20..449M . дои : 10.1016/j.crhy.2019.07.001 .

Дальнейшее чтение

С. А. Фулоп и К. Фитц, Спектрограмма для XXI века , Acoustics Today, vol. 2, нет. 3, стр. 26–33, 2006.
С. А. Фулоп и К. Фитц, Алгоритмы расчета спектрограммы мгновенной частоты (переназначенной) с поправкой по времени, с приложениями , Журнал Акустического общества Америки, том. 119, стр. 360–371, январь 2006 г.

Внешние ссылки

TFTB — Панель инструментов «Время-Частота»
SPEAR - Анализ и ресинтез синусоидального частичного редактирования
Loris — программное обеспечение с открытым исходным кодом для моделирования и морфинга звука.
SRA — веб-инструмент для исследования спектра и шероховатости звуковых сигналов. Архивировано 18 ноября 2019 г. в Wayback Machine (при поддержке гранта Северо-западного академического компьютерного консорциума Дж. Миддлтона, Университет Восточного Вашингтона).

[hainsworth-1] Хейнсворт, Стивен (2003). «Глава 3: Методы переназначения». Методы автоматизированного анализа музыкального звука (доктор философии). Кембриджский университет. CiteSeerX 10.1.1.5.9579 .

[improving-2] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час Ф. Оже и П. Фландрин (май 1995 г.). «Улучшение читаемости частотно-временных и временных представлений методом переназначения». Транзакции IEEE по обработке сигналов . 43 (5): 1068–1089. Бибкод : 1995ITSP...43.1068A . CiteSeerX 10.1.1.646.794 . дои : 10.1109/78.382394 . S2CID 6336685 .

[3] П. Фландрин, Ф. Оже и Э. Шассанд-Моттен, Переназначение частоты времени: От принципов к алгоритмам . в приложениях частотно-временной обработки сигналов (А. Папандреу-Суппаппола, ред.), гл. 5, стр. 179–203, CRC Press, 2003.

[Kodera-4] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час К. Кодера; Р. Гендрин и К. де Вильдари (февраль 1978 г.). «Анализ изменяющихся во времени сигналов с малыми значениями BT». Транзакции IEEE по акустике, речи и обработке сигналов . 26 (1): 64–76. дои : 10.1109/ТАССП.1978.1163047 .

[Fitz09-5] Jump up to: ^а ^б Фитц, Келли Р.; Фулоп, Шон А. (2009). «Единая теория переназначения частоты времени». arXiv : 0903.3080 [ cs.SD ]. – эта рукопись препринта написана предыдущим автором этой статьи в Википедии; увидеть их вклад .

[crossspectral-6] Jump up to: ^а ^б ^с DJ Нельсон (ноябрь 2001 г.). «Кроссспектральные методы обработки речи». Журнал Акустического общества Америки . 110 (5): 2575–2592. Бибкод : 2001ASAJ..110.2575N . дои : 10.1121/1.1402616 . ПМИД 11757947 .

[7] К. Фитц, Л. Хакен, Об использовании частотно-временного переназначения в аддитивном моделировании звука, Журнал Общества аудиоинженеров 50 (11) (2002) 879–893.

[Gar06-8] Гарднер, Тимоти Дж.; Маньяско, Марсело О. (18 апреля 2006 г.). «Разреженные частотно-временные представления» . Труды Национальной академии наук . 103 (16): 6094–6099. Бибкод : 2006PNAS..103.6094G . дои : 10.1073/pnas.0601707103 . ПМЦ 1431718 . ПМИД 16601097 .

[Meignen19-9] Мейнен, Сильвен; Оберлин, Томас; Фам, Дуонг-Хын (июль 2019 г.). «Синхросжатие преобразований: от низкочастотных к высокочастотным модуляциям и перспективам». Comptes Rendus Physique . 20 (5): 449–460. Бибкод : 2019CRPhy..20..449M . дои : 10.1016/j.crhy.2019.07.001 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]