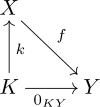Ядро (теория категорий)

В теории категорий и ее приложениях к другим разделам ядра математики являются обобщением ядер гомоморфизмов групп , ядер гомоморфизмов модулей и некоторых других ядер из алгебры . Интуитивно понятно, что ядро морфизма f : X → Y — это «наиболее общий» морфизм k : K → X , который дает ноль при составлении с (за которым следует) f .

Обратите внимание, что пары ядер и разностные ядра (также известные как двоичные эквалайзеры ) иногда называются «ядром»; хотя они и связаны, это не совсем одно и то же и не обсуждается в этой статье.

Определение [ править ]

Пусть C — категория .Чтобы определить ядро в общем теоретико-категорном смысле, C должен иметь нулевые морфизмы .В этом случае, если : X → Y — произвольный морфизм в C , то ядро f является эквалайзером f f и нулевого морфизма X в Y. из В символах:

кер( ж ) = eq( ж , 0 _XY )

следующее универсальное свойство Чтобы быть более явным, можно использовать . Ядро f — это объект K вместе с морфизмом k : K → X такой, что:

f ∘ k — нулевой морфизм из K в Y ;

Для любого морфизма k ′ : K ′ → X такого, что f ∘ k ′ является нулевым морфизмом, существует единственный морфизм u : K ′ → K такой, что k ∘ u = k ′ .

Что касается всякого универсального свойства, то существует единственный изоморфизм между двумя ядрами одного и того же морфизма, и морфизм k всегда является мономорфизмом (в категорическом смысле). Итак, принято говорить о ядре морфизма. Таким образом, в конкретных категориях можно взять подмножество K ′ , и вместо K в этом случае морфизм k является отображением включения . Это позволяет говорить о K как о ядре, поскольку f неявно определяется K . Существуют неконкретные категории, в которых аналогичным образом можно определить «естественное» ядро, такое, что K определяет k неявно.

Не каждый морфизм должен иметь ядро, но если оно есть, то все его ядра изоморфны в сильном смысле: если k : K → X и $ℓ : L \to X$ являются ядрами f : X → Y , то существует единственный изоморфизм φ: K → L такой, что $ℓ$ ∘φ = k .

Примеры [ править ]

Ядра известны во многих категориях абстрактной алгебры , таких как категория групп или категория (левых) модулей над фиксированным кольцом (включая векторные пространства над фиксированным полем ). Для ясности: если f : X → Y — гомоморфизм этих категорий, а K — ее ядро в обычном алгебраическом смысле , то K — подалгебра X в одной из , а гомоморфизм включения из K в X — ядро в категорический смысл.

Обратите внимание, что в категории моноидов теоретико-категорные ядра существуют так же, как и для групп, но эти ядра не несут достаточной информации для алгебраических целей. Следовательно, понятие ядра, изучаемое в теории моноида, немного отличается (см. #Отношение к алгебраическим ядрам ниже).

В категории колец с единицей нет ядер в теоретико-категорном смысле; более того, эта категория даже не имеет нулевых морфизмов. Тем не менее, в теории колец до сих пор изучается понятие ядра, соответствующее ядрам в категории неединичных колец .

В категории точечных топологических пространств , если f : X → Y — непрерывное точечное отображение, то прообраз отмеченной точки K является подпространством X . Отображение включения K в X является категориальным ядром f .

с другими категориальными Связь понятиями

Двойственной концепции ядра является концепция cokernel .То есть ядром морфизма является его коядро в противоположной категории , и наоборот.

Как упоминалось выше, ядро — это разновидность двоичного эквалайзера или разностного ядра .И наоборот, в преаддитивной категории каждый двоичный эквалайзер может быть построен как ядро.Точнее, эквалайзер морфизмов f и g является ядром разности g − f .В символах:

eq ( ж , г ) знак равно ker ( г - ж ).

Именно из-за этого бинарные эквалайзеры называются «разностными ядрами» даже в непредаддитивных категориях, где морфизмы не могут быть вычтены.

Каждое ядро, как и любой другой эквалайзер, является мономорфизмом .И наоборот, мономорфизм называется нормальным, если он является ядром некоторого морфизма.Категория называется нормальной , если любой мономорфизм нормален.

В частности, абелевы категории всегда нормальны.В этой ситуации ядро коядра любого морфизма (который всегда существует в абелевой категории) оказывается образом этого морфизма; в символах:

im f = ker coker f (в абелевой категории)

Когда m — мономорфизм, он должен быть собственным образом; таким образом, абелевы категории не только нормальны, так что каждый мономорфизм является ядром, но мы также знаем, какой морфизм является ядром мономорфизма, а именно его коядра.В символах:

m = ker (coker m ) (для мономорфизмов в абелевой категории)

с алгебраическими Связь ядрами

Универсальная алгебра определяет понятие ядра для гомоморфизмов между двумя алгебраическими структурами одного и того же типа.Это понятие ядра измеряет, насколько данный гомоморфизм далек от инъективности .Между этим алгебраическим понятием и категориальным понятием ядра есть некоторое совпадение, поскольку оба они обобщают ситуацию групп и модулей, упомянутых выше.Однако в целом универсально-алгебраическое понятие ядра больше похоже на теоретико-категорное понятие пары ядер .В частности, пары ядер можно использовать для интерпретации ядер в теории моноидов или теории колец в терминах теории категорий.

Источники [ править ]

Аводи, Стив (2010) [2006]. Теория категорий (PDF) . Оксфордские руководства по логике. Том. 49 (2-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-923718-0 . Архивировано из оригинала (PDF) 21 мая 2018 г. Проверено 29 июня 2018 г.
Ядро в n Lab