Баллистическая проводимость

В мезоскопической физике баллистическая проводимость ( баллистический транспорт ) — это беспрепятственный поток (или транспорт ) носителей заряда (обычно электронов ) или частиц, несущих энергию, на относительно большие расстояния в материале. В общем, удельное сопротивление материала существует потому, что электрон, двигаясь внутри среды, рассеивается примесями, дефектами , тепловыми колебаниями ионов в кристаллическом твердом теле или, вообще, любым свободно движущимся атомом/молекулой, составляющим газ. или жидкость. Без рассеяния электроны просто подчиняются второму закону движения Ньютона на нерелятивистских скоростях .

Среднюю длину свободного пробега частицы можно описать как среднюю длину, которую частица может свободно перемещать, т. е. до столкновения, которое могло бы изменить ее импульс. Длину свободного пробега можно увеличить, уменьшив количество примесей в кристалле или понизив его температуру. Баллистический транспорт наблюдается, когда средняя длина свободного пробега частицы (намного) длиннее, чем размер среды, через которую движется частица. Частица меняет свое движение только при столкновении со стенками . В случае провода, подвешенного в воздухе/вакууме, поверхность провода играет роль ящика, отражающего электроны и препятствующего их выходу в пустое пространство/открытый воздух. Это связано с тем, что для извлечения электрона из среды необходимо заплатить энергию ( работа выхода ).

Баллистическая проводимость обычно наблюдается в квазиодномерных структурах, таких как углеродные нанотрубки или кремниевые нанопроволоки , из-за экстремальных эффектов размерного квантования в этих материалах. Баллистическая проводимость не ограничивается электронами (или дырками), но также может применяться и к фононам . Теоретически возможно распространение баллистической проводимости на другие квазичастицы, но это не подтверждено экспериментально. В качестве конкретного примера баллистический транспорт можно наблюдать в металлической нанопроволоке : из-за небольшого размера проволоки ( нанометровый масштаб или 10 ⁻⁹ метров) и средняя длина свободного пробега, которая может быть больше, чем в металле. ^[1]

Баллистическая проводимость отличается от сверхпроводимости 1) конечным ненулевым сопротивлением и 2) отсутствием эффекта Мейснера в материале. Наличие сопротивления подразумевает, что тепло рассеивается в выводах за пределами «баллистического» проводника, где могут иметь место эффекты неупругого рассеяния.

Теория

Механизмы рассеяния

В общем, авианосцы демонстрируют баллистическую проводимость, когда $L\leq \lambda _{\rm {MFP}}$ где $L$ — длина активной части устройства (например, канала в MOSFET ). $\lambda _{\rm {MFP}}$ — это средняя длина свободного пробега носителя, которую можно определить по правилу Маттиссена , записанному здесь для электронов:

{\frac {1}{\lambda _{\mathrm {MFP} }}}={\frac {1}{\lambda _{\mathrm {el-el} }}}+{\frac {1}{\lambda _{\mathrm {ap} }}}+{\frac {1}{\lambda _{\mathrm {op,ems} }}}+{\frac {1}{\lambda _{\mathrm {op,abs} }}}+{\frac {1}{\lambda _{\mathrm {impurity} }}}+{\frac {1}{\lambda _{\mathrm {defect} }}}+{\frac {1}{\lambda _{\mathrm {boundary} }}}

где

$\lambda _{\mathrm {el-el} }$ - длина электрон-электронного рассеяния,
$\lambda _{\mathrm {ap} }$ – длина рассеяния акустических фононов (испускания и поглощения),
$\lambda _{\mathrm {op,ems} }$ – длина рассеяния излучения оптических фононов,
$\lambda _{\mathrm {op,abs} }$ – длина рассеяния оптического фонона при поглощении,
$\lambda _{\mathrm {impurity} }$ – длина рассеяния электронов на примеси,
$\lambda _{\mathrm {defect} }$ – длина рассеяния электронов на дефектах,
и $\lambda _{\mathrm {boundary} }$ – длина рассеяния электрона на границе.

В механизмах рассеяния обычно доминирует излучение оптических фононов , что зависит от материала и условий транспортировки. Существуют также другие механизмы рассеяния, применимые к различным носителям, которые здесь не рассматриваются (например, рассеяние фононов на удаленной границе раздела, рассеяние переброса ). Чтобы получить эти характерные скорости рассеяния, нужно было бы вывести гамильтониан и решить золотое правило Ферми для рассматриваемой системы.

Формализм Ландауэра – Бюттикера

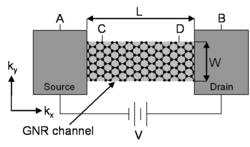
В 1957 году Рольф Ландауэр предположил, что проводимость в одномерной системе можно рассматривать как проблему передачи. Для одномерного с нанолентой графена полевого транзистора (GNR-FET) справа (где канал предполагается баллистическим) ток от A до B, определяемый уравнением переноса Больцмана , равен

I_{\rm {AB}}={\frac {g_{\text{s}}e}{h}}\int _{E_{\rm {F_{B}}}}^{E_{\rm {F_{A}}}}M(E)f^{\prime }(E)T(E)dE

,

где g _s = 2, из-за спинового вырождения , e — заряд электрона, h — постоянная Планка , $E_{\rm {F_{A}}}$ и $E_{\rm {F_{B}}}$ — уровни Ферми A и B , M ( E ) — число распространяющихся мод в канале, f ’( E ) — отклонение от равновесного распределения электронов (возмущение), а T(E) — вероятность передачи ( Т = 1 для баллистики). ^{[ нужна ссылка ]} На основе определения проводимости

G={\frac {I}{V}}

,

а расстояние по напряжению между уровнями Ферми составляет примерно $eV=E_{\rm {F_{A}}}-E_{\rm {F_{B}}}$ , отсюда следует, что

G=G_{0}MT

, с

G_{0}={\frac {2e^{2}}{h}}

где M — количество мод в канале передачи, включая спин. $G_{0}$ известен как квант проводимости . Контакты имеют множество режимов за счет большего размера по сравнению с каналом. И наоборот, квантовое ограничение в канале 1D GNR ограничивает количество мод вырождением носителей и ограничениями, налагаемыми соотношением дисперсии энергии и зоной Бриллюэна . Например, электроны в углеродных нанотрубках имеют две междолинные моды и две спиновые моды. Так как контакты и канал ГНР соединены выводами, то вероятность передачи меньше на контактах А и Б ,

T\approx {\frac {M}{M_{\rm {contact}}}}

.

Таким образом, квантовая проводимость примерно одинакова, если ее измерить в точках A и B или C и D.

Формализм Ландауэра-Бюттикера справедлив до тех пор, пока несущие когерентны (что означает, что длина активного канала меньше средней длины свободного пробега при нарушении фазы), а функции передачи можно рассчитать по уравнению Шредингера или аппроксимировать с помощью квазиклассических приближений , например ВКБ приближение . Следовательно, даже в случае идеального баллистического транспорта существует фундаментальная баллистическая проводимость, которая насыщает ток устройства с сопротивлением примерно 12,9 кОм на моду (включая спиновое вырождение). ^[2] Однако существует обобщение формализма переноса Ландауэра-Бюттикера, применимое к нестационарным задачам при наличии диссипации . ^[3]^[4]

Важность

Баллистическая проводимость позволяет использовать квантово-механические электронов свойства волновых функций . Баллистический перенос является когерентным с точки зрения волновой механики . Такие явления, как двухщелевая интерференция , пространственный резонанс (и другие оптические или микроволновые эффекты) могут быть использованы в электронных системах на наномасштабе, в системах, включающих нанопроволоки и нанотрубки .

Широко распространенное явление электрического контактного сопротивления или ECR возникает, когда электрический ток, протекающий через шероховатую поверхность раздела, ограничивается ограниченным количеством пятен контакта. Размер и распределение этих пятен контакта определяются топологической структурой контактирующих поверхностей, образующих электрический контакт. В частности, для поверхностей с высокой фрактальной размерностью пятна контакта могут быть очень маленькими. В таких случаях, когда радиус пятна контакта меньше длины свободного пробега электронов $\lambda$ В сопротивлении преобладает механизм Шарвина, при котором электроны баллистически проходят через эти микроконтакты с сопротивлением, которое можно описать следующим образом: ^[5]

R_{\rm {S}}={\frac {\lambda (\rho _{1}+\rho _{2})}{2a}}.

Этот термин, где $\rho _{1}$ и $\rho _{2}$ соответствуют удельному сопротивлению двух контактирующих поверхностей, известному как сопротивление Шарвина. Электрические контакты, приводящие к баллистической электронной проводимости, известны как контакты Шарвина . Когда радиус пятна контакта больше длины свободного пробега электронов, контактное сопротивление можно рассматривать классически.

Оптические аналогии

Сравнение со светом дает аналогию между баллистической и небаллистической проводимостью. Баллистические электроны ведут себя как свет в волноводе или высококачественной оптической сборке. Небаллистические электроны ведут себя как свет, рассеянный в молоке или отраженный от белой стены или листа бумаги.

Электроны могут рассеиваться в проводнике несколькими способами. Электроны обладают несколькими свойствами: длиной волны (энергией), направлением, фазой и ориентацией спина. Разные материалы имеют разную вероятность рассеяния, что приводит к разной степени некогерентности (стохастичности). Некоторые виды рассеяния могут вызвать только изменение направления электронов, другие могут вызвать потерю энергии.

Рассмотрим когерентный источник электронов, подключенный к проводнику. На ограниченном расстоянии волновая функция электрона останется когерентной. Вы по-прежнему можете детерминированно предсказать его поведение (и теоретически использовать его для вычислений). После некоторого большего расстояния рассеяние приводит к тому, что каждый электрон имеет немного другую фазу и/или направление. Но потерь энергии по-прежнему почти нет. Подобно монохроматическому свету, проходящему через молоко, электроны подвергаются упругим взаимодействиям. Информация о состоянии электронов на входе при этом теряется. Транспорт становится статистическим и стохастическим . С точки зрения сопротивления стохастическое (неориентированное) движение электронов бесполезно, даже если они несут одинаковую энергию – они движутся термически. Если электроны тоже подвергаются неупругим взаимодействиям, они теряют энергию, и в результате возникает второй механизм сопротивления. Электроны, которые подвергаются неупругому взаимодействию, подобны немонохроматическому свету.

Для корректного использования этой аналогии необходимо учитывать несколько фактов:

фотоны — бозоны , а электроны — фермионы ;
между электронами существует кулоновское отталкивание , поэтому эта аналогия хороша только для одноэлектронной проводимости, поскольку электронные процессы сильно нелинейны и зависят от других электронов;
более вероятно, что электрон потеряет больше энергии, чем фотон, из-за ненулевой массы покоя электрона ;
Взаимодействия электронов с окружающей средой, друг другом и другими частицами обычно сильнее, чем взаимодействия с фотонами и между ними.

Примеры

Как уже упоминалось, наноструктуры, такие как углеродные нанотрубки или графеновые наноленты, часто считаются баллистическими, но эти устройства лишь очень близко напоминают баллистическую проводимость. Их баллистичность составляет около 0,9 при комнатной температуре. ^[6]

Углеродные нанотрубки и графеновая нанолента

Доминирующим механизмом рассеяния при комнатной температуре является механизм испускания электронов оптических фононов. Если электроны не рассеиваются с достаточным количеством фононов (например, если скорость рассеяния низкая), средняя длина свободного пробега имеет тенденцию быть очень длинной ( $\lambda _{MFP}\approx 1{\mu }$ м). Таким образом, нанотрубка или графеновая нанолента могут быть хорошим баллистическим проводником, если транспортные электроны не рассеиваются на слишком много фононов и если длина устройства составляет около 100 нм. Обнаружено, что такой режим транспорта зависит от структуры края наноленты и энергии электронов. ^[7]

Изотопно-обогащенный алмаз

Изотопически чистый алмаз может иметь значительно более высокую теплопроводность. См. Список теплопроводностей . ^{[ нужна ссылка ]}

См. также

Адиабатическая схема - электронные схемы малой мощности, использующие обратимую логику для экономии энергии.
Баллистический коллекторный транзистор
Транзистор баллистического отклонения - транзистор, в котором вместо логического элемента используются электромагнитные силы.
Превышение скорости

Ссылки

^ Такаянаги, Кунио; Кондо, Юкихито; Ониси, Хидеаки (2001). «Подвесные золотые нанопроволоки: баллистический транспорт электронов». JSAP International . 3 (9). S2CID 28636503 .
^ Суприё Датта (1997). Электронный транспорт в мезоскопических системах . Харун Ахмад, Алек Броерс, Майкл Пеппер. Нью-Йорк: Издательство Кембриджского университета. стр. 57–111. ISBN 978-0-521-59943-6 .
^ Паставски, Орасио М. (15 сентября 1991 г.). «Классический и квантовый перенос из обобщенных уравнений Ландауэра-Бюттикера». Физический обзор B . 44 (12): 6329–6339. Бибкод : 1991PhRvB..44.6329P . дои : 10.1103/PhysRevB.44.6329 . ПМИД 9998497 .
^ Паставски, Орасио М. (15 августа 1992 г.). «Классический и квантовый перенос из обобщенных уравнений Ландауэра-Буттикера. II. Резонансное туннелирование, зависящее от времени». Physical Review B. 46 ( 7): 4053–4070. Bibcode : 1992PhRvB..46.4053P . doi : 10.1103/PhysRevB.46.4053 . PMID 10004135 .
^ Чжай, К; и др. (2016). «Межфазное электромеханическое поведение на шероховатых поверхностях» (PDF) . Письма по экстремальной механике . 9 : 422–429. Бибкод : 2016ExML....9..422Z . дои : 10.1016/j.eml.2016.03.021 . hdl : 1959.4/unsworks_60452 .
^ Косватта, Сиюранга О.; Хасан, Сайед; Лундстрем, Марк С.; Анантрам, член парламента; Никонов, Дмитрий Евгеньевич (10 июля 2006 г.). «Баллистичность полевых транзисторов на нанотрубках: роль энергии фононов и смещения затвора». Письма по прикладной физике . 89 (2): 023125. arXiv : cond-mat/0511723 . Бибкод : 2006ApPhL..89b3125K . дои : 10.1063/1.2218322 . ISSN 0003-6951 . S2CID 44232115 .
^ Кох, Матиас; Эмпл, Франциско; Иоахим, Кристиан; Гриль, Леонард (14 октября 2012 г.). «Зависимая от напряжения проводимость одиночной графеновой наноленты» . Природные нанотехнологии . 7 (11): 713–717. Бибкод : 2012НатНа...7..713К . дои : 10.1038/nnano.2012.169 . ISSN 1748-3387 . ПМИД 23064554 . ^{[ постоянная мертвая ссылка ]}

Дальнейшее чтение

Ду, Сюй; Скачко Иван; Баркер, Энтони; Андрей, Ева Ю. (20 июля 2008 г.). «Приближение к баллистическому транспорту во взвешенном графене». Природные нанотехнологии . 3 (8): 491–495. arXiv : 0802.2933 . Бибкод : 2008NatNa...3..491D . дои : 10.1038/nnano.2008.199 . ISSN 1748-3387 . ПМИД 18685637 . S2CID 118441080 .
Жалаберт, РА; Пишар, Ж.-Л.; Бинаккер, CWJ (1994). «Универсальные квантовые признаки хаоса в баллистическом транспорте». EPL (Письма по еврофизике) . 27 (4): 255. arXiv : cond-mat/9403073 . Бибкод : 1994EL.....27..255J . дои : 10.1209/0295-5075/27/4/001 . ISSN 0295-5075 . S2CID 55864480 .

[1] Такаянаги, Кунио; Кондо, Юкихито; Ониси, Хидеаки (2001). «Подвесные золотые нанопроволоки: баллистический транспорт электронов». JSAP International . 3 (9). S2CID 28636503 .

[Datta-2] Суприё Датта (1997). Электронный транспорт в мезоскопических системах . Харун Ахмад, Алек Броерс, Майкл Пеппер. Нью-Йорк: Издательство Кембриджского университета. стр. 57–111. ISBN 978-0-521-59943-6 .

[3] Паставски, Орасио М. (15 сентября 1991 г.). «Классический и квантовый перенос из обобщенных уравнений Ландауэра-Бюттикера». Физический обзор B . 44 (12): 6329–6339. Бибкод : 1991PhRvB..44.6329P . дои : 10.1103/PhysRevB.44.6329 . ПМИД 9998497 .

[4] Паставски, Орасио М. (15 августа 1992 г.). «Классический и квантовый перенос из обобщенных уравнений Ландауэра-Буттикера. II. Резонансное туннелирование, зависящее от времени». Physical Review B. 46 ( 7): 4053–4070. Bibcode : 1992PhRvB..46.4053P . doi : 10.1103/PhysRevB.46.4053 . PMID 10004135 .

[5] Чжай, К; и др. (2016). «Межфазное электромеханическое поведение на шероховатых поверхностях» (PDF) . Письма по экстремальной механике . 9 : 422–429. Бибкод : 2016ExML....9..422Z . дои : 10.1016/j.eml.2016.03.021 . hdl : 1959.4/unsworks_60452 .

[6] Косватта, Сиюранга О.; Хасан, Сайед; Лундстрем, Марк С.; Анантрам, член парламента; Никонов, Дмитрий Евгеньевич (10 июля 2006 г.). «Баллистичность полевых транзисторов на нанотрубках: роль энергии фононов и смещения затвора». Письма по прикладной физике . 89 (2): 023125. arXiv : cond-mat/0511723 . Бибкод : 2006ApPhL..89b3125K . дои : 10.1063/1.2218322 . ISSN 0003-6951 . S2CID 44232115 .

[7] Кох, Матиас; Эмпл, Франциско; Иоахим, Кристиан; Гриль, Леонард (14 октября 2012 г.). «Зависимая от напряжения проводимость одиночной графеновой наноленты» . Природные нанотехнологии . 7 (11): 713–717. Бибкод : 2012НатНа...7..713К . дои : 10.1038/nnano.2012.169 . ISSN 1748-3387 . ПМИД 23064554 . ^{[ постоянная мертвая ссылка ]}

[1]

[2]

[3]

[4]

[5]

[6]

[7]