Модель Кирала Поттса

Киральная модель Поттса — это модель спина на плоской решетке в статистической механике, которую изучали, среди прочего, Хелен Ау-Янг Перк и Жак Перк. Ее можно рассматривать как обобщение модели Поттса , и, как и модель Поттса , модель определяется конфигурациями, которые представляют собой назначения спинов каждой вершине графа , где каждый спин может принимать одно из значений. $N$ ценности. К каждому ребру, соединяющему вершины с назначенными спинами $n$ и $n'$, вес Больцмана $W(n,n')$ назначено. Для этой модели хиральность означает, что $W(n,n')\neq W(n',n)$. Когда веса удовлетворяют уравнению Янга-Бакстера , оно интегрируемо в том смысле, что определенные величины могут быть точно оценены.

Для интегрируемой киральной модели Поттса веса определяются кривой высокого , рода киральной кривой Поттса . В отличие от других решаемых моделей, чьи веса параметризованы кривыми рода меньше или равными единице, так что их можно выразить через тригонометрические функции, рациональные функции для случая нулевого рода или тэта-функции для случая рода 1, эта модель включает в себя тэта высокого рода функции, для которых теория менее разработана.

Соответствующая модель киральных часов , которая была независимо представлена ​​в 1980-х годах Дэвидом Хьюзом и Стелланом Остлундом, не совсем разрешима, в отличие от киральной модели Поттса.

Модель

Эта модель выходит за рамки всех ранее известных моделей и поднимает массу нерешенных вопросов, связанных с некоторыми из наиболее трудноразрешимых проблем алгебраической геометрии , которые существуют с нами уже 150 лет. Киральные модели Поттса используются для понимания фазовых переходов соизмеримо-несоизмеримо. Для N = 3 и 4 интегрируемый случай был обнаружен в 1986 году в Стоуни-Брук и опубликован в следующем году.

Самодвойственный случай

Модель называется самодвойственной, если преобразование Фурье весовой функции возвращает ту же функцию. Особый (род 1) случай был раскрыт в 1982 году Фатеевым и Замолодчиковым . Сняв некоторые ограничения работы Алькараса и Сантоса, был открыт более общий самодвойственный случай интегрируемой киральной модели Поттса. Вес указан в виде продукта. и показано, что параметры веса находятся на кривой Ферма с родом больше 1.

Общий случай

Было найдено общее решение для всех k (температурной переменной). Веса также были заданы в форме произведения, и было проверено вычислительно (на Фортране ), что они удовлетворяют соотношению звезда-треугольник. Доказательство было опубликовано позже.

Результаты

Параметр заказа

Из серии был параметр порядка предположен иметь простую форму $$\langle \sigma ^{n}\rangle =(1-k'^{2})^{\beta },\quad \beta =n(N-n)/2N^{2}.$$Чтобы доказать эту гипотезу, потребовалось много лет, поскольку обычный метод угловой матрицы переноса нельзя было использовать из-за более высокой кривой рода. Эту гипотезу доказал Бакстер в 2005 году. используя функциональные уравнения и метод «ломаной линии быстроты» Джимбо и др. предполагая две умеренные аналитичности условия типа, обычно используемого в области интегрируемых моделей Янга–Бакстера. Совсем недавно в серии статей был дан алгебраический ( подобный Изингу ) способ получения параметра порядка, дающий больше понимания алгебраической структуры.

Подключение к шестивершинной модели

В 1990 году Бажанов и Строганов показал, что существуют L -операторы ( оператор Лакса ), удовлетворяющие уравнению Янга–Бакстера

$L_{i_{1}\alpha }^{j_{1}\beta }(x)L_{i_{2}\beta }^{j_{2}\gamma }(y)R_{j_{1}j_{2}}^{k_{1}k_{2}}(y/x)=R_{i_{1}i_{2}}^{j_{1}j_{2}}(y/x)L_{j_{2}\alpha }^{k_{2}\beta }(y)L_{j_{1}\beta }^{k_{1}\gamma }(x),\quad 0<i,j,k\leq 1,\quad 0\leq \alpha ,\beta ,\gamma \leq N-1.$

где 2 × 2 R -оператор ( R-матрица ) — это шестивершинная R -матрица модели (см. Вершинная модель ). Было показано, что произведение четырех киральных весов Поттса S переплетает два L -оператора как

$L_{i_{1}\alpha _{1}}^{i_{2}\alpha _{2}}{\hat {L}}_{i_{2}\beta _{1}}^{i_{3}\beta _{2}}S_{\alpha _{2}\beta _{2}}^{\alpha _{3}\beta _{3}}=S_{\alpha _{1}\beta _{1}}^{\alpha _{2}\beta _{2}}{\hat {L}}_{i_{1}\beta _{2}}^{i_{2}\beta _{3}}L_{i_{2}\alpha _{2}}^{i_{3}\alpha _{3}},\quad 0<i_{i}\leq 1,\quad 0\leq \alpha _{i},\beta _{i}\leq N-1.$

Это вдохновило на прорыв: были открыты функциональные соотношения для трансфер-матриц киральных моделей Поттса.

Свободная энергия и межфазное натяжение

Используя эти функциональные соотношения, Бакстер смог вычислить собственные значения матрицы переноса киральной модели Поттса: и получил критический показатель для удельной теплоемкости α=1-2/N, о котором также предполагалось в ссылке 12. Межфазное натяжение было также рассчитано им с показателем степени µ=1/2+1/N.

Связь с теорией узлов

Интегрируемые киральные веса Поттса заданы в виде произведения как

$W_{pq}(n)\!=\!{\Big (}{\mu _{p} \over \mu _{q}}{\Big )}^{\!\!n}\prod _{j=1}^{n}{y_{q}-x_{p}\omega ^{j} \over y_{p}-x_{q}\omega ^{j}},\quad {\overline {W}}_{pq}(n)\!=\!{\big (}{\mu _{p}\mu _{q}}{\big )}^{\!n}\!\prod _{j=1}^{n}{\omega x_{p}\!-\!x_{q}\omega ^{j} \over y_{q}\!-\!y_{p}\omega ^{j}},$

где $\omega ^{N}=1$ является примитивным корнем из единицы , и мы связываем с каждой переменной быстроты p три переменные $(x_{p},y_{p},\mu _{p})$ удовлетворяющий

$x_{p}^{N}+y_{p}^{N}=k(1+x_{p}^{N}y_{p}^{N}),\quad k'^{2}+k^{2}=1,\quad k'\mu _{p}^{N}=1-ky_{p}^{N},\quad k'\mu _{p}^{-N}=1-kx_{p}^{N}.$

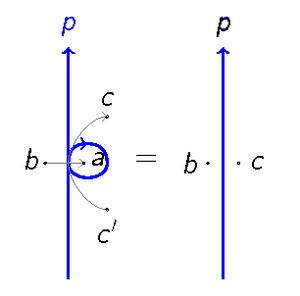
Это легко увидеть

$W_{pp}(a-b)=1,\quad {\overline {W}}_{pp}(a-b)=\delta _{a,b}$

что аналогично ходу I Райдемейстера . Также было известно, что веса удовлетворяют соотношению инверсии:

$W_{pq}(a-b)W_{qp}(a-b)=1,\quad \sum _{d=0}^{N-1}{\overline {W}}_{pq}(a-d){\overline {W}}_{qp}(d-a')=r_{pq}\delta _{a,a'}.$

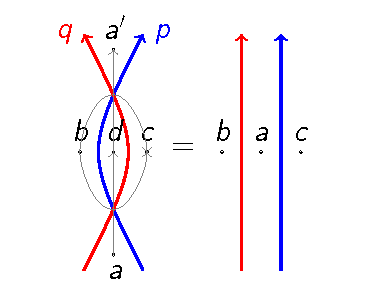
Это эквивалентно второму ходу Рейдемейстера. Отношение звезда-треугольник

$\sum _{d=1}^{N}\,{\overline {W}}_{pr}(a-d)\,W_{pq}(d-c)\,{\overline {W}}_{rq}(d-b)=R_{pqr}\,{\overline {W}}_{pq}(a-b)\,{W}_{pr}(b-c)\,W_{rq}(a-c)$

эквивалентен третьему ходу Рейдемейстера. Они показаны на рисунках ниже.

Свойство гирь: ход Рейдемейстера I

Инверсионное соотношение весов: ход Райдемейстера II

Отношение звезда-треугольник: ход Рейдемейстера III

Веса интегрируемых киральных моделей Поттса

См. также

• Модель ZN