Воздушная масса (астрономия)

«Авиамасса» перенаправляется сюда. Чтобы узнать о других значениях, см. Воздушная масса (значения) .

В астрономии земной воздушная масса или воздушная масса — это мера количества воздуха вдоль луча зрения при наблюдении звезды или другого небесного источника из-под атмосферы ( Green 1992 ). Он формулируется как интеграл плотности воздуха вдоль светового луча .

Проникая в атмосферу , свет ослабляется за счет рассеяния и поглощения ; чем толще атмосфера, через которую он проходит, тем больше затухание . Следовательно, небесные тела ближе к горизонту кажутся менее яркими, чем ближе к зениту . Это затухание, известное как атмосферное поглощение , количественно описывается законом Бера-Ламберта .

«Воздушная масса» обычно указывает на относительную воздушную массу , соотношение абсолютных воздушных масс (как определено выше) при наклонном падении относительно массы воздуха в зените . Итак, по определению относительная воздушная масса в зените равна 1. Воздушная масса увеличивается по мере увеличения угла между источником и зенитом, достигая значения примерно 38 на горизонте. Воздушная масса может быть меньше единицы на высоте выше уровня моря ; однако большинство выражений для воздушной массы в закрытой форме не учитывают влияние высоты наблюдателя, поэтому корректировку обычно необходимо выполнять другими способами.

Таблицы воздушных масс были опубликованы многочисленными авторами, в том числе Бемпорадом (1904) , Алленом (1973) , и Кастен и Янг (1989) .

Определение

Абсолютная воздушная масса определяется как: $$\sigma =\int \rho \,\mathrm {d} s\,.$$где $\rho$ - плотность воздуха . объемная Таким образом $\sigma$ — это тип плотности наклонных столбцов .

В вертикальном направлении абсолютная масса воздуха в зените равна: $$\sigma _{\mathrm {zen} }=\int \rho \,\mathrm {d} z$$

Так $\sigma _{\mathrm {zen} }$ это тип плотности вертикального столбца .

Наконец, относительная воздушная масса равна: $$X={\frac {\sigma }{\sigma _{\mathrm {zen} }}}$$

Считая плотность воздуха однородной, можно исключить ее из интегралов. Абсолютная воздушная масса затем упрощается до продукта: $$\sigma ={\bar {\rho }}s$$где ${\bar {\rho }}=\mathrm {const.}$ - средняя плотность и длина дуги $s$ косых и зенитных световых путей: $${\begin{aligned}s&=\int \,\mathrm {d} s\\s_{\mathrm {zen} }&=\int \,\mathrm {d} z\end{aligned}}$$

В соответствующей упрощенной относительной воздушной массе средняя плотность сокращается в дроби, что приводит к отношению длин путей: $$X={\frac {s}{s_{\mathrm {zen} }}}\,.$$

Часто делаются дальнейшие упрощения, предполагающие прямолинейное распространение (пренебрегая изгибом луча), как обсуждается ниже.

Расчет

Графики воздушной массы по различным формулам

Фон

Угол небесного тела с зенитом — это зенитный угол (в астрономии обычно называемый зенитным расстоянием ). Угловое положение тела также может быть задано через высоту , угол над геометрическим горизонтом; высота $h$ и зенитный угол $z$ связаны, таким образом, $$h=90^{\circ }-z\,.$$

Атмосферная рефракция заставляет свет, попадающий в атмосферу, следовать примерно по круговой траектории, которая немного длиннее геометрической траектории. Воздушные массы должны учитывать более длинный путь ( Young 1994 ). Кроме того, из-за рефракции небесное тело кажется выше над горизонтом, чем оно есть на самом деле; на горизонте разница между истинным зенитным углом и видимым зенитным углом составляет примерно 34 угловых минуты. Большинство формул воздушной массы основаны на видимом зенитном угле, но некоторые основаны на истинном зенитном угле, поэтому важно убедиться, что используется правильное значение, особенно вблизи горизонта.

Плоскопараллельная атмосфера

Когда зенитный угол мал или умерен, хорошим приближением является предположение об однородной плоскопараллельной атмосфере (т. е. атмосфере, в которой плотность постоянна и кривизна Земли игнорируется). Воздушная масса $X$ тогда это просто секанс зенитного угла $z$: $$X=\sec \,z\,.$$

При зенитном угле 60° воздушная масса равна примерно 2. Однако, поскольку Земля не плоская , эту формулу можно использовать только для зенитных углов примерно до 60–75°, в зависимости от требований к точности. При больших зенитных углах точность быстро падает. $X=\sec \,z$ становясь бесконечным на горизонте; воздушная масса горизонта в более реалистичной сферической атмосфере обычно меньше 40.

Интерполяционные формулы

Многие формулы были разработаны для соответствия табличным значениям воздушной массы; один из них, написанный Янгом и Ирвином (1967), включал простой корректирующий термин: $$X=\sec \,z_{\mathrm {t} }\,\left[1-0.0012\,(\sec ^{2}z_{\mathrm {t} }-1)\right]\,,$$где $z_{\mathrm {t} }$ это истинный зенитный угол. Это дает полезные результаты примерно до 80 °, но точность быстро ухудшается при больших зенитных углах. Рассчитанная воздушная масса достигает максимума 11,13 при 86,6°, становится нулевой при 88° и приближается к отрицательной бесконечности у горизонта. График этой формулы на прилагаемом графике включает поправку на атмосферную рефракцию, так что рассчитанная воздушная масса рассчитана для видимого, а не истинного зенитного угла.

Харди (1962) ввел полином в $\sec \,z-1$: $$X=\sec \,z\,-\,0.0018167\,(\sec \,z\,-\,1)\,-\,0.002875\,(\sec \,z\,-\,1)^{2}\,-\,0.0008083\,(\sec \,z\,-\,1)^{3}$$что дает полезные результаты для зенитных углов, возможно, до 85 °. Как и в предыдущей формуле, рассчитанная воздушная масса достигает максимума, а затем приближается к отрицательной бесконечности у горизонта.

Розенберг (1966) предложил $$X=\left(\cos \,z+0.025e^{-11\cos \,z}\right)^{-1}\,,$$что дает разумные результаты для больших зенитных углов с воздушной массой на горизонте 40.

Кастен и Янг (1989) разработали

$$X={\frac {1}{\cos \,z+0.50572\,(6.07995^{\circ }+90^{\circ }-z)^{-1.6364}}}\,,$$что дает приемлемые результаты для зенитных углов до 90° и воздушной массы около 38° на горизонте. Здесь второй $z$ срок в градусах .

Янг (1994) разработал $$X={\frac {1.002432\,\cos ^{2}z_{\mathrm {t} }+0.148386\,\cos \,z_{\mathrm {t} }+0.0096467}{\cos ^{3}z_{\mathrm {t} }+0.149864\,\cos ^{2}z_{\mathrm {t} }+0.0102963\,\cos \,z_{\mathrm {t} }+0.000303978}}\,$$по истинному зенитному углу $z_{\mathrm {t} }$, для которого он заявил, что максимальная ошибка (на горизонте) составляет 0,0037 воздушной массы.

Пикеринг (2002) разработал $$X={\frac {1}{\sin(h+{244}/(165+47h^{1.1}))}}\,,$$где $h$ видимая высота $(90^{\circ }-z)$ в градусах. имеет десятую ошибку Шефера (1998) . Пикеринг утверждал, что его уравнение вблизи горизонта

Атмосферные модели

Интерполяционные формулы пытаются обеспечить хорошее соответствие табличным значениям воздушной массы с минимальными вычислительными затратами. Однако табличные значения должны определяться на основе измерений или атмосферных моделей, основанных на геометрических и физических соображениях Земли и ее атмосферы.

Непреломляющая сферическая атмосфера

Влияние атмосферы на оптическую передачу можно смоделировать так, как если бы атмосфера сконцентрировалась примерно на нижних 9 км.

Если атмосферной рефракцией пренебречь , то из простых геометрических соображений можно показать ( Шенберг 1929 , 173), что путь $s$ светового луча под зенитным углом $z$ через радиально-симметричную атмосферу высоты $y_{\mathrm {atm} }$ над Землей определяется выражением $$s={\sqrt {R_{\mathrm {E} }^{2}\cos ^{2}z+2R_{\mathrm {E} }y_{\mathrm {atm} }+y_{\mathrm {atm} }^{2}}}-R_{\mathrm {E} }\cos \,z\,$$или альтернативно, $$s={\sqrt {\left(R_{\mathrm {E} }+y_{\mathrm {atm} }\right)^{2}-R_{\mathrm {E} }^{2}\sin ^{2}z}}-R_{\mathrm {E} }\cos \,z\,$$где $R_{\mathrm {E} }$ это радиус Земли.

Тогда относительная воздушная масса составит: $$X={\frac {s}{y_{\mathrm {atm} }}}={\frac {R_{\mathrm {E} }}{y_{\mathrm {atm} }}}{\sqrt {\cos ^{2}z+2{\frac {y_{\mathrm {atm} }}{R_{\mathrm {E} }}}+\left({\frac {y_{\mathrm {atm} }}{R_{\mathrm {E} }}}\right)^{2}}}-{\frac {R_{\mathrm {E} }}{y_{\mathrm {atm} }}}\cos \,z\,.$$

Однородная атмосфера

Если атмосфера однородна (т. е. плотность постоянна), высота атмосферы $y_{\mathrm {atm} }$ следует из гидростатических соображений как: $$y_{\mathrm {atm} }={\frac {kT_{0}}{mg}}\,,$$где $k$ — постоянная Больцмана , $T_{0}$ температура на уровне моря, $m$ - молекулярная масса воздуха, а $g$ это ускорение свободного падения. Хотя это то же самое, что и высота по шкале давления изотермической атмосферы , смысл немного другой. В изотермической атмосфере 37% (1/ e ) атмосферы находится выше высоты шкалы давления; в однородной атмосфере нет атмосферы выше атмосферной высоты.

принимая $T_{0}=\mathrm {288.15~K}$, $m=\mathrm {28.9644\times 1.6605\times 10^{-27}~kg}$, и $g=\mathrm {9.80665~m/s^{2}}$ дает $y_{\mathrm {atm} }\approx \mathrm {8435~m}$. Используя средний радиус Земли в 6371 км, воздушная масса на уровне моря на горизонте равна $$X_{\mathrm {horiz} }={\sqrt {1+2{\frac {R_{\mathrm {E} }}{y_{\mathrm {atm} }}}}}\approx 38.87\,.$$

Однородная сферическая модель несколько недооценивает скорость увеличения воздушной массы у горизонта; Разумное общее соответствие значениям, определенным на основе более строгих моделей, можно получить, установив воздушную массу так, чтобы она соответствовала значению при зенитном угле менее 90 °. Уравнение воздушной массы можно переписать, чтобы получить $${\frac {R_{\mathrm {E} }}{y_{\mathrm {atm} }}}={\frac {X^{2}-1}{2\left(1-X\cos z\right)}}\,;$$что соответствует значению Бемпорада в размере 19,787 в $z$ = 88°дает $R_{\mathrm {E} }/y_{\mathrm {atm} }$ ≈ 631,01 и $X_{\mathrm {horiz} }$ ≈ 35,54. С тем же значением для $R_{\mathrm {E} }$ как указано выше, $y_{\mathrm {atm} }$ ≈ 10 096 м.

Хотя однородная атмосфера не является физически реалистичной моделью, такое приближение разумно, если масштабная высота атмосферы мала по сравнению с радиусом планеты. Модель пригодна для использования (т. е. она не расходится и не стремится к нулю) при всех зенитных углах, включая углы более 90 ° (см. § Однородная сферическая атмосфера с приподнятым наблюдателем ). Модель требует сравнительно небольших вычислительных затрат и, если не требуется высокая точность, дает приемлемые результаты. Однако для зенитных углов менее 90° лучшее соответствие принятым значениям воздушной массы можно получить с помощью несколькихинтерполяционных формул.

Атмосфера переменной плотности

В реальной атмосфере плотность не является постоянной (она уменьшается с увеличением высоты над средним уровнем моря . Абсолютная воздушная масса для геометрического пути света, обсуждавшегося выше, для наблюдателя на уровне моря становится $$\sigma =\int _{0}^{y_{\mathrm {atm} }}{\frac {\rho \,\left(R_{\mathrm {E} }+y\right)\mathrm {d} y}{\sqrt {R_{\mathrm {E} }^{2}\cos ^{2}z+2R_{\mathrm {E} }y+y^{2}}}}\,.$$

Изотермическая атмосфера

Обычно используются несколько основных моделей изменения плотности с высотой. Простейшая изотермическая атмосфера дает $$\rho =\rho _{0}e^{-y/H}\,,$$где $\rho _{0}$ плотность на уровне моря и $H$ плотности — высота шкалы . Когда пределы интегрирования равны нулю и бесконечности, результат известен как функция Чепмена . Приближенный результат получается, если отбросить некоторые члены высокого порядка, что дает ( Young 1974 , стр. 147): $$X\approx {\sqrt {\frac {\pi R}{2H}}}\exp {\left({\frac {R\cos ^{2}z}{2H}}\right)}\,\mathrm {erfc} \left({\sqrt {\frac {R\cos ^{2}z}{2H}}}\right)\,.$$

Приблизительную поправку на рефракцию можно сделать, приняв ( Янг 1974 , стр. 147) $$R=7/6\,R_{\mathrm {E} }\,,$$где $R_{\mathrm {E} }$ – физический радиус Земли. На горизонте приближенное уравнение принимает вид $$X_{\mathrm {horiz} }\approx {\sqrt {\frac {\pi R}{2H}}}\,.$$

Используя масштабную высоту 8435 м, средний радиус Земли 6371 км и включая поправку на рефракцию, $$X_{\mathrm {horiz} }\approx 37.20\,.$$

Политропная атмосфера

Предположение о постоянной температуре является упрощенным; более реалистичной моделью является политропная атмосфера, для которой $$T=T_{0}-\alpha y\,,$$где $T_{0}$ температура на уровне моря и $\alpha$ температуры это скорость падения . Плотность как функция высоты равна $$\rho =\rho _{0}\left(1-{\frac {\alpha }{T}}_{0}y\right)^{1/(\kappa -1)}\,,$$где $\kappa$ – показатель политропы (или индекс политропы). Интеграл воздушной массы для политропической модели не поддается решению в замкнутой форме, за исключением зенита, поэтому интегрирование обычно выполняется численно.

Многослойная атмосфера

Атмосфера Земли состоит из нескольких слоев с разными характеристиками температуры и плотности; Общие атмосферные модели включают Международную стандартную атмосферу и Стандартную атмосферу США . Хорошим приближением для многих целей является политропическая тропосфера высотой 11 км с градиентом градиента 6,5 К/км и изотермическая стратосфера бесконечной высоты ( Гарфинкель 1967 ), которая очень близко соответствует первым двум слоям Международной стандартной атмосферы. Если требуется большая точность, можно использовать больше слоев.

Преломляющая радиально-симметричная атмосфера

При учете атмосферной рефракции трассировка лучей становится необходимой ( Кивалов 2007 ), и абсолютный интеграл воздушной массы становится $$\sigma =\int _{r_{\mathrm {obs} }}^{r_{\mathrm {atm} }}{\frac {\rho \,\mathrm {d} r}{\sqrt {1-\left({\frac {n_{\mathrm {obs} }}{n}}{\frac {r_{\mathrm {obs} }}{r}}\right)^{2}\sin ^{2}z}}}\,$$где $n_{\mathrm {obs} }$ - показатель преломления воздуха на высоте наблюдателя $y_{\mathrm {obs} }$ над уровнем моря, $n$ - показатель преломления на высоте $y$ над уровнем моря, $r_{\mathrm {obs} }=R_{\mathrm {E} }+y_{\mathrm {obs} }$, $r=R_{\mathrm {E} }+y$ расстояние от центра Земли до точки на высоте $y$, и $r_{\mathrm {atm} }=R_{\mathrm {E} }+y_{\mathrm {atm} }$ расстояние до верхнего предела атмосферы на высоте $y_{\mathrm {atm} }$. Показатель преломления в единицах плотности обычно с достаточной точностью определяется ( Гарфинкель, 1967 ). соотношением Гладстона-Дейла $${\frac {n-1}{n_{\mathrm {obs} }-1}}={\frac {\rho }{\rho _{\mathrm {obs} }}}\,.$$

Перестановка и подстановка в абсолютный интеграл воздушных масс дает $$\sigma =\int _{r_{\mathrm {obs} }}^{r_{\mathrm {atm} }}{\frac {\rho \,\mathrm {d} r}{\sqrt {1-\left({\frac {n_{\mathrm {obs} }}{1+(n_{\mathrm {obs} }-1)\rho /\rho _{\mathrm {obs} }}}\right)^{2}\left({\frac {r_{\mathrm {obs} }}{r}}\right)^{2}\sin ^{2}z}}}\,.$$

Количество $n_{\mathrm {obs} }-1$ довольно мал; расширяя первый член в скобках, переставляя несколько раз и игнорируя члены в $(n_{\mathrm {obs} }-1)^{2}$ после каждой перестановки дает ( Kasten & Young 1989 ) $$\sigma =\int _{r_{\mathrm {obs} }}^{r_{\mathrm {atm} }}{\frac {\rho \,\mathrm {d} r}{\sqrt {1-\left[1+2(n_{\mathrm {obs} }-1)(1-{\frac {\rho }{\rho _{\mathrm {obs} }}})\right]\left({\frac {r_{\mathrm {obs} }}{r}}\right)^{2}\sin ^{2}z}}}\,.$$

Однородная сферическая атмосфера с приподнятым наблюдателем

Воздушная масса для наблюдателя с высоты в однородной сферической атмосфере

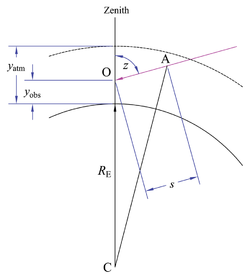
На рисунке справа наблюдатель в точке О находится на высоте $y_{\text{obs}}$ над уровнем моря в однородной радиально-симметричной атмосфере высоты $y_{\mathrm {atm} }$. Длина пути светового луча под зенитным углом $z$ является $s$; $R_{\mathrm {E} }$ это радиус Земли. Применяя закон косинусов к треугольнику ОАС, $${\begin{aligned}\left(R_{E}+y_{\text{atm}}\right)^{2}&=s^{2}+\left(R_{E}+y_{\text{obs}}\right)^{2}-2\left(R_{E}+y_{\text{obs}}\right)s\cos \left(180^{\circ }-z\right)\\&=s^{2}+\left(R_{E}+y_{\text{obs}}\right)^{2}+2\left(R_{E}+y_{\text{obs}}\right)s\cos z\end{aligned}}$$расширяя левую и правую части, устраняя общие члены и переставляя $${{s}^{2}}+2\left({R_{\text{E}}}+{y_{\text{obs}}}\right)s\cos z-2{R_{\text{E}}}{y_{\text{atm}}}-y_{\text{atm}}^{2}+2{R_{\text{E}}}{y_{\text{obs}}}+y_{\text{obs}}^{2}=0\,.$$

Решение квадратичного уравнения для длины пути s , факторизация и перестановка: $$s=\pm {\sqrt {{{\left({R_{\text{E}}}+{y_{\text{obs}}}\right)}^{2}}{{\cos }^{2}}z+2{R_{\text{E}}}\left({y_{\text{atm }}}-{y_{\text{obs}}}\right)+y_{\text{atm}}^{2}-y_{\text{obs}}^{2}}}-({R_{\text{E}}}+{y_{\text{obs}}})\cos z\,.$$

Отрицательный знак радикала дает отрицательный результат, который не имеет физического смысла. Используя положительный знак, разделив на $y_{\mathrm {atm} }$, а отмена общих терминов и перестановка дают относительную воздушную массу: $$X={\sqrt {{{\left({\frac {{R_{\text{E}}}+{y_{\text{obs}}}}{y_{\text{atm}}}}\right)}^{2}}{{\cos }^{2}}z+{\frac {2{R_{\text{E}}}}{y_{\text{atm}}^{2}}}\left({y_{\text{atm}}}-{y_{\text{obs}}}\right)-{{\left({\frac {y_{\text{obs}}}{y_{\text{atm}}}}\right)}^{2}}+1}}-{\frac {{R_{\text{E}}}+{y_{\text{obs}}}}{y_{\text{atm}}}}\cos z\,.$$

С заменами ${\hat {r}}=R_{\mathrm {E} }/y_{\mathrm {atm} }$ и ${\hat {y}}=y_{\mathrm {obs} }/y_{\mathrm {atm} }$, это можно представить как $$X={\sqrt {{({\hat {r}}+{\hat {y}})}^{2}\cos ^{2}z+2{\hat {r}}(1-{\hat {y}})-{\hat {y}}^{2}+1}}\;-\;({\hat {r}}+{\hat {y}})\cos z\,.$$

Когда высота наблюдателя равна нулю, уравнение воздушной массы упрощается до $$X={\sqrt {{{\left({\frac {R_{\text{E}}}{y_{\text{atm}}}}\right)}^{2}}\cos ^{2}z+{\frac {2R_{\text{E}}}{y_{\text{atm}}}}+1}}-{\frac {R_{\text{E}}}{y_{\text{atm}}}}\cos z\,.$$

В пределе пастбищного падения абсолютная воздушная масса равна расстоянию до горизонта . Кроме того, если наблюдатель находится приподнято, зенитный угол горизонта может превышать 90°.

Максимальный зенитный угол для наблюдателя, находящегося на возвышении, в однородной сферической атмосфере

Неравномерное распределение видов-аттенуаторов

Модели атмосферы, основанные на гидростатических соображениях, предполагают наличие атмосферы постоянного состава и единого механизма вымирания, что не совсем верно. Существует три основных источника ослабления ( Hayes & Latham 1975 ): рэлеевское рассеяние на молекулах воздуха, рассеяние Ми на аэрозолях и молекулярное поглощение (в первую очередь озоном ). Относительный вклад каждого источника варьируется в зависимости от высоты над уровнем моря, а концентрации аэрозолей и озона невозможно определить просто из гидростатических соображений.

Строго говоря, когда коэффициент вымирания зависит от высоты, его необходимо определять как часть интеграла воздушной массы, как описано Томасоном, Германом и Рейганом (1983) . Однако зачастую возможен компромиссный подход. Методы отдельного расчета вымирания каждого вида с использованием выражений в закрытой форме описаны в Schaefer (1993) и Schaefer (1998) . Последняя ссылка включает исходный код программы BASIC для выполнения вычислений. Достаточно точный расчет вымирания иногда можно сделать, используя одну из простых формул воздушной массы и отдельно определяя коэффициенты вымирания для каждого из вымирающих видов ( Green 1992 , Pickering 2002 ).

Подразумеваемое

Воздушные массы и астрономия

Пропускание атмосферы в электромагнитном спектре

Смотрите также: Телескоп § Электромагнитная непрозрачность атмосферы

В оптической астрономии воздушная масса является показателем ухудшения наблюдаемого изображения не только в отношении прямых эффектов спектрального поглощения, рассеяния и снижения яркости, но также и совокупности визуальных аберраций , например, возникающих в результате атмосферной турбулентности , которые в совокупности называются как качество « видения ». На более крупных телескопах, таких как WHT ( Wynne & Worswick 1988 ) и VLT ( Avila, Rupprecht & Beckers 1997 ), атмосферная дисперсия может быть настолько серьезной, что влияет на наведение телескопа на цель. В таких случаях используется компенсатор атмосферной дисперсии, который обычно состоит из двух призм.

Частота Гринвуда и параметр Фрида , оба важные для адаптивной оптики , зависят от воздушной массы над ними (точнее, от зенитного угла ).

В радиоастрономии воздушная масса (которая влияет на длину оптического пути) не имеет значения. Нижние слои атмосферы, моделируемые воздушной массой, существенно не препятствуют радиоволнам, которые имеют гораздо более низкую частоту, чем оптические волны. Вместо этого на некоторые радиоволны влияет ионосфера в верхних слоях атмосферы. новых радиотелескопов с синтезом апертуры, Особенно это касается поскольку они «видят» гораздо большую часть неба и, следовательно, ионосферу. Фактически, LOFAR требует явной калибровки этих искажающих эффектов ( ван дер Тол и ван дер Вин 2007 ; де Вос, Ганст и Нейбоер 2009 ), но, с другой стороны, он также может изучать ионосферу, вместо этого измеряя эти искажения ( Тиде 2007 ). .

Воздушные массы и солнечная энергия

Спектр солнечного излучения над атмосферой и на поверхности

Основная статья: Воздушная масса (солнечная энергия)

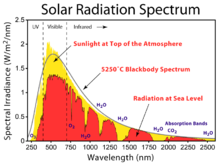
В некоторых областях, таких как солнечная энергетика и фотоэлектрическая энергетика , воздушная масса обозначается аббревиатурой AM; кроме того, значение воздушной массы часто задается путем добавления его значения к AM, так что AM1 указывает воздушную массу 1, AM2 указывает воздушную массу 2 и так далее. Область над атмосферой Земли, где нет атмосферного ослабления солнечной радиации , считается имеющей « нулевую массу воздуха » (AM0).

Ослабление солнечного излучения в атмосфере не одинаково для всех длин волн; следовательно, прохождение через атмосферу не только снижает интенсивность, но и изменяет спектральную освещенность . Фотоэлектрические модули обычно оцениваются по спектральной освещенности для воздушной массы 1,5 (AM1,5); таблицы этих стандартных спектров приведены в ASTM G 173-03 . Внеземное спектральное излучение (т.е. для AM0) приведено в ASTM E 490-00a .

Для многих применений солнечной энергии, когда высокая точность вблизи горизонта не требуется, масса воздуха обычно определяется с использованием простой формулы секущего, описанной в § Плоскопараллельная атмосфера .

См. также

• Воздушная масса (солнечная энергия)
• Атмосферное вымирание
• Закон Бера – Ламберта – Бугера
• Функция Чепмена
• Расчет затухания радиоволн в атмосфере
• Диффузное излучение неба
• Коэффициент вымирания
• Освещенность
• Международная стандартная атмосфера
• Освещенность
• Закон атмосферы
• Рассеяние света
• Рассеяние Ми
• Потеря пути
• Фотоэлектрический модуль
• Рэлеевское рассеяние
• Солнечное облучение

Ссылки

• Аллен, CW (1973). Астрофизические величины (3-е изд.). Лондон: Атлон, 125.: Атлон Пресс. ISBN  0-485-11150-0 . OCLC   952445 . {{cite book}}: CS1 maint: местоположение ( ссылка )
• АСТМ Е 490-00а (Р2006). 2000. Таблицы стандартной солнечной постоянной и спектральной солнечной радиации с нулевой воздушной массой. Вест-Коншохокен, Пенсильвания: ASTM. Доступно для приобретения в ASTM . Оптические телескопы сегодня и завтра
• АСТМ Г 173-03. 2003. Стандартные таблицы для эталонной солнечной спектральной освещенности: прямая нормаль и полусфера на поверхности, наклоненной на 37 °. Вест-Коншохокен, Пенсильвания: ASTM. Доступно для приобретения в ASTM .
• Авила, Херардо; Рупрехт, Геро; Беккерс, Дж. М. (1997). Арне Л. Ардеберг (ред.). «Коррекция атмосферной дисперсии для фокальных редукторов ФОРС на ESO VLT». Оптические телескопы сегодня и завтра . Труды SPIE. 2871 Оптические телескопы сегодняшнего и завтрашнего дня: 1135–1143. Бибкод : 1997SPIE.2871.1135A . дои : 10.1117/12.269000 . S2CID   120965966 .
• Бемпорад А. 1904. К теории затухания света в земной атмосфере. Объявления от Гросс. Гейдельбергская обсерватория № 4, 1–78.
• Гарфинкель, Борис (1967). «Астрономическая рефракция в политропической атмосфере» . Астрономический журнал . 72 : 235–254. Бибкод : 1967AJ.....72..235G . дои : 10.1086/110225 .
• Грин, Дэниел В.Е., 1992. Поправки на величину вымирания в атмосфере . International Comet Quarterly , 14 июля 1992 г., стр. 55–59.
• Харди, Р.Х. 1962. В астрономических методах . Хилтнер, Вашингтон, изд. Чикаго: Издательство Чикагского университета, 184–. LCCN 62009113. Бибкод 1962aste.book.....H .
• Кивалов, Сергей Н. (2007). «Улучшенная модель чисел воздушных масс с трассировкой лучей». Прикладная оптика . 46 (29): 7091–8. Бибкод : 2007ApOpt..46.7091K . дои : 10.1364/AO.46.007091 . ISSN   0003-6935 . ПМИД   17932515 .
• Хейс, Д.С.; Лэтэм, Д.В. (1975). «Повторное обсуждение атмосферного вымирания и абсолютного спектрально-энергетического распределения Веги» . Астрофизический журнал . 197 : 593–601. Бибкод : 1975ApJ...197..593H . дои : 10.1086/153548 . ISSN   0004-637X .
• Яничек, ПМ, и Дж. А. ДеЯнг. 1987. Компьютерные программы для измерения освещенности Солнца и Луны с зависимыми таблицами и диаграммами , Циркуляр Военно-морской обсерватории США № 171. Вашингтон, округ Колумбия: Военно-морская обсерватория США. Бибкод 1987USNOC.171.....J .
• Кастен, Ф.; Янг, AT (1989). «Пересмотренные оптические таблицы масс воздуха и аппроксимационная формула». Прикладная оптика . 28 (22): 4735–4738. Бибкод : 1989ApOpt..28.4735K . дои : 10.1364/AO.28.004735 . ПМИД   20555942 .
• Пикеринг, К.А. (2002). «Южные пределы древнего звездного каталога» (PDF) . ДИО . 12 (1): 20–39.
• Розенберг, Гжегож В. (1966). Сумерки: исследование по оптике атмосферы . Нью-Йорк: Пленум Пресс. ISBN  978-1-4899-6353-6 . LCCN   65011345 . OCLC   1066196615 .
• Шефер, Брэдли Э. (1993). «Астрономия и пределы зрения» . Перспективы в астрономии . 36 (4): 311–361. Бибкод : 1993ВА.....36..311С . дои : 10.1016/0083-6656(93)90113-X .
• Шефер, Б.Е. 1998. До пределов зрения: насколько глубоко вы можете видеть? Sky & Telescope , май 1998 г., стр. 57–60.
• Шенберг, Э. 1929. Теоретическая фотометрия. О затухании света в земной атмосфере. В Справочнике по астрофизике . Том II, первая половина. Берлин: Шпрингер.
• Тиде, Бо (1 декабря 2007 г.). «Нелинейная физика ионосферы и LOIS/LOFAR». Физика плазмы и управляемый термоядерный синтез . 49 (12Б): В103–В107. arXiv : 0707.4506 . Бибкод : 2007PPCF...49..103T . дои : 10.1088/0741-3335/49/12B/S09 . ISSN   0741-3335 . S2CID   18502182 .
• Томасон, LW; Герман, Б.М.; Рейган, Дж. А. (1 июля 1983 г.). «Влияние атмосферных аттенюаторов со структурированным вертикальным распределением на определение воздушных масс и анализ графиков Лэнгли» . Журнал атмосферных наук . 40 (7): 1851–1854. Бибкод : 1983JAtS...40.1851T . doi : 10.1175/1520-0469(1983)040<1851:TEOAAW>2.0.CO;2 . ISSN   0022-4928 .
• ван дер Тол, Себастьян; ван дер Вин, Алле-Ян (2007). «Ионосферная калибровка для радиотелескопа LOFAR» . 2007 Международный симпозиум по сигналам, схемам и системам . Том. 2. стр. 1–4. дои : 10.1109/ISSCS.2007.4292761 . ISBN  978-1-4244-0968-6 .
• де Вос, М.; Гунст, AW; Ниджбоер, Р. (2009). «Телескоп LOFAR: архитектура системы и обработка сигналов» (PDF) . Труды IEEE . 97 (8): 1431–1437. Бибкод : 2009IEEP..97.1431D . дои : 10.1109/JPROC.2009.2020509 . ISSN   0018-9219 . S2CID   4411160 .
• Винн, CG; Уорсвик, СП (1 февраля 1988 г.). «Атмосферная дисперсия в главном фокусе» . Ежемесячные уведомления Королевского астрономического общества . 230 (3): 457–471. Бибкод : 1988MNRAS.230..457W . дои : 10.1093/mnras/230.3.457 . ISSN   0035-8711 .
• Янг, А.Т. 1974. Атмосферное вымирание. Ч. 3.1 в Методах экспериментальной физики , Vol. 12 Астрофизика , Часть А: Оптика и инфракрасное излучение . ред. Н. Карлтон. Нью-Йорк: Академическая пресса. ISBN   0-12-474912-1 .
• Янг, Эндрю Т. (20 февраля 1994 г.). «Воздушная масса и рефракция» . Прикладная оптика . 33 (6): 1108–1110. Бибкод : 1994ApOpt..33.1108Y . дои : 10.1364/AO.33.001108 . ISSN   0003-6935 . ПМИД   20862124 .
• Янг, Эндрю Т.; Ирвин, Уильям М. (1967). «Многоцветная фотоэлектрическая фотометрия ярких планет. I. Программа и методика» . Астрономический журнал . 72 : 945–950. Бибкод : 1967AJ.....72..945Y . дои : 10.1086/110366 .

Внешние ссылки

• Рида Мейера Загружаемый калькулятор воздушной массы , написанный на C (примечания в исходном коде подробно описывают теорию)
• Система астрофизических данных НАСА Источник электронных копий некоторых ссылок.