Периодические точки комплексных квадратичных отображений

В данной статье описаны периодические точки некоторых комплексных квадратичных отображений . Карта — это формула для вычисления значения переменной на основе ее собственного предыдущего значения или значений; квадратичная степени карта — это карта, которая включает предыдущее значение, возведенное в один и два; а комплексная карта — это карта, в которой переменная и параметры являются комплексными числами . Периодическая точка карты — это значение переменной, которое повторяется через интервалы фиксированной длины.

Эти периодические точки играют роль в теориях множеств Фату и Жюлиа .

Определения

Позволять

$f_{c}(z)=z^{2}+c\,$

— комплексное квадратичное отображение , где $z$ и $c$ являются комплексными числами .

Условно говоря, $f_{c}^{(k)}(z)$ это $k$-кратная композиция из $f_{c}$ самого себя (не путать с $k$-я производная от $f_{c}$) — то есть значение после k -й итерации функции $f_{c}.$ Таким образом

$f_{c}^{(k)}(z)=f_{c}(f_{c}^{(k-1)}(z)).$

Периодические точки комплексного квадратичного отображения периода $p$ точки $z$ динамической плоскости такая, что

$f_{c}^{(p)}(z)=z,$

где $p$ — наименьшее целое положительное число , для которого уравнение выполняется при этом z .

Мы можем ввести новую функцию:

$F_{p}(z,f)=f_{c}^{(p)}(z)-z,$

поэтому периодические точки являются нулями функции $F_{p}(z,f)$: точки z, удовлетворяющие

$F_{p}(z,f)=0,$

который является многочленом степени $2^{p}.$

Количество периодических точек

Степень ​ многочлена $F_{p}(z,f)$ описание периодических точек есть $d=2^{p}$ так что это точно $d=2^{p}$ комплексные корни (= периодические точки), учитываемые с кратностью .

Стабильность периодических точек (орбит) – множитель

Индекс устойчивости периодических точек вдоль горизонтальной оси

границы областей плоскости параметров с притягивающей орбитой периодов 1-6

Критическая орбита дискретной динамической системы на основе комплексного квадратичного многочлена . Он имеет тенденцию слабо притягивать фиксированную точку с abs(множителем) = 0,99993612384259.

Множитель ) (или собственное значение, производная $m(f^{p},z_{0})=\lambda$ рациональной карты $f$ повторяемый $p$ раз в циклической точке $z_{0}$ определяется как:

$m(f^{p},z_{0})=\lambda ={\begin{cases}f^{p\prime }(z_{0}),&{\mbox{if }}z_{0}\neq \infty \\{\frac {1}{f^{p\prime }(z_{0})}},&{\mbox{if }}z_{0}=\infty \end{cases}}$

где $f^{p\prime }(z_{0})$ является первой производной от $f^{p}$ относительно $z$ в $z_{0}$.

Поскольку множитель один и тот же во всех периодических точках данной орбиты, он называется множителем периодической орбиты .

Множитель:

• комплексное число;
• инвариант относительно сопряжения любого рационального отображения в его фиксированной точке;
• используется для проверки устойчивости периодических (также фиксированных) точек с индексом устойчивости $abs(\lambda ).\,$

Периодическая точка – это

• привлечение, когда $abs(\lambda )<1;$
  • супер-привлекательно, когда $abs(\lambda )=0;$
  • притягивать, но не сверхпривлекать, когда $0<abs(\lambda )<1;$
• безразличен, когда $abs(\lambda )=1;$
  • рационально безразличен или параболичен, если $\lambda$ является корнем единства ;
  • иррационально безразлично, если $abs(\lambda )=1$ но множитель не является корнем единицы;
• отталкивание, когда $abs(\lambda )>1.$

Периодические точки

• то, что привлекает, всегда есть в наборе Фату ;
• отталкивающие входят в набор Юлии;
• безразличные неподвижные точки могут находиться в одном или другом. Параболическая периодическая точка принадлежит множеству Жюлиа.

Очки периода 1 (фиксированные точки)

Конечные неподвижные точки

Начнем с нахождения всех конечных точек, оставшихся неизмененными одним применением $f$. Это точки, которые удовлетворяют $f_{c}(z)=z$. То есть мы хотим решить

$z^{2}+c=z,\,$

который можно переписать как

$\ z^{2}-z+c=0.$

Поскольку это обыкновенное квадратное уравнение с одним неизвестным, мы можем применить стандартную формулу квадратного решения :

$\alpha _{1}={\frac {1-{\sqrt {1-4c}}}{2}}$ и $\alpha _{2}={\frac {1+{\sqrt {1-4c}}}{2}}.$

Итак, для $c\in \mathbb {C} \setminus \{1/4\}$ у нас есть две конечные неподвижные точки $\alpha _{1}$ и $\alpha _{2}$.

С

$\alpha _{1}={\frac {1}{2}}-m$ и $\alpha _{2}={\frac {1}{2}}+m$ где $m={\frac {\sqrt {1-4c}}{2}},$

у нас есть $\alpha _{1}+\alpha _{2}=1$.

Таким образом, неподвижные точки симметричны относительно $z=1/2$.

На этом изображении показаны фиксированные точки (обе отталкиваются).

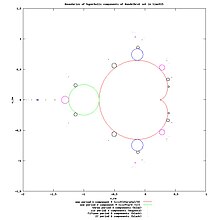
Сложная динамика

Фиксированные точки для c вдоль горизонтальной оси

Набор Фату для F( z ) = z * z с отмеченной неподвижной точкой

Здесь обычно используются другие обозначения:

$\alpha _{c}={\frac {1-{\sqrt {1-4c}}}{2}}$ с множителем $\lambda _{\alpha _{c}}=1-{\sqrt {1-4c}}$

и

$\beta _{c}={\frac {1+{\sqrt {1-4c}}}{2}}$ с множителем $\lambda _{\beta _{c}}=1+{\sqrt {1-4c}}.$

Опять у нас есть

$\alpha _{c}+\beta _{c}=1.$

Поскольку производная по z равна

$P_{c}'(z)={\frac {d}{dz}}P_{c}(z)=2z,$

у нас есть

$P_{c}'(\alpha _{c})+P_{c}'(\beta _{c})=2\alpha _{c}+2\beta _{c}=2(\alpha _{c}+\beta _{c})=2.$

Это подразумевает, что $P_{c}$ может иметь не более одной привлекательной неподвижной точки.

Эти точки отличаются тем, что:

• $\beta _{c}$ является:
  • точка приземления внешнего луча для угла = 0 для $c\in M\setminus \left\{1/4\right\}$
  • самая отталкивающая неподвижная точка множества Жюлиа
  • та, что справа (всякий раз, когда фиксированная точка не симметрична относительно действительной оси ), это крайняя правая точка для связанных множеств Джулии (за исключением цветной капусты).
• $\alpha _{c}$ является:
  • место приземления нескольких лучей
  • привлечение, когда $c$ находится в главной кардиоиде множества Мандельброта, и в этом случае он находится внутри заполненного множества Жюлиа и, следовательно, принадлежит множеству Фату (строго к бассейну притяжения конечной неподвижной точки)
  • параболическая в корневой точке лимба множества Мандельброта
  • отталкивание для других значений $c$

Особые случаи

Важным случаем квадратичного отображения является $c=0$. В этом случае мы получаем $\alpha _{1}=0$ и $\alpha _{2}=1$. В этом случае 0 — это суператтрактивная неподвижная точка , а 1 принадлежит множеству Жюлиа .

Только одна фиксированная точка

У нас есть $\alpha _{1}=\alpha _{2}$ именно когда $1-4c=0.$ Это уравнение имеет одно решение, $c=1/4,$ в этом случае $\alpha _{1}=\alpha _{2}=1/2$. Фактически $c=1/4$ — это наибольшая положительная, чисто действительная величина, для которой существует конечный аттрактор.

Бесконечная фиксированная точка

Мы можем расширить комплексную плоскость $\mathbb {C}$ к сфере Римана (расширенная комплексная плоскость) $\mathbb {\hat {C}}$ добавив бесконечность :

$\mathbb {\hat {C}} =\mathbb {C} \cup \{\infty \}$

и продлить $f_{c}$ такой, что $f_{c}(\infty )=\infty .$

Тогда бесконечность равна:

• суперпривлечение
• фиксированная точка $f_{c}$:
  $$f_{c}(\infty )=\infty =f_{c}^{-1}(\infty ).$$

Циклы периода-2

Бифуркация от периода 1 к периоду 2 для комплексного квадратичного отображения

Бифуркация периодических точек от периода 1 к периоду 2 для fc(z)=z*z +c

Циклы периода 2 — это две разные точки. $\beta _{1}$ и $\beta _{2}$ такой, что $f_{c}(\beta _{1})=\beta _{2}$ и $f_{c}(\beta _{2})=\beta _{1}$, и, следовательно,

$f_{c}(f_{c}(\beta _{n}))=\beta _{n}$

для $n\in \{1,2\}$:

$f_{c}(f_{c}(z))=(z^{2}+c)^{2}+c=z^{4}+2cz^{2}+c^{2}+c.$

Приравнивая это к z , получаем

$z^{4}+2cz^{2}-z+c^{2}+c=0.$

Это уравнение представляет собой полином 4-й степени и поэтому имеет четыре (возможно, неразличимых) решения. Однако мы уже знаем два решения. Они есть $\alpha _{1}$ и $\alpha _{2}$, вычисленное выше, так как если эти точки оставить неизменными одним применением $f$, то, очевидно, они не изменятся при более чем одном применении $f$.

Таким образом, наш полином 4-го порядка можно факторизовать двумя способами:

Первый метод факторизации

$(z-\alpha _{1})(z-\alpha _{2})(z-\beta _{1})(z-\beta _{2})=0.\,$

Это расширяется непосредственно как $x^{4}-Ax^{3}+Bx^{2}-Cx+D=0$ (обратите внимание на чередующиеся знаки), где

$D=\alpha _{1}\alpha _{2}\beta _{1}\beta _{2},\,$

$C=\alpha _{1}\alpha _{2}\beta _{1}+\alpha _{1}\alpha _{2}\beta _{2}+\alpha _{1}\beta _{1}\beta _{2}+\alpha _{2}\beta _{1}\beta _{2},\,$

$B=\alpha _{1}\alpha _{2}+\alpha _{1}\beta _{1}+\alpha _{1}\beta _{2}+\alpha _{2}\beta _{1}+\alpha _{2}\beta _{2}+\beta _{1}\beta _{2},\,$

$A=\alpha _{1}+\alpha _{2}+\beta _{1}+\beta _{2}.\,$

У нас уже есть два решения, и нам нужны только два других. Следовательно, задача эквивалентна решению квадратичного полинома. В частности, отметим, что

$\alpha _{1}+\alpha _{2}={\frac {1-{\sqrt {1-4c}}}{2}}+{\frac {1+{\sqrt {1-4c}}}{2}}={\frac {1+1}{2}}=1$

и

$\alpha _{1}\alpha _{2}={\frac {(1-{\sqrt {1-4c}})(1+{\sqrt {1-4c}})}{4}}={\frac {1^{2}-({\sqrt {1-4c}})^{2}}{4}}={\frac {1-1+4c}{4}}={\frac {4c}{4}}=c.$

Добавляя их к вышесказанному, мы получаем $D=c\beta _{1}\beta _{2}$ и $A=1+\beta _{1}+\beta _{2}$. Сопоставление их с коэффициентами расширения $f$, мы получаем

$D=c\beta _{1}\beta _{2}=c^{2}+c$ и $A=1+\beta _{1}+\beta _{2}=0.$

Отсюда мы легко получаем

$\beta _{1}\beta _{2}=c+1$ и $\beta _{1}+\beta _{2}=-1$.

Отсюда построим квадратное уравнение с $A'=1,B=1,C=c+1$ и примените формулу стандартного решения, чтобы получить

$\beta _{1}={\frac {-1-{\sqrt {-3-4c}}}{2}}$ и $\beta _{2}={\frac {-1+{\sqrt {-3-4c}}}{2}}.$

Более внимательное рассмотрение показывает, что:

$f_{c}(\beta _{1})=\beta _{2}$ и $f_{c}(\beta _{2})=\beta _{1},$

это означает, что эти две точки являются двумя точками одного цикла периода 2.

Второй метод факторизации

Мы можем факторизовать квартику, используя полиномиальное деление в столбик для разделения факторов. $(z-\alpha _{1})$ и $(z-\alpha _{2}),$ которые отвечают за две фиксированные точки $\alpha _{1}$ и $\alpha _{2}$ (значения которых были заданы ранее и которые после двух итераций все еще остаются в фиксированной точке):

$(z^{2}+c)^{2}+c-z=(z^{2}+c-z)(z^{2}+z+c+1).\,$

Корнями первого множителя являются две неподвижные точки. Они отталкиваются за пределами основной кардиоиды.

Второй множитель имеет два корня

${\frac {-1\pm {\sqrt {-3-4c}}}{2}}.\,$

Эти два корня, такие же, как найденные первым методом, образуют орбиту периода 2.

Особые случаи

Опять же, давайте посмотрим на $c=0$. Затем

$\beta _{1}={\frac {-1-i{\sqrt {3}}}{2}}$ и $\beta _{2}={\frac {-1+i{\sqrt {3}}}{2}},$

оба из которых являются комплексными числами. У нас есть $|\beta _{1}|=|\beta _{2}|=1$. Таким образом, обе эти точки «прячутся» в множестве Жюлиа.Другим частным случаем является $c=-1$, что дает $\beta _{1}=0$ и $\beta _{2}=-1$. Это дает хорошо известный суператтрактивный цикл, обнаруженный в самой большой доле периода 2 квадратичного множества Мандельброта.

Циклы для периода больше 2

Периодические точки f ( z ) = z * z −0,75 для периода = 6 как пересечения двух неявных кривых.

Степень уравнения $f^{(n)}(z)=z$ 2 ^н ; так, например, чтобы найти точки на 3-цикле, нам нужно будет решить уравнение 8-й степени. После вычета факторов, дающих две фиксированные точки, мы получим уравнение шестой степени.

Не существует общего решения в радикалах полиномиальных уравнений пятой степени или выше, поэтому точки на цикле с периодом больше 2 обычно должны вычисляться с использованием численных методов . Однако в конкретном случае периода 4 циклические точки имеют длинные выражения в радикалах.

В случае c = –2 тригонометрические решения существуют для периодических точек всех периодов. Дело $z_{n+1}=z_{n}^{2}-2$ эквивалентно логистического отображения случаю r = 4: $x_{n+1}=4x_{n}(1-x_{n}).$ Здесь эквивалентность определяется выражением $z=2-4x.$ Один из k -циклов логистической переменной x (все циклы отталкиваются) равен

$\sin ^{2}\left({\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2\cdot {\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2^{2}\cdot {\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2^{3}\cdot {\frac {2\pi }{2^{k}-1}}\right),\dots ,\sin ^{2}\left(2^{k-1}{\frac {2\pi }{2^{k}-1}}\right).$

Дальнейшее чтение

• Геометрические свойства корней многочленов
• Алан Ф. Бирдон, Итерация рациональных функций, Springer 1991, ISBN   0-387-95151-2
• Майкл Ф. Барнсли (автор), Стивен Г. Демко (редактор), «Хаотическая динамика и фракталы» (серия «Заметки и отчеты по математике в науке и технике») Academic Pr (апрель 1986 г.), ISBN   0-12-079060-2
• Вольф Юнг: Гомеоморфизмы на ребрах множества Мандельброта. доктор философии дипломная работа 2002 г.
• Перестановки периодических точек в квадратных многочленах Дж. Лихи

Внешние ссылки

• Алгебраическое решение границ орбит Мандельброта Дональда Д. Кросса
• Метод Брауна Роберта П. Мунафо
• arXiv:hep-th/0501235v2 В.Долотин, А.Морозов: Алгебраическая геометрия дискретной динамики . Случай одной переменной.