Сила точки

В элементарной плоской геометрии степень точки — это действительное число , которое отражает относительное расстояние данной точки от данной окружности. Он был введен Якобом Штайнером в 1826 году. ^[1]

В частности, власть $\Pi (P)$ точки $P$ относительно круга $c$ с центром $O$ и радиус $r$ определяется

\Pi (P)=|PO|^{2}-r^{2}.

Если $P$ находится вне круга, то $\Pi (P)>0$ ,
если $P$ находится на круге, то $\Pi (P)=0$ и
если $P$ находится внутри круга, то $\Pi (P)<0$ .

По теореме Пифагора число $\Pi (P)$ имеет простой геометрический смысл, показанный на схеме: Для точки $P$ вне круга $\Pi (P)$ квадрат касательного расстояния $|PT|$ точки $P$ в круг $c$ .

равной мощности, изолинии Точки $\Pi (P)$ , являются окружностями, концентрическими окружности $c$ .

Штейнер использовал силу точки для доказательства нескольких утверждений об окружностях, например:

Определение окружности, пересекающей четыре окружности под одним и тем же углом. ^[2]
Решение проблемы Аполлония
Построение кругов Малфатти : ^[3] Для данного треугольника определите три окружности, соприкасающиеся друг с другом и по две стороны треугольника каждая.
Сферическая версия проблемы Малфатти: ^[4] Треугольник имеет сферическую форму.

Важнейшими инструментами исследования окружностей являются радикальная ось двух окружностей и радикальный центр трёх окружностей.

Степенная диаграмма набора кругов делит плоскость на области, внутри которых круг, минимизирующий степень, является постоянным.

В более общем смысле французский математик Эдмон Лагер аналогичным образом определил степень точки по отношению к любой алгебраической кривой.

Геометрические свойства

Помимо свойств, упомянутых в начале, есть и другие свойства:

Ортогональный круг

Для любой точки $P$ за пределами круга $c$ есть две точки касания $T_{1},T_{2}$ по кругу $c$ , которые находятся на равном расстоянии от $P$ . Отсюда и круг $o$ с центром $P$ через $T_{1}$ проходит $T_{2}$ тоже и пересекается $c$ ортогональный:

Круг с центром $P$ и радиус ${\sqrt {\Pi (P)}}$ пересекает круг $c$ ортогональный .

Если радиус $\rho$ круга с центром в $P$ отличается от ${\sqrt {\Pi (P)}}$ получаем угол пересечения $\varphi$ между двумя кругами, применяя закон косинусов (см. схему):

\rho ^{2}+r^{2}-2\rho r\cos \varphi =|PO|^{2}

\rightarrow \ \cos \varphi ={\frac {\rho ^{2}+r^{2}-|PO|^{2}}{2\rho r}}={\frac {\rho ^{2}-\Pi (P)}{2\rho r}}

( $PS_{1}$ и $OS_{1}$ являются нормалями к касательным окружности.)

Если $P$ лежит внутри синего круга, тогда $\Pi (P)<0$ и $\varphi$ всегда отличается от $90^{\circ }$ .

Если угол $\varphi$ задано, то получается радиус $\rho$ решив квадратное уравнение

\rho ^{2}-2\rho r\cos \varphi -\Pi (P)=0

.

Теорема о пересекающихся секущих, теорема о пересекающихся хордах

Для теоремы о пересекающихся секущих и теоремы о хорде степень точки играет роль инварианта :

Теорема о пересекающихся секущих : для точки $P$ вне круга $c$ и точки пересечения $S_{1},S_{2}$ секущей линии $g$ с $c$ верно следующее утверждение: $|PS_{1}|\cdot |PS_{2}|=\Pi (P)$ , следовательно, произведение не зависит от прямой $g$ . Если $g$ касательная тогда $S_{1}=S_{2}$ и это утверждение представляет собой теорему о касательном секущем .
Теорема о пересекающихся хордах : для точки $P$ внутри круга $c$ и точки пересечения $S_{1},S_{2}$ секущей линии $g$ с $c$ верно следующее утверждение: $|PS_{1}|\cdot |PS_{2}|=-\Pi (P)$ , следовательно, произведение не зависит от прямой $g$ .

Радикальная ось

Позволять $P$ быть точкой и $c_{1},c_{2}$ два неконцентрических круга с центры $O_{1},O_{2}$ и радиусы $r_{1},r_{2}$ . Точка $P$ имеет власть $\Pi _{i}(P)$ относительно круга $c_{i}$ . Набор всех точек $P$ с $\Pi _{1}(P)=\Pi _{2}(P)$ представляет собой линию, называемую радикальной осью . Он содержит возможные общие точки окружностей и перпендикулярен прямой. ${\overline {O_{1}O_{2}}}$ .

Теорема о секущих, теорема о хордах: общее доказательство

Обе теоремы, включая теорему о касательном секущем , могут быть доказаны единообразно:

Позволять $P:{\vec {p}}$ быть точкой, $c:{\vec {x}}^{2}-r^{2}=0$ круг с началом координат в центре и ${\vec {v}}$ произвольный единичный вектор . Параметры $t_{1},t_{2}$ возможных общих точек линии $g:{\vec {x}}={\vec {p}}+t{\vec {v}}$ (через $P$ ) и обведите $c$ можно определить, подставив параметрическое уравнение в уравнение окружности:

({\vec {p}}+t{\vec {v}})^{2}-r^{2}=0\quad \rightarrow \quad t^{2}+2t\;{\vec {p}}\cdot {\vec {v}}+{\vec {p}}^{2}-r^{2}=0\ .

Из теоремы Виета можно найти:

t_{1}\cdot t_{2}={\vec {p}}^{2}-r^{2}=\Pi (P)

. (независимо от

{\vec {v}}

)

$\Pi (P)$ это сила $P$ относительно круга $c$ .

Из-за $|{\vec {v}}|=1$ для точек получается следующее утверждение $S_{1},S_{2}$ :

|PS_{1}|\cdot |PS_{2}|=t_{1}t_{2}=\Pi (P)\

, если

P

находится вне круга,

|PS_{1}|\cdot |PS_{2}|=-t_{1}t_{2}=-\Pi (P)\

, если

P

находится внутри круга (

t_{1},t_{2}

имеют разные знаки!).

В случае $t_{1}=t_{2}$ линия $g$ является касательной и $\Pi (P)$ квадрат касательного расстояния до точки $P$ кружить $c$ .

Точки подобия, общая сила двух кругов

Точки сходства

Точки подобия — важный инструмент исследований Штейнера на окружностях. ^[5]

Даны два круга

\ c_{1}:({\vec {x}}-{\vec {m}}_{1})-r_{1}^{2}=0,\quad c_{2}:({\vec {x}}-{\vec {m}}_{2})-r_{2}^{2}=0\ .

Гомотетия ( сходство ) $\sigma$ , это отображает $c_{1}$ на $c_{2}$ радиус растяжения (толчков) $r_{1}$ к $r_{2}$ и имеет свой центр $Z:{\vec {z}}$ на линии ${\overline {M_{1}M_{2}}}$ , потому что $\sigma (M_{1})=M_{2}$ . Если центр $Z$ находится между $M_{1},M_{2}$ масштабный коэффициент $s=-{\tfrac {r_{2}}{r_{1}}}$ . В другом случае $s={\tfrac {r_{2}}{r_{1}}}$ . В любом случае:

\sigma ({\vec {m}}_{1})={\vec {z}}+s({\vec {m}}_{1}-{\vec {z}})={\vec {m}}_{2}

.

Вставка $s=\pm {\tfrac {r_{2}}{r_{1}}}$ и решение для ${\vec {z}}$ дает:

{\vec {z}}={\frac {r_{1}{\vec {m}}_{2}\mp r_{2}{\vec {m}}_{1}}{r_{1}\mp r_{2}}}

.

Точки подобия двух окружностей: различные случаи

Точка $E:{\vec {e}}={\frac {r_{1}{\vec {m}}_{2}-r_{2}{\vec {m}}_{1}}{r_{1}-r_{2}}}$ называется внешней точкой подобия и $I:{\vec {i}}={\frac {r_{1}{\vec {m}}_{2}+r_{2}{\vec {m}}_{1}}{r_{1}+r_{2}}}$ называется внутренней точкой подобия .

В случае $M_{1}=M_{2}$ каждый получает $E=I=M_{i}$ .
В случае $r_{1}=r_{2}$ : $E$ это точка на бесконечности линии ${\overline {M_{1}M_{2}}}$ и $I$ является центром $M_{1},M_{2}$ .
В случае $r_{1}=|EM_{1}|$ круги касаются друг друга в точке $E$ внутри (обе окружности по одну сторону от общей касательной).
В случае $r_{1}=|IM_{1}|$ круги касаются друг друга в точке $I$ снаружи (обе окружности по разные стороны от общей касательной).

Более того:

Если окружности не пересекаются (диски не имеют общих точек), внешние общие касательные пересекаются в точках $E$ и внутренние на $I$ .
Если один круг содержится внутри другого , точки $E,I$ лежат внутри обоих кругов.
Пары $M_{1},M_{2};E,I$ являются проективно-гармоническими сопряжениями : их перекрестное отношение равно $(M_{1},M_{2};E,I)=-1$ .

Теорема Монжа гласит: внешние точки подобия трех непересекающихся окружностей лежат на одной прямой.

Общая сила двух кругов

Точки подобия двух кругов и их общая сила.

Позволять $c_{1},c_{2}$ быть двумя кругами, $E$ их внешняя точка подобия и $g$ линия через $E$ , который пересекает две окружности в четырех точках $G_{1},H_{1},G_{2},H_{2}$ . Из определяющего свойства точки $E$ каждый получает

{\frac {|EG_{1}|}{|EG_{2}|}}={\frac {r_{1}}{r_{2}}}={\frac {|EH_{1}|}{|EH_{2}|}}\

\rightarrow \ |EG_{1}|\cdot |EH_{2}|=|EH_{1}|\cdot |EG_{2}|\

и из теоремы секущего (см. выше) два уравнения

|EG_{1}|\cdot |EH_{1}|=\Pi _{1}(E),\quad |EG_{2}|\cdot |EH_{2}|=\Pi _{2}(E).

Объединение этих трех уравнений дает: ${\begin{aligned}\Pi _{1}(E)\cdot \Pi _{2}(E)&=|EG_{1}|\cdot |EH_{1}|\cdot |EG_{2}|\cdot |EH_{2}|\\&=|EG_{1}|^{2}\cdot |EH_{2}|^{2}=|EG_{2}|^{2}\cdot |EH_{1}|^{2}\ .\end{aligned}}$ Следовательно: $|EG_{1}|\cdot |EH_{2}|=|EG_{2}|\cdot |EH_{1}|={\sqrt {\Pi _{1}(E)\cdot \Pi _{2}(E)}}$ (независимо от линии $g$ !).Аналоговое утверждение для точки внутреннего подобия $I$ это тоже правда.

Инварианты ${\textstyle {\sqrt {\Pi _{1}(E)\cdot \Pi _{2}(E)}},\ {\sqrt {\Pi _{1}(I)\cdot \Pi _{2}(I)}}}$ называются Штейнером общей степенью двух окружностей ( общая мощность двух окружностей относительно их точек подобия ). ^[6]

Пары $G_{1},H_{2}$ и $H_{1},G_{2}$ точек являются антигомологичными точками. Пары $G_{1},G_{2}$ и $H_{1},H_{2}$ гомологичны . ^[7]^[8]

Определение окружности, касающейся двух окружностей

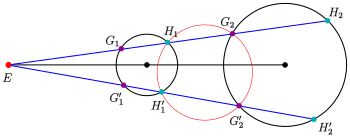
За вторую секущую через $E$ :

|EH_{1}|\cdot |EG_{2}|=|EH'_{1}|\cdot |EG'_{2}|

Из теоремы о секущем получаем:

Четыре пункта

H_{1},G_{2},H'_{1},G'_{2}

лежать на круге.

И аналогично:

Четыре пункта

G_{1},H_{2},G'_{1},H'_{2}

тоже лежать на круге.

Поскольку радикальные линии трех окружностей встречаются в радикале (см.: радикальная линия статьи), получается:

Осушители

{\overline {H_{1}H'_{1}}},\;{\overline {G_{2}G'_{2}}}

встречаются на радикальной оси данных двух окружностей.

При перемещении нижней секущей (см. схему) к верхней красный круг становится окружностью, касающейся обеих данных окружностей. Центр касательной окружности является точкой пересечения прямых. ${\overline {M_{1}H_{1}}},{\overline {M_{2}G_{2}}}$ . Осушители ${\overline {H_{1}H'_{1}}},{\overline {G_{2}G'_{2}}}$ становятся касательными в точках $H_{1},G_{2}$ . Касательные пересекаются на радикальной линии $p$ (на схеме желтый).

Аналогичные соображения порождают вторую касательную окружность, которая пересекает данные окружности в точках $G_{1},H_{2}$ (см. схему).

Все касательные окружности к данным окружностям можно найти, варьируя прямую $g$ .

Позиции центров

Если $X$ является центром и $\rho$ радиус окружности, касающейся данных окружностей в точках $H_{1},G_{2}$ , затем:

\rho =|XM_{1}|-r_{1}=|XM_{2}|-r_{2}

\rightarrow \ |XM_{2}|-|XM_{1}|=r_{2}-r_{1}.

Следовательно: центры лежат на гиперболе с

очаги

M_{1},M_{2}

,

расстояние вершин ^{[ нужны разъяснения ]}

2a=r_{2}-r_{1}

,

центр

M

является центром

M_{1},M_{2}

,

линейный эксцентриситет

c={\tfrac {|M_{1}M_{2}|}{2}}

и

\ b^{2}=e^{2}-a^{2}={\tfrac {|M_{1}M_{2}|^{2}-(r_{2}-r_{1})^{2}}{4}}

^{[ нужны разъяснения ]}.

Рассмотрение внешних касательных окружностей приводит к аналоговому результату:

Если $X$ является центром и $\rho$ радиус окружности, касающейся данных окружностей в точках $G_{1},H_{2}$ , затем:

\rho =|XM_{1}|+r_{1}=|XM_{2}|+r_{2}

\rightarrow \ |XM_{2}|-|XM_{1}|=-(r_{2}-r_{1}).

Центры лежат на той же гиперболе, но на правой ветви.

См. также «Проблему Аполлония» .

Мощность по отношению к сфере

Идею силы точки по отношению к кругу можно распространить на сферу.. ^[9] Теоремы о секущих и хордах верны и для сферы, и их можно доказать буквально, как и в случае с кругом.

Продукт Дарбу

Степень точки — это частный случай произведения Дарбу между двумя окружностями, который определяется выражением ^[10]

\left|A_{1}A_{2}\right|^{2}-r_{1}^{2}-r_{2}^{2}\,

где A ₁ и A ₂ — центры двух окружностей, а r ₁ и r ₂ — их радиусы. Степень точки возникает в том частном случае, когда один из радиусов равен нулю.

Если два круга ортогональны, произведение Дарбу исчезает.

Если два круга пересекаются, то их произведение Дарбу будет

2r_{1}r_{2}\cos \varphi \,

где φ — угол пересечения (см. раздел ортогональная окружность ).

Теорема Лагерра

Лагерр определил степень точки P по отношению к алгебраической кривой степени n как сумму расстояний от точки до пересечений окружности через точку с кривой, деленную на n -ю степень диаметра d. . Лагерр показал, что это число не зависит от диаметра ( Лагерр, 1905 ). В случае, когда алгебраическая кривая представляет собой окружность, это не совсем то же самое, что степень точки относительно окружности, определенная в остальной части статьи, но отличается от нее в d раз. ².

Ссылки

^ Якоб Штайнер: Некоторые геометрические соображения , 1826, стр. 164.
^ Штайнер, с. 163
^ Штайнер, с. 178
^ Штайнер, с. 182
^ Штайнер: с. 170 171
^ Штайнер: с. 175
^ Мишель Шасль, CH Schnuse: Основные положения современной геометрии, первая часть , Verlag Leibrock, Брауншвейг, 1856, с. 312
^ Уильям Дж. Макклелланд: Трактат о геометрии круга и некоторых расширениях конических сечений методом взаимного поступательного движения , 1891, Verlag: Creative Media Partners, LLC, ISBN 978-0-344-90374-8 , с. 121 220
^ КП Гротемейер: Аналитическая геометрия , Göschen Collection 65/65A, Берлин, 1962, стр. 54.
^ Пьер Ларошель, Дж. Майкл Маккарти: Материалы симпозиума USCToMM 2020 г. по механическим системам и робототехнике , 2020, Springer-Verlag, ISBN 978-3-030-43929-3 , с. 97

Коксетер, HSM (1969), Введение в геометрию (2-е изд.), Нью-Йорк: Wiley .
Дарбу, Гастон (1872), «Об отношениях между группами точек, кругов и сфер на плоскости и в пространстве», Annales Scientifiques de l'École Normale Supérieure , 1 : 323–392, doi : 10.24033 / asens.87 .
Лагерр, Эдмон (1905), Работы Лагерра: Геометрия (на французском языке), Gauthier-Villars et fils, стр. 20
Штайнер, Джейкоб (1826). «Некоторые геометрические соображения» . Журнал Крелля (на немецком языке). 1 : 161-184. дои : 10.1515/crll.1826.1.161 . S2CID 122065577 . Рисунки 8–26 .
Бергер , Марсель (1987), Геометрия I , Спрингер , ISBN 978-3-540-11658-5

Дальнейшее чтение

Огилви CS (1990), Экскурсии по геометрии , Dover Publications, стр. 6–23, ISBN 0-486-26530-7
Coxeter HSM , Greitzer SL (1967), Возвращение к геометрии , Вашингтон : MAA , стр. 27–31, 159–160, ISBN 978-0-88385-619-2
Джонсон Р.А. (1960), Расширенная евклидова геометрия: элементарный трактат по геометрии треугольника и круга (перепечатка издания 1929 года под ред. Хоутона Миффлина), Нью-Йорк: Dover Publications, стр. 28–34, ISBN 978-0-486-46237-0

Внешние ссылки

точки сходимости Джейкоб Штайнер и сила
Вайсштейн, Эрик В. «Сила круга» . Математический мир .
Теорема о пересекающихся хордах при разрезании узла
Теорема о пересекающихся хордах с интерактивной анимацией
Теорема о пересекающихся секущих с интерактивной анимацией

[1] Якоб Штайнер: Некоторые геометрические соображения , 1826, стр. 164.

[2] Штайнер, с. 163

[3] Штайнер, с. 178

[4] Штайнер, с. 182

[5] Штайнер: с. 170 171

[6] Штайнер: с. 175

[7] Мишель Шасль, CH Schnuse: Основные положения современной геометрии, первая часть , Verlag Leibrock, Брауншвейг, 1856, с. 312

[8] Уильям Дж. Макклелланд: Трактат о геометрии круга и некоторых расширениях конических сечений методом взаимного поступательного движения , 1891, Verlag: Creative Media Partners, LLC, ISBN 978-0-344-90374-8 , с. 121 220

[9] КП Гротемейер: Аналитическая геометрия , Göschen Collection 65/65A, Берлин, 1962, стр. 54.

[10] Пьер Ларошель, Дж. Майкл Маккарти: Материалы симпозиума USCToMM 2020 г. по механическим системам и робототехнике , 2020, Springer-Verlag, ISBN 978-3-030-43929-3 , с. 97

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]