Периферийная подгруппа
В алгебраической топологии для периферийной подгруппой пары пространство-подпространство X ⊃ Y является некоторая подгруппа фундаментальной группы дополнительного пространства π 1 ( X − Y ). Его класс сопряженности является инвариантом пары ( X , Y ). То есть любой гомеоморфизм ( X , Y ) → ( X ′, Y ′) индуцирует изоморфизм π 1 ( X − Y ) → π 1 ( X ′ − Y ′), переводящий периферийные подгруппы в периферийные подгруппы.
Периферийная подгруппа состоит из петель в X − Y , которые являются периферийными по отношению к Y , то есть остаются «близкими» к Y (кроме случаев перехода к базовой точке и обратно ). Когда указан упорядоченный набор образующих для периферийной подгруппы, подгруппа и генераторы вместе называются периферийной системой для пары ( X , Y ).
Периферийные системы используются в теории узлов как полный алгебраический инвариант узлов. Существует систематический способ выбора генераторов для периферийной подгруппы узла в трехмерном пространстве , такой, что разные типы узлов всегда имеют алгебраически различные периферийные системы. этой ситуации называются долготой и меридианом узла Образующие в .
Полное определение
[ редактировать ]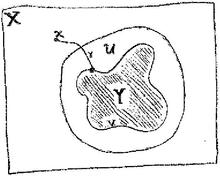
Пусть Y — подпространство линейно связного топологического пространства X , дополнение X − Y которого линейно связно. Зафиксируйте базовую точку x ∈ X − Y . Для каждого компонента пути V i из X − Y ∩ Y выберите путь γ i от x до точки в V i . Элемент [α] ∈ π 1 ( X − Y , x ) называется периферийным относительно этого выбора, если он представлен петлей в U ∪ ∪ i γ i для каждой окрестности U точки Y . Набор всех периферийных элементов относительно данного выбора образует подгруппу π 1 ( X − Y , x ), называемую периферийной подгруппой .
На диаграмме периферийная петля начинается в базовой точке x и движется по пути γ, пока не окажется внутри окрестности U подпространства Y . Тогда он будет перемещаться через U так, как ему нравится (избегая Y ). Наконец, он вернется в базовую точку x через γ. Поскольку U быть очень плотной оболочкой вокруг Y , цикл должен оставаться близко к Y. может
Любые две периферийные подгруппы группы π 1 ( X − Y , x ), возникающие в результате различного выбора путей γ i , сопряжены в π 1 ( X − Y , x ). Кроме того, каждая сопряженная периферийная подгруппа сама является периферийной относительно некоторого выбора путей γi . периферийной подгруппы Таким образом, класс сопряженности является инвариантом пары ( X , Y ).
Периферийная подгруппа вместе с упорядоченным набором образующих называется периферийной системой пары ( X , Y ). Если для выбора этих образующих указан систематический метод, то периферийная система, вообще говоря, является более сильным инвариантом, чем одна периферийная подгруппа. По сути, это полный инвариант узлов.
В теории узлов
[ редактировать ]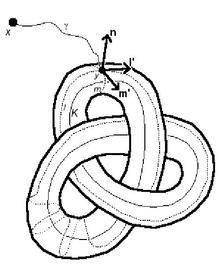
Периферийные подгруппы ручного узла K в R 3 изоморфны Z ⊕ Z, если узел нетривиален, и Z , если это неузел . Они генерируются двумя элементами, называемыми долготой [ l ] и меридианом [ m ]. (Если K — узел, то [ l ] — степень [ m ], а периферийная подгруппа генерируется только [ m ].) Долгота — это петля, которая проходит от базовой точки x по пути γ до точки y на границе трубчатой окрестности K y , затем следует вдоль трубки, делая один полный круг, чтобы вернуться в , затем возвращается в x через γ. Меридиан — это петля, которая проходит от x до y , затем вращается вокруг трубки, возвращается к y , затем возвращается к x . (Свойство быть долготой или меридианом четко определено, поскольку все трубчатые окрестности ручного узла являются изотопными .) Обратите внимание, что каждая группа узлов имеет долготу и меридиан; если [ l ] и [ m ] — долгота и меридиан в данной периферийной подгруппе, то то же самое относится и к [ l ]·[ m ] н и [ м ] −1 соответственно ( n ∈ Z ). Фактически это единственные долготы и меридианы в подгруппе, и любая пара будет порождать подгруппу.
Периферийную систему для узла можно выбрать, выбрав генераторы [ l ] и [ m ] такие, что долгота l имеет номер связи 0 с K , а упорядоченная тройка ( m' , l' , n ) является положительно ориентированным базисом для Р 3 , где m’ — касательный вектор к m , основанный на y , l’ — это касательный вектор l , основанный на y , а n направленная наружу — нормаль, к трубке в точке y . (Предположим, что представители l и m выбраны гладкими на трубке и пересекаются только в точке y .) В этом случае периферийная система является полным инвариантом для узлов, как доказано в [Waldhausen 1968].

Пример: квадратный узел против бабушкиного узла.
[ редактировать ]Квадратный узел и бабушкин узел являются разными узлами и имеют негомеоморфные дополнения . Однако их группы узлов изоморфны. Тем не менее, в [Fox 1961] было показано, что никакой изоморфизм их групп узлов не переводит периферийную подгруппу одного в периферийную подгруппу другого. Таким образом, периферийной подгруппы достаточно, чтобы различить эти узлы.
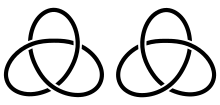
Пример: Трилистник против зеркального трилистника.
[ редактировать ]Трилистник представляют собой разные узлы, и, следовательно , и его зеркальное изображение между их дополнениями нет гомеоморфизма, сохраняющего ориентацию. Однако существует изменяющий ориентацию самогомеоморфизм R 3 который переносит трилистник в его зеркальное отражение. Этот гомеоморфизм индуцирует изоморфизм групп узлов, переводя периферийную подгруппу в периферийную подгруппу, долготу в долготу и меридиан в меридиан. Таким образом, периферийной подгруппы недостаточно, чтобы различить эти узлы. Тем не менее в [Dehn 1914] было показано, что никакой изоморфизм этих групп узлов не сохраняет периферийную систему, выбранную, как описано выше. Изоморфизм в лучшем случае приведет один генератор к генератору, идущему «неправильным путем». Таким образом периферическая система может распознать эти узлы.
Презентация Виртингера
[ редактировать ]можно выразить долготы и меридианы узла словами В виртингеровском представлении группы узлов , без ссылки на сам узел.
Ссылки
[ редактировать ]- Фокс, Ральф Х. , Краткий экскурс в теорию узлов , в: М. К. Форт (ред.), «Топология трехмерных многообразий и смежные темы», Прентис-Холл, Нью-Джерси, 1961, стр. 120–167. МИСТЕР 0140099
- Вальдхаузен, Фридхельм (1968), «О неприводимых трехмерных многообразиях, которые достаточно велики» , Annals of Mathematics , Second Series, 87 (1): 56–88, doi : 10.2307/1970594 , ISSN 0003-486X , JSTOR 1970594 , MR 0224099
- Ден, Макс , Две петли клеверного листа , Mathematical Annals 75 (1914), № 3, 402–413.