Близкие наборы

В математике близкие множества либо пространственно близки , либо дескриптивно близки. Пространственно близкие множества имеют непустое пересечение . Другими словами, пространственно близкие множества не являются непересекающимися множествами , поскольку у них всегда есть хотя бы один общий элемент. Описательно близкие множества содержат элементы, имеющие совпадающие описания. Такие множества могут быть как непересекающимися, так и непересекающимися. Пространственно близкие множества также являются дескриптивно близкими множествами.

В основе описательно близких наборов лежит предположение, что такие наборы содержат элементы, которые имеют местоположение и измеримые характеристики, такие как цвет и частота появления. Описание элемента множества определяется вектором признаков . Сравнение векторов признаков обеспечивает основу для измерения близости описательно близких наборов. Теория близких множеств обеспечивает формальную основу для наблюдения, сравнения и классификации элементов в множествах на основе их близости, как пространственной, так и описательной. Близкие множества предлагают основу для решения проблем, основанных на человеческом восприятии , которые возникают в таких областях, как обработка изображений , компьютерное зрение , а также инженерные и научные проблемы.

Близкие множества имеют множество применений в таких областях, как топология. ^[37], шаблонов обнаружение и классификация ^[50], абстрактная алгебра ^[51], математика в информатике ^[38]и решение множества проблем, основанных на человеческом восприятии ^[42]^[82]^[47]^[52]^[56] которые возникают в таких областях, как анализ изображений ^[54]^[14]^[46]^[17]^[18], обработка изображений ^[40], распознавание лиц ^[13], этология ^[64], а также инженерные и научные проблемы ^[55]^[64]^[42]^[19]^[17]^[18]. С самого начала дескриптивно близкие множества оказались полезными в приложениях топологии. ^[37]и визуальное распознавание образов ^[50], охватывающий широкий спектр приложений, включая обнаружение камуфляжа , микропалеонтологию , обнаружение подделки почерка, анализ биомедицинских изображений, поиск изображений на основе контента , динамику населения , факторную топологию , текстильный дизайн , визуальный мерчендайзинг и топологическую психологию.

В качестве иллюстрации степени описательной близости между двумя наборами рассмотрим пример цветовой модели Генри для различной степени близости.между наборами элементов изображения в изображениях (см., например , ^[17] §4.3). Две пары овалов на рис. 1 и рис. 2 содержат цветные сегменты. Каждый сегмент на рисунках соответствует классу эквивалентности, где все пиксели класса имеют схожие описания, т.е. элементы изображения схожих цветов. Овалы на рис. 1 описательно ближе друг к другу, чем овалы на рис. 2.

История

Было замечено, что простое понятие близости объединяет различные концепции топологических структур. ^[20] поскольку категория Near всех пространств близости и отображений, сохраняющих близость, содержит категории sTop (симметричные топологические пространства и непрерывные отображения ^[3]), Prox ( пространства близости и $\delta$ -карты ^[8]^[67]), Unif ( равномерные пространства и равномерно непрерывные отображения ^[81]^[77]) и Cont (пространства смежности и карты смежности ^[24]) как встроенные полные подкатегории ^[20]^[59]. Категории ${\boldsymbol {\varepsilon {ANear}}}$ и ${\boldsymbol {\varepsilon {AMer}}}$ показаны как полные суперкатегории различных известных категорий, включая категорию ${\boldsymbol {sTop}}$ симметричных топологических пространств и непрерывных отображений, а также категория ${\boldsymbol {Met^{\infty }}}$ расширенных метрических пространств и нерасширяющих отображений. Обозначения ${\boldsymbol {A}}\hookrightarrow {\boldsymbol {B}}$ читает категорию ${\boldsymbol {A}}$ встроен в категорию ${\boldsymbol {B}}$ . Категории ${\boldsymbol {\varepsilon AMer}}$ и ${\boldsymbol {\varepsilon ANear}}$ это суперкатегории для множества знакомых категорий ^[76] показано на рис. 3. Пусть ${\boldsymbol {\varepsilon {ANear}}}$ обозначают категорию всего $\varepsilon$ -приблизиться к пространствам близости и сжатиям и позволить ${\boldsymbol {\varepsilon AMer}}$ обозначают категорию всего $\varepsilon$ -приближение к меротопическим пространствам и сокращениям.

Среди этих знакомых категорий есть ${\boldsymbol {sTop}}$ , симметричная форма ${\boldsymbol {Top}}$ (см. категорию топологических пространств ), категория с объектами, являющимися топологическими пространствами, и морфизмами, являющимися непрерывными отображениями между ними. ^[1]^[32]. ${\boldsymbol {Met^{\infty }}}$ с объектами, являющимися расширенными метрическими пространствами, является подкатегорией ${\boldsymbol {\varepsilon AP}}$ (наличие предметов $\varepsilon$ -приближение к пространствам и сокращениям) (см. также ^[57]^[75]). Позволять $\rho _{X},\rho _{Y}$ быть расширенной псевдометрикой на непустых множествах $X,Y$ , соответственно. Карта $f:(X,\rho _{X})\longrightarrow (Y,\rho _{Y})$ является сокращением тогда и только тогда, когда $f:(X,\nu _{D_{\rho _{X}}})\longrightarrow (Y,\nu _{D_{\rho _{Y}}})$ является сокращением. Для непустых подмножеств $A,B\in 2^{X}$ , функция расстояния $D_{\rho }:2^{X}\times 2^{X}\longrightarrow [0,\infty ]$ определяется

D_{\rho }(A,B)={\begin{cases}\inf {\{\rho (a,b):a\in A,b\in B\}},&{\text{if }}A{\text{ and }}B{\text{ are not empty}},\\\infty ,&{\text{if }}A{\text{ or }}B{\text{ is empty}}.\end{cases}}

Таким образом ${\boldsymbol {\varepsilon }}$ AP встроен как полная подкатегория в ${\boldsymbol {\varepsilon {ANear}}}$ по функтору $F:{\boldsymbol {\varepsilon {AP}}}\longrightarrow {\boldsymbol {\varepsilon {ANear}}}$ определяется $F((X,\rho ))=(X,\nu _{D_{\rho }})$ и $F(f)=f$ . Затем $f:(X,\rho _{X})\longrightarrow (Y,\rho _{Y})$ является сокращением тогда и только тогда, когда $f:(X,\nu _{D_{\rho _{X}}})\longrightarrow (Y,\nu _{D_{\rho _{Y}}})$ является сокращением. Таким образом ${\boldsymbol {\varepsilon {AP}}}$ встроен как полная подкатегория в ${\boldsymbol {\varepsilon {ANear}}}$ по функтору $F:{\boldsymbol {\varepsilon {AP}}}\longrightarrow {\boldsymbol {\varepsilon {ANear}}}$ определяется $F((X,\rho ))=(X,\nu _{D_{\rho }})$ и $F(f)=f.$ Поскольку категория ${\boldsymbol {Met^{\infty }}}$ расширенных метрических пространств и нерасширяющих отображений является полной подкатегорией ${\boldsymbol {\varepsilon {AP}}}$ , поэтому, ${\boldsymbol {\varepsilon {ANear}}}$ также является полной суперкатегорией ${\boldsymbol {Met^{\infty }}}$ . Категория ${\boldsymbol {\varepsilon {ANear}}}$ это топологическая конструкция ^[76].

Понятия ближнего и дальнего ^[А] в математике можно проследить до работ Иоганна Бенедикта Листинга и Феликса Хаусдорфа . Родственные понятия сходства и подобия восходят к Дж. Х. Пуанкаре , который ввел наборы сходных ощущений (зарождающиеся классы толерантности) для представления результатов экспериментов Г.Т. Фехнера по чувствительности к ощущениям. ^[10] и основу для изучения сходства в репрезентативных пространствах как моделей того, что он назвал физическими континуумами. ^[63]^[60]^[61]. Элементами физического континуума (ПК) являются наборы ощущений. Понятие компьютера и различных репрезентативных пространств (тактильное, зрительное, двигательное) было введено Пуанкаре в статье 1894 года о математическом континууме. ^[63], статья 1895 года о пространстве и геометрии. ^[60] и сборник книг 1902 года о науке и гипотезах. ^[61] с последующим рядом уточнений, например , ^[62]. Статьи 1893 и 1895 годов о континуумах (ч. 1, гл. II), а также о репрезентативных пространствах и геометрии (ч. 2, гл. IV) включены в качестве глав в ^[61]. Позднее Ф. Рисс ввел понятие близости или близости пар множеств на Международном конгрессе математиков (ИКМ) в 1908 г. ^[65].

В 1960-х годах ЕС Зееман ввел пространства допусков при моделировании зрительного восприятия. ^[83]. А.Б. Сосинский наблюдал в 1986 г. ^[71] что основная идея, лежащая в основе теории пространства толерантности, исходит от Пуанкаре, особенно ^[60]. В 2002 году З. Павляк и Дж. Питерс ^[Б] считал неформальный подход к восприятию близости физических объектов, таких как снежинки, который не ограничивался пространственной близостью. В 2006 г. формальный подход к описательной близости объектов рассмотрели Дж. Петерс, А. Скоурон и Я. Степанюк. ^[С] в контексте пространств близости ^[39]^[33]^[35]^[21]. В 2007 году Дж. Питерс представил описательно близкие множества. ^[Д]^[И] с последующим введением допуска вблизи множеств ^[41]^[45]. Недавно изучение дескриптивно близких множеств привело к алгебраическим ^[22]^[51], топологическое пространство и пространство близости ^[37] основы таких наборов.

Близость множеств

Прилагательное «рядом» в контексте близких наборов используется для обозначения того факта, что наблюдаемые различия в значениях признаков отдельных объектов достаточно малы, чтобы их можно былосчитаются неотличимыми, т.е. в пределах некоторой допуска.

Точная идея близости, или «сходства», или «нахождения в пределах допуска» достаточно универсальна, чтобы вполне естественно появиться практически в любой математической ситуации.(см., например , ^[66]). Это особенно естественно в математических приложениях: практические задачи чаще всего имеют дело с приблизительными входными данными и требуют только реальных результатов с допустимым уровнем ошибок. ^[71].

Слова «ближний» и «далекий» используются в повседневной жизни, и это было острое предложение Ф. Рисса. ^[65] чтобы эти интуитивные концепции стали строгими. Он представил концепцию близости пар множеств в ICM в Риме в 1908 году. Эта концепция полезна для упрощения обучения исчислению и углубленному исчислению. Например, переход от интуитивного определения непрерывности функции в точке к ее строгому определению эпсилон-дельта иногда бывает трудно объяснить учителям и понять ученикам. Интуитивно непрерывность можно объяснить с помощью языка близости, т. е . функции $f:\mathbb {R} \rightarrow \mathbb {R}$ непрерывен в точке $c$ , предоставлено баллов $\{x\}$ около $c$ перейти к пунктам $\{f(x)\}$ около $f(c)$ . Используя идею Рисса, это определение можно уточнить и противопоставить ему известное определение. ^[4]^[36].

Обобщение пересечения множеств

С пространственной точки зрения близость (также известная как близость) считается обобщением пересечения множеств . Для непересекающихся множеств форма пересечения множеств близости определяется в терминах набора объектов (извлеченных из непересекающихся множеств), которые имеют сходные характеристики в пределах некоторыхтолерантность (см., например , §3 в ^[80]). Например, овалы на рис. 1 считаются близкими друг к другу, поскольку в этих овалах присутствуют пары классов, отображающих схожие (визуально неразличимые) цвета.

Пространство близости Ефремовича

Позволять $X$ Обозначим метрическое топологическое пространство , наделенное одним или несколькими отношениями близости, и пусть $2^{X}$ обозначают совокупность всех подмножеств $X$ . Коллекция $2^{X}$ называется мощности набором $X$ .

Существует много способов определения близости Ефремовича в топологических пространствах (дискретная близость, стандартная близость, метрическая близость, близость Чеха, близость Александрова и близость Фрейденталя). Подробности см. в § 2, стр. 93–94 в ^[6].Здесь основное внимание уделяется стандартной близости в топологическом пространстве. Для $A,B\subset X$ , $A$ рядом $B$ (обозначается $A\ \delta \ B$ ), при условии, что их замыкания имеют общую точку.

Закрытие подмножества $A\in 2^{X}$ (обозначается ${\mbox{cl}}(A)$ ) — обычное замыкание Куратовского множества ^[Ф], введенный в § 4, с. 20 ^[27], определяется

{\begin{aligned}{\mbox{cl}}(A)&=\left\{x\in X:D(x,A)=0\right\},\ {\mbox{where}}\\D(x,A)&=\inf \left\{d(x,a):a\in A\right\}.\end{aligned}}

Т.е., ${\mbox{cl}}(A)$ это совокупность всех точек $x$ в $X$ которые близки к $A$ ( $D(x,A)$ – расстояние Хаусдорфа (см. § 22, с. 128, в ^[15]) между $x$ и набор $A$ и $d(x,a)=\left|x-a\right|$ (стандартное расстояние)). Стандартное отношение близости определяется формулой

\delta =\left\{(A,B)\in 2^{X}\times 2^{X}:{\mbox{cl}}(A)\ \cap \ {\mbox{cl}}(B)\neq \emptyset \right\}.

Всякий раз, когда устанавливается $A$ и $B$ не имеют общих точек, множества далеки друг от друга (обозначаются $A\ {\underline {\delta }}\ B$ ).

Следующая EF-близость ^[Г] пространственные аксиомы даны Юрием Михайловым Смирновым ^[67] на основе того, что представил Вадим Арсеньевич Ефремович в первой половине 1930-х годов. ^[8]. Позволять $A,B,E\in 2^{X}$ .

ЕСЛИ.1: Если набор $A$ близко к $B$ , затем $B$ близко к $A$ .
ЕСЛИ.2: $A\cup B$ близко к $E$ , тогда и только тогда, когда хотя бы одно из множеств $A$ или $B$ близко к $E$ .
ЕСЛИ.3: Две точки близки тогда и только тогда, когда они являются одной и той же точкой.
ЕСЛИ.4: Все наборы далеки от пустого набора $\emptyset$ .
ЕСЛИ.5: Для любых двух наборов $A$ и $B$ которые находятся далеко друг от друга, существует $C,D\in 2^{X}$ , $C\cup D=X$ , такой, что $A$ далеко от $C$ и $B$ далеко от $D$ ( Ефремович-аксиома ).

Пара $(X,\delta )$ называется пространством EF-близости . В этом контексте пространство — это набор с некоторой дополнительной структурой. С близостью пространства $X$ , структура $X$ индуцируется соотношением EF-близости $\delta$ . В пространстве близости $X$ , закрытие $A$ в $X$ совпадает с пересечением всех замкнутых множеств, содержащих $A$ .

Теорема 1 ^[67]: Закрытие любого набора $A$ в пространстве близости $X$ это набор точек $x\in X$ которые близки к $A$ .

Визуализация EF-аксиомы

Пусть набор $X$ быть представлена точками внутри прямоугольной области на рис. 5. Пусть также $A,B$ быть любыми двумя непересекающимися подмножествами ( т.е. подмножествами, пространственно удаленными друг от друга) в $X$ , как показано на рис. 5. Пусть $C^{c}=X\backslash C$ ( дополнение набора $C$ ). Тогда из аксиомы EF наблюдаем следующее:

{\begin{aligned}A&{}\mathrel {\underline {\delta }} B,\\B&\subset C,\\D&=C^{c},\\X&=D\cup C,\\A&\subset D,\ {\mbox{hence, we can write}}\\A\ {\underline {\delta }}\ B\ &\Rightarrow \ A\ {\underline {\delta }}\ C\ {\mbox{and}}\ B\ {\underline {\delta }}\ D,\ {\mbox{for some}}\ C,D\ {\mbox{in}}\ X{\mbox{ so that }}C\cup D=X.\qquad \blacksquare \end{aligned}}

Описательное пространство близости

Описательно близкие множества были представлены как средство решения задач классификации и распознавания образов, возникающих из-за непересекающихся множеств, похожих друг на друга. ^[44]^[43] Недавно были исследованы связи между близкими множествами в EF-пространствах и близкими множествами в описательных пространствах EF-близости. ^[53]^[48]

Опять же, пусть $X$ — метрическое топологическое пространство и пусть $\Phi =\left\{\phi _{1},\dots ,\phi _{n}\right\}$ набор пробных функций, которые представляют особенности каждого $x\in X$ . Здесь сделано предположение $X$ содержит неабстрактные точки, которые имеют измеримые характеристики, такие как ориентация градиента. Неабстрактная точка имеет местоположение и характеристики, которые можно измерить (см. § 3 в ^[26]).

Функция зонда $\phi :X\rightarrow \mathbb {R}$ представляет собой особенность точки выборки в $X$ . Отображение $\Phi :X\longrightarrow \mathbb {R} ^{n}$ определяется $\Phi (x)=(\phi _{1}(x),\dots ,\phi _{n}(x))$ , где $\mathbb {R} ^{n}$ — n-мерное действительное евклидово векторное пространство . $\Phi (x)$ вектор признаков для $x$ , который дает описание $x\in X$ . Например, это приводит к проксимальному просмотру наборов точек изображения на цифровых изображениях. ^[48]

Чтобы получить дескриптивное отношение близости (обозначаемое $\delta _{\Phi }$ ), сначала выбирают набор пробных функций. Позволять ${\mathcal {Q}}:2^{X}\longrightarrow 2^{R^{n}}$ быть отображением на подмножестве $2^{X}$ в подмножество $2^{R^{n}}$ . Например, пусть $A,B\in 2^{X}$ и ${\mathcal {Q}}(A),{\mathcal {Q}}(B)$ обозначают множества описаний точек в $A,B$ , соответственно. То есть,

{\begin{aligned}{\mathcal {Q}}(A)&=\left\{\Phi (a):a\in A\right\},\\{\mathcal {Q}}(B)&=\left\{\Phi (b):b\in B\right\}.\end{aligned}}

Выражение $A\mathrel {\delta _{\Phi }} B$ читает $A$ описательно близок $B$ . Сходным образом, $A\mathrel {{\underline {\delta }}_{\Phi }} B$ читает $A$ описательно далеко от $B$ . Описательная близость $A$ и $B$ определяется

A\mathrel {\delta _{\Phi }} B\Leftrightarrow {\mathcal {Q}}({\mbox{cl}}(A))\mathrel {\delta } {\mathcal {Q}}({\mbox{cl}}(B))\neq \emptyset .

Описательное пересечение $\mathop {\cap } _{\Phi }$ из $A$ и $B$ определяется

A\mathbin {\mathop {\cap } _{\Phi }} B=\left\{x\in A\cup B:{\mathcal {Q}}(A)\mathrel {\delta } {\mathcal {Q}}(B)\right\}.

То есть, $x\in A\cup B$ находится в $A\mathbin {\mathop {\cap } _{\Phi }} B$ , предоставил $\Phi (x)=\Phi (a)=\Phi (b)$ для некоторых $a\in A,b\in B$ . Обратите внимание, что $A$ и $B$ может быть непересекающимся и все же $A\mathbin {\mathop {\cap } _{\Phi }} B$ может быть непустым.

Описательное отношение близости $\delta _{\Phi }$ определяется

\delta _{\Phi }=\left\{(A,B)\in 2^{X}\times 2^{X}:{\mbox{cl}}(A)\mathbin {\mathop {\cap } _{\Phi }} {\mbox{cl}}(B)\neq \emptyset \right\}.

Всякий раз, когда устанавливается $A$ и $B$ не имеют точек с совпадающими описаниями, множества дескриптивно далеки друг от друга (обозначаются $A\ {\underline {\delta }}_{\Phi }\ B$ ).

Бинарное отношение $\delta _{\Phi }$ является описательной EF-близостью при условии, что для $A,B,E\subset X$ .

dEF.1: Если набор $A$ описательно близко к $B$ , затем $B$ описательно близко к $A$ .
dEF.2: $A\cup B$ описательно близко к $E$ , тогда и только тогда, когда хотя бы одно из множеств $A$ или $B$ описательно близко к $E$ .
dEF.3: Две точки $x,y\in X$ дескриптивно близки тогда и только тогда, когда описание $x$ соответствует описанию $y$ .
dEF.4: Все непустые множества описательно далеки от пустого множества. $\emptyset$ .
dEF.5: Для любых двух наборов $A$ и $B$ которые описательно далеки друг от друга, существуют $C,D\in 2^{X}$ , $C\cup D=X$ , такой, что $A$ описательно далеко от $C$ и $B$ описательно далеко от $D$ ( Описательная аксиома Ефремовича ).

Пара $(X,\delta _{\Phi })$ называется дескриптивным пространством близости.

Проксимальные реляционные пространства

Релятор . – это непустое семейство отношений ${\mathcal {R}}$ на непустом множестве $X$ ^[72]. Пара $(X,{\mathcal {R}})$ (также обозначается $X({\mathcal {R}})$ ) называется пространством отношений. Реляционные пространства являются естественными обобщениями упорядоченных множеств и равномерных пространств. ^[73]^[74] С введением семьи близких отношений ${\mathcal {R}}_{\delta }$ на $X$ , мы получаем проксимальное реляционное пространство $(X,{\mathcal {R}}_{\delta })$ . Для простоты мы рассматриваем только два отношения близости, а именно близость Ефремовича $\delta$ ^[8] и описательная близость $\delta _{\Phi }$ в определении описательного отношения ${\mathcal {R}}_{\delta _{\Phi }}$ . ^[53]^[48] Пара $(X,{\mathcal {R}}_{\delta _{\Phi }})$ называется проксимальным реляторным пространством ^[49]. В этой работе $X$ обозначает метрическое топологическое пространство, наделенное отношениями в проксимальном реляторе. С введением $(X,{\mathcal {R}}_{\delta _{\Phi }})$ , традиционное замыкание подмножества (например, ^[9]^[7]) можно сравнить с более поздним описательным замыканием подмножества.

В проксимальном реляторном пространстве $X$ , описательное замыкание множества $A$ (обозначается ${\mbox{cl}}_{\Phi }(A)$ ) определяется

{\mbox{cl}}_{\Phi }(A)=\left\{x\in X:{\Phi (x)}\mathrel {\delta } {\mathcal {Q}}({\mbox{cl}}(A))\right\}.

То есть, $x\in X$ находится в описательном заключении $A$ , при условии закрытия $\Phi (x)$ и закрытие ${\mathcal {Q}}({\mbox{cl}}(A))$ иметь хотя бы один общий элемент.

Теорема 2 ^[50]: Описательное замыкание любого множества $A$ в описательном пространстве EF-близости $(X,{\mathcal {R}}_{\delta _{\Phi }})$ это набор точек $x\in X$ которые описательно близки к $A$ .

Теорема 3 ^[50]: Куратовский закрытие множества $A$ является подмножеством описательного замыкания $A$ в описательном пространстве EF-близости.

Теорема 4 ^[49]: Позволять $(X,{\mathcal {R}}_{\delta _{\Phi }})$ быть проксимальным реляторным пространством, $A\subset X$ . Затем ${\mbox{cl}}(A)\subseteq {\mbox{cl}}_{\Phi }(A)$ .

Доказательство: Позволять $\Phi (x)\in {\mathcal {Q}}(X\setminus {\mbox{cl}}(A))$ такой, что $\Phi (x)=\Phi (a)$ для некоторых $a\in {\mbox{cl}}A$ . Следовательно, $\Phi (x)\in {\mathcal {Q}}({\mbox{cl}}_{\Phi }(A))$ . Следовательно, ${\mbox{cl}}(A)\subseteq {\mbox{cl}}_{\Phi }(A)$

В проксимальном реляторном пространстве EF-близость $\delta$ приводит к следующим результатам для описательной близости $\delta _{\Phi }$ .

Теорема 5 ^[49]

Позволять

(X,{\mathcal {R}}_{\delta _{\Phi }})

быть проксимальным реляторным пространством,

A,B,C\subset X

. Затем

1°: $A\ \delta \ B\ {\mbox{implies}}\ A\ \delta _{\Phi }\ B$ .
2°: $(A\cup B)\ \delta \ C\ {\mbox{implies}}\ (A\cup B)\ \delta _{\Phi }\ C$ .
3°: ${\mbox{cl}}A\ \delta \ {\mbox{cl}}B\ {\mbox{implies}}\ {\mbox{cl}}A\ \delta _{\Phi }\ {\mbox{cl}}B$ .

Доказательство

1°: $A\ \delta \ B\Leftrightarrow A\cap B\neq \emptyset$ . Для $x\in A\cap B,\Phi (x)\in {\mathcal {Q}}(A)$ и $\Phi (x)\in {\mathcal {Q}}(B)$ . Следовательно, $A\ \delta _{\Phi }\ B$ .
1° ⇒ 2°
3°: ${\mbox{cl}}A\ \delta \ {\mbox{cl}}B$ подразумевает, что ${\mbox{cl}}A$ и ${\mbox{cl}}A$ иметь хотя бы одну общую точку. Следовательно, 1° ⇒ 3°.

$\qquad \blacksquare$

Описательные 𝛿-окружения

**Рисунок 6.** Пример изображения $\delta$ -районы

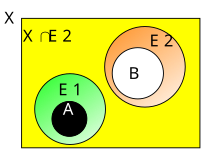
В псевдометрическом проксимальном реляторном пространстве $X$ , окрестность точки $x\in X$ (обозначается $N_{x,\varepsilon }$ ), для $\varepsilon >0$ , определяется

N_{x,\varepsilon }=\left\{y\in X:d(x,y)<\varepsilon \right\}.

Интерьер набора $A$ (обозначается ${\mbox{int}}(A)$ ) и граница $A$ (обозначается ${\mbox{bdy}}(A)$ ) в проксимальном реляторном пространстве $X$ определяются

{\begin{aligned}{\mbox{int}}(A)&=\left\{x\in X:N_{x,\varepsilon }\subseteq A\right\}.\\{\mbox{bdy}}(A)&={\mbox{cl}}(A)\setminus {\mbox{int}}(A).\end{aligned}}

Набор $A$ имеет естественное сильное включение в множество $B$ связанный с $\delta$ ^[5]^[6]} (обозначается $A\ll _{\delta }B$ ), предоставил $A\subset {\mbox{int}}(B)$ ; то есть, $A\mathrel {\underline {\delta }} X\setminus {\mbox{int}}(B)$ ( $A$ далеко не дополняет ${\mbox{int}}(B)$ ). Соответственно, набор $A$ имеет описательное сильное включение в множество $B$ связанный с $\delta _{\Phi }$ (обозначается $A\mathrel {\mathop {\ll } _{\Phi }} B$ ), предоставил ${\mathcal {Q}}(A)\subset \ {\mathcal {Q}}({\mbox{int}}(B))$ ; то есть, $A\ {\underline {\delta }}_{\Phi }\ X\setminus {\mbox{int}}(B)$ ( ${\mathcal {Q}}(A)$ далеко не дополняет ${\mbox{int}}B$ ).

Позволять $\mathop {\ll } _{\Phi }$ быть описательным $\delta$ -отношение соседства, определяемое формулой

\mathop {\ll } _{\Phi }=\left\{(A,B)\in 2^{X}\times 2^{X}:{\mathcal {Q}}(A)\subset {\mathcal {Q}}({\mbox{int}}(B))\right\}.

То есть, $A\mathrel {\mathop {\ll } _{\Phi }} B$ , предоставил описание каждого $a\in A$ содержится в множестве описаний точек $b\in {\mbox{int}}(B)$ . Теперь заметьте, что любой $A,B$ в проксимальном реляторном пространстве $X$ такой, что $A\mathrel {{\underline {\delta }}_{\Phi }} B$ иметь непересекающиеся $\delta _{\Phi }$ -районы; то есть,

A\mathrel {{\underline {\delta }}_{\Phi }} B\Leftrightarrow A\mathrel {\mathop {\ll } _{\Phi }} E1,B\mathrel {\mathop {\ll } _{\Phi }} E2,\ {\mbox{for some}}\ E1,E2\subset X\ {\mbox{(See Fig. 6).}}

Теорема 6 ^[50]: Любые два множества, дескриптивно далекие друг от друга, принадлежат непересекающимся описательным множествам. $\delta _{\Phi }$ -окрестности в описательном пространстве близости $X$ .

Рассмотрение сильной вложенности непустого множества в другое множество приводит к изучению топологий случайных попаданий и топологии Вейсмана. ^[2]

Допуск вблизи множеств

Позволять $\varepsilon$ быть действительным числом, большим нуля. При исследовании множеств, которые проксимально близки в пределах некоторого допуска, набор отношений близости ${\mathcal {R}}_{\delta _{\Phi }}$ дополняется псевдометрическим отношением близости допуска (обозначаемым $\delta _{\Phi ,\varepsilon }$ ) определяется

{\begin{aligned}D_{\Phi }(A,B)&=\inf \left\{d(\Phi (a),\Phi (a)):\Phi (a)\in {\mathcal {Q}}(A),\Phi (a)\in {\mathcal {Q}}(B)\right\},\\d(\Phi (a),\Phi (a))&=\mathop {\sum } _{i=1}^{n}|\phi _{i}(a)-\phi _{i}(b)|,\\\delta _{\Phi ,\varepsilon }&=\left\{(A,B)\in 2^{X}\times 2^{X}:|D({\mbox{cl}}(A),{\mbox{cl}}(B))|<\varepsilon \right\}.\end{aligned}}

Позволять ${\mathcal {R}}_{\delta _{\Phi ,\varepsilon }}={\mathcal {R}}_{\delta _{\Phi }}\cup \left\{\delta _{\Phi ,\varepsilon }\right\}$ . Другими словами, непустое множество, снабженное проксимальным релятором ${\mathcal {R}}_{\delta _{\Phi ,\varepsilon }}$ имеет основную структуру, обеспечиваемую проксимальным релятором ${\mathcal {R}}_{\delta _{\Phi }}$ и обеспечивает основу для изучения толерантности вблизи наборов в $X$ которые находятся в пределах некоторого допуска. Наборы $A,B$ в описательном псевдометрическом проксимальном реляторном пространстве $(X,{\mathcal {R}}_{\delta _{\Phi ,\varepsilon }})$ являются допусками вблизи множеств (т.е. $A\ \delta _{\Phi ,\varepsilon }\ B$ ), предоставил

D_{\Phi }(A,B)<\varepsilon .

Классы толерантности и предварительные классы

Отношения с теми же формальными свойствами, что и отношения подобия ощущений, рассматриваемые Пуанкаре. ^[62] в настоящее время, после Зеемана ^[83], называемые отношениями толерантности . Толерантность  $\tau$ на съемочной площадке $O$ это отношение $\tau \subseteq O\times O$ это рефлексивно и симметрично. В алгебре термин «отношение толерантности» также используется в узком смысле для обозначения рефлексивных и симметричных отношений, определенных в вселенных алгебр, которые также совместимы с операциями данной алгебры, т. е . являются обобщениями отношений конгруэнтности (см ., например , ^[12]). Применительно к таким отношениям термин «алгебраическая толерантность» или термин «алгебраическое отношение толерантности» используется .Транзитивные отношения толерантности являются отношениями эквивалентности. Набор $O$ вместе с толерантностью $\tau$ называется пространством допуска (обозначается $(O,\tau )$ ). Набор $A\subseteq O$ это $\tau$ -preclass (или краткое предварительное классирование , когда $\tau$ понимается) тогда и только тогда, когда для любого $x,y\in A$ , $(x,y)\in \tau$ .

Семейство всех предклассов толерантного пространства естественным образом упорядочивается по включению множества, а предклассы, максимальные по отношению к включению множества, называются $\tau$ -классы или просто занятия , когда $\tau$ понятно. Семья всех классов пространства $(O,\tau )$ особенно интересен и обозначается $H_{\tau }(O)$ . Семья $H_{\tau }(O)$ представляет собой покрытие $O$ ^[58].

Работы Пуанкаре и Зеемана о подобии предвещают появление близких множеств. ^[44]^[43] и исследования отношений сходства, например , ^[79]. В науке и технике допуски вблизи множеств представляют собой практическое применение исследования множеств, близких к некоторым допускам. Толерантность $\varepsilon \in (0,\infty ]$ напрямую связано с идеей близости или сходства ( т. е . нахождения в пределах некоторого допуска) при сравнении объектов.Путем применения подхода Пуанкаре к определению визуальных пространств и подхода Зеемана к отношениям толерантности основная идея состоит в том, чтобы сравнить такие объекты, как участки изображения, внутри цифровых изображений.

Примеры

Простой пример

Следующий простой пример демонстрирует построение классов допусков на основе реальных данных. Рассмотрим 20 объектов в таблице ниже с $|\Phi |=1$ .

Пример системы восприятия
$x_{i}$	$\phi (x)$	$x_{i}$	$\phi (x)$	$x_{i}$	$\phi (x)$	$x_{i}$	$\phi (x)$
$x_{1}$	.4518	$x_{6}$	.6943	$x_{11}$	.4002	$x_{16}$	.6079
$x_{2}$	.9166	$x_{7}$	.9246	$x_{12}$	.1910	$x_{17}$	.1869
$x_{3}$	.1398	$x_{8}$	.3537	$x_{13}$	.7476	$x_{18}$	.8489
$x_{4}$	.7972	$x_{9}$	.4722	$x_{14}$	.4990	$x_{19}$	.9170
$x_{5}$	.6281	$x_{10}$	.4523	$x_{15}$	.6289	$x_{20}$	.7143

Пусть отношение толерантности определяется как

\cong _{\varepsilon }{}\Leftrightarrow \{(x,y)\in O\times O:\;\parallel \Phi (x)-\Phi (y)\parallel _{_{2}}\leq \varepsilon \}

Затем, установив $\varepsilon =0.1$ дает следующие классы допуска:

{\begin{aligned}H_{\cong _{\varepsilon }}(O)={}&\{\{x_{1},x_{8},x_{10},x_{11}\},\{x_{1},x_{9},x_{10},x_{11},x_{14}\},\\&\{x_{2},x_{7},x_{18},x_{19}\},\\&\{x_{3},x_{12},x_{17}\},\\&\{x_{4},x_{13},x_{20}\},\{x_{4},x_{18}\},\\&\{x_{5},x_{6},x_{15},x_{16}\},\{x_{5},x_{6},x_{15},x_{20}\},\\&\{x_{6},x_{13},x_{20}\}\}.\end{aligned}}

Обратите внимание, что каждый объект в классе допуска удовлетворяет условию $\parallel \Phi (x)-\Phi (y)\parallel _{2}\leq \varepsilon$ и что почти все объекты принадлежат более чем одному классу. Более того, если бы использовалось отношение неразличимости, классов было бы двадцать, поскольку не существует двух объектов с совпадающими описаниями.

Пример обработки изображения

**Рисунок 7.** Пример изображений, находящихся рядом друг с другом. (a) и (b) Изображения из свободно доступного набора данных LeavesDataset (см., например, www.vision.caltech.edu/archive.html).

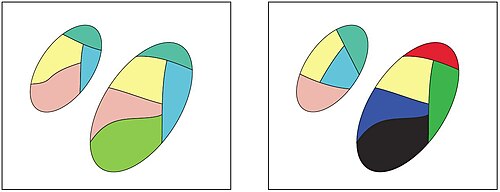
В следующем примере представлен пример, основанный на цифровых изображениях. Пусть фрагмент изображения определяется как небольшое подмножество пикселей, принадлежащих цифровому изображению, такое, что пиксели, содержащиеся в фрагменте изображения, образуют квадрат. Тогда пусть множества $X$ и $Y$ соответственно представляют фрагменты изображений, полученные из двух разных изображений, и пусть $O=\{X\cup Y\}$ . Наконец, пусть описание объекта задается компонентом Green в цветовой модели RGB . Следующий шаг — найти все классы допусков, используя отношение допуска, определенное в предыдущем примере. Используя эту информацию, можно формировать классы допусков, содержащие объекты, имеющие схожие (в пределах некоторых небольших $\varepsilon$ ) значения зеленого компонента в цветовой модели RGB. Кроме того, изображения, близкие (похожие) друг к другу, должны иметь классы допуска, разделенные между обоими изображениями (вместо классов допуска, содержащихся только в одном из изображений). Например, на рисунке, сопровождающем этот пример, показано подмножество классов допуска, полученных из двух изображений листьев. На этом рисунке каждому классу допуска присвоен отдельный цвет. Как можно видеть, оба листа имеют одинаковые классы толерантности. Этот пример подчеркивает необходимость измерения степени близости двух наборов.

Мера близости

Позволять $(U,{\mathcal {R}}_{\delta _{\Phi ,\varepsilon }})$ обозначают конкретное описательное псевдометрическое EF-проксимальное реляционное пространство, снабженное отношением близости $\delta _{\Phi ,\varepsilon }$ и с непустыми подмножествами $X,Y\in 2^{U}$ и с отношением толерантности $\cong _{\Phi ,\varepsilon }$ определяется набором зондов $\Phi$ и с $\varepsilon \in (0,\infty ]$ , где

\simeq _{\Phi ,\varepsilon }=\{(x,y)\in U\times U\mid \ |\Phi (x)-\Phi (y)|\leq \varepsilon \}.

Далее предположим $Z=X\cup Y$ и пусть $H_{\tau _{\Phi ,\varepsilon }}(Z)$ обозначим семейство всех классов в пространстве $(Z,\simeq _{\Phi ,\varepsilon })$ .

Позволять $A\subseteq X,B\subseteq Y$ . Расстояние $D_{_{tNM}}:2^{U}\times 2^{U}:\longrightarrow [0,\infty ]$ определяется

D_{_{tNM}}(X,Y)={\begin{cases}1-tNM(A,B),&{\mbox{if }}X{\mbox{ and }}Y{\mbox{ are not empty}},\\\infty ,&{\mbox{if }}X{\mbox{ or }}Y{\mbox{ is empty}},\end{cases}}

где

tNM(A,B)={\Biggl (}\sum _{C\in H_{\tau _{\Phi ,\varepsilon }}(Z)}|C|{\Biggr )}^{-1}\cdot \sum _{C\in H_{\tau _{\Phi ,\varepsilon }}(Z)}|C|{\frac {\min(|C\cap A|,|[C\cap B|)}{\max(|C\cap A|,|C\cap B|)}}.

Подробности, касающиеся $tNM$ даны в ^[14]^[16]^[17]. Идея, лежащая в основе $tNM$ заключается в том, что подобные наборы должны содержать одинаковое количество объектов в каждом классе допуска. Таким образом, для каждого класса допуска, полученного при покрытии $Z=X\cup Y$ , $tNM$ подсчитывает количество объектов, принадлежащих $X$ и $Y$ и принимает отношение (как правильную дробь) их мощностей. Кроме того, каждое соотношение взвешивается по общему размеру класса допуска (что придает важность более крупным классам), а конечный результат нормализуется путем деления на сумму всех мощностей. Диапазон $tNM$ находится в интервале [0,1], где значение 1 получается, если наборы эквивалентны (на основе описаний объектов), и значение 0 получается, если у них нет общих описаний.

В качестве примера степени близости между двумя наборами рассмотрим рисунок ниже, на котором каждое изображение состоит из двух наборов объектов: $X$ и $Y$ . Каждый цвет на рисунках соответствует множеству, в котором все объекты класса имеют одно и то же описание. Идея, лежащая в основе $tNM$ заключается в том, что близость множеств в системе восприятия основана на количестве классов толерантности, которые они разделяют. Таким образом, множества в левой части рисунка ближе (ближе) друг к другу по своим описаниям, чем множества в правой части рисунка.

Система оценки и распознавания ближней посадки (NEAR)

Система оценки и распознавания ближнего множества (NEAR) - это система, разработанная для демонстрации практического применения теории близкого множества к проблемам оценки сегментации изображений и соответствия изображений. Это было мотивировано необходимостью в свободно доступном программном инструменте, который мог бы предоставить результаты для исследований и вызвать интерес к теории близких множеств. В системе реализован многодокументный интерфейс (MDI), в котором каждая отдельная задача обработки выполняется в своем дочернем фрейме. Объекты (в ближайшем смысле множества) в этой системе представляют собой фрагменты обрабатываемых изображений, а зондовые функции (признаки) — это функции обработки изображений, определенные на фрагментах изображений. Система была написана на C++ и была разработана для облегчения добавления новых задач обработки и функций проверки. В настоящее время система выполняет шесть основных задач, а именно: отображение классов эквивалентности и допуска для изображения, выполнение оценки сегментации, измерение близости двух изображений, выполнение поиска изображений на основе контента (CBIR) и отображение результатов обработки изображения с использованием специальная функция зонда.

Система приближения

Система Proximity — это приложение, разработанное для демонстрации описательных топологических подходов к определению близости и близости в контексте анализа цифровых изображений. Система близости выросла из работ С. Наймпалли и Дж. Питерса о топологических пространствах. Система Proximity написана на Java и предназначена для работы в двух разных операционных средах, а именно на смартфонах и планшетах Android, а также на настольных платформах, на которых работает виртуальная машина Java. Что касается среды рабочего стола, Proximity System представляет собой кроссплатформенное Java-приложение для систем Windows, OSX и Linux, которое было протестировано в Windows 7 и Debian Linux с использованием Sun Java 6 Runtime. С точки зрения реализации теоретических подходов, приложения для Android и настольных компьютеров используют одни и те же серверные библиотеки для выполнения расчетов на основе описаний, причем единственными различиями являются пользовательский интерфейс, а версия Android имеет меньше доступных функций из-за ограничениям на системные ресурсы.

См. также

Примечания

^
Дж. Р. Исбелл заметил, что понятия «ближнее» и «далекое» важны в однородном пространстве. Наборы $A,B$ расположены далеко ( равномерно дистально ) при условии, что $\{A,B\}$ представляет собой дискретную коллекцию. Непустое множество $U$ является однородной окрестностью множества $A$ , при условии дополнения $U$ далеко от $U$ . См. §33 в ^[23]
^
Интуиция, которая привела к открытию описательно близких множеств, описана в работе Павляк З.; Питерс Дж. Ф. (2002, 2007) «Jak blisko (Насколько близко)». Системы Вспомагания Дечизжи I 57 (109)
^
Описательно близкие множества вводятся в ^[48]. Связи между традиционной EF-близостью и описательной EF-близостью исследуются в ^[37].
^
Напоминая подход М. Павла, описания членов объектов-множеств определяются относительно векторов значений, полученных из вещественнозначных функций, называемых зондами. См., Павел М. (1993). Основы распознавания образов . 2-е изд. Нью-Йорк: Марселю Деккеру за введение функций зонда, рассматриваемых в контексте регистрации изображений.
^
Непространственный взгляд на близкие множества появляется в работах К. Дж. Моццочи, М. С. Гаграт и С. А. Наймпалли, Симметричные обобщенные топологические структуры, Exposition Press, Hicksville, NY, 1976, а в последнее время - в близости непересекающихся множеств. $X$ и $Y$ на основе сходства между парами элементов $x\in X,y\in Y$ ( т.е. $x$ и $y$ имеют схожие векторы признаков ${\boldsymbol {\phi (x)}},{\boldsymbol {\phi (y)}}$ и норма $\parallel {\boldsymbol {\phi (x)}}-{\boldsymbol {\phi (y)}}\parallel _{_{p}}<\varepsilon$ ) См., например , ^[43]^[42]^[53].
^
Основные факты о замыкании множества впервые указал М. Фреше в ^[11]и разработан Б. Кнастером и К. Куратовски в ^[25].
^
Заметим, что до 1970-х годов близость означала EF-близость, поскольку именно она интенсивно изучалась. Примером работ по пространствам близости до 1970 г. является серия статей Ю. М. Смирнова в первой половине 1950-х гг. ^[68]^[67]^[69]^[70], кульминацией которого стал обширный сборник результатов С.А. Наймпали и Б.Д. Варрака. ^[34]. Однако, учитывая дальнейшее развитие событий, необходимо различать различные степени близости. Базовая близость или чех-близость была введена Э. Чехом в конце 1930-х годов (см. §25 А.1, стр. 439-440 в ^[78]). Условия несимметричного случая близости были введены С. Лидером. ^[28] и для симметричного случая М.В. Лодато. ^[29]^[30]^[31].

Ссылки

^
Адамек, Дж.; Херрлих, Х.; Стрекер, GE (1990). Абстрактные и конкретные категории . Лондон: Wiley-Interscience. стр. ix+482.
^
Бир, Г. (1993). Топологии на замкнутых и замкнутых выпуклых множествах . Лондон, Великобритания: Академический паб Kluwer.
^
Бентли, ХЛ; Колебандерс, Э.; Вандермиссен, Э. (2009). «Удобная настройка для дополнений и функциональных пространств». В Минарде, Ф.; Перл, Э. (ред.). За пределами топологии . Современная математика. Провиденс, Род-Айленд: Американское математическое общество. стр. 37–88.
^
Кэмерон, П.; Хокинганд, Дж.Г.; Наимпалли, Ю.А. (1974). «Близость – лучший подход к непрерывности и ограничениям». Американский математический ежемесячник . 81 (7): 739–745. дои : 10.2307/2319561 . JSTOR 2319561 .
^
Ди Кончилио, А. (2008). «Действие, единообразие и близость». В Наймпалли, ЮАР; Ди Майо, Г. (ред.). Теория и приложения близости, близости и однородности . Второй университет Неаполя, Неаполь: Прентис-Холл. стр. 71–88.
^ ^{а б}
Ди Кончилио, Анна (2009). «Близость: мощный инструмент в теории расширений, функциональных пространствах, гиперпространствах, булевых алгебрах и бесточечной геометрии». За пределами топологии . Современная математика. Том. 486. Провиденс, Род-Айленд: Американское математическое общество. стр. 89–114. дои : 10.1090/conm/486/09508 . ISBN 9780821842799 . МР 2521943 .
^
Деви, Р.; Сельвакумар, А.; Винешваран, М. (2010). " $(I,\gamma )$ -обобщенные полузамкнутые множества в топологических пространствах». Filomat . 24 (1): 97–100. CiteSeerX 10.1.1.430.5991 . doi : 10.2298/fil1001097d .
^ ^{а б в}
Efremovič, V. A. (1952). "The geometry of proximity I (in Russian)" . Matematicheskii Sbornik . Novaya Seriya. 31(73) (1): 189–200.
^
Питерс, Дж. Ф. (2008). «Заметка об a-открытых множествах и e $^{*}$ -наборы» . Филомат . 22 (1): 89–96. doi : 10.2298/FIL0801087E .
^
Фехнер, GT (1966). Элементы психофизики, вып. Я. Лондон, Великобритания: Холд, Райнхарт и Уинстон. с. Пер. Г. Е. Адлера. Элемента психофизики, 1860 г.
^
Фреше, М. (1906). «О некоторых пунктах функционального исчисления» . Возвращает. Цирк. Мачта. Палермо . 22 :1–74. дои : 10.1007/bf03018603 . hdl : 10338.dmlcz/100655 . S2CID 123251660 .
^
Гретцер, Г.; Венцель, GH (1989). «Допуски, покрывающие системы и аксиома выбора». Архив Математикум . 25 (1–2): 27–34.
^
Гупта, С.; Патнаик, К. (2008). «Повышение производительности систем распознавания лиц за счет использования приближенного подхода к выбору черт лица». Журнал теоретических и прикладных информационных технологий . 4 (5): 433–441.
^ ^{а б}
Хассаниен, А.Е.; Авраам, А.; Питерс, Дж. Ф.; Шефер, Г.; Генри, К. (2009). «Грубые и близкие наборы в медицинской визуализации: обзор». Транзакции IEEE по информационным технологиям в биомедицине . 13 (6): 955–968. CiteSeerX 10.1.1.475.6138 . дои : 10.1109/TITB.2009.2017017 . ПМИД 19304490 . S2CID 1262076 .
^
Хаусдорф, Ф. (1914). Основы теории множеств . Лейпциг: Фейт и компания. стр. VIII + 476.
^
Генри, К.; Питерс, Дж. Ф. (2010). «Международная классификация изображений на основе восприятия». Международный журнал интеллектуальных вычислений и кибернетики . 3 (3): 410–430. дои : 10.1108/17563781011066701 . S2CID 24382697 .
^ ^{а б в г}
Генри, CJ (2010). Близкие множества: Теория и приложения (докторская диссертация). Кафедра электротехники и вычислительной техники Университета Манитобы. hdl : 1993/4267 .
^ ^{а б}
Генри, К.; Питерс, Дж. Ф. (2011). «Измерения сходства движений рук и пальцев при артрите: толерантность при близком к заданному подходе» . Вычислительные и математические методы в медицине . 2011 : 569898. doi : 10.1155/2011/569898 . ПМК 3087412 . ПМИД 21559241 .
^
Генри, CJ; Раманна, С. (2011). «Параллельные вычисления при поиске ближайших окрестностей». Грубые наборы и технология знаний . Конспекты лекций по информатике. Том. 6954. стр. 523–532. дои : 10.1007/978-3-642-24425-4_67 . ISBN 978-3-642-24424-7 .
^ ^{а б}
Херрлих, Х. (1974). «Понятие близости» . Общая топология и ее приложения . 4 (3): 191–212. дои : 10.1016/0016-660x(74)90021-x .
^
Хокинг, Дж. Г.; Наимпали, Ю.А. (2009). «Близость — лучший подход к непрерывности и ограничениям». Однородность и близость . Серия лекций Аллахабадского математического общества. Том. 3. Аллахабад: Аллахабадское математическое общество. стр. iv+66. ISBN 978-81-908159-1-8 .
^
Инан, Э.; Озтюрк, Массачусетс (2012). «Ближайшие группы в пространствах аппроксимации близости». Журнал математики и статистики Хаджеттепе . 41 (4): 545–558.
^
Исбелл, младший (1964). Однородные пространства . Провиденс, Род-Айленд: Американское математическое общество. стр. xi + 175.
^
Иванова, В.М.; Иванов, А.А. (1959). «Пространства смежности и бикомпактные расширения топологических пространств». Докл. Акад. Наук СССР . 127 : 20–22.
^
Кнастер, Б.; Куратовский, К. (1921). «О связных ансамблях» . Основы математики . 2 : 206–255. дои : 10.4064/fm-2-1-206-255 .
^
Ковар, ММ (2011). «Новая причинная топология и почему Вселенная кокомпактна». arXiv : 1112.0817 [ math-ph ].
^
Куратовский, К. (1958). Топологии и . Варшава: Panstwowe Wydawnictwo Naukowe.
^
Лидер, С. (1967). «Метризация пространств близости» . Труды Американского математического общества . 18 (6): 1084–1088. дои : 10.2307/2035803 . JSTOR 2035803 .
^
Лодато, М.В. (1962). О топологически индуцированных обобщенных отношениях близости (докторская диссертация). Университет Рутгерса.
^
Лодато, М.В. (1964). «О топологически индуцированных обобщенных отношениях близости I» . Труды Американского математического общества . 15 (3): 417–422. дои : 10.2307/2034517 . JSTOR 2034517 .
^
Лодато, М.В. (1966). «О топологически индуцированных обобщенных отношениях близости II» . Тихоокеанский математический журнал . 17 : 131–135. дои : 10.2140/pjm.1966.17.131 .
^
Маклейн, С. (1971). Категории для работающего математика . Берлин: Шпрингер. стр. v+262стр.
^
Моццочи, CJ; Наимпали, Ю.А. (2009). «Однородность и близость». Однородность и близость . Серия лекций Аллахабадского математического общества. Том. 2. Аллахабад: Аллахабадское математическое общество. стр. xii+153. ISBN 978-81-908159-1-8 .
^
Наимпалли, Ю.А. (1970). Пространства близости . Кембридж, Великобритания: Издательство Кембриджского университета. стр. х+128. ISBN 978-0-521-09183-1 .
^
Наимпали, Ю.А. (2009). Близкий подход к проблемам топологии и анализа . Мюнхен, Германия: Ольденбург Верлаг. стр. ix + 204. ISBN 978-3-486-58917-7 .
^
Наимпалли, ЮАР; Питерс, Дж. Ф. (2013). «Сохранение преемственности». Японские математические науки . 76 (2): 1–7.
^ ^{а б в г}
Наимпалли, ЮАР; Питерс, Дж. Ф. (2013). Топология с приложениями. Топологические пространства через ближнее и дальнее . Сингапур: World Scientific.
^
Наимпалли, ЮАР; Питерс, Дж. Ф.; Вольский, М. (2013). Теория околомножеств и ее приложения . Специальный выпуск по математике в информатике. Том. 7. Берлин: Шпрингер. п. 136.
^
Наимпалли, ЮАР; Варрак, Б.Д. (1970). Пространства близости . Кембриджские трактаты по математике. Том. 59. Кембридж, Великобритания: Издательство Кембриджского университета.
^
Пал, СК; Питерс, Дж. Ф. (2010). Грубый анализ нечетких изображений. Основы и методологии . Лондон, Великобритания: CRC Press, Taylor & Francisco Group. ISBN 9781439803295 .
^
Питерс, Дж. Ф. (2009). «Допуск вблизи множеств и соответствие изображений». Международный журнал биологических вычислений . 1 (4): 239–245. дои : 10.1504/ijbic.2009.024722 .
^ ^{а б в}
Питерс, Дж. Ф.; Василевский, П. (2009). «Основы близких множеств». Информационные науки . 179 (18): 3091–3109. дои : 10.1016/j.ins.2009.04.018 .
^ ^{а б в}
Питерс, Дж. Ф. (2007). «Ближние множества. Общая теория близости объектов». Прикладные математические науки . 1 (53): 2609–2629.
^ ^{а б}
Питерс, Дж. Ф. (2007). «Ближние множества. Специальная теория близости объектов». Фундамента информатики . 75 (1–4): 407–433.
^
Питерс, Дж. Ф. (2010). «Исправления и дополнения: допуск рядом с наборами и соответствие изображений». Международный журнал биологических вычислений . 2 (5): 310–318. дои : 10.1504/ijbic.2010.036157 .
^
Питерс, Дж. Ф. (2011). «Насколько близки картины Здислава Павляка? Меротопическое расстояние между интересующими регионами». В Сковроне, А.; Сурадж, С. (ред.). Грубые множества и интеллектуальные системы – Памяти профессора Здзислава Павляка . Справочная библиотека интеллектуальных систем. Том. 42. Берлин: Шпрингер. стр. 1–19.
^
Питерс, Дж. Ф. (2011). «Достаточно близко к множеству кварталов». Ин Яо, JT; Раманна, С.; Ван, Г.; Сурадж, З. (ред.). Грубый набор и технология знаний: 6-я Международная конференция, RSKT 2011, Банф, Канада, 9–12 октября 2011 г., Материалы . Конспект лекций по искусственному интеллекту. Том. 6954. Берлин: Шпрингер. стр. 17–24. дои : 10.1007/978-3-642-24425-4_4 .
^ ^{а б в г}
Питерс, Дж. Ф. (2013). «Ближайшие наборы: Введение» . Математика в информатике . 7 (1): 3–9. дои : 10.1007/s11786-013-0149-6 . S2CID 1573876 .
^ ^{а б в}
Питерс, Дж. Ф. (2014). «Проксимальные реляционные пространства». Филомат : 1–5 ( в печати ).
^ ^{а б в г е}
Питерс, Дж. Ф. (2014). Топология цифровых изображений. Визуальное обнаружение закономерностей в пространствах близости . Том. 63. Спрингер. п. 342. ИСБН 978-3-642-53844-5 .
^ ^{а б}
Питерс, Дж. Ф.; Инан, Э.; Озтюрк, Массачусетс (2014). «Пространственные и описательные изометрии в пространствах близости». Общие сведения по математике . 21 (2): 125–134.
^
Питерс, Дж. Ф.; Наимпалли, Ю.А. (2011). «Подходные пространства для близких семей». Общие сведения по математике . 2 (1): 159–164.
^ ^{а б в}
Питерс, Дж. Ф.; Наимпалли, Ю.А. (2011). «Подходы для близких семей» (PDF) . Общие сведения по математике . 2 (1): 159–164.
^
Питерс, Дж. Ф.; Пузио, Л. (2009). «Анализ изображений с использованием мер близости на основе анизотропных вейвлетов». Международный журнал систем вычислительного интеллекта . 2 (3): 168–183. дои : 10.1016/j.ins.2009.04.018 .
^
Питерс, Дж. Ф.; Шахфар, С.; Раманна, С.; Штурм, Т. (2007). «Биологическое адаптивное обучение: почти готовый подход». Границы IEEE в конвергенции бионауки и информационных технологий (FBIT 2007), остров Чеджу, Корея, 11-13 октября 2007 г.
^
Питерс, Дж. Ф.; Тивари, С. (2011). «Подход к меротопии и ближним фильтрам. Теория и применение». Общие сведения по математике . 3 (1): 32–45.
^
Питерс, Дж. Ф.; Тивари, С. (2011). «Подход к меротопии и ближним фильтрам. Теория и применение». Общие сведения по математике . 3 (1): 32–45.
^
Питерс, Дж. Ф.; Василевский, П. (2012). «Пространства толерантности: истоки, теоретические аспекты и приложения». Информационные науки . 195 : 211–225. дои : 10.1016/j.ins.2012.01.023 .
^
Пикадо, Дж. «Пространства близости Вейля». Португальская математика . 55 (2): 233–254.
^ ^{а б в}
Пуанкаре, Дж. Х. (1895). «Пространство и геометрия». Журнал метафизики и морали . 3 (6): 631–646.
^ ^{а б в}
Пуанкаре, Дж. Х. (1902). «На некоторых алгебраических поверхностях; третье дополнение к ситуации анализа» . Бюллетень Математического общества Франции . 30 :49–70. дои : 10.24033/bsmf.657 .
^ ^{а б}
Пуанкаре, Дж. Х. (2009) [1913]. Заключительные мысли, пер. Дж. В. Болдук как Математика и естествознание: Последние очерки . Париж и Нью-Йорк: Фламмарион и Кессинджер.
^ ^{а б}
Пуанкаре, Дж. Х. (1894). «О природе математического рассуждения». Журнал метафизики и морали . 2 (4): 371–384.
^ ^{а б}
Раманна, С.; Мегдади, Ах (2009). «Измерение сходства между поведением стаи: перцепционная толерантность, близкая к установленному подходу». Фундамента информатики . 95 (4): 533–552. дои : 10.3233/FI-2009-163 .
^ ^{а б}
Рисс, Ф. (1908). «Понятие непрерывности и абстрактная теория множеств» (PDF) . Atti del IV Internazionale dei Matematici II : 18–24.
^
Шрейдер, Дж. А. (1975). Равенство, сходство и порядок . Россия: Издательство Мир. п. 279.
^ ^{а б в г}
Smirnov, J. M. (1952). "On proximity spaces" . Matematicheskii Sbornik . Novaya Seriya. 31(73) (3): 543–574. (English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 5–35)
^
Smirnov, J. M. (1952). "On proximity spaces in the sense of V.A. Efremovič". Matematicheskii Sbornik . Novaya Seriya. 84 : 895–898. English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 1–4
^
Смирнов Ю. М. (1954). «О полноте пространств близости. И.». Труды Москов. Мат. Общ . 3 : 271–306, английский перевод: амер. Математика. Соц. Пер. Сер. 2, 38, 1964, 37–74.
^
Смирнов Ю. М. (1955). «О полноте пространств близости. II». Труды Москов. Мат. Общ . 4 : 421–438, английский перевод: амер. Математика. Соц. Пер. Сер. 2, 38, 1964, 75–94.
^ ^{а б}
Сосинский, А.Б. (1986). «Теория пространства толерантности и некоторые приложения». Acta Applicandae Mathematicae . 5 (2): 137–167. дои : 10.1007/bf00046585 . S2CID 119731847 .
^
Саз, А. (1997). «Равномерно, проксимально и топологически компактные реляторы». Математика Панноника . 8 (1): 103–116.
^
Саз, А. (1987). «Основные инструменты и умеренная непрерывность в пространствах отношений» . Acta Mathematica Hungarica . 50 (3–4): 177–201. дои : 10.1007/bf01903935 . S2CID 122231880 .
^
Саз, А (2000). «Распространение теоремы о замкнутом отношении Келли на пространства отношений». Филомат . 14 : 49–71.
^
Тивари, С. (2010). Некоторые аспекты общей топологии и приложений. Подход к меротопическим структурам и приложениям (докторская диссертация). Кафедра математики, Аллахабад (UP), Индия.
^ ^{а б}
Тивари, С.; Питерс, Дж. Ф. (2013). «Новый подход к изучению расширенных метрических пространств». Математика Этерна . 3 (7): 565–577.
^
Тьюки, JW (1940). Сходимость и однородность в топологии . Анналы математических исследований. Том. АМ-2. Принстон, Нью-Джерси: Princeton Univ. Нажимать. п. 90.
^
Чех, Э. (1966). Топологические пространства, перераб. изд. З. Фролик и М. Катетов . Лондон: Джон Уайли и сыновья. п. 893.
^
Василевский, П. (2004). Об избранных отношениях сходства и их применении в когнитивной науке (докторская диссертация). Кафедра логики.
^
Василевский, П.; Питерс, Дж. Ф.; Раманна, С. (2011). «Пересечение перцептивной толерантности». Транзакции с необработанными множествами XIII . Конспекты лекций по информатике. Том. 6499. стр. 159–174. Бибкод : 2011LNCS.6499..159W . дои : 10.1007/978-3-642-18302-7_10 . ISBN 978-3-642-18301-0 .
^
Вейль, А. (1938). О пространствах с однородной структурой и общей топологии . Научные и промышленные новости. Париж: Harmann & ci.
^
Вольски, М. (2010). «Восприятие и классификация. Замечания о близких и грубых множествах». Фундамента информатики . 101 (1–2): 143–155. дои : 10.3233/FI-2010-281 .
^ ^{а б}
Зееман, EC (1962). «Топология мозга и зрительное восприятие». В Форте-младшем, МК (ред.). Топология 3-многообразий и смежные темы . Материалы конференции Института Университета Джорджии. Прентис-Холл. стр. 240–256.

Дальнейшее чтение

Наимпалли, ЮАР; Питерс, Дж. Ф. (2013). Топология с приложениями. Топологические пространства через ближнее и дальнее . Мировое научное издательство. Компания Pte. ООО ISBN 978-981-4407-65-6 .
Наимпалли, ЮАР; Питерс, Дж. Ф.; Вольский, М. (2013). Теория близких множеств и ее приложения . Математика в информатике. Том. 7. Берлин: Шпрингер.
Питерс, Дж. Ф. (2014). Топология цифровых изображений. Визуальное обнаружение закономерностей в пространствах близости . Справочная библиотека интеллектуальных систем. Том. 63. Берлин: Шпрингер.
Генри, CJ; Питерс, Дж. Ф. (2012). Система оценки и распознавания ближнего окружения (NEAR) V3.0 . Технический отчет лаборатории УМ КИ № ТР-2009-015. Лаборатория вычислительного интеллекта Университета Манитобы.
Консилио, А. Ди (2014). Близость: мощный инструмент в теории расширений, функциональных пространствах, гиперпространствах, булевых алгебрах и бесточечной геометрии . Технический отчет лаборатории УМ КИ № ТР-2009-021. Лаборатория вычислительного интеллекта Университета Манитобы.
Питерс, Дж. Ф.; Наимпалли, Ю.А. (2012). «Применение близких множеств» (PDF) . Уведомления Американского математического общества . 59 (4): 536–542. CiteSeerX 10.1.1.371.7903 . дои : 10.1090/noti817 .

[cnote_A_grp_2] 
Дж. Р. Исбелл заметил, что понятия «ближнее» и «далекое» важны в однородном пространстве. Наборы $A,B$ расположены далеко ( равномерно дистально ) при условии, что $\{A,B\}$ представляет собой дискретную коллекцию. Непустое множество $U$ является однородной окрестностью множества $A$ , при условии дополнения $U$ далеко от $U$ . См. §33 в ^[23]

[cnote_B_grp_2] 
Интуиция, которая привела к открытию описательно близких множеств, описана в работе Павляк З.; Питерс Дж. Ф. (2002, 2007) «Jak blisko (Насколько близко)». Системы Вспомагания Дечизжи I 57 (109)

[cnote_C_grp_2] 
Описательно близкие множества вводятся в ^[48]. Связи между традиционной EF-близостью и описательной EF-близостью исследуются в ^[37].

[cnote_D_grp_2] 
Напоминая подход М. Павла, описания членов объектов-множеств определяются относительно векторов значений, полученных из вещественнозначных функций, называемых зондами. См., Павел М. (1993). Основы распознавания образов . 2-е изд. Нью-Йорк: Марселю Деккеру за введение функций зонда, рассматриваемых в контексте регистрации изображений.

[cnote_E_grp_2] 
Непространственный взгляд на близкие множества появляется в работах К. Дж. Моццочи, М. С. Гаграт и С. А. Наймпалли, Симметричные обобщенные топологические структуры, Exposition Press, Hicksville, NY, 1976, а в последнее время - в близости непересекающихся множеств. $X$ и $Y$ на основе сходства между парами элементов $x\in X,y\in Y$ ( т.е. $x$ и $y$ имеют схожие векторы признаков ${\boldsymbol {\phi (x)}},{\boldsymbol {\phi (y)}}$ и норма $\parallel {\boldsymbol {\phi (x)}}-{\boldsymbol {\phi (y)}}\parallel _{_{p}}<\varepsilon$ ) См., например , ^[43]^[42]^[53].

[cnote_F_grp_2] 
Основные факты о замыкании множества впервые указал М. Фреше в ^[11]и разработан Б. Кнастером и К. Куратовски в ^[25].

[cnote_G_grp_2] 
Заметим, что до 1970-х годов близость означала EF-близость, поскольку именно она интенсивно изучалась. Примером работ по пространствам близости до 1970 г. является серия статей Ю. М. Смирнова в первой половине 1950-х гг. ^[68]^[67]^[69]^[70], кульминацией которого стал обширный сборник результатов С.А. Наймпали и Б.Д. Варрака. ^[34]. Однако, учитывая дальнейшее развитие событий, необходимо различать различные степени близости. Базовая близость или чех-близость была введена Э. Чехом в конце 1930-х годов (см. §25 А.1, стр. 439-440 в ^[78]). Условия несимметричного случая близости были введены С. Лидером. ^[28] и для симметричного случая М.В. Лодато. ^[29]^[30]^[31].

[cnote_1] 
Адамек, Дж.; Херрлих, Х.; Стрекер, GE (1990). Абстрактные и конкретные категории . Лондон: Wiley-Interscience. стр. ix+482.

[cnote_2] 
Бир, Г. (1993). Топологии на замкнутых и замкнутых выпуклых множествах . Лондон, Великобритания: Академический паб Kluwer.

[cnote_3] 
Бентли, ХЛ; Колебандерс, Э.; Вандермиссен, Э. (2009). «Удобная настройка для дополнений и функциональных пространств». В Минарде, Ф.; Перл, Э. (ред.). За пределами топологии . Современная математика. Провиденс, Род-Айленд: Американское математическое общество. стр. 37–88.

[cnote_4] 
Кэмерон, П.; Хокинганд, Дж.Г.; Наимпалли, Ю.А. (1974). «Близость – лучший подход к непрерывности и ограничениям». Американский математический ежемесячник . 81 (7): 739–745. дои : 10.2307/2319561 . JSTOR 2319561 .

[cnote_5] 
Ди Кончилио, А. (2008). «Действие, единообразие и близость». В Наймпалли, ЮАР; Ди Майо, Г. (ред.). Теория и приложения близости, близости и однородности . Второй университет Неаполя, Неаполь: Прентис-Холл. стр. 71–88.

[cnote_6] ^{а б}
Ди Кончилио, Анна (2009). «Близость: мощный инструмент в теории расширений, функциональных пространствах, гиперпространствах, булевых алгебрах и бесточечной геометрии». За пределами топологии . Современная математика. Том. 486. Провиденс, Род-Айленд: Американское математическое общество. стр. 89–114. дои : 10.1090/conm/486/09508 . ISBN 9780821842799 . МР 2521943 .

[cnote_7] 
Деви, Р.; Сельвакумар, А.; Винешваран, М. (2010). " $(I,\gamma )$ -обобщенные полузамкнутые множества в топологических пространствах». Filomat . 24 (1): 97–100. CiteSeerX 10.1.1.430.5991 . doi : 10.2298/fil1001097d .

[cnote_8] ^{а б в}
Efremovič, V. A. (1952). "The geometry of proximity I (in Russian)" . Matematicheskii Sbornik . Novaya Seriya. 31(73) (1): 189–200.

[cnote_9] 
Питерс, Дж. Ф. (2008). «Заметка об a-открытых множествах и e $^{*}$ -наборы» . Филомат . 22 (1): 89–96. doi : 10.2298/FIL0801087E .

[cnote_10] 
Фехнер, GT (1966). Элементы психофизики, вып. Я. Лондон, Великобритания: Холд, Райнхарт и Уинстон. с. Пер. Г. Е. Адлера. Элемента психофизики, 1860 г.

[cnote_11] 
Фреше, М. (1906). «О некоторых пунктах функционального исчисления» . Возвращает. Цирк. Мачта. Палермо . 22 :1–74. дои : 10.1007/bf03018603 . hdl : 10338.dmlcz/100655 . S2CID 123251660 .

[cnote_12] 
Гретцер, Г.; Венцель, GH (1989). «Допуски, покрывающие системы и аксиома выбора». Архив Математикум . 25 (1–2): 27–34.

[cnote_13] 
Гупта, С.; Патнаик, К. (2008). «Повышение производительности систем распознавания лиц за счет использования приближенного подхода к выбору черт лица». Журнал теоретических и прикладных информационных технологий . 4 (5): 433–441.

[cnote_14] ^{а б}
Хассаниен, А.Е.; Авраам, А.; Питерс, Дж. Ф.; Шефер, Г.; Генри, К. (2009). «Грубые и близкие наборы в медицинской визуализации: обзор». Транзакции IEEE по информационным технологиям в биомедицине . 13 (6): 955–968. CiteSeerX 10.1.1.475.6138 . дои : 10.1109/TITB.2009.2017017 . ПМИД 19304490 . S2CID 1262076 .

[cnote_15] 
Хаусдорф, Ф. (1914). Основы теории множеств . Лейпциг: Фейт и компания. стр. VIII + 476.

[cnote_16] 
Генри, К.; Питерс, Дж. Ф. (2010). «Международная классификация изображений на основе восприятия». Международный журнал интеллектуальных вычислений и кибернетики . 3 (3): 410–430. дои : 10.1108/17563781011066701 . S2CID 24382697 .

[cnote_17] ^{а б в г}
Генри, CJ (2010). Близкие множества: Теория и приложения (докторская диссертация). Кафедра электротехники и вычислительной техники Университета Манитобы. hdl : 1993/4267 .

[cnote_18] ^{а б}
Генри, К.; Питерс, Дж. Ф. (2011). «Измерения сходства движений рук и пальцев при артрите: толерантность при близком к заданному подходе» . Вычислительные и математические методы в медицине . 2011 : 569898. doi : 10.1155/2011/569898 . ПМК 3087412 . ПМИД 21559241 .

[cnote_19] 
Генри, CJ; Раманна, С. (2011). «Параллельные вычисления при поиске ближайших окрестностей». Грубые наборы и технология знаний . Конспекты лекций по информатике. Том. 6954. стр. 523–532. дои : 10.1007/978-3-642-24425-4_67 . ISBN 978-3-642-24424-7 .

[cnote_20] ^{а б}
Херрлих, Х. (1974). «Понятие близости» . Общая топология и ее приложения . 4 (3): 191–212. дои : 10.1016/0016-660x(74)90021-x .

[cnote_21] 
Хокинг, Дж. Г.; Наимпали, Ю.А. (2009). «Близость — лучший подход к непрерывности и ограничениям». Однородность и близость . Серия лекций Аллахабадского математического общества. Том. 3. Аллахабад: Аллахабадское математическое общество. стр. iv+66. ISBN 978-81-908159-1-8 .

[cnote_22] 
Инан, Э.; Озтюрк, Массачусетс (2012). «Ближайшие группы в пространствах аппроксимации близости». Журнал математики и статистики Хаджеттепе . 41 (4): 545–558.

[cnote_23] 
Исбелл, младший (1964). Однородные пространства . Провиденс, Род-Айленд: Американское математическое общество. стр. xi + 175.

[cnote_24] 
Иванова, В.М.; Иванов, А.А. (1959). «Пространства смежности и бикомпактные расширения топологических пространств». Докл. Акад. Наук СССР . 127 : 20–22.

[cnote_25] 
Кнастер, Б.; Куратовский, К. (1921). «О связных ансамблях» . Основы математики . 2 : 206–255. дои : 10.4064/fm-2-1-206-255 .

[cnote_26] 
Ковар, ММ (2011). «Новая причинная топология и почему Вселенная кокомпактна». arXiv : 1112.0817 [ math-ph ].

[cnote_27] 
Куратовский, К. (1958). Топологии и . Варшава: Panstwowe Wydawnictwo Naukowe.

[cnote_28] 
Лидер, С. (1967). «Метризация пространств близости» . Труды Американского математического общества . 18 (6): 1084–1088. дои : 10.2307/2035803 . JSTOR 2035803 .

[cnote_29] 
Лодато, М.В. (1962). О топологически индуцированных обобщенных отношениях близости (докторская диссертация). Университет Рутгерса.

[cnote_30] 
Лодато, М.В. (1964). «О топологически индуцированных обобщенных отношениях близости I» . Труды Американского математического общества . 15 (3): 417–422. дои : 10.2307/2034517 . JSTOR 2034517 .

[cnote_31] 
Лодато, М.В. (1966). «О топологически индуцированных обобщенных отношениях близости II» . Тихоокеанский математический журнал . 17 : 131–135. дои : 10.2140/pjm.1966.17.131 .

[cnote_32] 
Маклейн, С. (1971). Категории для работающего математика . Берлин: Шпрингер. стр. v+262стр.

[cnote_33] 
Моццочи, CJ; Наимпали, Ю.А. (2009). «Однородность и близость». Однородность и близость . Серия лекций Аллахабадского математического общества. Том. 2. Аллахабад: Аллахабадское математическое общество. стр. xii+153. ISBN 978-81-908159-1-8 .

[cnote_34] 
Наимпалли, Ю.А. (1970). Пространства близости . Кембридж, Великобритания: Издательство Кембриджского университета. стр. х+128. ISBN 978-0-521-09183-1 .

[cnote_35] 
Наимпали, Ю.А. (2009). Близкий подход к проблемам топологии и анализа . Мюнхен, Германия: Ольденбург Верлаг. стр. ix + 204. ISBN 978-3-486-58917-7 .

[cnote_36] 
Наимпалли, ЮАР; Питерс, Дж. Ф. (2013). «Сохранение преемственности». Японские математические науки . 76 (2): 1–7.

[cnote_37] ^{а б в г}
Наимпалли, ЮАР; Питерс, Дж. Ф. (2013). Топология с приложениями. Топологические пространства через ближнее и дальнее . Сингапур: World Scientific.

[cnote_38] 
Наимпалли, ЮАР; Питерс, Дж. Ф.; Вольский, М. (2013). Теория околомножеств и ее приложения . Специальный выпуск по математике в информатике. Том. 7. Берлин: Шпрингер. п. 136.

[cnote_39] 
Наимпалли, ЮАР; Варрак, Б.Д. (1970). Пространства близости . Кембриджские трактаты по математике. Том. 59. Кембридж, Великобритания: Издательство Кембриджского университета.

[cnote_40] 
Пал, СК; Питерс, Дж. Ф. (2010). Грубый анализ нечетких изображений. Основы и методологии . Лондон, Великобритания: CRC Press, Taylor & Francisco Group. ISBN 9781439803295 .

[cnote_41] 
Питерс, Дж. Ф. (2009). «Допуск вблизи множеств и соответствие изображений». Международный журнал биологических вычислений . 1 (4): 239–245. дои : 10.1504/ijbic.2009.024722 .

[cnote_42] ^{а б в}
Питерс, Дж. Ф.; Василевский, П. (2009). «Основы близких множеств». Информационные науки . 179 (18): 3091–3109. дои : 10.1016/j.ins.2009.04.018 .

[cnote_43] ^{а б в}
Питерс, Дж. Ф. (2007). «Ближние множества. Общая теория близости объектов». Прикладные математические науки . 1 (53): 2609–2629.

[cnote_44] ^{а б}
Питерс, Дж. Ф. (2007). «Ближние множества. Специальная теория близости объектов». Фундамента информатики . 75 (1–4): 407–433.

[cnote_45] 
Питерс, Дж. Ф. (2010). «Исправления и дополнения: допуск рядом с наборами и соответствие изображений». Международный журнал биологических вычислений . 2 (5): 310–318. дои : 10.1504/ijbic.2010.036157 .

[cnote_46] 
Питерс, Дж. Ф. (2011). «Насколько близки картины Здислава Павляка? Меротопическое расстояние между интересующими регионами». В Сковроне, А.; Сурадж, С. (ред.). Грубые множества и интеллектуальные системы – Памяти профессора Здзислава Павляка . Справочная библиотека интеллектуальных систем. Том. 42. Берлин: Шпрингер. стр. 1–19.

[cnote_47] 
Питерс, Дж. Ф. (2011). «Достаточно близко к множеству кварталов». Ин Яо, JT; Раманна, С.; Ван, Г.; Сурадж, З. (ред.). Грубый набор и технология знаний: 6-я Международная конференция, RSKT 2011, Банф, Канада, 9–12 октября 2011 г., Материалы . Конспект лекций по искусственному интеллекту. Том. 6954. Берлин: Шпрингер. стр. 17–24. дои : 10.1007/978-3-642-24425-4_4 .

[cnote_48] ^{а б в г}
Питерс, Дж. Ф. (2013). «Ближайшие наборы: Введение» . Математика в информатике . 7 (1): 3–9. дои : 10.1007/s11786-013-0149-6 . S2CID 1573876 .

[cnote_49] ^{а б в}
Питерс, Дж. Ф. (2014). «Проксимальные реляционные пространства». Филомат : 1–5 ( в печати ).

[cnote_50] ^{а б в г е}
Питерс, Дж. Ф. (2014). Топология цифровых изображений. Визуальное обнаружение закономерностей в пространствах близости . Том. 63. Спрингер. п. 342. ИСБН 978-3-642-53844-5 .

[cnote_51] ^{а б}
Питерс, Дж. Ф.; Инан, Э.; Озтюрк, Массачусетс (2014). «Пространственные и описательные изометрии в пространствах близости». Общие сведения по математике . 21 (2): 125–134.

[cnote_52] 
Питерс, Дж. Ф.; Наимпалли, Ю.А. (2011). «Подходные пространства для близких семей». Общие сведения по математике . 2 (1): 159–164.

[cnote_53] ^{а б в}
Питерс, Дж. Ф.; Наимпалли, Ю.А. (2011). «Подходы для близких семей» (PDF) . Общие сведения по математике . 2 (1): 159–164.

[cnote_54] 
Питерс, Дж. Ф.; Пузио, Л. (2009). «Анализ изображений с использованием мер близости на основе анизотропных вейвлетов». Международный журнал систем вычислительного интеллекта . 2 (3): 168–183. дои : 10.1016/j.ins.2009.04.018 .

[cnote_55] 
Питерс, Дж. Ф.; Шахфар, С.; Раманна, С.; Штурм, Т. (2007). «Биологическое адаптивное обучение: почти готовый подход». Границы IEEE в конвергенции бионауки и информационных технологий (FBIT 2007), остров Чеджу, Корея, 11-13 октября 2007 г.

[cnote_56] 
Питерс, Дж. Ф.; Тивари, С. (2011). «Подход к меротопии и ближним фильтрам. Теория и применение». Общие сведения по математике . 3 (1): 32–45.

[cnote_57] 
Питерс, Дж. Ф.; Тивари, С. (2011). «Подход к меротопии и ближним фильтрам. Теория и применение». Общие сведения по математике . 3 (1): 32–45.

[cnote_58] 
Питерс, Дж. Ф.; Василевский, П. (2012). «Пространства толерантности: истоки, теоретические аспекты и приложения». Информационные науки . 195 : 211–225. дои : 10.1016/j.ins.2012.01.023 .

[cnote_59] 
Пикадо, Дж. «Пространства близости Вейля». Португальская математика . 55 (2): 233–254.

[cnote_60] ^{а б в}
Пуанкаре, Дж. Х. (1895). «Пространство и геометрия». Журнал метафизики и морали . 3 (6): 631–646.

[cnote_61] ^{а б в}
Пуанкаре, Дж. Х. (1902). «На некоторых алгебраических поверхностях; третье дополнение к ситуации анализа» . Бюллетень Математического общества Франции . 30 :49–70. дои : 10.24033/bsmf.657 .

[cnote_62] ^{а б}
Пуанкаре, Дж. Х. (2009) [1913]. Заключительные мысли, пер. Дж. В. Болдук как Математика и естествознание: Последние очерки . Париж и Нью-Йорк: Фламмарион и Кессинджер.

[cnote_63] ^{а б}
Пуанкаре, Дж. Х. (1894). «О природе математического рассуждения». Журнал метафизики и морали . 2 (4): 371–384.

[cnote_64] ^{а б}
Раманна, С.; Мегдади, Ах (2009). «Измерение сходства между поведением стаи: перцепционная толерантность, близкая к установленному подходу». Фундамента информатики . 95 (4): 533–552. дои : 10.3233/FI-2009-163 .

[cnote_65] ^{а б}
Рисс, Ф. (1908). «Понятие непрерывности и абстрактная теория множеств» (PDF) . Atti del IV Internazionale dei Matematici II : 18–24.

[cnote_66] 
Шрейдер, Дж. А. (1975). Равенство, сходство и порядок . Россия: Издательство Мир. п. 279.

[cnote_67] ^{а б в г}
Smirnov, J. M. (1952). "On proximity spaces" . Matematicheskii Sbornik . Novaya Seriya. 31(73) (3): 543–574. (English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 5–35)

[cnote_68] 
Smirnov, J. M. (1952). "On proximity spaces in the sense of V.A. Efremovič". Matematicheskii Sbornik . Novaya Seriya. 84 : 895–898. English translation: Amer. Math. Soc. Trans. Ser. 2, 38, 1964, 1–4

[cnote_69] 
Смирнов Ю. М. (1954). «О полноте пространств близости. И.». Труды Москов. Мат. Общ . 3 : 271–306, английский перевод: амер. Математика. Соц. Пер. Сер. 2, 38, 1964, 37–74.

[cnote_70] 
Смирнов Ю. М. (1955). «О полноте пространств близости. II». Труды Москов. Мат. Общ . 4 : 421–438, английский перевод: амер. Математика. Соц. Пер. Сер. 2, 38, 1964, 75–94.

[cnote_71] ^{а б}
Сосинский, А.Б. (1986). «Теория пространства толерантности и некоторые приложения». Acta Applicandae Mathematicae . 5 (2): 137–167. дои : 10.1007/bf00046585 . S2CID 119731847 .

[cnote_72] 
Саз, А. (1997). «Равномерно, проксимально и топологически компактные реляторы». Математика Панноника . 8 (1): 103–116.

[cnote_73] 
Саз, А. (1987). «Основные инструменты и умеренная непрерывность в пространствах отношений» . Acta Mathematica Hungarica . 50 (3–4): 177–201. дои : 10.1007/bf01903935 . S2CID 122231880 .

[cnote_74] 
Саз, А (2000). «Распространение теоремы о замкнутом отношении Келли на пространства отношений». Филомат . 14 : 49–71.

[cnote_75] 
Тивари, С. (2010). Некоторые аспекты общей топологии и приложений. Подход к меротопическим структурам и приложениям (докторская диссертация). Кафедра математики, Аллахабад (UP), Индия.

[cnote_76] ^{а б}
Тивари, С.; Питерс, Дж. Ф. (2013). «Новый подход к изучению расширенных метрических пространств». Математика Этерна . 3 (7): 565–577.

[cnote_77] 
Тьюки, JW (1940). Сходимость и однородность в топологии . Анналы математических исследований. Том. АМ-2. Принстон, Нью-Джерси: Princeton Univ. Нажимать. п. 90.

[cnote_78] 
Чех, Э. (1966). Топологические пространства, перераб. изд. З. Фролик и М. Катетов . Лондон: Джон Уайли и сыновья. п. 893.

[cnote_79] 
Василевский, П. (2004). Об избранных отношениях сходства и их применении в когнитивной науке (докторская диссертация). Кафедра логики.

[cnote_80] 
Василевский, П.; Питерс, Дж. Ф.; Раманна, С. (2011). «Пересечение перцептивной толерантности». Транзакции с необработанными множествами XIII . Конспекты лекций по информатике. Том. 6499. стр. 159–174. Бибкод : 2011LNCS.6499..159W . дои : 10.1007/978-3-642-18302-7_10 . ISBN 978-3-642-18301-0 .

[cnote_81] 
Вейль, А. (1938). О пространствах с однородной структурой и общей топологии . Научные и промышленные новости. Париж: Harmann & ci.

[cnote_82] 
Вольски, М. (2010). «Восприятие и классификация. Замечания о близких и грубых множествах». Фундамента информатики . 101 (1–2): 143–155. дои : 10.3233/FI-2010-281 .

[cnote_83] ^{а б}
Зееман, EC (1962). «Топология мозга и зрительное восприятие». В Форте-младшем, МК (ред.). Топология 3-многообразий и смежные темы . Материалы конференции Института Университета Джорджии. Прентис-Холл. стр. 240–256.

[37]

[50]

[51]

[38]

[42]

[82]

[47]

[52]

[56]

[54]

[14]

[46]

[17]

[18]

[40]

[13]

[64]

[55]

[19]

[20]

[3]

[8]

[67]

[81]

[77]

[24]

[59]

[76]

[1]

[32]

[57]

[75]

[А]

[10]

[63]

[60]

[61]

[62]

[65]

[83]

[71]

[Б]

[С]

[39]

[33]

[35]

[21]

[Д]

[И]

[41]

[45]

[22]

[66]

[4]

[36]

[80]

[6]

[Ф]

[27]

[15]

[Г]

[44]

[43]

[53]

[48]

[26]

[72]

[73]

[74]

[49]

[9]

[7]

[5]

[2]

[12]

[58]

[79]

[16]

[23]

[11]

[25]

[68]

[69]

[70]

[34]

[78]

[28]

[29]

[30]

[31]