Эргодическая гипотеза
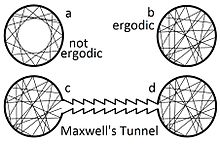

В физике и термодинамике гипотеза эргодическая [1] говорит о том, что в течение длительных периодов времени время пребывания системы в некоторой области фазового пространства микросостояний с одинаковой энергией пропорционально объему этой области, т. е. что все доступные микросостояния равновероятны на протяжении длительного периода времени. время.
Теорема Лиувилля утверждает, что для гамильтоновой системы локальная плотность микросостояний, следующих по пути частицы через фазовое пространство, постоянна с точки зрения наблюдателя, движущегося вместе с ансамблем (т. е. конвективная производная по времени равна нулю). Таким образом, если микросостояния равномерно изначально распределены в фазовом пространстве , они останутся таковыми всегда. Но из теоремы Лиувилля не следует, что эргодическая гипотеза справедлива для всех гамильтоновых систем.
Эргодическая гипотеза часто принимается в статистическом анализе физики вычислительной . Аналитик предполагает, что среднее значение параметра процесса во времени и среднее значение по статистическому ансамблю одинаковы. Это предположение о том, что моделировать систему в течение длительного времени так же хорошо, как и делать множество независимых реализаций одной и той же системы, не всегда верно. (См., например, эксперимент Ферми-Пасты-Улама-Цингу 1953 г.)
Допущение эргодической гипотезы позволяет доказать, что некоторые типы вечных двигателей второго рода невозможны.
Говорят, что эргодические системы обладают свойством эргодичности ; широкий спектр систем в геометрии , физике и теории вероятности являются эргодическими. Эргодические системы изучаются в эргодической теории .
Феноменология
[ редактировать ]В макроскопических системах временные рамки, в течение которых система может действительно исследовать все свое собственное фазовое пространство, могут быть достаточно большими, чтобы состояние термодинамического равновесия демонстрировало некоторую форму нарушения эргодичности . Типичным примером является спонтанная намагниченность в ферромагнитных системах, при которой ниже температуры Кюри система предпочтительно принимает ненулевую намагниченность, хотя эргодическая гипотеза подразумевала бы, что результирующая намагниченность не должна существовать в силу того, что система исследует все состояния, время которых равно нулю. средняя намагниченность должна быть равна нулю. Тот факт, что макроскопические системы часто нарушают буквальную форму эргодической гипотезы, является примером спонтанного нарушения симметрии .
Однако сложные неупорядоченные системы, такие как спиновое стекло, демонстрируют еще более сложную форму нарушения эргодичности, когда свойства состояния термодинамического равновесия, наблюдаемые на практике, гораздо труднее предсказать исключительно на основе аргументов симметрии. Кроме того, обычные стекла (например, оконные) сложным образом нарушают эргодичность. На практике это означает, что в достаточно коротких временных масштабах (например, в доли секунд, минут или несколько часов) системы могут вести себя как твердые тела , т. е. с положительным модулем сдвига, но в чрезвычайно длинных масштабах, например, в течение тысячелетий или эонов. , как жидкости или с двумя или более временными масштабами и плато между ними. [2]
Эргодическая гипотеза в финансах
[ редактировать ]Модели, используемые в финансах и инвестициях , явно или неявно предполагают эргодичность. Эргодическая гипотеза распространена, среди прочего, в современной портфельной теории , моделях дисконтированных денежных потоков (DCF) и совокупных индикаторов моделях , которые лежат в основе макроэкономики .
Ситуации, моделируемые этими теориями, могут быть полезны. Но часто они полезны только в течение большей части изучаемого периода времени, а не всего. Поэтому они могут упустить некоторые из крупнейших отклонений от стандартной модели, такие как финансовые кризисы , долговые кризисы и системные риски в банковской системе, которые происходят нечасто.
Нассим Николас Талеб утверждал, что очень важная часть эмпирической реальности в области финансов и инвестиций неэргодична. Равномерное статистическое распределение вероятностей, при котором система возвращается в каждое возможное состояние бесконечное число раз, просто не тот случай, который мы наблюдаем в ситуациях, когда достигаются «поглощающие состояния», состояния, в которых разрушение наблюдается . Смерть человека, или полная потеря всего, или передача полномочий или расчленение национального государства и правового режима , который сопровождал это, — все это поглощающие государства. Таким образом, в финансах зависимость от пути имеет значение. Путь, на котором человек, фирма или страна натыкается на «стоп» — поглощающий барьер , «все, что мешает людям, имеющим шкуру в игре, выйти из него, и к чему система будет неизменно стремиться. Назовем эти ситуации разорением» . поскольку организация не может выйти из этого состояния. Основная проблема заключается в том, что если существует вероятность банкротства, анализ затрат и выгод становится невозможным». [3] — будет неэргодичным. Все традиционные модели, основанные на стандартной вероятностной статистике, не работают в таких экстремальных ситуациях.
Эргодическая гипотеза в социальных науках
[ редактировать ]В социальных науках эргодическая гипотеза соответствует предположению, что индивиды являются представителями групп, и наоборот, что средние значения группы могут адекватно характеризовать то, что можно увидеть в индивидууме. Похоже, что это не так: данные на уровне группы часто плохо отражают индивидуальные вариации уровня. [4] [5] поскольку индивидуальные стандартные отклонения (SD), как правило, почти в восемь раз превышают стандартные отклонения группового уровня тех же людей. [5] Впоследствии треть отдельных наблюдений выходит за пределы 99,9% доверительного интервала данных группового уровня.
См. также
[ редактировать ]- Эргодический процесс
- Эргодическая теория — раздел математики, занимающийся более общей формулировкой эргодичности.
- Эргодичность
- Парадокс Лошмидта
- Теорема Пуанкаре о возврате
- Эффект Линди
Ссылки
[ редактировать ]- ↑ Первоначально принадлежит Л. Больцману. См. часть 2 Vorlesungen über Gastheorie . Лейпциг: Дж. А. Барт. 1898. OCLC 01712811 . («Эргоден» на стр. 89 в переиздании 1923 года.) Он использовался для доказательства равнораспределения энергии в кинетической теории газов.
- ^ Введение практического аспекта нарушения эргодичности путем введения «шкалы времени неэргодичности» связано с Палмер, Р.Г. (1982). «Нарушенная эргодичность». Достижения физики . 31 (6): 669. Бибкод : 1982AdPhy..31..669P . дои : 10.1080/00018738200101438 . . С этими временными явлениями также связаны свойства старения и теория связи мод. Гетце, В. (2008). Динамика стеклообразующих жидкостей . Оксфордский университет. Нажимать.
- ^ Талеб, Нассим Николас (2019), «Вероятность, риск и крайности» , в Нидхэме, Дункан (редактор), Extremes , Cambridge University Press, стр. 46–66.
- ^ Моленаар, ПК (2004). «Манифест о психологии как идиографической науке: Возвращение человека в научную психологию, на этот раз навсегда» . Измерение . 2 (4): 201–218. дои : 10.1207/s15366359mea0204_1 . S2CID 145323330 .
- ^ Jump up to: а б Фишер, Эй Джей (2018). «Отсутствие возможности обобщения между группами и отдельными людьми представляет собой угрозу для исследований на людях» . ПНАС . 115 (27): 6106–6115. Бибкод : 2018PNAS..115E6106F . дои : 10.1073/pnas.1711978115 . ПМК 6142277 . ПМИД 29915059 .