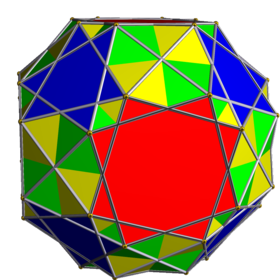
Соединение двух курносых кубиков

Соединение двух курносых кубиков
Тип	Однородный состав
Индекс	УК 68
Символ Шлефли	βр{4,3}
Диаграмма Кокстера
Многогранники	2 курносых кубика
Лица	16+48 треугольников 12 квадратов
Края	120
Вершины	48
Группа симметрии	октаэдрический ( о ч )
Подгруппа, ограничивающаяся одним компонентом	хиральный октаэдр ( O )

Это однородное многогранное соединение представляет собой композицию двух энантиомеров курносого куба . Как голоснуб он представлен символом Шлефли βr{4,3} и диаграммой Кокстера. .

Расположение вершин этого соединения разделяет выпуклый неоднородный усеченный кубооктаэдр с прямоугольными гранями, а также неправильные шестиугольники и восьмиугольники , каждый из которых чередуется с двумя длинами ребер.

Вместе со своей выпуклой оболочкой она представляет собой курносую проекцию неоднородной курносой кубической антипризмы .

Декартовы координаты

Декартовы координаты вершин — все перестановки это

(±1, ± ξ , ±1/ ξ )

где ξ — действительное решение задачи

$\xi ^{3}+\xi ^{2}+\xi =1,\,$

который можно написать

$\xi ={\frac {1}{3}}\left({\sqrt[{3}]{17+3{\sqrt {33}}}}-{\sqrt[{3}]{-17+3{\sqrt {33}}}}-1\right)$

или приблизительно 0,543689. ξ — обратная константа Трибоначчи .

Точно так же константа Трибоначчи t , как и курносый куб , может вычислять координаты как:

(±1, ± t , ± ⁠ 1 / t ⁠ )

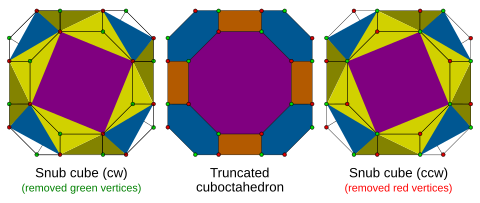
Усеченный кубооктаэдр

Это соединение можно рассматривать как объединение двух киральных чередований усеченного кубооктаэдра :

Геометрическое построение постоянной Трибоначчи (AC) с циркулем и отмеченной линейкой в ​​соответствии с методом, описанным Ксерардо Нейрой.

См. также

• Соединение двух икосаэдров
• Курносый (геометрия)

Ссылки

• Скиллинг, Джон (1976), «Однородные соединения однородных многогранников», Mathematical Proceedings of the Cambridge Philosophical Society , 79 : 447–457, doi : 10.1017/S0305004100052440 , MR   0397554 .