Модуль сдвига

Модуль сдвига
Модуль сдвига
Общие символы	Г , С , мкм
И объединились	Хорошо
Выводы из ; другие количества	G = τ / γ = E /[2(1 + ν )]

В материаловедении модуль модуль сдвига или жесткости , обозначаемый G , а иногда S или μ , является мерой упругой жесткости материала при сдвиге и определяется как отношение напряжения сдвига к деформации сдвига : ^[1]

G\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\tau _{xy}}{\gamma _{xy}}}={\frac {F/A}{\Delta x/l}}={\frac {Fl}{A\Delta x}}

где

\tau _{xy}=F/A\,

= напряжение сдвига

F

это сила, которая действует

A

это площадь, на которую действует сила

\gamma _{xy}

= деформация сдвига. В инженерном деле

:=\Delta x/l=\tan \theta

, в другом месте

:=\theta

\Delta x

поперечное смещение

l

— начальная длина области.

Производной системе СИ единицей модуля сдвига в является паскаль (Па), хотя обычно он выражается в гигапаскалях (ГПа) или тысячах фунтов на квадратный дюйм (ksi). Его размерная форма - M ¹л ⁻¹Т ⁻², заменяя силу на массу , умноженную на ускорение .

Объяснение

Материал	Типичные значения для модуль сдвига (ГПа) (при комнатной температуре)
Алмаз ^[2]	478.0
Сталь ^[3]	79.3
Железо ^[4]	52.5
Медь ^[5]	44.7
Титан ^[3]	41.4
Стекло ^[3]	26.2
Алюминий ^[3]	25.5
полиэтилен ^[3]	0.117
Резина ^[6]	0.0006
Гранит ^[7]^[8]	24
Сланец ^[7]^[8]	1.6
Известняк ^[7]^[8]	24
Мел ^[7]^[8]	3.2
Песчаник ^[7]^[8]	0.4
Древесина	4

Модуль сдвига является одной из нескольких величин для измерения жесткости материалов. Все они возникают в обобщенном законе Гука :

Модуль Юнга E описывает деформационную реакцию материала на одноосное напряжение в направлении этого напряжения (например, натягивание концов проволоки или помещение груза на вершину колонны, при этом проволока становится длиннее, а колонна теряет высоту).
ν коэффициент Пуассона описывает реакцию в направлениях, ортогональных этому одноосному напряжению (проволока становится тоньше, а столбик толще),
модуль объемного сжатия K описывает реакцию материала на (равномерное) гидростатическое давление (например, давление на дне океана или в глубоком бассейне),
модуль сдвига G описывает реакцию материала на напряжение сдвига (например, разрезание его тупыми ножницами).

Эти модули не являются независимыми и для изотропных материалов связаны уравнениями ^[9]

E=2G(1+\nu )=3K(1-2\nu )

Модуль сдвига связан с деформацией твердого тела, когда на него действует сила, параллельная одной из его поверхностей, в то время как на его противоположную сторону действует противодействующая сила (например, трение). В случае объекта, имеющего форму прямоугольной призмы, он деформируется в параллелепипед . Анизотропные материалы, такие как дерево , бумага , а также практически все монокристаллы, демонстрируют различную реакцию материала на напряжение или деформацию при испытании в разных направлениях. В этом случае может потребоваться использовать полное тензорное выражение упругих констант, а не одно скалярное значение.

Одним из возможных определений жидкости может быть материал с нулевым модулем сдвига.

Поперечные волны

В однородных и изотропных твердых телах существуют два типа волн: волны давления и поперечные волны . Скорость поперечной волны, $(v_{s})$ контролируется модулем сдвига,

v_{s}={\sqrt {\frac {G}{\rho }}}

где

G — модуль сдвига

\rho

твердого тела – плотность .

Модуль сдвига металлов

Модуль сдвига меди как функция температуры. Экспериментальные данные ^[11]^[12] показаны цветными символами.

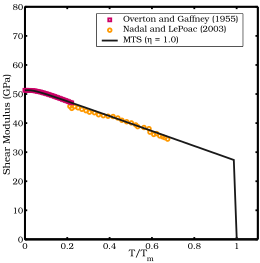
Обычно наблюдается уменьшение модуля сдвига металлов с повышением температуры. При высоких давлениях модуль сдвига также увеличивается с увеличением приложенного давления. Корреляции между температурой плавления, энергией образования вакансий и модулем сдвига наблюдались во многих металлах. ^[13]

Существует несколько моделей, которые пытаются предсказать модуль сдвига металлов (и, возможно, сплавов). Модели модуля сдвига, которые использовались в расчетах пластического течения, включают:

модель Варшни-Чен-Грея, разработанная ^[14] и используется в сочетании с моделью напряжения пластического течения «Механическое пороговое напряжение» (MTS). ^[15]^[16]
модель модуля сдвига Стейнберга-Кокрана-Гинана (SCG), разработанная ^[17] и используется в сочетании с моделью напряжения течения Стейнберга-Кокрана-Гинана-Лунда (SCGL).
модель модуля сдвига Надаля и ЛеПоака (NP) ^[12] который использует теорию Линдеманна для определения температурной зависимости и модель SCG для зависимости модуля сдвига от давления.

Модель Варшни-Чен-Грея

Модель Варшни-Чена-Грея (иногда называемая уравнением Варшни) имеет вид:

\mu (T)=\mu _{0}-{\frac {D}{\exp(T_{0}/T)-1}}

где $\mu _{0}$ модуль сдвига при $T=0K$ , и $D$ и $T_{0}$ являются материальными константами.

Модель СКГ

Модель модуля сдвига Стейнберга-Кокрана-Гинана (SCG) зависит от давления и имеет вид

\mu (p,T)=\mu _{0}+{\frac {\partial \mu }{\partial p}}{\frac {p}{\eta ^{\frac {1}{3}}}}+{\frac {\partial \mu }{\partial T}}(T-300);\quad \eta :={\frac {\rho }{\rho _{0}}}

где µ ₀ — модуль сдвига в исходном состоянии ( T = 300 К, p = 0, η = 1), p — давление, T — температура.

НП-модель

Модель модуля сдвига Надаля-Ле Поака (NP) представляет собой модифицированную версию модели SCG. Эмпирическая температурная зависимость модуля сдвига в модели SCG заменена уравнением, основанным на теории плавления Линдемана . Модель модуля сдвига NP имеет вид:

\mu (p,T)={\frac {1}{{\mathcal {J}}\left({\hat {T}}\right)}}\left[\left(\mu _{0}+{\frac {\partial \mu }{\partial p}}{\frac {p}{\eta ^{\frac {1}{3}}}}\right)\left(1-{\hat {T}}\right)+{\frac {\rho }{Cm}}~T\right];\quad C:={\frac {\left(6\pi ^{2}\right)^{\frac {2}{3}}}{3}}f^{2}

где

{\mathcal {J}}({\hat {T}}):=1+\exp \left[-{\frac {1+1/\zeta }{1+\zeta /\left(1-{\hat {T}}\right)}}\right]\quad {\text{for}}\quad {\hat {T}}:={\frac {T}{T_{m}}}\in [0,6+\zeta ],

µ ₀ — модуль сдвига при абсолютном нуле и окружающем давлении, ζ — площадь, m — атомная масса , а f — постоянная Линдемана .

Модуль сдвиговой релаксации

Модуль сдвиговой релаксации $G(t)$ - зависящее от времени обобщение модуля сдвига ^[18] $G$ :

G=\lim _{t\to \infty }G(t)

.

См. также

Ссылки

^ ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Модуль сдвига, G ». дои : 10.1351/goldbook.S05635
^ Макскимин, HJ; Андреатч, П. (1972). «Модули упругости алмаза как функция давления и температуры». Дж. Прил. Физ . 43 (7): 2944–2948. Бибкод : 1972JAP....43.2944M . дои : 10.1063/1.1661636 .
^ Jump up to: ^а ^б ^с ^д ^и Крэндалл, Даль, Ларднер (1959). Введение в механику твердого тела . Бостон: МакГроу-Хилл. ISBN 0-07-013441-3 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Рейн, Дж. А. (1961). «Упругие константы железа от 4,2 до 300°К». Физический обзор . 122 (6): 1714–1716. Бибкод : 1961PhRv..122.1714R . дои : 10.1103/PhysRev.122.1714 .
^ Свойства материала
^ Спанос, Пит (2003). «Влияние системы отверждения на низкотемпературный динамический модуль сдвига натурального каучука» . Резиновый мир .
^ Jump up to: ^а ^б ^с ^д ^и Хук, Эверт и Джонатан Д. Брей. Проектирование скальных склонов. ЦРК Пресс, 1981.
^ Jump up to: ^а ^б ^с ^д ^и Паризо, Уильям Г. Анализ конструкции в механике горных пород. ЦРК Пресс, 2017.
^ [Ландау Л.Д., Лифшиц Э.М. Теория упругости , вып. 7. Курс теоретической физики. (2-е изд.) Пергамон: Оксфорд, 1970, стр. 13]
^ Расчет модуля сдвига стекол.
^ Овертон, В.; Гаффни, Джон (1955). «Температурное изменение упругих констант кубических элементов. I. Медь». Физический обзор . 98 (4): 969. Бибкод : 1955PhRv...98..969O . дои : 10.1103/PhysRev.98.969 .
^ Jump up to: ^а ^б Надаль, Мари-Элен; Ле Поак, Филипп (2003). «Непрерывная модель модуля сдвига как функция давления и температуры до точки плавления: анализ и ультразвуковая проверка». Журнал прикладной физики . 93 (5): 2472. Бибкод : 2003JAP....93.2472N . дои : 10.1063/1.1539913 .
^ Марч, Нью-Хэмпшир, (1996), Электронная корреляция в молекулах и конденсированных фазах , Springer, ISBN 0-306-44844-0 стр. 363
^ Варшни, Ю. (1970). «Температурная зависимость упругих констант». Физический обзор B . 2 (10): 3952–3958. Бибкод : 1970PhRvB...2.3952V . дои : 10.1103/PhysRevB.2.3952 .
^ Чен, Шу Ронг; Грей, Джордж Т. (1996). «Основное поведение тантала и тантал-вольфрамовых сплавов» . Металлургические и сырьевые операции А . 27 (10): 2994. Бибкод : 1996MMTA...27.2994C . дои : 10.1007/BF02663849 . S2CID 136695336 .
^ Гото, ДМ; Гарретт, РК; Бингерт, Дж. Ф.; Чен, СР; Грей, GT (2000). «Описание модели конститутивной прочности механического порогового напряжения стали HY-100» (PDF) . Металлургические и сырьевые операции А . 31 (8): 1985–1996. Бибкод : 2000ММТА...31.1985Г . дои : 10.1007/s11661-000-0226-8 . S2CID 136118687 . Архивировано из оригинала 25 сентября 2017 года.
^ Гинан, М; Стейнберг, Д. (1974). «Производные изотропного поликристаллического модуля сдвига по давлению и температуре для 65 элементов». Журнал физики и химии твердого тела . 35 (11): 1501. Бибкод : 1974JPCS...35.1501G . дои : 10.1016/S0022-3697(74)80278-7 .
^ Рубинштейн, Михаил, 20 декабря 1956 г. (2003 г.). Физика полимеров . Колби, Ральф Х. Оксфорд: Издательство Оксфордского университета. п. 284. ИСБН 019852059X . OCLC 50339757 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )

Формулы преобразования
Однородные изотропные линейно-упругие материалы имеют упругие свойства, однозначно определяемые любыми двумя модулями из них; таким образом, учитывая любые два, любой другой из модулей упругости можно рассчитать по этим формулам, приведенным как для 3D-материалов (первая часть таблицы), так и для 2D-материалов (вторая часть).
3D-формулы	$K=\,$	$E=\,$	$\lambda =\,$	$G=\,$	$\nu =\,$	$M=\,$	Примечания
$(K,\,E)$			${\tfrac {3K(3K-E)}{9K-E}}$	${\tfrac {3KE}{9K-E}}$	${\tfrac {3K-E}{6K}}$	${\tfrac {3K(3K+E)}{9K-E}}$
$(K,\,\lambda )$		${\tfrac {9K(K-\lambda )}{3K-\lambda }}$		${\tfrac {3(K-\lambda )}{2}}$	${\tfrac {\lambda }{3K-\lambda }}$	$3K-2\lambda \,$
$(K,\,G)$		${\tfrac {9KG}{3K+G}}$	$K-{\tfrac {2G}{3}}$		${\tfrac {3K-2G}{2(3K+G)}}$	$K+{\tfrac {4G}{3}}$
$(K,\,\nu )$		$3K(1-2\nu )\,$	${\tfrac {3K\nu }{1+\nu }}$	${\tfrac {3K(1-2\nu )}{2(1+\nu )}}$		${\tfrac {3K(1-\nu )}{1+\nu }}$
$(K,\,M)$		${\tfrac {9K(M-K)}{3K+M}}$	${\tfrac {3K-M}{2}}$	${\tfrac {3(M-K)}{4}}$	${\tfrac {3K-M}{3K+M}}$
$(E,\,\lambda )$	${\tfrac {E+3\lambda +R}{6}}$			${\tfrac {E-3\lambda +R}{4}}$	${\tfrac {2\lambda }{E+\lambda +R}}$	${\tfrac {E-\lambda +R}{2}}$	$R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}$
$(E,\,G)$	${\tfrac {EG}{3(3G-E)}}$		${\tfrac {G(E-2G)}{3G-E}}$		${\tfrac {E}{2G}}-1$	${\tfrac {G(4G-E)}{3G-E}}$
$(E,\,\nu )$	${\tfrac {E}{3(1-2\nu )}}$		${\tfrac {E\nu }{(1+\nu )(1-2\nu )}}$	${\tfrac {E}{2(1+\nu )}}$		${\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}$
$(E,\,M)$	${\tfrac {3M-E+S}{6}}$		${\tfrac {M-E+S}{4}}$	${\tfrac {3M+E-S}{8}}$	${\tfrac {E-M+S}{4M}}$		$S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}$ Есть два верных решения. Знак плюс приводит к $\nu \geq 0$ . Знак минус приводит к $\nu \leq 0$ .
$(\lambda ,\,G)$	$\lambda +{\tfrac {2G}{3}}$	${\tfrac {G(3\lambda +2G)}{\lambda +G}}$			${\tfrac {\lambda }{2(\lambda +G)}}$	$\lambda +2G\,$
$(\lambda ,\,\nu )$	${\tfrac {\lambda (1+\nu )}{3\nu }}$	${\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}$		${\tfrac {\lambda (1-2\nu )}{2\nu }}$		${\tfrac {\lambda (1-\nu )}{\nu }}$	Нельзя использовать, когда $\nu =0\Leftrightarrow \lambda =0$
$(\lambda ,\,M)$	${\tfrac {M+2\lambda }{3}}$	${\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}$		${\tfrac {M-\lambda }{2}}$	${\tfrac {\lambda }{M+\lambda }}$
$(G,\,\nu )$	${\tfrac {2G(1+\nu )}{3(1-2\nu )}}$	$2G(1+\nu )\,$	${\tfrac {2G\nu }{1-2\nu }}$			${\tfrac {2G(1-\nu )}{1-2\nu }}$
$(G,\,M)$	$M-{\tfrac {4G}{3}}$	${\tfrac {G(3M-4G)}{M-G}}$	$M-2G\,$		${\tfrac {M-2G}{2M-2G}}$
$(\nu ,\,M)$	${\tfrac {M(1+\nu )}{3(1-\nu )}}$	${\tfrac {M(1+\nu )(1-2\nu )}{1-\nu }}$	${\tfrac {M\nu }{1-\nu }}$	${\tfrac {M(1-2\nu )}{2(1-\nu )}}$
2D-формулы	$K_{\mathrm {2D} }=\,$	$E_{\mathrm {2D} }=\,$	$\lambda _{\mathrm {2D} }=\,$	$G_{\mathrm {2D} }=\,$	$\nu _{\mathrm {2D} }=\,$	$M_{\mathrm {2D} }=\,$	Примечания
$(K_{\mathrm {2D} },\,E_{\mathrm {2D} })$			${\tfrac {2K_{\mathrm {2D} }(2K_{\mathrm {2D} }-E_{\mathrm {2D} })}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}$	${\tfrac {K_{\mathrm {2D} }E_{\mathrm {2D} }}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}$	${\tfrac {2K_{\mathrm {2D} }-E_{\mathrm {2D} }}{2K_{\mathrm {2D} }}}$	${\tfrac {4K_{\mathrm {2D} }^{2}}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}$
$(K_{\mathrm {2D} },\,\lambda _{\mathrm {2D} })$		${\tfrac {4K_{\mathrm {2D} }(K_{\mathrm {2D} }-\lambda _{\mathrm {2D} })}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}$		$K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }$	${\tfrac {\lambda _{\mathrm {2D} }}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}$	$2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }$
$(K_{\mathrm {2D} },\,G_{\mathrm {2D} })$		${\tfrac {4K_{\mathrm {2D} }G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}$	$K_{\mathrm {2D} }-G_{\mathrm {2D} }$		${\tfrac {K_{\mathrm {2D} }-G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}$	$K_{\mathrm {2D} }+G_{\mathrm {2D} }$
$(K_{\mathrm {2D} },\,\nu _{\mathrm {2D} })$		$2K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })\,$	${\tfrac {2K_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}$	${\tfrac {K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{1+\nu _{\mathrm {2D} }}}$		${\tfrac {2K_{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}$
$(E_{\mathrm {2D} },\,G_{\mathrm {2D} })$	${\tfrac {E_{\mathrm {2D} }G_{\mathrm {2D} }}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}$		${\tfrac {2G_{\mathrm {2D} }(E_{\mathrm {2D} }-2G_{\mathrm {2D} })}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}$		${\tfrac {E_{\mathrm {2D} }}{2G_{\mathrm {2D} }}}-1$	${\tfrac {4G_{\mathrm {2D} }^{2}}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}$
$(E_{\mathrm {2D} },\,\nu _{\mathrm {2D} })$	${\tfrac {E_{\mathrm {2D} }}{2(1-\nu _{\mathrm {2D} })}}$		${\tfrac {E_{\mathrm {2D} }\nu _{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}$	${\tfrac {E_{\mathrm {2D} }}{2(1+\nu _{\mathrm {2D} })}}$		${\tfrac {E_{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}$
$(\lambda _{\mathrm {2D} },\,G_{\mathrm {2D} })$	$\lambda _{\mathrm {2D} }+G_{\mathrm {2D} }$	${\tfrac {4G_{\mathrm {2D} }(\lambda _{\mathrm {2D} }+G_{\mathrm {2D} })}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}$			${\tfrac {\lambda _{\mathrm {2D} }}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}$	$\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }\,$
$(\lambda _{\mathrm {2D} },\,\nu _{\mathrm {2D} })$	${\tfrac {\lambda _{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}$	${\tfrac {\lambda _{\mathrm {2D} }(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}{\nu _{\mathrm {2D} }}}$		${\tfrac {\lambda _{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}$		${\tfrac {\lambda _{\mathrm {2D} }}{\nu _{\mathrm {2D} }}}$	Нельзя использовать, когда $\nu _{\mathrm {2D} }=0\Leftrightarrow \lambda _{\mathrm {2D} }=0$
$(G_{\mathrm {2D} },\,\nu _{\mathrm {2D} })$	${\tfrac {G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{1-\nu _{\mathrm {2D} }}}$	$2G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })\,$	${\tfrac {2G_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}$			${\tfrac {2G_{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}$
$(G_{\mathrm {2D} },\,M_{\mathrm {2D} })$	$M_{\mathrm {2D} }-G_{\mathrm {2D} }$	${\tfrac {4G_{\mathrm {2D} }(M_{\mathrm {2D} }-G_{\mathrm {2D} })}{M_{\mathrm {2D} }}}$	$M_{\mathrm {2D} }-2G_{\mathrm {2D} }\,$		${\tfrac {M_{\mathrm {2D} }-2G_{\mathrm {2D} }}{M_{\mathrm {2D} }}}$

[1] ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Модуль сдвига, G ». дои : 10.1351/goldbook.S05635

[McSkimin-2] Макскимин, HJ; Андреатч, П. (1972). «Модули упругости алмаза как функция давления и температуры». Дж. Прил. Физ . 43 (7): 2944–2948. Бибкод : 1972JAP....43.2944M . дои : 10.1063/1.1661636 .

[CDL-3] Jump up to: ^а ^б ^с ^д ^и Крэндалл, Даль, Ларднер (1959). Введение в механику твердого тела . Бостон: МакГроу-Хилл. ISBN 0-07-013441-3 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[rayne61-4] Рейн, Дж. А. (1961). «Упругие константы железа от 4,2 до 300°К». Физический обзор . 122 (6): 1714–1716. Бибкод : 1961PhRv..122.1714R . дои : 10.1103/PhysRev.122.1714 .

[5] Свойства материала

[Spanos-6] Спанос, Пит (2003). «Влияние системы отверждения на низкотемпературный динамический модуль сдвига натурального каучука» . Резиновый мир .

[Hoek-7] Jump up to: ^а ^б ^с ^д ^и Хук, Эверт и Джонатан Д. Брей. Проектирование скальных склонов. ЦРК Пресс, 1981.

[Pariseau-8] Jump up to: ^а ^б ^с ^д ^и Паризо, Уильям Г. Анализ конструкции в механике горных пород. ЦРК Пресс, 2017.

[9] [Ландау Л.Д., Лифшиц Э.М. Теория упругости , вып. 7. Курс теоретической физики. (2-е изд.) Пергамон: Оксфорд, 1970, стр. 13]

[10] Расчет модуля сдвига стекол.

[Overton55-11] Овертон, В.; Гаффни, Джон (1955). «Температурное изменение упругих констант кубических элементов. I. Медь». Физический обзор . 98 (4): 969. Бибкод : 1955PhRv...98..969O . дои : 10.1103/PhysRev.98.969 .

[Nadal03-12] Jump up to: ^а ^б Надаль, Мари-Элен; Ле Поак, Филипп (2003). «Непрерывная модель модуля сдвига как функция давления и температуры до точки плавления: анализ и ультразвуковая проверка». Журнал прикладной физики . 93 (5): 2472. Бибкод : 2003JAP....93.2472N . дои : 10.1063/1.1539913 .

[March-13] Марч, Нью-Хэмпшир, (1996), Электронная корреляция в молекулах и конденсированных фазах , Springer, ISBN 0-306-44844-0 стр. 363

[Varshni70-14] Варшни, Ю. (1970). «Температурная зависимость упругих констант». Физический обзор B . 2 (10): 3952–3958. Бибкод : 1970PhRvB...2.3952V . дои : 10.1103/PhysRevB.2.3952 .

[Chen96-15] Чен, Шу Ронг; Грей, Джордж Т. (1996). «Основное поведение тантала и тантал-вольфрамовых сплавов» . Металлургические и сырьевые операции А . 27 (10): 2994. Бибкод : 1996MMTA...27.2994C . дои : 10.1007/BF02663849 . S2CID 136695336 .

[Goto00-16] Гото, ДМ; Гарретт, РК; Бингерт, Дж. Ф.; Чен, СР; Грей, GT (2000). «Описание модели конститутивной прочности механического порогового напряжения стали HY-100» (PDF) . Металлургические и сырьевые операции А . 31 (8): 1985–1996. Бибкод : 2000ММТА...31.1985Г . дои : 10.1007/s11661-000-0226-8 . S2CID 136118687 . Архивировано из оригинала 25 сентября 2017 года.

[Guinan74-17] Гинан, М; Стейнберг, Д. (1974). «Производные изотропного поликристаллического модуля сдвига по давлению и температуре для 65 элементов». Журнал физики и химии твердого тела . 35 (11): 1501. Бибкод : 1974JPCS...35.1501G . дои : 10.1016/S0022-3697(74)80278-7 .

[18] Рубинштейн, Михаил, 20 декабря 1956 г. (2003 г.). Физика полимеров . Колби, Ральф Х. Оксфорд: Издательство Оксфордского университета. п. 284. ИСБН 019852059X . OCLC 50339757 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка )

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]