Номограмма

Номограмма ( (от греческой νόμος (nomos) 'Law' и γραμμή Grammē) 'Line'), также называемая номографией , диаграммой выравнивания или ABAC , представляет собой графическое расчетное устройство , двумерная диаграмма, разработанная для обеспечения приблизительного графического устройства. Вычисление математической функции . Поле нодографии была изобретена в 1884 году французским инженером Филбертом Морисом Д'Кэгном (1862–1938) и широко использовался в течение многих лет, чтобы предоставить инженерам быстрые графические расчеты сложных формул для практической точности. Номограммы используют параллельную систему координат , изобретенную D'Ocagne, а не стандартные декартовые координаты .

Номограмма состоит из набора n шкал, по одной для каждой переменной в уравнении. Зная значения переменных N-1, можно найти значение неизвестной переменной или зафиксируя значения некоторых переменных, можно изучить взаимосвязь между нефиксированными. Результат получается путем укладки прямоугольника по известным значениям на шкалах и считывающим неизвестное значение, откуда он пересекает шкалу для этой переменной. Виртуальная или нарисованная линия, созданная линейкой, называется индексной линией или изоптом .

Номограммы процветали во многих различных контекстах в течение примерно 75 лет, потому что они допускали быстрые и точные вычисления до возраста карманных калькуляторов. Результаты от номограммы получаются очень быстро и надежно, просто рисуя одну или несколько линий. Пользователь не должен знать, как решать алгебраические уравнения, просматривать данные в таблицах, использовать правило слайда или заменить числа в уравнения для получения результатов. Пользователю даже не нужно знать основное уравнение, которое представляет номограмма. Кроме того, номограммы естественным образом включают неявные или явные знания области в свой дизайн. Например, для создания более крупных номограмм для большей точности номограф обычно включает в себя только диапазоны масштаба, которые являются разумными и представляют интерес для этой проблемы. Многие номограммы включают в себя другие полезные маркировки, такие как эталонные этикетки и цветные регионы. Все это предоставляет полезные руководящие точки пользователю.

Как правило слайда, номограмма является графическим аналоговым устройством вычисления. Также как правило слайдов, его точность ограничена точностью, с которой физические маркировки могут быть нарисованы, воспроизведены, просмотрены и выровнены. В отличие от правила слайда, которое является общепринятым вычислительным устройством, номограмма предназначена для выполнения конкретного расчета с таблицами значений, встроенных в шкалы устройства . Номограммы обычно используются в приложениях, для которых уровень точности, который они обеспечивают, является достаточным и полезным. Альтернативно, номограмма может использоваться для проверки ответа, полученного более точным, но подверженным ошибкам расчета.

Другие типы графических калькуляторов, такие как графики перехвата , трилинейные диаграммы и шестиугольные диаграммы , иногда называются номограммами. Эти устройства не соответствуют определению номограммы как графического калькулятора, решение которого обнаружено с помощью одной или нескольких линейных изоптов.

Описание

Номограмма для уравнения с тремя переменными, как правило, имеет три шкалы, хотя существуют номограммы, в которых распространены две или даже все три шкалы. Здесь две шкалы представляют известные значения, а третье - шкала, где результат считывается. Самое простое такое уравнение - U ₁ + U ₂ + U ₃ = 0 для трех переменных U ₁ , U ₂ и U ₃ . Пример этого типа номограммы показан справа, аннотируется терминами, используемыми для описания частей номограммы.

Более сложные уравнения иногда могут быть выражены как сумма функций трех переменных. Например, номограмма в верхней части этой статьи может быть построена как номограмма параллельной масштаба, потому что она может быть выражена как такая сумма после принятия логарифмов обеих сторон уравнения.

Шкала для неизвестной переменной может лежать между двумя другими шкалами или за пределами их. Известные значения расчета отмечены в масштабах для этих переменных, и между этими оценками проводятся линия. Результат считывается из неизвестной шкалы в точке, где линия пересекает этот масштаб. Шкалы включают в себя «метки», чтобы указать точные местоположения чисел, и они также могут включать помеченные эталонные значения. Эти масштабы могут быть линейными , логарифмическими или иметь более сложные отношения.

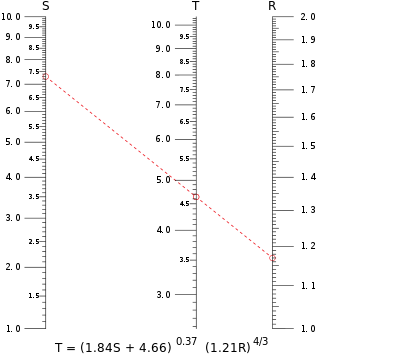
Образец изоплат, показанный красным, на номограмме в верхней части этой статьи вычисляет значение t , когда s = 7,30 и r = 1,17. Изоплат пересекает шкалу для Т чуть менее 4,65; Большая фигура, напечатанная в высоком разрешении на бумаге, даст t = 4,64 до трехзначного точность. Обратите внимание, что любая переменная может быть рассчитана по значениям двух других, функции номограмм, которая особенно полезна для уравнений, в которых переменная не может быть алгебраически выделена из других переменных.

Прямые масштабы полезны для относительно простых расчетов, но для более сложных расчетов может потребоваться использование простых или сложных изогнутых шкал. Номограммы для более чем трех переменных могут быть построены путем включения сетки масштабов для двух из переменных или путем объединения отдельных номограммов меньшего количества переменных в составную номограмму.

Приложения

Номограммы использовались в широком спектре приложений. Образец включает в себя:

Первоначальное применение D'Ocagne, автоматизация сложных расчетов с разрезанием и заполнением для удаления земли во время строительства французской национальной железнодорожной системы. Это было важным доказательством концепции, потому что расчеты являются нетривиальными, а результаты переведены в значительную экономию времени, усилий и денег.
Конструкция каналов, труб и проводов для регулирования потока воды.
Работа Лоуренса Хендерсона , в которой номограммы использовались для корреляции многих различных аспектов физиологии крови. Это было первое крупное использование номограмм в Соединенных Штатах, а также первые медицинские номограммы в любом месте. ^{[ Цитация необходима ]}
Медицинские области, такие как аптека и онкология. ^{[ 1 ]}
Баллистические расчеты перед системами управления огнем, где время расчета было критическим.
Расчеты механического цеха, для преобразования размеров Blueprint и выполнения расчетов на основе размеров и свойств материала. Эти номограммы часто включали маркировку для стандартных размеров и для доступных промышленных деталей.
Статистика для сложных расчетов свойств распределений и для исследований операций, включая проектирование тестов приемлемости для контроля качества.
Операционные исследования, чтобы получить результаты в различных проблемах оптимизации.
Химия и химическая инженерия, чтобы инкапсулировать как общие физические отношения, так и эмпирические данные для конкретных соединений.
Аэронавтика, в которой номограммы использовались десятилетиями в кабинах самолетов всех описаний. В качестве навигационной помощи и управления полетом номограммы были быстрыми, компактными и простыми в использовании калькуляторов.
после запуска Астрономические расчеты, как в орбитальных расчетах Спутника 1 . ^{[ 2 ]}
Инженерная работа всех видов: электрическая конструкция фильтров и линий передачи, механические расчеты напряжений и нагрузки, оптические расчеты и т. Д.
Военные, где должны быть сделаны сложные расчеты быстро и с надежностью, не зависящей от электрических устройств.
Сейсмология , где были разработаны номограммы для оценки величины землетрясения и для представления результатов вероятностного сейсмической опасности анализа ^{[ 3 ]}

Примеры

Параллельная устойчивость/тонкая линза

Параллельная электрическая стойкость номограмма

Приведенная ниже номограмма выполняет вычисление:

$f(A,B)={\frac {1}{1/A+1/B}}={\frac {AB}{A+B}}$

Эта номограмма интересна, потому что она выполняет полезный нелинейный расчет, используя только прямые, одинаково градуированные масштабы. В то время как диагональная линия имеет масштаб ${\sqrt {2}}$ Время превышает масштабы оси, числа на нем точно соответствуют цифрам непосредственно внизу или слева, и, следовательно, их можно легко создать, нарисовав прямую линию по диагонали на листе графической бумаги .

A и B вводятся на горизонтальные и вертикальные масштабы, и результат считывается из диагональной шкалы. Будучи пропорциональными гармоническому среднему значению A и B , эта формула имеет несколько приложений. Например, это формула параллельной устойчивости в электронике и уравнение тонкой линзы в оптике .

В примере красная линия демонстрирует, что параллельные резисторы 56 и 42 Ом имеют комбинированное сопротивление 24 Ом. Это также демонстрирует, что объект на расстоянии 56 см от объектива , фокусное расстояние , 24 см составляет реальное изображение на расстоянии 42 см.

Вычисление теста хи-квадрат

Приведенная ниже номограмма может быть использована для приблизительного вычисления некоторых значений, необходимых при выполнении знакомого статистического теста, теста на хи-квадрат Пирсона . Эта номограмма демонстрирует использование изогнутых масштабов с неравномерно распределенными градами.

Соответствующее выражение:

${\frac {(OBS-EXP)^{2}}{EXP}}$

Шкала вдоль вершины разделяется между пятью различными диапазонами наблюдаемых значений: A, B, C, D и E. Наблюдаемое значение обнаруживается в одном из этих диапазонов, и отметка клека Затем изогнутая шкала, используемая для ожидаемого значения, выбрана на основе диапазона. Например, наблюдаемое значение 9 будет использовать отметку клещей выше 9 в диапазоне A, а изогнутая шкала A будет использоваться для ожидаемого значения. Наблюдаемое значение 81 будет использовать отметку клещей выше 81 в диапазоне E, а изогнутая шкала E будет использоваться для ожидаемого значения. Это позволяет включать пять различных номограмм в одну диаграмму.

Таким образом, синяя линия демонстрирует вычисление:

(9 − 5) ² / 5 = 3.2

и красная линия демонстрирует вычисление:

(81 − 70) ² / 70 = 1.7

При выполнении теста коррекция Йейтса к непрерывности часто применяется и просто включает вычитание 0,5 из наблюдаемых значений. Номограмма для выполнения теста с коррекцией Йейтса может быть сконструирована просто путем смещения каждой «наблюдаемой» шкалы половиной единицы влево, так что 1,0, 2,0, 3,0, ... градаты размещаются там, где значения 0,5, 1,5, 2,5 , ... появляется на нынешней таблице.

Оценка пищевого риска

Хотя номограммы представляют математические отношения, не все математически получены. Следующее было разработано графически для достижения соответствующих конечных результатов, которые можно легко определить продуктом их отношений в субъективных единицах, а не численно. Использование непараллельных осей позволило включить нелинейные отношения в модель.

Числа в квадратных коробках обозначают оси, требующие ввода после соответствующей оценки.

Пара номограмм в верхней части изображения определяет вероятность возникновения и доступности, которые затем включаются в нижнюю многоступенчатую номограмму.

Линии 8 и 10 представляют собой «линии связывания» или «линии поворота» и используются для перехода между этапами составной номограммы.

Последняя пара параллельных логарифмических шкал (12) не являются номограммами как таковые, а шкалы считывания для перевода оценки риска (11, отдаленных к чрезвычайно высоким) в частоту выборки для решения аспектов безопасности и других аспектов «защиты потребителей» соответственно Полем Этот этап требует политической «покупки» в балансировке затрат против риска. В примере используется трехлетняя минимальная частота для каждого, хотя с высоким концом риска масштабов, различных для двух аспектов, давая различные частоты для двух, но оба подлежат общей минимальной выборке каждой пищи для всех аспектов, по крайней мере, по крайней мере раз в три года.

Эта номограмма оценки риска была разработана Общественным аналитиком Великобритании с финансированием Агентства по пищевым стандартам Великобритании для использования в качестве инструмента для руководства соответствующей частотой отбора проб и анализа продуктов питания для официальных целей контроля пищевых продуктов, предназначенных для оценки всех потенциалов Проблемы со всеми продуктами, хотя еще не приняты.

Другие быстрые номограммы

Используя линейку, можно легко прочитать недостающий член закона синусов или корни квадратичного и кубического уравнения. ^{[ 4 ]}

Номограмма за закон синусов
Номограмма для решения квадратрического x^2+px+q = 0
Номограмма для решения кубического x^3+px+q = 0

Смотрите также

Ссылки

^ Ха, Юн-Сок; Kim, Tae-Hwan (2018-01-01), Ku, Ja Hyeon (ed.), «Глава 30-Наблюдение за раком мочевого пузыря (MIBC)» , «Рак мочевого пузыря , академическая пресса», стр. 553–597 , doi : 10.1016/b978-0-12-809939-1.00030-8 , ISBN 978-0-12-809939-1 Получено 2022-11-11
^ Yu.a.mozzhorin Memories Archived 2007-10-18 на машине Wayback на веб-сайте Российского государственного архива для научной технологической документации
^ Дуглас, Джон; Danciu, Laurentiu (2019-11-08). «Номограмма, чтобы помочь объяснить вероятностную сейсмическую опасность» . Журнал сейсмологии . 24 (1): 221–228. Bibcode : 2020jseis..24..221d . doi : 10.1007/s10950-019-09885-4 . HDL : 20.500.11850/379252 . ISSN 1573-157X .
^ Szalkai, Istvan; Балинт, Роланд (2017-12-28). «Номограммы для квадратичных и кубических уравнений (у венгерских)» (PDF) . Продвинутая публикация . 2017 .

Дальнейшее чтение

DP Adams, Nomography: теория и применение , (Archon Books) 1964.
HJ Allcock, J. Reginald Jones и JGL Michel, The Nomogram. Теория и практическое строительство расчетных диаграмм , 5 -е изд. (Лондон: сэр Исаак Питман и сыновья, Ltd.) 1963. ( 1 -е издание 1932 )
S. Brodestsky, первый курс по номографии (Лондон, G. Bell and Sons) 1920.
Д.С. Дэвис, Эмпирические уравнения и номография , (Нью-Йорк: McGraw-Hill Book Co.) 1943.
М. Д'Кэгне: Трактат по именам , (Gauthier-Villars, Paris) 1899.
M. D'Ocagne: (1900) о номографическом разрешении уравнения седьмой степени . Отчеты (Париж), 131, 522–524.
Rd Douglass и DP Adams, Elements of Nomography , (Нью-Йорк: McGraw-Hill) 1947.
RP Hoelscher, et al., Графические средства в инженерных вычислениях , (Нью-Йорк: McGraw-Hill) 1952.
Л. Иван Эпштейн, Номография , (Нью -Йорк: Interscience Publishers) 1958.
LH Johnson, Номография и эмпирические уравнения , (Нью -Йорк: Джон Вили и сыновья) 1952.
М. Каттан и Дж. Мараско. (2010) Что такое настоящая номограмма? , Семинары в онкологии, 37 (1), 23–26.
Как Levens, Nomography , 2 -е изд., (Нью -Йорк: John Wiley & Sons, Inc.) 1959.
Ft Mavis, Строительство номографических диаграмм , (Scranton, International Resturbook) 1939.
Э. Отто, Номография , (Нью -Йорк: Компания Macmillan) 1963.
Ha Evesham История и развитие номографии , (Бостон: Docent Press) 2010. ISBN 9781456479626
Th Gronwall, R. Doerfler, A. Gluchoff и S. Guthery, Расчет кривых: математика, история и эстетическая привлекательность номографической работы Th Gronwall , (Бостон: Docent Press) 2012. ISBN 9780983700432

Внешние ссылки

Искусство номографии описывает дизайн номограмм с использованием геометрии, детерминантов и преобразований.
Потерянное искусство номографии - это статья в журнале Math Journal, рассматривая область номографии.
Номограммы для Wargames , но также представляют общий интерес.
Pynomo - программное обеспечение с открытым исходным кодом для построения номограмм.
Java Applet Archived 2009-09-24 на машине Wayback для построения простых номограмм.
Номограммы для визуализации отношений между тремя переменными - видео и слайды приглашенных выступлений Джонатана Ружье для пользователя! 2011.

[1] Ха, Юн-Сок; Kim, Tae-Hwan (2018-01-01), Ku, Ja Hyeon (ed.), «Глава 30-Наблюдение за раком мочевого пузыря (MIBC)» , «Рак мочевого пузыря , академическая пресса», стр. 553–597 , doi : 10.1016/b978-0-12-809939-1.00030-8 , ISBN 978-0-12-809939-1 Получено 2022-11-11

[2] Yu.a.mozzhorin Memories Archived 2007-10-18 на машине Wayback на веб-сайте Российского государственного архива для научной технологической документации

[3] Дуглас, Джон; Danciu, Laurentiu (2019-11-08). «Номограмма, чтобы помочь объяснить вероятностную сейсмическую опасность» . Журнал сейсмологии . 24 (1): 221–228. Bibcode : 2020jseis..24..221d . doi : 10.1007/s10950-019-09885-4 . HDL : 20.500.11850/379252 . ISSN 1573-157X .

[4] Szalkai, Istvan; Балинт, Роланд (2017-12-28). «Номограммы для квадратичных и кубических уравнений (у венгерских)» (PDF) . Продвинутая публикация . 2017 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]