диаграмма Смита

Чтобы узнать о других значениях термина «диаграмма Смита», см. Диаграмма Смита (значения) .

«Диаграмма Вольперта» перенаправляется сюда. Для аналогичного термина «график Вольперта» см. « график Вольперта» (значения) .

Диаграмма Смита (иногда также называемая диаграммой Смита , диаграммой Мизухаши ( диаграмма Мизухаши ), диаграммой Мизухаши-Смита ( диаграмма Мизухаши Смита ), Volpert–Smith chart ( Диаграмма Вольперта—Смита ) или диаграмма Мизухаши-Вольперта-Смита ) — графический калькулятор или номограмма, предназначенная для инженеров-электриков и электронщиков, специализирующихся на радиочастотной (РЧ) технике, для помощи в решении проблем с линиями передачи и согласующими цепями.

Это было независимо предложен Тосаку Мизухаси в 1937 году . и Amiel R. Volpert ( Амиэль Р. Волперт ) и Филип Х. Смит в 1939 году. Начав с прямоугольной диаграммы, Смит к 1936 году разработал специальную карту полярных координат , которая при участии его коллег Еноха Б. Феррелла и Джеймса У. Макрея , знакомых с конформными отображениями , была переработана в окончательную форму в начале 1937 г., которая в конечном итоге была опубликована в январе 1939 г. Первоначально Смит называл это « линейной диаграммой передачи ». и другие авторы впервые использовали такие названия, как « диаграмма отражения », « круговая диаграмма импеданса », « диаграмма иммитанса » или « диаграмма Z-плоскости ». первые последователи технологического института Массачусетского Радиационной лаборатории в 1940-х годах начали называть ее просто « диаграммой Смита ». имя, общепринятое в западном мире к 1950 году.

Диаграмму Смита можно использовать для одновременного отображения нескольких параметров, включая импедансы , адмиттансы , коэффициенты отражения и т.д. $S_{nn}\,$ параметры рассеяния , кружки коэффициента шума , контуры постоянного усиления и области безусловной устойчивости . Диаграмма Смита чаще всего используется в области единичного радиуса или внутри нее . Однако оставшаяся часть по-прежнему математически актуальна и используется, например, при проектировании генераторов и устойчивости . анализе Хотя использование бумажных диаграмм Смита для решения сложных математических задач, связанных с сопоставлением, было в значительной степени заменено программными методами, диаграмма Смита по-прежнему остается очень полезным методом отображения. как радиочастотные параметры ведут себя на одной или нескольких частотах, альтернатива использованию табличной информации. Таким образом, большая часть программного обеспечения для анализа радиочастотных цепей включает опцию диаграммы Смита для отображения результатов, и все, кроме самых простых приборов для измерения импеданса, могут отображать измеренные результаты на дисплее диаграммы Смита.

Диаграмма импеданса Смита (без нанесения данных)

Обзор

Сетевой анализатор ( HP 8720A), показывающий диаграмму Смита.

Диаграмма Смита представляет собой математическое преобразование двумерной декартовой комплексной плоскости. Комплексные числа с положительными действительными частями отображаются внутри круга. Те, у кого отрицательные действительные части, находятся за пределами круга.Если мы имеем дело только с импедансами с неотрицательными резистивными компонентами, наш интерес сосредоточен на области внутри круга.Преобразование для диаграммы Смита импеданса выглядит следующим образом:

$\Gamma ={\frac {Z-Z_{0}}{Z+Z_{0}}}={\frac {z-1}{z+1}},$

где $z={\frac {Z}{Z_{0}}},$ т. е. комплексный импеданс, $Z,$ нормированный по эталонному сопротивлению, $Z_{0}$. Диаграмма импеданса Смита представляет собой график Аргана преобразованных таким образом импедансов. Импедансы с неотрицательными резистивными компонентами появятся внутри круга с единичным радиусом; начало координат будет соответствовать эталонному сопротивлению, $Z_{0}$.

Диаграмма Смита строится на плоскости комплексного коэффициента отражения в двух измерениях и может быть масштабирована по нормализованному импедансу (наиболее распространенному), нормализованному адмиттансу или тому и другому, используя разные цвета, чтобы различать их. Их часто называют диаграммами Z, Y и YZ Смита соответственно. Нормализованное масштабирование позволяет использовать диаграмму Смита для решения задач, связанных с любой характеристикой или сопротивлением системы, которое представлено центральной точкой диаграммы. Наиболее часто используемый нормировочный импеданс составляет 50 Ом . Как только ответ получен с помощью графических конструкций, описанных ниже, можно легко преобразовать нормализованное полное сопротивление (или нормализованную проводимость) в соответствующее ненормализованное значение путем умножения на характеристическое сопротивление (адмиттанс). Коэффициенты отражения можно прочитать прямо из диаграммы, поскольку они являются безразмерными параметрами.

Диаграмма Смита имеет шкалу по окружности или периферии, которая градуирована в длинах волн и градусах . Шкала длин волн используется в задачах с распределенными компонентами и представляет собой расстояние, измеренное вдоль линии передачи, соединенной между генератором или источником и нагрузкой, до рассматриваемой точки. Градусная шкала представляет собой угол коэффициента отражения напряжения в этой точке. Диаграмма Смита также может использоваться для сосредоточенных элементов задач сопоставления и анализа .

Использование диаграммы Смита и интерпретация полученных с ее помощью результатов требует хорошего понимания теории цепей переменного тока и теории линий передачи, которые являются необходимыми условиями для радиочастотных инженеров.

Поскольку импедансы и адмиттансы изменяются в зависимости от частоты, проблемы с использованием диаграммы Смита можно решать только вручную, используя одну частоту за раз, а результат обозначается точкой . Этого часто бывает достаточно для узкополосных приложений (обычно примерно до 5–10% ), но для более широких полос обычно необходимо применять методы диаграммы Смита на более чем одной частоте в рабочем диапазоне частот. При условии, что частоты достаточно близки, полученные точки диаграммы Смита можно соединить прямыми линиями для создания локуса .

Местоположение точек на диаграмме Смита, охватывающее диапазон частот, можно использовать для визуального представления:

• насколько емкостной или индуктивной является нагрузка в диапазоне частот
• насколько трудным может быть согласование на разных частотах
• насколько хорошо подобран тот или иной компонент.

Точность диаграммы Смита снижается для задач, связанных с большим количеством импедансов или адмиттансов, хотя масштабирование может быть увеличено для отдельных областей, чтобы учесть это.

Математическая основа

Самое простое использование диаграммы Смита импеданса. Волна распространяется по линии передачи с характеристическим сопротивлением Z ₀ и заканчивается на нагрузке с сопротивлением Z _L и нормированным сопротивлением z = Z _L / Z ₀ . Имеет место отражение сигнала с коэффициентом Γ. Каждая точка на диаграмме Смита одновременно представляет как значение z (внизу слева), так и соответствующее значение Γ (внизу справа), связанное соотношением z = (1 + Γ)/(1 - Γ).

Фактический и нормированный импеданс и адмиттанс

Линия передачи с характеристическим сопротивлением $Z_{0}\,$ можно повсеместно считать имеющим характерный допуск $Y_{0}\,$ где

$Y_{0}={\frac {1}{Z_{0}}}\,$

Любой импеданс, $Z_{\text{T}}\,$ Выраженный в Омах, его можно нормализовать путем деления его на характеристическое сопротивление, поэтому нормализованное сопротивление с использованием строчной буквы z _T определяется выражением

$z_{\text{T}}={\frac {Z_{\text{T}}}{Z_{0}}}\,$

Аналогично, для нормированного допуска

$y_{\text{T}}={\frac {Y_{\text{T}}}{Y_{0}}}\,$

Единицей системе СИ импеданса в является ом с символом заглавной греческой буквы омега (Ом), а — СИ единицей проводимости сименс с символом заглавной буквы S. Нормализованный импеданс и нормализованная адмиттанция безразмерны . Фактические импедансы и адмиттансы необходимо нормализовать, прежде чем использовать их на диаграмме Смита. После получения результата его можно денормализовать для получения фактического результата.

Диаграмма Смита нормализованного импеданса

Линии электропередачи прерваны обрывом цепи (вверху) и коротким замыканием (внизу). Импульс прекрасно отражается от обоих этих выводов, но знак отраженного напряжения в обоих случаях противоположный. Черные точки представляют электроны, а стрелки показывают электрическое поле.

Используя теорию линий передачи, если линия передачи заканчивается импедансом ( $Z_{\text{T}}\,$), который отличается от его характеристического сопротивления ( $Z_{0}\,$), равнодействующей на линии, состоящей из и как падающей, так прямой ( $V_{\text{F}}\,$) и отраженный или перевернутый ( $V_{\text{R}}\,$) волны. Используя сложную экспоненциальную запись:

$V_{\text{F}}=A\exp(j\omega t)\exp(+\gamma \ell )~\,$ и

$V_{\text{R}}=B\exp(j\omega t)\exp(-\gamma \ell )\,$

где

$\exp(j\omega t)\,$ это временная часть волны

$\exp(\pm \gamma \ell )\,$ – пространственная часть волны и

$\omega =2\pi f\,$ где

$\omega \,$ угловая частота в радианах в секунду (рад/с)

$f\,$ частота ( Гц в герцах )

$t\,$ это время в секундах (с)

$A\,$ и $B\,$ константы ​

$\ell \,$ — расстояние, измеренное вдоль линии электропередачи от нагрузки до генератора в метрах (м)

Также

$\gamma =\alpha +j\beta \,$ - постоянная распространения , измеряемая в единицах СИ радиан / метр.

где

$\alpha \,$ — константа затухания в неперах на метр (Нп/м).

$\beta \,$ фазовая постоянная в радианах на метр (рад/м).

Диаграмма Смита используется с одной частотой ( $\omega$) одновременно и только на один момент ( $t$) одновременно, поэтому временная часть фазы ( $\exp(j\omega t)\,$) фиксировано. Все члены на самом деле умножаются на это, чтобы получить мгновенную фазу , но это общепринято и подразумевается, что ее опускают. Поэтому,

$V_{\text{F}}=A\exp(+\gamma \ell )\,$ и

$V_{\text{R}}=B\exp(-\gamma \ell )\,$

где $A\,$ и $B\,$ – соответственно амплитуды прямого и обратного напряжения на нагрузке.

Изменение комплексного коэффициента отражения в зависимости от положения вдоль линии

Взгляд в сторону груза по длине $\ell \,$ линии передачи без потерь, импеданс изменяется как $\ell \,$ увеличивается, следуя за синим кружком. (Этот импеданс характеризуется коэффициентом отражения $V_{\text{reflected}}/V_{\text{incident}}$.) Синий круг, расположенный в центре диаграммы импеданса Смита, иногда называют кругом КСВ (сокращение от постоянного коэффициента стоячей волны ).

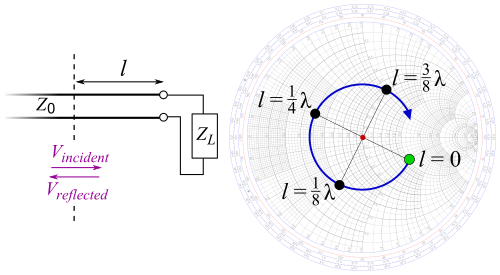
Комплексный коэффициент отражения напряжения $\Gamma \,$ определяется как отношение отраженной волны к падающей (или прямой) волне. Поэтому,

$\Gamma ={\frac {V_{\text{R}}}{V_{\text{F}}}}={\frac {B\exp(-\gamma \ell )}{A\exp(+\gamma \ell )}}=C\exp(-2\gamma \ell )\,$

где C также является константой.

Для однородной линии передачи (в которой $\gamma \,$ постоянна), комплексный коэффициент отражения стоячей волны меняется в зависимости от положения на линии. Если линия с потерями ( $\alpha \,$ не равно нулю), это представлено на диаграмме Смита спиральной траекторией. Однако в большинстве задач на диаграмме Смита потери можно считать незначительными ( $\alpha =0\,$) и задача их решения существенно упрощается. Таким образом, для случая без потерь выражение для комплексного коэффициента отражения принимает вид

$\Gamma =\Gamma _{\text{L}}\exp(-2j\beta \ell )\,$

где $\Gamma _{\text{L}}\,$ - коэффициент отражения на нагрузке, а $\ell \,$ — длина линии от нагрузки до места измерения коэффициента отражения. Фазовая постоянная $\beta \,$ также может быть записано как

$\beta ={\frac {2\pi }{\lambda }}\,$

где $\lambda \,$ — длина волны в линии передачи на тестовой частоте.

Поэтому,

$\Gamma =\Gamma _{\text{L}}\exp \left({\frac {-4j\pi }{\lambda }}\ell \right)\,$

Это уравнение показывает, что для стоячей волны комплексный коэффициент отражения и импеданс повторяются каждую половину длины волны вдоль линии передачи. Комплексный коэффициент отражения обычно называют просто коэффициентом отражения. Внешняя окружная шкала диаграммы Смита представляет собой расстояние от генератора до нагрузки, выраженное в длинах волн, и поэтому масштабируется от нуля до 0,50.

Изменение нормированного импеданса в зависимости от положения вдоль линии

Если $\,V\,$ и $\,I\,$ - напряжение на поперечном напряжении и ток, входящий в оконечную нагрузку в конце линии передачи соответственно, тогда

$V_{\mathsf {F}}+V_{\mathsf {R}}=V\,$

и

$V_{\mathsf {F}}-V_{\mathsf {R}}=Z_{0}\,I\,$.

Разделив эти уравнения и подставив оба коэффициента отражения напряжения

$\Gamma ={\frac {V_{\mathsf {R}}}{\,V_{\mathsf {F}}\,}}\,$

и нормализованное полное сопротивление нагрузки, представленное строчной буквой z , индекс T

$z_{\mathsf {T}}={\frac {V}{\,Z_{0}\,I\,}}\,$

дает результат:

$z_{\mathsf {T}}={\frac {1+\Gamma }{\,1-\Gamma \,}}\,.$

Альтернативно, с точки зрения коэффициента отражения

$\Gamma ={\frac {z_{\mathsf {T}}-1}{\,z_{\mathsf {T}}+1\,}}\,$

Это уравнения, которые используются для построения диаграммы Z Смита. Математически говоря $\,\Gamma \,$ и $\,z_{\mathsf {T}}\,$ связаны преобразованием Мёбиуса .

Оба $\,\Gamma \,$ и $\,z_{\mathsf {T}}\,$ выражаются комплексными числами без каких-либо единиц. Оба они изменяются в зависимости от частоты, поэтому для любого конкретного измерения необходимо указывать частоту, на которой оно проводилось, вместе с характеристическим сопротивлением.

$\,\Gamma \,$ может быть выражено в величине и угле на полярной диаграмме . Любой фактический коэффициент отражения должен иметь величину меньше или равную единице , поэтому на тестовой частоте это может быть выражено точкой внутри круга единичного радиуса. Диаграмма Смита фактически построена на такой полярной диаграмме. Масштабирование диаграммы Смита разработано таким образом, что коэффициент отражения можно преобразовать в нормализованное сопротивление или наоборот. Используя диаграмму Смита, нормированный импеданс можно получить с достаточной точностью, нанося на график точку, представляющую коэффициент отражения, рассматривая диаграмму Смита как полярную диаграмму , а затем считывая ее значение непосредственно с использованием характеристического масштабирования диаграммы Смита. Этот метод является графической альтернативой подстановке значений в уравнения.

Подставив выражение, как изменяется коэффициент отражения вдоль несогласованной линии передачи без потерь

$\Gamma ={\frac {B\exp(-\gamma \ell )}{A\exp(\gamma \ell )}}={\frac {B\exp(-j\beta \ell )}{A\exp(j\beta \ell )}}\,$

для случая без потерь в уравнение для нормированного импеданса через коэффициент отражения

$z_{\mathsf {T}}={\frac {1+\Gamma }{\,1-\Gamma \,}}\,.$

и используя формулу Эйлера

$\exp(j\theta )={\text{cis}}\,\theta =\cos \theta +j\,\sin \theta \,$

дает уравнение линии передачи импедансной версии для случая без потерь:

$Z_{\mathsf {in}}=Z_{0}{\frac {\,Z_{\mathsf {L}}+j\,Z_{0}\tan(\beta \ell )\,}{\,Z_{0}+j\,Z_{\mathsf {L}}\tan(\beta \ell )\,}}\,$

где $\,Z_{\mathsf {in}}\,$ - это импеданс, «видимый» на входе линии передачи без потерь длиной $\,\ell \,,$ завершено с импедансом $\,Z_{\mathsf {L}}\,$

Версии уравнения линии передачи могут быть получены аналогичным образом для случая отсутствия потерь на проводимость и для случаев импеданса и потерь на проводимость.

Графический эквивалент диаграммы Смита использования уравнения линии передачи состоит в нормализации $\,Z_{\mathsf {L}}\,,$ чтобы нанести полученную точку на диаграмму Z Смита и нарисовать круг через эту точку с центром в центре диаграммы Смита. Путь по дуге круга показывает, как изменяется сопротивление при движении по линии передачи. В этом случае необходимо использовать окружное масштабирование (длину волны), помня, что это длина волны внутри линии передачи и может отличаться от длины волны в свободном пространстве.

Области диаграммы Z Смита

Если полярная диаграмма отображается в декартовой системе координат, принято измерять углы относительно положительной оси X , используя направление против часовой стрелки для положительных углов. Величина комплексного числа — это длина прямой линии, проведенной от начала координат до представляющей его точки. В диаграмме Смита используется то же соглашение, при этом отмечается, что в плоскости нормализованного импеданса положительная ось X проходит от центра диаграммы Смита в точке $\,z_{\mathsf {T}}=1\pm j0\,$ в точку $\,z_{\mathsf {T}}=\infty \pm j\infty \,.$ Область над осью x представляет индуктивные импедансы (положительные мнимые части), а область под осью x представляет собой емкостные сопротивления (отрицательные мнимые части).

Если окончание идеально согласовано, коэффициент отражения будет равен нулю, что фактически представлено кругом нулевого радиуса или фактически точкой в ​​центре диаграммы Смита. Если бы завершение представляло собой совершенно разомкнутую цепь или короткое замыкание, величина коэффициента отражения была бы равна единице, вся мощность была бы отражена, и точка лежала бы в некоторой точке на единичной окружности.

Круги постоянного нормированного сопротивления и постоянного нормированного реактивного сопротивления

Диаграмма Смита нормированного импеданса состоит из двух семейств кругов: кругов постоянного нормированного сопротивления и кругов постоянного нормированного реактивного сопротивления. В плоскости комплексного коэффициента отражения диаграмма Смита занимает круг единичного радиуса с центром в начале координат. Таким образом, в декартовых координатах окружность будет проходить через точки (+1,0) и (−1,0) на оси x и точки (0,+1) и (0,−1) на y оси . .

Поскольку оба $\,\Gamma \,$ и $\,z_{\mathsf {T}}\,$ являются комплексными числами, в общем случае их можно записать как:

$z_{\mathsf {T}}=a+jb\,$

$~\Gamma ~=c+jd\,$

с действительными числами a , b , c и d .

Подставив их в уравнение, связывающее нормализованный импеданс и комплексный коэффициент отражения:

$\Gamma ={\frac {z_{\mathsf {T}}-1}{\,z_{\mathsf {T}}+1\,}}={\frac {(a-1)+j\,b}{\,(a+1)+j\,b\,}}\,$

дает следующий результат:

$\Gamma =c+jd=\left[{\frac {a^{2}+b^{2}-1}{\,(a+1)^{2}+b^{2}\,}}\right]+j\left[{\frac {2b}{\,(a+1)^{2}+b^{2}\,}}\right]=\left[1+{\frac {-2(a+1)}{\,(a+1)^{2}+b^{2}\,}}\right]+j\left[{\frac {+2b}{\,(a+1)^{2}+b^{2}\,}}\right]\,.$

Это уравнение описывает, как комплексный коэффициент отражения изменяется с нормализованным импедансом, и его можно использовать для построения обоих семейств окружностей.

Диаграмма И. Смита

Диаграмма Y Смита построена аналогично диаграмме Z Смита, но путем выражения значений коэффициента отражения напряжения через нормированный адмиттанс, а не через нормированный импеданс. Нормализованная проводимость y _T является обратной величиной нормированного импеданса z _T , поэтому

$y_{\mathsf {T}}={\frac {1}{z_{\mathsf {T}}}}\,$

Поэтому:

$y_{\mathsf {T}}={\frac {1-\Gamma }{\,1+\Gamma \,}}\,$

и

$\Gamma ={\frac {1-y_{\mathsf {T}}}{\,1+y_{\mathsf {T}}\,}}\,$

Диаграмма Y Смита выглядит как нормализованный импеданс, но с графическими вложенными кружками, повернутыми на 180°, а числовая шкала остается в том же положении (не повернутой), что и Z. диаграмма

Аналогично принимая

$y_{\mathsf {T}}={\tilde {o}}+j\,{\tilde {p}}\,$

серьезно ​ $\,{\tilde {o}}\,$ и $\,{\tilde {p}}\,$ дает аналогичный результат, хотя и с большим количеством и другими знаками минус:

$\Gamma =c+jd=\left[{\frac {1-{\tilde {o}}^{2}-{\tilde {p}}^{2}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]+j\left[{\frac {-2{\tilde {p}}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]=\left[{\frac {2({\tilde {o}}+1)}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}-1\right]+j\left[{\frac {-2{\tilde {p}}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]\,.$

Область над осью x представляет емкостные проводимости, а область под осью x представляет индуктивные проводимости. Емкостные адмиттансы имеют положительную мнимую часть, а индуктивные адмиттансы имеют отрицательную мнимую часть.

Опять же, если окончание идеально согласовано, коэффициент отражения будет равен нулю, что представлено «кругом» нулевого радиуса или фактически точкой в ​​центре диаграммы Смита. Если бы оконечная нагрузка была совершенно разомкнутой или короткозамкнутой, величина коэффициента отражения напряжения была бы равна единице, вся мощность была бы отражена, и точка лежала бы в некоторой точке на единичном круге диаграммы Смита.

Практические примеры

Примеры точек, нанесенных на диаграмму Смита нормализованного импеданса

Точка с коэффициентом отражения 0,63 и углом 60°, представленная в полярной форме как $0.63\angle 60^{\circ }\,$, отображается как точка P ₁ на диаграмме Смита. Чтобы построить это, можно использовать шкалу окружных углов (коэффициента отражения), чтобы найти $\angle 60^{\circ }\,$ градуировка и линейка, чтобы провести линию, проходящую через нее и центр диаграммы Смита. Затем длина линии будет масштабирована до P _1, если предположить, что радиус диаграммы Смита равен единице. Например, если фактический радиус, измеренный от бумаги, составлял 100 мм, длина OP ₁ будет равна 63 мм.

В следующей таблице приведены некоторые аналогичные примеры точек, нанесенных на диаграмму Z Смита. Для каждого коэффициент отражения задается в полярной форме вместе с соответствующим нормализованным импедансом в прямоугольной форме. Преобразование можно считать непосредственно из диаграммы Смита или путем подстановки в уравнение.

Некоторые примеры точек, нанесенных на диаграмму Смита нормированного импеданса

Идентификация точки	Коэффициент отражения (полярная форма)	Нормализованный импеданс (прямоугольная форма)
П 1 (индуктивный)	$0.63\angle 60^{\circ }\,$	$0.80+j1.40\,$
П 2 (индуктивный)	$0.73\angle 125^{\circ }\,$	$0.20+j0.50\,$
П 3 (емкостный)	$0.44\angle -116^{\circ }\,$	$0.50-j0.50\,$

Работа как с диаграммой Z Smith, так и с диаграммой Y Smith.

В радиочастотных цепях и задачах согласования иногда удобнее работать с адмиттансами (представляющими проводимость и проводимость ), а иногда удобнее работать с импедансами (представляющими сопротивления и реактивные сопротивления ). Решение типичной задачи согласования часто требует внесения некоторых изменений в оба типа диаграммы Смита с использованием нормализованного импеданса для последовательных элементов и нормализованных проводимостей для параллельных элементов. Для этого можно использовать двойную (нормализованную) диаграмму Смита импеданса и проводимости. В качестве альтернативы можно использовать один тип и при необходимости преобразовать масштаб в другой. Чтобы перейти от нормированного импеданса к нормированному адмиттансу или наоборот, точка, представляющая значение рассматриваемого коэффициента отражения, перемещается точно на 180 градусов по тому же радиусу. Например, точка P1 в примере представляет коэффициент отражения $0.63\angle 60^{\circ }\,$ имеет нормированный импеданс $z_{P}=0.80+j1.40\,$. Чтобы графически изменить это на эквивалентную нормализованную точку допуска, скажем, Q1, с помощью линейки рисуют линию от P1 через центр диаграммы Смита до Q1, равного радиуса в противоположном направлении. Это эквивалентно перемещению точки по круговой траектории ровно на 180 градусов. Чтение значения из диаграммы Смита для Q1, помня, что масштабирование теперь находится в нормализованном адмиттанте, дает $y_{P}=0.30-j0.54\,$. Выполнение расчета

$y_{\text{T}}={\frac {1}{z_{\text{T}}}}\,$

вручную подтвердит это.

После преобразования выполнения импеданса в адмиттанс масштабирование меняется на нормализованный адмиттанс до тех пор, пока не будет выполнено позднее преобразование обратно в нормализованный импеданс.

В таблице ниже показаны примеры нормализованных импедансов и их эквивалентных нормализованных адмиттансов, полученных поворотом точки на 180 °. Опять же, их можно получить либо путем расчета, либо с использованием диаграммы Смита, как показано, путем преобразования нормализованных плоскостей импеданса и нормализованных адмиттансов.

Значения коэффициента отражения как нормированные импедансы и эквивалентные нормированные адмиттансы

Нормализованная плоскость импеданса	Нормализованная плоскость допуска
П 1 ( $z=0.80+j1.40\,$)	Вопрос 1 ( $y=0.30-j0.54\,$)
П 10 ( $z=0.10+j0.22\,$)	Вопрос 10 ( $y=1.80-j3.90\,$)

Значения комплексного коэффициента отражения, нанесенные на диаграмму Смита нормированного импеданса, и их эквиваленты на диаграмме Смита нормированного полного сопротивления

Выбор типа диаграммы Смита и типа компонента

Выбор того, использовать ли диаграмму Z Смита или диаграмму Y Смита для того или иного конкретного расчета, зависит от того, что удобнее. Импедансы при последовательном соединении и адмиттансы при параллельном соединении складываются, тогда как импедансы при параллельном соединении и адмиттансы при последовательном соединении связаны обратным уравнением. Если $Z_{\text{TS}}$ - эквивалентный импеданс последовательных импедансов и $Z_{\text{TP}}$ - эквивалентный импеданс параллельных импедансов, тогда

$Z_{\text{TS}}=Z_{1}+Z_{2}+Z_{3}+...\,$

${\frac {1}{Z_{\text{TP}}}}={\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+{\frac {1}{Z_{3}}}+...\,$

Для допусков верно обратное, т.е.

$Y_{\text{TP}}=Y_{1}+Y_{2}+Y_{3}+...\,$

${\frac {1}{Y_{\text{TS}}}}={\frac {1}{Y_{1}}}+{\frac {1}{Y_{2}}}+{\frac {1}{Y_{3}}}+...\,$

Работа с обратными величинами , особенно с комплексными числами, требует больше времени и подвержена ошибкам, чем использование линейного сложения. Таким образом, в целом большинство радиоинженеров работают в плоскости, где топография схемы поддерживает линейное сложение. В следующей таблице приведены комплексные выражения для импеданса (действительного и нормализованного) и адмиттанса (действительного и нормализованного) для каждого из трех основных элементов пассивной цепи : сопротивления, индуктивности и емкости. Используя только характеристическое сопротивление (или характеристическую проводимость) и испытательную частоту, можно найти эквивалентную схему , и наоборот.

Выражения для импеданса и адмиттанса
нормализовано по импедансу Z ₀ или адмиттансу Y ₀

Тип элемента	Импеданс ( Z или z ) или реактивное сопротивление ( X или x )		Адмиттанс ( Y или y ) или проводимость ( B или b )
	Действительный ( Ой )	Нормализованный (нет единиц)	Действительный ( С )	Нормализованный (нет единиц)
Сопротивление ( Р )	$\;Z=R\;$	$\;z={\frac {R}{Z_{0}}}=RY_{0}\;$	$\;Y=G={\frac {1}{R}}\;$	$\;y=g={\frac {1}{RY_{0}}}={\frac {Z_{0}}{R}}\;$
Индуктивность ( Л )	$\;Z=jX_{\text{L}}=j\omega L\;$	$\;z=jx_{\text{L}}=j{\frac {\omega L}{Z_{0}}}=j\omega LY_{0}\;$	$\;Y=-jB_{\text{L}}={\frac {-j}{\omega L}}\;$	$\;y=-jb_{\text{L}}={\frac {-j}{\omega LY_{0}}}={\frac {-jZ_{0}}{\omega L}}\;$
Емкость ( С )	$\;Z=-jX_{\text{C}}={\frac {-j}{\omega C}}\;$	$\;z=-jx_{\text{C}}={\frac {-j}{\omega CZ_{0}}}={\frac {-jY_{0}}{\omega C}}\;$	$\;Y=jB_{\text{C}}=j\omega C\;$	$\;y=jb_{\text{C}}=j{\frac {\omega C}{Y_{0}}}=j\omega CZ_{0}\;$

Использование диаграммы Смита для решения задач сопряженного сопоставления с распределенными компонентами

Распределенное согласование становится возможным и иногда требуется, когда физический размер согласующих компонентов составляет более примерно 5% длины волны на рабочей частоте. При этом электрическое поведение многих сосредоточенных компонентов становится весьма непредсказуемым. Это происходит в микроволновых цепях, а также когда для высокой мощности требуются большие компоненты в коротковолновом, FM- и телевещании.

Для распределенных компонентов необходимо учитывать влияние на коэффициент отражения и полное сопротивление перемещения по линии передачи с использованием внешней окружной шкалы диаграммы Смита, откалиброванной по длинам волн.

В следующем примере показано, как линия передачи, оканчивающаяся произвольной нагрузкой, может быть согласована на одной частоте с последовательным или параллельным реактивным компонентом, в каждом случае подключенным в определенных положениях.

Построение диаграммы Смита для некоторого сопоставления распределенных линий передачи

Предположим, что имеется воздушная линия передачи с характеристическим сопротивлением без потерь. $Z_{0}=50\ \Omega$, работающий на частоте 800 МГц, оканчивается цепью, состоящей из 17,5 $\Omega$ резистор последовательно с катушкой индуктивности 6,5 наногенри (6,5 нГн). Как можно совместить линию?

Из приведенной выше таблицы реактивное сопротивление дросселя, входящего в оконечную нагрузку, на частоте 800 МГц равно:

$Z_{L}=j\omega L=j2\pi fL=j32.7\ \Omega \,$

поэтому импеданс комбинации ( $Z_{T}$) определяется

$Z_{T}=17.5+j32.7\ \Omega \,$

и нормированный импеданс ( $z_{T}$) является

$z_{T}={\frac {Z_{T}}{Z_{0}}}=0.35+j0.65\,$

Это нанесено на диаграмму Z Смита в точке P ₂₀ . Линия OP ₂₀ продолжается до шкалы длин волн, где она пересекается в точке $L_{1}=0.098\lambda \,$. проводится круг с центром в центре диаграммы Смита, _{Поскольку линия передачи не имеет потерь, через точку P 20} чтобы представить путь коэффициента отражения постоянной величины из-за прерывания. В точке Р ₂₁ окружность пересекается с единичной окружностью постоянного нормированного сопротивления при

$z_{P21}=1.00+j1.52\,$.

Продолжение линии OP ₂₁ пересекает шкалу длин волн при $L_{2}=0.177\lambda \,$, поэтому расстояние от окончания до этой точки на линии определяется выражением

$L_{2}-L_{1}=0.177\lambda -0.098\lambda =0.079\lambda \,$

Поскольку линия передачи разнесена по воздуху, длина волны на частоте 800 МГц в линии такая же, как и в свободном пространстве, и определяется выражением

$\lambda ={\frac {c}{f}}\,$

где $c\,$ – скорость электромагнитного излучения в свободном пространстве и $f\,$ — частота в герцах. Результат дает $\lambda =375\ \mathrm {mm} \,$, делая положение согласующего компонента на расстоянии 29,6 мм от нагрузки.

Сопряженное согласование импеданса на P ₂₁ ( $z_{match}\,$) является

$z_{match}=-j(1.52),\!$

Поскольку диаграмма Смита все еще находится в плоскости нормированного импеданса, из таблицы выше следует, что последовательный конденсатор $C_{m}\,$ требуется там, где

$z_{match}=-j1.52={\frac {-j}{\omega C_{m}Z_{0}}}={\frac {-j}{2\pi fC_{m}Z_{0}}}\,$

Переставляя, получаем

$C_{m}={\frac {1}{(1.52)\omega Z_{0}}}={\frac {1}{(1.52)(2\pi f)Z_{0}}}$.

Замена известных значений дает

$C_{m}=2.6\ \mathrm {pF} \,$

Чтобы согласование согласования на частоте 800 МГц, последовательный конденсатор емкостью 2,6 пФ должен быть установлен последовательно с линией передачи на расстоянии 29,6 мм от окончания.

Альтернативное согласование шунта можно рассчитать после выполнения преобразования диаграммы Смита от нормализованного импеданса к нормализованному адмиттансу. Точка Q ₂₀ эквивалентна P ₂₀ , но выражена как нормализованная проводимость. Чтение масштаба диаграммы Смита с учетом того, что теперь это нормализованный допуск, дает

$y_{Q20}=0.65-j1.20\,$

(На самом деле это значение фактически не используется). Однако продолжение линии OQ ₂₀ до шкалы длин волн дает $L_{3}=0.152\lambda \,$. Самая ранняя точка, в которой может быть введено сопряженное шунтирующее согласование, движущееся к генератору, будет в Q ₂₁ , то же положение, что и предыдущий P ₂₁ , но на этот раз представляющее нормализованную проводимость, определяемую выражением

$y_{Q21}=1.00+j1.52\,$.

Расстояние вдоль линии передачи в этом случае составляет

$L_{2}+L_{3}=0.177\lambda +0.152\lambda =0.329\lambda \,$

который преобразуется в 123 мм.

Компонент сопряженного согласования должен иметь нормализованный адмиттанс ( $y_{match}$) из

$y_{match}=-j1.52\,$.

Из таблицы видно, что для отрицательной проводимости потребуется дроссель, подключенный параллельно линии передачи. Если его значение $L_{m}\,$, затем

$-j1.52={\frac {-j}{\omega L_{m}Y_{0}}}={\frac {-jZ_{0}}{2\pi fL_{m}}}\,$

Это дает результат

$L_{m}=6.5\ \mathrm {nH} \,$

Таким образом, подходящим индуктивным шунтом будет дроссель 6,5 нГн, включенный параллельно линии и расположенный на расстоянии 123 мм от нагрузки.

Использование диаграммы Смита для анализа схем с сосредоточенными элементами

Анализ компонентов с сосредоточенными элементами предполагает, что длина волны на рабочей частоте значительно превышает размеры самих компонентов. Диаграмма Смита может использоваться для анализа таких цепей, и в этом случае движения вокруг диаграммы генерируются (нормализованными) импедансами и адмиттанами компонентов на рабочей частоте. В этом случае масштабирование длины волны по окружности диаграммы Смита не используется. Следующая схема будет проанализирована с использованием диаграммы Смита на рабочей частоте 100 МГц. На этой частоте длина волны в свободном пространстве составляет 3 м. Размеры самих компонентов будут порядка миллиметров, поэтому предположение о сосредоточенных компонентах будет справедливым. Несмотря на отсутствие линии передачи как таковой, все равно необходимо определить полное сопротивление системы, чтобы можно было выполнить расчеты нормализации и денормализации, а также $Z_{0}=50\ \Omega \,$ здесь хороший выбор, так как $R_{1}=50\ \Omega \,$. Если бы существовали очень разные значения сопротивления, лучшим выбором было бы значение, близкое к этому.

Схема с сосредоточенными элементами, которую можно проанализировать с помощью диаграммы Смита.

Диаграмма Смита с графическим построением для анализа цепи с сосредоточенными параметрами

Анализ начинается с диаграммы Z Смита, в которой рассматривается только R ₁ , без каких-либо других компонентов. Как $R_{1}=50\ \Omega \,$ совпадает с импедансом системы и обозначается точкой в ​​центре диаграммы Смита. Первое преобразование - это ОП ₁ по линии постоянного нормированного сопротивления, в данном случае добавление нормированного реактивного сопротивления - j 0,80, что соответствует последовательному конденсатору емкостью 40 пФ. Точки с суффиксом P находятся в плоскости Z , а точки с суффиксом Q — в Y. плоскости Следовательно, преобразования P ₁ в Q ₁ и P ₃ в Q ₃ происходят из диаграммы Z Смита в диаграмму Y Смита, а преобразования Q ₂ в P ₂ происходят из диаграммы Y Смита в диаграмму Z Смита. В следующей таблице показаны шаги, предпринятые для работы с оставшимися компонентами и преобразованиями, которые в конечном итоге возвращаются к центру диаграммы Смита и к идеальному согласованию 50 Ом.

Этапы диаграммы Смита для анализа схемы с сосредоточенными элементами

Трансформация	Самолет	x или b Нормализованное значение	Емкость/Индуктивность	Формула для решения	Результат
$O\rightarrow P_{1}\,$	$Z\,$	$-j0.80\,$	Емкость (серия)	$-j0.80={\frac {-j}{\omega C_{1}Z_{0}}}\,$	$C_{1}=40\ \mathrm {pF} \,$
$Q_{1}\rightarrow Q_{2}\,$	$Y\,$	$-j1.49\,$	Индуктивность (шунт)	$-j1.49={\frac {-j}{\omega L_{1}Y_{0}}}\,$	$L_{1}=53\ \mathrm {nH} \,$
$P_{2}\rightarrow P_{3}\,$	С	$-j0.23\,$	Емкость (серия)	$-j0.23={\frac {-j}{\omega C_{2}Z_{0}}}\,$	$C_{2}=138\ \mathrm {pF} \,$
$Q_{3}\rightarrow O\,$	И	$+j1.14\,$	Емкость (шунт)	$+j1.14={\frac {j\omega C_{3}}{Y_{0}}}\,$	$C_{3}=36\ \mathrm {pF} \,$

3D-диаграмма Смита

Трехмерное представление диаграммы Смита

Обобщение диаграммы Смита на трехмерную сферу, основанное на расширенной комплексной плоскости ( сфера Римана ) и инверсной геометрии , было предложено Мюллером и др. в 2011 году.

Схема объединяет пассивную и активную схему на маленьких и больших кругах на поверхности единичной сферы, используя стереографическую конформную карту обобщенной плоскости коэффициента отражения. Учитывая точку на бесконечности, пространство новой карты включает в себя все возможные нагрузки: северный полюс — идеально совмещенная точка, а южный полюс — полностью несовпадающая точка.

Трехмерная диаграмма Смита была расширена за пределы сферической поверхности для отображения различных скалярных параметров, таких как групповая задержка, коэффициенты качества или ориентация частоты. Визуальная ориентация частоты (по часовой стрелке и против часовой стрелки) позволяет различать отрицательные / емкостные и положительные / индуктивные, коэффициенты отражения которых одинаковы при нанесении на двумерную диаграмму Смита, но чьи ориентации расходятся по мере увеличения частоты.

См. также

• Бинарная мозаика
• График Боде
• сюжет Найквиста
• Круговая диаграмма Хейланда-Осанны
• цис (математика)
• Поперечное (приборостроение)

Дальнейшее чтение

• Кэмпбелл, Джордж Эшли (апрель 1911 г.). «Цисоидальные колебания» (PDF) . Труды Американского института инженеров-электриков . ХХХ (1–6). Американский институт инженеров-электриков : 789–824 [Рис. 13 на стр. 810]. дои : 10.1109/PAIEE.1911.6659711 . S2CID   51647814 . Проверено 24 июня 2023 г. (37 страниц) (Примечание. Включает раннее графическое изображение чего-то похожего на диаграмму Смита за десятилетия до того, как Мизухаси, Вольперт и Смит опубликовали свои работы.)
• Флеминг, Джон Амброуз (январь 1912 г.) [май 1911 г.]. Распространение электрических токов в телефонных и телеграфных проводниках: курс лекций для аспирантов, прочитанных в Лондонском университете (переработанное 2-е изд.). Университетский колледж, Лондон, Великобритания: Constable & Company Ltd. ковчег:/13960/t3bz6211d . Проверено 23 июля 2023 г. (xiv+316 страниц)
• Краусс, Герберт Л. (сентябрь 1949 г.). «Схемы линий электропередачи». Электротехника . Том. 68, нет. 9. С. 766–774 [767]. дои : 10.1109/EE.1949.6444963 . eISSN   2376-7804 . ISSN   0095-9197 .
• Ли, Дональд (30 января 2013 г.). «Настройка диаграммы Смита, часть I» . Бизнес-подразделение SOC, Advantest Test Cell Innovations, Advantest Corporation . Архивировано из оригинала 9 июля 2023 г. Проверено 9 июля 2023 г. (29 страниц)
• Гамблин, Тревор (23 июля 2015 г.). «Математическая конструкция и свойства диаграммы Смита» . allaboutcircuits.com . Архивировано из оригинала 9 июля 2023 г. Проверено 9 июля 2023 г.
• Стейплс, Джон (2015). «Согласование импеданса и диаграммы Смита» (PDF) . Школа ускорителей элементарных частиц США (USPAS). Архивировано (PDF) из оригинала 9 июля 2023 г. Проверено 9 июля 2023 г. (27 страниц)

Внешние ссылки

• «Диаграмма Excel Смита» . excelhero.com . Август 2010 г. Некоммерческая интерактивная диаграмма Смита, которая лучше всего выглядит в Excel 2007+.
• «СимСмит» . ae6ty.com . Некоммерческая версия, доступна для Windows, Mac и Linux. Множество обучающих видеороликов по диаграммам Смита. Никаких ограничений по размеру схемы. Не ограничивается лестничными схемами.
• «Смит v3» . fritz.dellsperger.net . Архивировано из оригинала 4 марта 2015 г. Коммерческая и бесплатная диаграмма Смита для Windows
• «КвикСмит» . github.com/ниерадори . 2021-11-02. Бесплатный веб-образовательный инструмент «Диаграммы Смита», доступный на GitHub .
• «Инструмент 3D-диаграммы Смита» . 3dsmithchart.com . Обобщенный инструмент для создания 2D и 3D диаграмм Смита для активных и пассивных цепей (бесплатно для академических кругов и образовательных учреждений).