Роторная динамика

Роторная динамика (или динамика ротора ) — это специализированная отрасль прикладной механики, занимающаяся поведением и диагностикой вращающихся конструкций. Он обычно используется для анализа поведения различных структур — от реактивных двигателей и паровых турбин до автомобильных двигателей и компьютерных дисковых накопителей . На самом базовом уровне динамика ротора связана с одной или несколькими механическими конструкциями ( роторами ), поддерживаемыми подшипниками и находящимися под влиянием внутренних явлений, которые вращаются вокруг одной оси . Несущая конструкция называется статором . По мере увеличения скорости вращения амплитуда вибрации часто достигает максимума, называемого критической скоростью . Эта амплитуда обычно возникает из-за дисбаланса вращающейся конструкции; повседневные примеры включают балансировку двигателя и балансировку шин . Если амплитуда вибрации на этих критических скоростях чрезмерна, то катастрофический отказ происходит . Кроме того, в турбомашинах часто возникают нестабильности, связанные с внутренней конструкцией турбомашин и которые необходимо устранять. Это главная забота инженеров, проектирующих большие роторы.

Вращающееся оборудование производит вибрации в зависимости от конструкции механизма, участвующего в процессе. Любые неисправности в машине могут усилить или усилить вибрационные признаки. Вибрационное поведение машины из-за дисбаланса является одним из основных аспектов вращающихся машин, который необходимо детально изучать и учитывать при проектировании. Все объекты, включая вращающиеся механизмы, обладают собственной частотой , зависящей от структуры объекта. Критическая скорость вращающейся машины возникает, когда скорость вращения соответствует ее собственной частоте. Самая низкая скорость, при которой впервые встречается собственная частота, называется первой критической скоростью, но по мере увеличения скорости появляются дополнительные критические скорости, кратные собственной частоте. Следовательно, минимизация вращательного дисбаланса и ненужных внешних сил очень важна для уменьшения общих сил, вызывающих резонанс . Когда вибрация находится в резонансе, она создает разрушительную энергию, которая должна быть основной проблемой при проектировании вращающейся машины. Цель здесь должна состоять в том, чтобы избегать операций, близких к критическим, и безопасно проходить через них при ускорении или замедлении. Если этот аспект игнорируется, это может привести к потере оборудования, чрезмерному износу оборудования, катастрофическим поломкам, не подлежащим ремонту, или даже к травмам и человеческим жертвам.

Реальную динамику машины сложно смоделировать теоретически. Расчеты основаны на упрощенных моделях, которые напоминают различные структурные компоненты ( модели с сосредоточенными параметрами ), уравнениях, полученных в результате численного решения моделей ( метод Рэлея-Ритца ) и, наконец, на методе конечных элементов (МКЭ), который является еще одним подходом для моделирования и анализа машина для собственных частот. Существуют также некоторые аналитические методы, такие как метод распределенной передаточной функции. ^[1] который может генерировать аналитические и собственные частоты замкнутой формы, критические скорости и отклик несбалансированной массы. На любом прототипе машины он тестируется для подтверждения точных частот резонанса, а затем перепроектируется, чтобы гарантировать отсутствие резонанса.

Основные принципы

Уравнение движения в обобщенной матричной форме для осесимметричного ротора, вращающегося с постоянной скоростью вращения Ω, имеет вид

{\begin{matrix}\mathbf {M} {\ddot {\mathbf {q} }}(t)+(\mathbf {C} +\mathbf {G} ){\dot {\mathbf {q} }}(t)+(\mathbf {K} +\mathbf {N} ){\mathbf {q} }(t)&=&\mathbf {f} (t)\\\end{matrix}}

где:

M — симметричная матрица Массы.

C — симметричная матрица демпфирования

G — кососимметричная гироскопическая матрица

K — матрица жесткости симметричного подшипника или уплотнения.

N — гироскопическая матрица отклонения для включения, например, центробежных элементов.

где q — обобщенные координаты ротора в инерциальных координатах, а f — силовая функция, обычно включающая дисбаланс.

Гироскопическая матрица G пропорциональна скорости вращения Ω.Общее решение приведенного выше уравнения включает комплексные собственные векторы , которые зависят от скорости вращения.Инженерные специалисты в этой области используют диаграмму Кэмпбелла для изучения этих решений.

Интересной особенностью системы уравнений роторной динамики являются недиагональные члены жесткости, демпфирования и массы. Эти термины называются перекрестной жесткостью, перекрестным демпфированием и перекрестной массой. Когда имеется положительная поперечная жесткость, отклонение вызовет силу реакции, противоположную направлению отклонения, которая будет реагировать на нагрузку, а также силу реакции в направлении положительного вихря. Если эта сила достаточно велика по сравнению с имеющимися прямыми демпфированием и жесткостью, ротор будет неустойчивым. Когда ротор нестабильен, обычно требуется немедленная остановка машины, чтобы избежать катастрофического отказа.

Ротор Джеффкотта

Ротор Джеффкотта (названный в честь Генри Хомана Джеффкотта), также известный в Европе как ротор де Лаваля , представляет собой упрощенную модель с сосредоточенными параметрами, используемую для решения этих уравнений. Ротор Джеффкотта состоит из гибкого, невесомого, однородного вала, установленного на двух гибких подшипниках, равноудаленных от массивного диска, жестко прикрепленного к валу. Самая простая форма ротора удерживает диск в плоскости, ортогональной оси вращения. Это ограничивает реакцию ротора только на боковую вибрацию. с одной степенью свободы, Если диск идеально сбалансирован (т. е. его геометрический центр и центр масс совпадают), то ротор аналогичен незатухающему генератору находящемуся в состоянии свободной вибрации. Если между геометрическим центром и центром масс существует некоторое радиальное расстояние, то ротор неуравновешен, что создает силу, пропорциональную массе диска m , расстоянию между двумя центрами (эксцентриситету ε ) и скорости вращения диска. Ом . После расчета эквивалентной жесткости k системы мы можем создать следующее линейное обыкновенное дифференциальное уравнение второго порядка, которое описывает радиальное отклонение диска от центральной линии ротора. ^[2]

$m\mathbb {\ddot {r}} +k\mathbb {r} =m\varepsilon \Omega ^{2}sin(\Omega t)$

Если бы мы построили график радиальной реакции, мы бы увидели синусоидальную волну с угловой частотой $\Omega /2\pi$ . Это боковое колебание называется «вихрением», и в данном случае оно сильно зависит от скорости вращения. Скорость вращения не только влияет на амплитуду вынуждающей функции, но также может вызывать динамическое усиление вблизи собственной частоты системы.

Хотя ротор Джеффкотта является полезным инструментом для ознакомления с концепциями динамики ротора, важно отметить, что это математическая идеализация , которая лишь приблизительно аппроксимирует поведение реальных роторов. ^[2]

Диаграмма Кэмпбелла

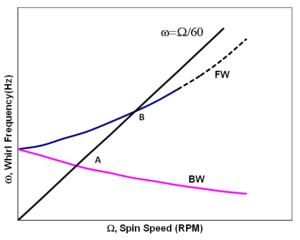
Диаграмма Кэмпбелла , также известная как «Карта вихревой скорости» или «Диаграмма частотных помех», простой роторной системы показана справа. Розовые и синие кривые показывают режимы обратного вращения (BW) и прямого вращения (FW) соответственно, которые расходятся по мере увеличения скорости вращения. Когда частота BW или частота FW равна скорости вращения Ω, на что указывают пересечения A и B с линией скорости синхронного вращения, отклик ротора может иметь пик. Это называется критической скоростью .

История

История роторной динамики полна взаимодействия теории и практики. У. Дж. М. Рэнкин впервые провел анализ вращающегося вала в 1869 году, но его модель была неадекватной, и он предсказал, что сверхкритические скорости не могут быть достигнуты. В 1895 году Данкерли опубликовал экспериментальную статью, описывающую сверхкритические скорости. Густав де Лаваль , шведский инженер, развил паровую турбину до сверхкритической скорости в 1889 году, а Керр опубликовал статью, показывающую экспериментальные доказательства второй критической скорости в 1916 году.

Лондонское королевское общество поручило Генри Джеффкотту разрешить конфликт между теорией и практикой. статью, которая сейчас считается классической, В 1919 году он опубликовал в «Философском журнале» в которой подтвердил существование стабильных сверхкритических скоростей. Август Фёппль опубликовал почти такие же выводы в 1895 году, но история в значительной степени проигнорировала его работу.

Между работой Джеффкотта и началом Второй мировой войны было проведено много работ в области нестабильностей и методов моделирования, кульминацией которых стала работа Нильса Отто Миклестада. ^[3] и М.А. Прол ^[4] что привело к появлению метода матрицы переноса (TMM) для анализа роторов. Наиболее распространенным методом, используемым сегодня для анализа динамики ротора, является метод конечных элементов .

Современные компьютерные модели были прокомментированы в цитате, приписываемой Даре Чайлдс: «качество предсказаний компьютерного кода больше связано с надежностью базовой модели и физической проницательностью аналитика … Превосходные алгоритмы или компьютер коды не помогут исправить плохие модели или недостаток инженерного мышления».

Профессор Ф. Нельсон много писал по истории роторной динамики, и большая часть этого раздела основана на его работах.

Программное обеспечение

Существует множество пакетов программного обеспечения, способных решать систему уравнений динамики ротора. Специальные коды динамики ротора более универсальны для целей проектирования. Эти коды позволяют легко добавлять коэффициенты подшипников, боковые нагрузки и многие другие параметры, которые могут понадобиться только специалисту по роторной динамике. Специальные коды, не относящиеся к роторной динамике, представляют собой полнофункциональные решатели FEA, методы решения которых разрабатывались в течение многих лет. Специальные коды, не относящиеся к динамике ротора, также можно использовать для калибровки кода, предназначенного для динамики ротора.

Специальное программное обеспечение для роторной динамики
Имя	Коммерческий / Академический	Описание
Динамика Р4 (ООО «Альфа-Транзит») ^[5]	Коммерческий	Программное обеспечение, разработанное для проектирования и анализа пространственных систем
AxSTREAM RotorDynamics, (SoftInWay) ^[6]		Интегрированная программная платформа для динамики ротора, способная определять поперечную, крутильную и осевую динамику ротора для всех широко используемых типов роторов с использованием метода конечных элементов на балочных или двумерных осесимметричных элементах и поддающаяся автоматизации.
Ротортест, (LAMAR – Университет Кампинаса ) ^[7]		Программное обеспечение на основе метода конечных элементов, включая различные типы решателей подшипников. Разработано LAMAR (Лаборатория вращающихся машин) – Unicamp (Университет Кампинас).
САМСЕФ РОТОР ^[8]		Программная платформа для моделирования роторов (LMS Samtech, подразделение Siemens)
МАДЫН (Инженеры-консультанты Клемент) ^[9]	Коммерческий	Комбинированный решатель боковых, крутильных, осевых и связанных конечных элементов для нескольких роторов и шестерен, включая фундамент и корпус.
МАДИН 2000 (DELTA JS Inc.) ^[10]	Коммерческий	Комбинированный метод конечных элементов (3D-балка Тимошенко), поперечный, крутильный, осевой и связанный решатель для нескольких роторов и шестерен, фундаментов и корпусов (возможность импорта передаточных функций и пространственных матриц состояний из других источников), различных подшипников (жидкостная пленка, пружинный демпфер, магнитный , элемент качения)
НАСТРАН (МСК/Шестиугольник)	Коммерческий	Код конечных элементов, который можно использовать для расчета диаграмм Кэмпбелла с помощью SOL 107.
iSTRDYN (ООО «ДинаТех Софтвер») ^[11]	Коммерческий	2D осесимметричный решатель методом конечных элементов
ФЕМРДИН (DynaTech Engineering, Inc.) ^[12]	Коммерческий	1-D осесимметричный решатель методом конечных элементов
DyRoBeS (Eigen Technologies, Inc.) ^[13]	Коммерческий	1D решатель элементов балки
РИМАП (РИТЕК) ^[14]	Коммерческий	1D решатель элементов балки
XLRotor (Анализ вращающегося оборудования, Inc.) ^[15]	Коммерческий	Одномерный решатель элементов балки, включая системы управления магнитными подшипниками и совмещенный анализ поперечного кручения. Мощный, быстрый и простой в использовании инструмент для динамического моделирования и анализа роторов с использованием электронных таблиц Excel. Легко автоматизируется с помощью макросов VBA, а также плагина для программного обеспечения 3D CAD.
ARMD ( Rotor Bearing Technology & Software, Inc. ) ^[16]	Коммерческий	Программное обеспечение на основе FEA для проектирования, оптимизации и оценки производительности роторной динамики, многоветвевой крутильной вибрации, пленочно-жидкостных подшипников (гидродинамических, гидростатических и гибридных), которое используется во всем мире исследователями, OEM-производителями и конечными пользователями во всех отраслях.
XLTRC2 ( Техас A&M ) ^[17]	Академический	1D решатель элементов балки
КомбоРотор ( Университет Вирджинии ) ^[18]		Комбинированный решатель поперечных, крутильных и осевых конечных элементов для нескольких роторов, оценивающих критические скорости, устойчивость и реакцию на дисбаланс, тщательно проверенный промышленным использованием.
МЕСВИР (Институт гидропроточного машиностроения Польской академии наук ) ^[19]	Академический	Пакет компьютерных программ для анализа роторно-подшипниковых систем в линейном и нелинейном диапазоне
RoDAP (Технология Д&М) ^[20]	Коммерческий	Латеральный, крутильный, осевой и связанный решатель для нескольких роторов, шестерен и гибких дисков (HDD)
РОТОРНЫЙ КОРАБЛЬ (РОТОРНЫЙ КОРАБЛЬ) ^[21]	Коммерческий	Программное обеспечение конечных элементов, разработанное французской инженерной школой (INSA-Лион) для анализа установившегося динамического поведения роторов при изгибе.
COMSOL Multiphysicals , надстройка модуля «Роторная динамика» (Модуль «Роторная динамика») ^[22]
RAPPID - (Исследование роторной динамики и уплотнений) ^[23]	Коммерческий	Библиотека программного обеспечения на основе конечных элементов (3D твердотельные и балочные элементы), включая решатели динамических коэффициентов ротора

См. также

Ссылки

Чен, В.Дж., Гюнтер, Э.Дж. (2005). Введение в динамику роторно-подшипниковых систем . Виктория, Британская Колумбия: Траффорд. ISBN 978-1-4120-5190-3 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) использует DyRoBeS
Чайлдс, Д. (1993). Явления, моделирование и анализ роторной динамики турбомашин . Уайли. ISBN 978-0-471-53840-0 .
Фредрик Ф. Эрих, изд. (1992). Справочник по роторной динамике . МакГроу-Хилл. ISBN 978-0-07-019330-7 .
Гента, Г. (2005). Динамика вращающихся систем . Спрингер. ISBN 978-0-387-20936-4 .
Джеффкотт, HH (1919). «Валы, нагруженные боковой вибрацией вблизи вихревой скорости. - Эффект отсутствия баланса». Философский журнал . 6. 37 .
Кремер, Э. (1993). Динамика роторов и фундаментов . Спрингер-Верлаг. ISBN 978-0-387-55725-0 .
Лаланн М., Феррарис Г. (1998). Прогнозирование роторной динамики в технике, второе издание . Уайли. ISBN 978-0-471-97288-4 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
Мушиньска, Агнешка (2005). Роторная динамика . ЦРК Пресс. ISBN 978-0-8247-2399-6 .
Нельсон, Ф. (июнь 2003 г.). «Краткая история ранней динамики ротора». Звук и вибрация .
Нельсон, Ф. (июль 2007 г.). «Роторная динамика без уравнений». Международный журнал COMADEM . 3. 10 . ISSN 1363-7681 .
Нельсон, Ф. (2011). Введение в роторную динамику . Том. СВМ-19 [1] . {{cite book}}: Внешняя ссылка в |volume= ( помощь )
Лаланн М., Феррарис Г. (1998). Прогнозирование роторной динамики в технике, второе издание . Уайли. ISBN 978-0-471-97288-4 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
Вэнс, Джон М. (1988). Роторная динамика турбомашин . Уайли. ISBN 978-0-471-80258-7 .
Тивари, Раджив (2017). Роторные системы: анализ и идентификация . ЦРК Пресс. ISBN 9781138036284 .
Вэнс, Джон М., Мерфи, Б., Зейдан, Ф. (2010). Вибрация машин и роторная динамика . Уайли. ISBN 978-0-471-46213-2 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
Воллан А., Комжик Л. (2012). Методы расчета динамики ротора методом конечных элементов . ЦРК Пресс. ISBN 978-1-4398-4770-1 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
Ямамото Т., Исида Ю. (2001). Линейная и нелинейная роторная динамика . Уайли. ISBN 978-0-471-18175-0 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
Ганеривала С., Мохсен Н. (2008). Роторно-динамический анализ с использованием XLRotor. SQI03-02800-0811

Примечания

^ Лю, Шибин; Ян, Бинген (22 февраля 2017 г.). «Вибрации гибких многоступенчатых роторных систем, поддерживаемых резиновыми подшипниками с водяной смазкой». Журнал вибрации и акустики . 139 (2): 021016–021016–12. дои : 10.1115/1.4035136 . ISSN 1048-9002 .
^ Перейти обратно: ^а ^б Мацусита, Осами; Танака, Масато; Канки, Хироши; Кобаяши, Масао; Кио, Патрик (2017). Вибрации вращающихся машин (1-е изд.). Япония: Спрингер. стр. 199–206. ISBN 978-4-431-55455-4 .
^ Миклестад, Нильс (апрель 1944 г.). «Новый метод расчета собственных форм несвязанных изгибных колебаний крыльев самолетов и других типов балок». Журнал авиационных наук (Институт авиационных наук) . 11 (2): 153–162. дои : 10.2514/8.11116 .
^ Прол, Массачусетс (1945), «Общий метод расчета критических скоростей гибких роторов», Trans ASME , 66 : A–142.
^ «РОТОРДИНАМИКА ТУРБОМАШИНОСТРОЕНИЯ, Программное обеспечение и инжиниринговые услуги, Компания Альфа-Транзит» . www.alfatran.com . Проверено 11 января 2022 г.
^ «AxSTREAM - Роторная динамика | Программное обеспечение для проектирования турбомашин» . www.softinway.com . 27 июля 2016 г. Проверено 11 января 2022 г.
^ "Дом" . www.fem.unicamp.br . Проверено 11 января 2022 г.
^ «Анализ динамики ротора: SAMCEF Rotors справится с этой задачей» . Архивировано из оригинала 29 сентября 2012 г. Проверено 4 июня 2013 г.
^ "Дом" . www.madyn.de . Проверено 11 января 2022 г.
^ «MADYN 2000 для роторной динамики» . www.delta-js.ch . Проверено 11 января 2022 г.
^ «Архивная копия» . Архивировано из оригинала 07 мая 2021 г. Проверено 11 января 2022 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )
^ «ФЕМРДИН» . dynatechengr.com . Проверено 11 января 2022 г.
^ «Dyrobes – революция в программном обеспечении для динамики роторов» . Проверено 11 января 2022 г.
^ «РИТЕК-РИМАП (Программный пакет для роторно-динамического анализа)» . Архивировано из оригинала 4 октября 2013 г. Проверено 1 октября 2013 г.
^ "Дом" . XLRotor . Проверено 11 января 2022 г.
^ «Динамика ротора АРМД» . Проверено 1 января 2022 г.
^ «Лаборатория турбомашин» . Turbolab.tamu.edu . Проверено 11 января 2022 г.
^ «Лаборатория вращающихся машин и средств управления» .
^ «Институт жидкостного машиностроения им. Шевальского» . Архивировано из оригинала 15 декабря 2008 г.
^ Компания «Д&М Технолоджи Лтд» . Архивировано из оригинала 06 мая 2021 г.
^ «ЛаМКоС» . lamcos.insa-lyon.fr . Проверено 11 января 2022 г.
^ «Программное обеспечение роторной динамики для прогнозного анализа вращающихся машин» . www.comsol.com . Проверено 11 января 2022 г.
^ «Исследование роторной динамики-уплотнений - РСР» . rda.гуру . Проверено 11 января 2022 г.

Внешние ссылки

[1] Лю, Шибин; Ян, Бинген (22 февраля 2017 г.). «Вибрации гибких многоступенчатых роторных систем, поддерживаемых резиновыми подшипниками с водяной смазкой». Журнал вибрации и акустики . 139 (2): 021016–021016–12. дои : 10.1115/1.4035136 . ISSN 1048-9002 .

[:0-2] Перейти обратно: ^а ^б Мацусита, Осами; Танака, Масато; Канки, Хироши; Кобаяши, Масао; Кио, Патрик (2017). Вибрации вращающихся машин (1-е изд.). Япония: Спрингер. стр. 199–206. ISBN 978-4-431-55455-4 .

[3] Миклестад, Нильс (апрель 1944 г.). «Новый метод расчета собственных форм несвязанных изгибных колебаний крыльев самолетов и других типов балок». Журнал авиационных наук (Институт авиационных наук) . 11 (2): 153–162. дои : 10.2514/8.11116 .

[4] Прол, Массачусетс (1945), «Общий метод расчета критических скоростей гибких роторов», Trans ASME , 66 : A–142.

[5] «РОТОРДИНАМИКА ТУРБОМАШИНОСТРОЕНИЯ, Программное обеспечение и инжиниринговые услуги, Компания Альфа-Транзит» . www.alfatran.com . Проверено 11 января 2022 г.

[6] «AxSTREAM - Роторная динамика | Программное обеспечение для проектирования турбомашин» . www.softinway.com . 27 июля 2016 г. Проверено 11 января 2022 г.

[7] "Дом" . www.fem.unicamp.br . Проверено 11 января 2022 г.

[8] «Анализ динамики ротора: SAMCEF Rotors справится с этой задачей» . Архивировано из оригинала 29 сентября 2012 г. Проверено 4 июня 2013 г.

[9] "Дом" . www.madyn.de . Проверено 11 января 2022 г.

[10] «MADYN 2000 для роторной динамики» . www.delta-js.ch . Проверено 11 января 2022 г.

[11] «Архивная копия» . Архивировано из оригинала 07 мая 2021 г. Проверено 11 января 2022 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )

[12] «ФЕМРДИН» . dynatechengr.com . Проверено 11 января 2022 г.

[13] «Dyrobes – революция в программном обеспечении для динамики роторов» . Проверено 11 января 2022 г.

[14] «РИТЕК-РИМАП (Программный пакет для роторно-динамического анализа)» . Архивировано из оригинала 4 октября 2013 г. Проверено 1 октября 2013 г.

[15] "Дом" . XLRotor . Проверено 11 января 2022 г.

[16] «Динамика ротора АРМД» . Проверено 1 января 2022 г.

[17] «Лаборатория турбомашин» . Turbolab.tamu.edu . Проверено 11 января 2022 г.

[18] «Лаборатория вращающихся машин и средств управления» .

[19] «Институт жидкостного машиностроения им. Шевальского» . Архивировано из оригинала 15 декабря 2008 г.

[20] Компания «Д&М Технолоджи Лтд» . Архивировано из оригинала 06 мая 2021 г.

[21] «ЛаМКоС» . lamcos.insa-lyon.fr . Проверено 11 января 2022 г.

[22] «Программное обеспечение роторной динамики для прогнозного анализа вращающихся машин» . www.comsol.com . Проверено 11 января 2022 г.

[23] «Исследование роторной динамики-уплотнений - РСР» . rda.гуру . Проверено 11 января 2022 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]