Порядковая арифметика

В математической области множеств теории порядковая арифметика описывает три обычные операции над порядковыми числами : сложение , умножение и возведение в степень . Каждый из них может быть определен двумя разными способами: либо путем создания явного хорошо упорядоченного набора , представляющего результат операции, либо с помощью трансфинитной рекурсии . Нормальная форма Кантора обеспечивает стандартизированный способ записи порядковых номеров. Помимо этих обычных порядковых операций, существуют еще «естественная» арифметика порядковых чисел и операции с числами .

Добавление

Сумма двух вполне упорядоченных наборов $S$ и $T$ представляет собой ординал, представляющий вариант лексикографического порядка с наименьшей значащей позицией в объединении декартовых произведений $S \times {0}$ и $T \times {1}$ . Таким образом, каждый элемент $S$ меньше, чем каждый элемент $T$ , сравнения внутри $S$ сохраняют тот порядок, который у них уже есть, и то же самое касается сравнений внутри $T$ .

Определение сложения $α + β$ также можно дать с помощью трансфинитной рекурсии по $β$ . Когда правое слагаемое $β = 0$ , обычное сложение дает $α + 0 = α$ для любого $α$ . Для $β > 0$ значение $α + β$ является наименьшим порядковым номером, строго большим, чем сумма $α$ и $δ$ для всех $δ < β$ . Записываем преемник и предельные порядковые номера отдельно:

$а + 0 = а$
$α + S (β) = S (α + β)$ , где $S$ обозначает функцию- преемник .
$\alpha +\beta =\bigcup _{\delta <\beta }(\alpha +\delta )$ когда $β$ является предельным порядковым номером .

Порядковое сложение натуральных чисел аналогично стандартному сложению. Первый трансфинитный ординал — это $ω$ , набор всех натуральных чисел, за которым следуют $ω + 1$ , $ω + 2$ и т. д. Порядковый номер $ω + ω$ получается из двух копий натуральных чисел, упорядоченных обычным способом, а вторая копия полностью справа от первого. Записав $0' < 1' < 2' < ...$ для второй копии, $ω + ω$ выглядит так:

0 < 1 < 2 < 3 < ... < 0' < 1' < 2' < ...

Это отличается от $ω$ , поскольку в $ω$ только $0$ не имеет прямого предшественника, тогда как в $ω + ω$ два элемента $0$ и $0'$ не имеют прямых предшественников.

Характеристики

Порядковое сложение, вообще говоря, не коммутативно . Например, $3 + ω = ω,$ поскольку отношение порядка для $3 + ω$ равно $0 < 1 < 2 < 0' < 1' < 2' < ...$ , которое можно переименовать в $ω$ . Напротив, $ω + 3$ не равно $ω,$ поскольку отношение порядка $0 < 1 < 2 < ... < 0' < 1' < 2'$ имеет наибольший элемент (а именно, $2'$ ), а $ω$ не имеет ( $ω$ и $ω +3$ равносильны , но не порядково изоморфны).

Порядковое сложение по-прежнему ассоциативно ; можно увидеть, например, что $(ω + 4) + ω = ω + (4 + ω) = ω + ω$ .

Сложение строго возрастающее и непрерывное по правому аргументу:

\alpha <\beta \Rightarrow \gamma +\alpha <\gamma +\beta

но аналогичное соотношение не выполняется для левого аргумента; вместо этого у нас есть только:

\alpha <\beta \Rightarrow \alpha +\gamma \leq \beta +\gamma

Порядковое сложение является сокращающимся слева : если $α + β = α + γ$ , то $β = γ$ . Более того, можно определить левое вычитание для ординалов $β \leq α$ : существует единственный $γ$ такой, что $α = β + γ$ . С другой стороны, отмена права не работает:

3+\omega =0+\omega =\omega

но

3\neq 0

Не действует и правое вычитание, даже если $β ⩽ α$ : например, не существует $γ$ такого, что $γ + 42 = ω$ .

Если ординалы меньше $α$ замкнуты при сложении и содержат 0, то $α$ иногда называют $γ$ -числом (см. аддитивно неразложимый ординал ). Это в точности ординалы вида $ω б$ .

Умножение

Непересекающийся союз

html.skin-theme-clientpref-night .mw-parser-output div:not(.notheme)>.tmp-color,html.skin-theme-clientpref-night .mw-parser-output p>.tmp-color,html.skin-theme-clientpref-night .mw-parser-output table:not(.notheme) .tmp-color{color:inherit!important}@media(prefers-color-scheme:dark){html.skin-theme-clientpref-os .mw-parser-output div:not(.notheme)>.tmp-color,html.skin-theme-clientpref-os .mw-parser-output p>.tmp-color,html.skin-theme-clientpref-os .mw-parser-output table:not(.notheme) .tmp-color{color:inherit!important}} { (n,0) : n \in N} \cup { (n,1) : n \in N}

, использующий лексикографический порядок с наименьшей значимой позицией первой, имеет тип порядка

ω • 2

. Это отличается от

ω

.

Набор

{(0, п), (1, n) : n \in N}

в лексикографическом порядке с наименьшей значащей позицией первой имеет тип порядка

2 • ω

, который равен

ω

.

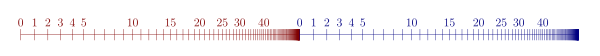
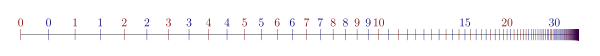
S Декартово произведение двух $\times T лексикографического$ вполне упорядоченных наборов $S$ и $T$ может быть упорядочено с помощью варианта порядка , в котором наименее значимая позиция ставится на первое место. сути, каждый элемент $T$ заменяется несвязной копией $S.$ По Тип порядка декартова произведения — это порядковый номер, который получается в результате умножения типов порядка $S$ и $T$ .

Определение умножения также можно дать с помощью трансфинитной рекурсии на $β$ . Когда правый множитель $β = 0$ , обычное умножение дает $α \cdot 0 = 0$ для любого $α$ . Для $β > 0$ значение $α \cdot β$ — это наименьший порядковый номер, больший или равный $(α \cdot δ) + α$ для всех $δ < β$ . Записываем преемник и предельные порядковые номера отдельно:

$а$ · 0 = 0.
$α \cdot S (β) знак равно (α \cdot β) + α$ , для порядкового номера преемника $S (β)$ .
$\alpha \cdot \beta =\bigcup _{\delta <\beta }(\alpha \cdot \delta )$ , когда $β$ является предельным порядковым номером.

В качестве примера приведем отношение порядка для $ω \cdot 2$ :

0 ₀ < 1 ₀ < 2 ₀ < 3 ₀ < ... < 0 ₁ < 1 ₁ < 2 ₁ < 3 ₁ < ...,

который имеет тот же тип порядка, что и $ω + ω$ . Напротив, $2 \cdot ω$ выглядит так:

0 ₀ < 1 ₀ < 0 ₁ < 1 ₁ < 0 ₂ < 1 ₂ < 0 ₃ < 1 ₃ < ...

и после перемаркировки это выглядит так же, как $ω$ .Таким образом, $ω \cdot 2 = ω + ω \neq ω = 2 \cdot ω$ , показывая, что умножение ординалов, вообще говоря, не является коммутативным, см. изображения.

Как и в случае сложения, порядковое умножение натуральных чисел аналогично стандартному умножению.

Характеристики

$α \cdot 0 = 0 \cdot α = 0$ , и имеет место свойство нулевого произведения : $α \cdot β = 0 \to α = 0$ или $β = 0$ . Порядковый номер 1 является мультипликативным тождеством, $α \cdot 1 = 1 \cdot α = α$ . Умножение ассоциативно, $(α \cdot β) \cdot γ = α \cdot (β \cdot γ)$ . Умножение строго возрастающее и непрерывное по правому аргументу: ( $α < β$ и $γ > 0$ ) → $γ \cdot α < γ \cdot β$ . Умножение не является строго возрастающим по левому аргументу, например, 1 < 2, а $1 \cdot ω = 2 \cdot ω = ω$ . Однако оно (нестрого) возрастает, т. е. $α \leq β$ → $α \cdot γ \leq β \cdot γ$ .

Умножение порядковых чисел, вообще говоря, не является коммутативным. В частности, натуральное число больше 1 никогда не коммутирует ни с каким бесконечным ординалом, а два бесконечных ординала $α$ и $β$ коммутируют тогда и только тогда, когда $α м = б н$ для некоторых ненулевых натуральных чисел $m$ и $n$ . Отношение « $α$ коммутирует с $β$ » является отношением эквивалентности для порядковых номеров больше 1, и все классы эквивалентности счетно бесконечны.

дистрибутивность Слева имеет место $: α (β + γ) = αβ + αγ$ . Однако закон распределения справа $(β + γ) α = βα + γα$ в общем случае не верен : $(1 + 1) \cdot ω = 2 \cdot ω = ω,$ в то время как $1 \cdot ω + 1 \cdot ω = ω + ω$ , что отличается. Существует закон левого сокращения : если $α > 0$ и $α \cdot β = α \cdot γ$ , то $β = γ$ . Правое сокращение не работает, например $1 \cdot ω = 2 \cdot ω = ω$ , но 1 и 2 разные. со Имеет место левое деление свойством α остатка: для всех $и$ β $,$ если $β > 0$ , то существуют единственные $γ$ и $δ$ такие, что $α = β \cdot γ + δ$ и $δ < β$ . Правое деление не работает: не существует $α$ такого, что $α \cdot ω \leq ω ой \leq (α + 1) \cdot ω$ .

Порядковые номера образуют левое почти полукольцо , но не образуют кольца . Следовательно, ординалы не являются евклидовой областью , поскольку они даже не являются кольцом; более того, евклидова «норма» будет иметь порядковый номер с использованием здесь левого деления.

δ $αβ$ -число (см. Мультипликативно неразложимый ординал ) — это ординал $β,$ больший 1, такой, что $= β всякий$ раз, когда $0 < α < β$ . Они состоят из ординала 2 и ординалов вида $β = ω ой с$ .

Возведение в степень

Определение возведения в степень с помощью типов порядка легче всего объяснить, используя определение фон Неймана порядкового числа как набора всех меньших порядковых номеров . Тогда для построения множества порядка типа $α б$ рассмотрим множество всех функций $f : β \to α$ таких, что $f (x) = 0$ для всех, кроме конечного числа элементов $x \in β$ (по сути, мы рассматриваем функции с конечным носителем ). Этот набор упорядочен лексикографически, начиная с наименее значимой позиции: мы пишем $f < g$ тогда и только тогда, когда существует $x \in β$ с $f (x) < g (x)$ и $f (y) = g (y)$ для всех $y \in . β$ с $x < y$ . Это хороший порядок и, следовательно, дает порядковый номер.

Определение возведения в степень также можно дать с помощью трансфинитной рекурсии по показателю $β$ . Когда показатель степени $β = 0$ , обычное возведение в степень дает $α 0 = 1$ для любого $α$ . При $β > 0$ значение $α б$ - наименьший порядковый номер, больший или равный $α д \cdot α$ для всех $δ < β$ . Записываем преемник и предельные порядковые номера отдельно:

$а 0 = 1$ .
$а С (б) = (а б) \cdot α$ , для порядкового номера преемника $S (β)$ .
$\alpha ^{\beta }=\bigcup _{0<\delta <\beta }(\alpha ^{\delta })$ , когда $β$ является предельным порядковым номером.

Оба определения значительно упрощаются, если показатель степени $β$ является конечным числом: $α б$ тогда это просто произведение $β$ копий $α$ ; например $ω 3 = ω \cdot ω \cdot ω$ , а элементы $ω 3$ можно рассматривать как тройки натуральных чисел, упорядоченные лексикографически, начиная с наименее значимой позиции. Это согласуется с обычным возведением в степень натуральных чисел.

Но для бесконечных показателей определение может быть неочевидным. Например, $α ой$ можно отождествить с множеством конечных последовательностей элементов $α$ , правильно упорядоченных. Уравнение $2 ой = ω$ выражает тот факт, что конечные последовательности нулей и единиц можно отождествлять с натуральными числами, используя двоичную систему счисления . Порядковый номер $ω ой$ можно рассматривать как тип порядка конечных последовательностей натуральных чисел; каждый элемент $ω ой$ (т.е. каждый ординал, меньший, чем $ω ой$ ) можно однозначно записать в виде $\omega ^{n_{1}}c_{1}+\omega ^{n_{2}}c_{2}+\cdots +\omega ^{n_{k}}c_{k}$ где $k$ , $n 1$ , ..., $nk —$ натуральные числа, $1,$ ..., $c k$ — ненулевые натуральные числа и $n 1 > ... > nk c$ .

То же самое верно и в целом: каждый элемент $α б$ (т.е. каждый порядковый номер, меньший, чем $α б$ ) можно однозначно записать в виде $\alpha ^{b_{1}}a_{1}+\alpha ^{b_{2}}a_{2}+\cdots +\alpha ^{b_{k}}a_{k}$ где $k$ - натуральное число, $b 1$ , ..., $b k$ - порядковые номера, меньшие, чем $β$ , при этом $b 1 > ... > b k$ , а $a 1, ..., a k$ - ненулевые ординалы, меньшие, чем $α$ . Это выражение соответствует функции $f : β \to α$ , которая переводит $b i$ в $a i$ для $i = 1, ..., k$ и переводит все остальные элементы $β$ в 0.

возведения в степень используется одна и та же нотация экспоненты Хотя для порядкового и кардинального , эти две операции совершенно разные, и их не следует путать. Кардинальное возведение в степень $A Б$ определяется как кардинальное число множества всех функций $B \to A$ , а порядковое возведение в степень $α б$ содержит только функции $β \to α$ с конечным носителем, обычно набор гораздо меньшей мощности. Чтобы не путать порядковое возведение в степень с кардинальным возведением в степень, можно использовать символы для порядковых номеров (например, $ω$ ) в первом и символы для кардинальных чисел (например, $\aleph _{0}$ ) в последнем.

Характеристики

$а 0 = 1$ .
Если $0 < α$ , то $0 а = 0$ .
$1 а = 1$ .
$а 1 = а$ .
$а б \cdot а с = а б + в$ .
$(а б) с = а б в$ .
Существуют $α$ , $β$ и $γ,$ для которых $(α \cdot β) с \neq а с \cdot б с$ . Например, $(ω \cdot 2) 2 = ω \cdot2\cdot ω \cdot2 = ω 2 \cdot 2 \neq ω 2 \cdot 4$ .
Порядковое возведение в степень строго возрастает и непрерывно по правому аргументу: если $γ > 1$ и $α < β$ , то $γ а < γ б$ .
Если $α < β$ , то $α с \leq б с$ . Обратите внимание, например, что 2 < 3 и все же $2 ой = 3 ой = о$ .
Если $α > 1$ и $α б = а с$ , то $β = γ$ . Если $α = 1$ или $α = 0,$ это не так.
Для всех $α$ и $β$ , если $β > 1$ и $α > 0,$ то существуют единственные $γ$ , $δ$ и $ρ$ такие, что $α = β с \cdot δ + ρ$ такие, что $0 < δ < β$ и $ρ < β с$ .

Якобсталь показал, что единственные решения уравнения $α б = б а$ с $α \leq β$ задаются формулами $α = β$ , или $α = 2$ и $β = 4$ , или $α$ — любой предельный порядковый номер и $β = εα$ , где $ε$ — $ε$ -число, большее, чем $α$ . ^[1]

За пределами возведения в степень

Существуют порядковые операции, которые продолжают последовательность, начатую сложением, умножением и возведением в степень, включая порядковые версии тетрации , пентации и гексации . См. также функцию Веблена .

Канторова нормальная форма

Каждое порядковое число $α$ можно однозначно записать как $\omega ^{\beta _{1}}c_{1}+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}$ , где $k$ — натуральное число, $c_{1},c_{2},\ldots ,c_{k}$ являются ненулевыми натуральными числами, а $\beta _{1}>\beta _{2}>\ldots >\beta _{k}\geq 0$ являются порядковыми числами. Вырожденный случай $α = 0$ имеет место, когда $k = 0$ и нет $β$ s и $c$ s. разложение $α$ называется канторовой нормальной формой α $Это$ и может рассматриваться как $по основанию ω$ позиционная система счисления . Самый высокий показатель $\beta _{1}$ называется степенью $\alpha$ , и удовлетворяет $\beta _{1}\leq \alpha$ . Равенство $\beta _{1}=\alpha$ применимо тогда и только тогда, когда $\alpha =\omega ^{\alpha }$ . В этом случае нормальная форма Кантора не выражает порядковый номер через меньшие; это может произойти, как описано ниже.

Небольшая вариация нормальной формы Кантора, с которой обычно немного проще работать, состоит в том, чтобы установить все числа $c i$ равными 1 и позволить показателям быть равными. Другими словами, каждый порядковый номер α можно однозначно записать как $\omega ^{\beta _{1}}+\omega ^{\beta _{2}}+\cdots +\omega ^{\beta _{k}}$ , где $k$ — натуральное число, а $\beta _{1}\geq \beta _{2}\geq \ldots \geq \beta _{k}\geq 0$ являются порядковыми числами.

Другой вариант нормальной формы Кантора - это «разложение по базе $δ$ », где $ω$ заменяется любым порядковым номером $δ > 1$ , а числа $c i$ являются ненулевыми порядковыми числами, меньшими, чем $δ$ .

Нормальная форма Кантора позволяет нам однозначно выражать и упорядочивать ординалы $α$ , построенные из натуральных чисел с помощью конечного числа арифметических операций сложения, умножения и возведения в степень. $\omega$ : другими словами, предполагая $\beta _{1}<\alpha$ в нормальной форме Кантора мы также можем выразить показатели степени $\beta _{i}$ в нормальной форме Кантора и сделав то же предположение для $\beta _{i}$ что касается $α$ и так далее рекурсивно, то получим систему обозначений этих ординалов (например,

\omega ^{\omega ^{\omega ^{7}\cdot 6+\omega +42}\cdot 1729+\omega ^{9}+88}\cdot 3+\omega ^{\omega ^{\omega }}\cdot 5+65537

обозначает порядковый номер).

Порядковый номер ε ₀ ( эпсилон ноль ) представляет собой набор порядковых значений α арифметических выражений конечной длины канторовой нормальной формы, которые наследственно нетривиальны, где нетривиальность означает β ₁ < α , когда 0 < α . Это наименьший порядковый номер, который не имеет конечного арифметического выражения через $ω$ , и наименьший порядковый номер такой, что $\varepsilon _{0}=\omega ^{\varepsilon _{0}}$ , т.е. в нормальной канторовской форме показатель степени не меньше самого ординала. Это предел последовательности

0,\,1=\omega ^{0},\,\omega =\omega ^{1},\,\omega ^{\omega },\,\omega ^{\omega ^{\omega }},\,\ldots \,.

Порядковый номер ε ₀ важен по разным причинам в арифметике (в основном потому, что он измеряет теоретико -доказательную силу первого порядка арифметики Пеано : то есть аксиомы Пеано могут демонстрировать трансфинитную индукцию до любого порядкового номера меньше ε ₀ , но не до само ε ₀ ).

Нормальная форма Кантора также позволяет нам вычислять суммы и произведения ординалов: например, для вычисления суммы нужно просто знать (см. свойства, перечисленные в § Сложение и § Умножение ), что

\omega ^{\beta }c+\omega ^{\beta '}c'=\omega ^{\beta '}c'\,,

если $\beta '>\beta$ (если $\beta '=\beta$ можно применить распределительный закон слева и переписать это как $\omega ^{\beta }(c+c')$ , и если $\beta '<\beta$ выражение уже находится в нормальной форме Кантора); и для вычисления продуктов существенные факты заключаются в том, что когда $0<\alpha =\omega ^{\beta _{1}}c_{1}+\cdots +\omega ^{\beta _{k}}c_{k}$ находится в нормальной канторовской форме и $0<\beta '$ , затем

\alpha \omega ^{\beta '}=\omega ^{\beta _{1}+\beta '}\,

и

\alpha n=\omega ^{\beta _{1}}c_{1}n+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}\,,

если $n$ — ненулевое натуральное число.

Чтобы сравнить два ординала, записанных в нормальной форме Кантора, сначала сравните $\beta _{1}$ , затем $c_{1}$ , затем $\beta _{2}$ , затем $c_{2}$ , и так далее. При первом появлении неравенства порядковый номер, имеющий больший компонент, является большим порядковым номером. Если они одинаковы, пока один из них не завершится раньше другого, то тот, который завершится первым, будет меньше.

Факторизация в простые числа

Эрнст Якобсталь показал, что ординалы удовлетворяют определенной форме теоремы о факторизации: каждый ненулевой ординал можно записать как произведение конечного числа простых ординалов. Эта факторизация на простые порядковые числа, как правило, не уникальна, но существует «минимальная» факторизация на простые числа, которая уникальна с точностью до изменения порядка конечных простых множителей ( Серпинский 1958 ).

Простой порядковый номер — это порядковый номер больше 1, который нельзя записать в виде произведения двух меньших порядковых номеров. Некоторые из первых простых чисел: 2, 3, 5, ..., $ω$ , $ω + 1$ , $ω. 2 +1$ , $ох 3 + 1$ , ..., $о ой$ , $ой ой +1$ , $ох о + 1 + 1$ , ... Существует три вида простых ординалов:

Конечные простые числа 2, 3, 5,...
Ординалы вида $ω ой а$ для любого порядкового номера $α$ . Это простые ординалы, которые являются пределами, и дельта-числа , трансфинитные ординалы, замкнутые при умножении.
Ординалы вида $ω а + 1$ для любого порядкового номера $α > 0$ . Это бесконечные простые числа-преемники и последователи гамма-числ , аддитивно неразложимых ординалов.

Факторизация на простые числа не является однозначной: например, $2\times3 = 3\times2$ , $2\times ω = ω$ , $(ω +1)\times ω = ω \times ω$ и $ω \times ω. ой = о ой$ . Однако существует уникальная факторизация на простые числа, удовлетворяющая следующим дополнительным условиям:

Каждое предельное простое число должно встречаться перед любым последующим простым числом.
Если два последовательных простых числа простой факторизации оба являются пределами или оба конечны, второе должно быть меньше или равно первому.

Эту простую факторизацию можно легко прочитать, используя нормальную форму Кантора, следующим образом:

Сначала запишите порядковый номер как произведение $αβ$ , где $α$ — наименьшая степень $ω$ в нормальной форме Кантора, а $β$ — его преемник.
Если $α = ω с$ тогда запись $γ$ в нормальной канторовской форме дает разложение $α$ как произведение предельных простых чисел.
Теперь посмотрим на нормальную форму Кантора $β$ . Если $β = ω л м + ω м n$ + меньшие члены, то $β = (ω м n + меньшие члены)(ω л - м + 1) m$ — произведение меньшего порядкового номера, простого и натурального числа $m$ . Повторение этого и разложение натуральных чисел на простые числа дает факторизацию простых чисел $β$ .

Таким образом, факторизация порядкового ординала нормальной формы Кантора

ой 1 ​ п 1 + \dots + ω α к n k

(при

α 1 > \dots > α k

)

в минимальное произведение бесконечных простых и натуральных чисел есть

(ой ой б 1 \dots ох ой β м) n k (ω α k -1 -α k + 1) n k -1 \dots (ω α 1 - α 2 + 1) н 1

где каждое $n i$ должно быть заменено его факторизацией в невозрастающую последовательность конечных простых чисел и

α k = ω б 1 + \dots + ох β м

с

β 1 \geq \dots \geq β м

.

Большие счетные ординалы

Как обсуждалось выше, нормальная форма Кантора ординалов ниже ε ₀ может быть выражена в алфавите, содержащем только функциональные символы для сложения, умножения и возведения в степень, а также постоянные символы для каждого натурального числа и для $ω$ . Мы можем избавиться от бесконечного числа цифр, используя только постоянный символ 0 и операцию-преемник S (например, натуральное число 4 можно выразить как S(S(S(S(0))))). Это описывает порядковую запись : систему обозначения порядковых номеров в конечном алфавите. Эта конкретная система порядковых обозначений называется совокупностью арифметических порядковых выражений и может выражать все порядковые номера ниже ε ₀ , но не может выражать ε ₀ . Существуют и другие порядковые обозначения, способные фиксировать порядковые номера далеко за пределами ε ₀ , но поскольку в любом конечном алфавите существует только счетное количество строк конечной длины, для любой заданной порядковой записи будут порядковые номера ниже $ω 1$ ( первый несчетный порядковый номер ), которые невыразимо. Такие ординалы называются большие счетные ординалы .

Операции сложения, умножения и возведения в степень являются примерами примитивно-рекурсивных порядковых функций , а более общие примитивно-рекурсивные порядковые функции могут использоваться для описания более крупных порядковых чисел.

Естественные операции

Операции натуральной суммы и натурального произведения над ординалами были определены в 1906 году Герхардом Хессенбергом и иногда называются суммой (или произведением) Хессенберга ( Серпинский 1958 ). Натуральная сумма $α$ и $β$ часто обозначается $α \oplus β$ или $α # β$ , а натуральное произведение — $α \otimes β$ или $α ⨳ β$ .

Натуральная сумма и произведение определяются следующим образом. Позволять $\alpha =\omega ^{\alpha _{1}}+\cdots +\omega ^{\alpha _{k}}$ и $\beta =\omega ^{\beta _{1}}+\cdots +\omega ^{\beta _{\ell }}$ находиться в нормальной канторовской форме (т.е. $\alpha _{1}\geq \cdots \geq \alpha _{k}$ и $\beta _{1}\geq \cdots \geq \beta _{\ell }$ ). Позволять $\gamma _{1},\ldots ,\gamma _{k+\ell }$ быть представителями $\alpha _{1},\ldots ,\alpha _{k},\beta _{1},\ldots ,\beta _{\ell }$ отсортированы в невозрастающем порядке. Затем $\alpha \oplus \beta$ определяется как $\alpha \oplus \beta =\omega ^{\gamma _{1}}+\cdots +\omega ^{\gamma _{k+\ell }}.$ Натуральный продукт $\alpha$ и $\beta$ определяется как $\alpha \otimes \beta =\bigoplus _{\begin{aligned}&1\leq i\leq k\\&1\leq j\leq \ell \end{aligned}}\omega ^{\alpha _{i}\oplus \beta _{j}}.$ Например, предположим $\alpha =\omega ^{\omega ^{\omega }}+\omega$ и $\beta =\omega ^{\omega }+\omega ^{5}$ . Затем $\alpha \oplus \beta =\omega ^{\omega ^{\omega }}+\omega ^{\omega }+\omega ^{5}+\omega$ , тогда как $\alpha +\beta =\omega ^{\omega ^{\omega }}+\omega ^{\omega }+\omega ^{5}$ . И $\alpha \otimes \beta =\omega ^{\omega ^{\omega }+\omega }+\omega ^{\omega ^{\omega }+5}+\omega ^{\omega +1}+\omega ^{6}$ , тогда как $\alpha \beta =\omega ^{\omega ^{\omega }+\omega }+\omega ^{\omega ^{\omega }+5}$ .

Натуральная сумма и произведение коммутативны и ассоциативны, а натуральный продукт распределяется по натуральной сумме. Операции также монотонны в том смысле, что если $\alpha <\beta$ затем $\alpha \oplus \gamma <\beta \oplus \gamma$ ; если $\alpha \leq \beta$ затем $\alpha \otimes \gamma \leq \beta \otimes \gamma$ ; и если $\alpha <\beta$ и $\gamma >0$ затем $\alpha \otimes \gamma <\beta \otimes \gamma$ .

У нас есть $\underbrace {\alpha \oplus \cdots \oplus \alpha } _{n}=\alpha \otimes n$ .

У нас всегда есть $\alpha +\beta \leq \alpha \oplus \beta$ и $\alpha \beta \leq \alpha \otimes \beta$ . Если оба $\alpha <\omega ^{\gamma }$ и $\beta <\omega ^{\gamma }$ затем $\alpha \oplus \beta <\omega ^{\gamma }$ . Если оба $\alpha <\omega ^{\omega ^{\gamma }}$ и $\beta <\omega ^{\omega ^{\gamma }}$ затем $\alpha \otimes \beta <\omega ^{\omega ^{\gamma }}$ .

Натуральная сумма и произведение не непрерывны по правильному аргументу, так как, например, $\lim _{n<\omega }\alpha \oplus n=\alpha +\omega$ , и не $\alpha \oplus \omega$ ; и $\lim _{n<\omega }\alpha \otimes n=\alpha \omega$ , и не $\alpha \otimes \omega$ .

Натуральная сумма и произведение — это то же самое, что сложение и умножение (ограниченное порядковыми числами) Джона Конвея поля сюрреалистических чисел .

Естественные операции возникают в теории вполне частичных порядков ; учитывая два хорошо частичных заказа $S$ и $T$ , типов (максимальные линеаризации ) $o(S)$ и $o(T)$ , тип непересекающегося объединения $o(S)\oplus o(T)$ , а тип прямого произведения $o(S)\otimes o(T)$ . ^[2] Можно принять это соотношение как определение естественных операций, выбрав $S$ и $T$ в качестве ординалов $α$ и $β$ ; поэтому $α \oplus β$ — тип максимального порядка полного порядка, расширяющего несвязное объединение (как частичный порядок) $α$ и $β$ ; а $α \otimes β$ — тип максимального порядка полного порядка, расширяющего прямое произведение (как частичный порядок) $α$ и $β$ . ^[3] Полезное применение этого - когда $α$ и $β$ оба являются подмножествами некоторого большего общего порядка; то их объединение имеет тип порядка не выше $α \oplus β$ . Если они оба являются подмножествами некоторой упорядоченной абелевой группы , то их сумма имеет тип порядка не выше $α \otimes β$ .

Мы также можем определить натуральную сумму $α \oplus β$ путем одновременной трансфинитной рекурсии по $α$ и $β$ как наименьший ординал, строго больший, чем натуральная сумма $α$ и $γ$ для всех $γ < β$ и $γ$ и $β$ для всех $γ < α$ . Аналогично, мы можем определить натуральный продукт $α \otimes β$ путем одновременной трансфинитной рекурсии по $α$ и $β$ как наименьший ординал, который одновременно больше или равен $(γ \otimes β) \oplus β$ для всех $γ < α$ и больше или равен $(α \otimes γ) \oplus α$ для всех $γ < β$ . Также см. статью о сюрреалистических числах , чтобы узнать определение натурального умножения в этом контексте; однако он использует сюрреалистическое вычитание, которое не определено для порядковых номеров.

Натуральная сумма ассоциативна и коммутативна. Она всегда больше или равна обычной сумме, но может быть и строго больше. Например, натуральная сумма $ω$ и 1 равна $ω + 1$ (обычная сумма), но это также натуральная сумма 1 и $ω$ . Натуральный продукт ассоциативен и коммутативен и распределяется по натуральной сумме. Натуральный продукт всегда больше или равен обычному продукту, но может быть строго больше. Например, натуральный продукт $ω$ и 2 — это $ω \cdot 2$ (обычный продукт), но это также натуральный продукт 2 и $ω$ .

При естественном сложении ординалы можно отождествить с элементами свободного коммутативного моноида, порожденного гамма-числами $ω а$ . При естественном сложении и умножении ординалы можно отождествить с элементами свободного коммутативного полукольца, порожденного дельта-числами $ω ой а$ .Порядковые числа не имеют уникальной разложения на простые числа под натуральным произведением. Хотя полное кольцо многочленов имеет уникальную факторизацию, подмножество многочленов с неотрицательными коэффициентами ее не имеет: например, если $x$ — любое дельта-число, то

х 5 + х 4 + х 3 + х 2 + х + 1 = (х + 1) (х 4 + х 2 + 1) = (х 2 + х + 1) (х 3 + 1)

имеет два несовместимых выражения как натуральный продукт многочленов с неотрицательными коэффициентами, которые невозможно разложить дальше.

Нимберская арифметика

Существуют арифметические операции над порядковыми числами в силу взаимно однозначного соответствия между порядковыми числами и числами . Тремя распространенными операциями над числами являются сложение чисел, умножение чисел и минимальное исключение (mex) . Сложение числителей — это обобщение побитового исключающего действия или операции над натуральными числами. Mex $отсутствующий$ набора порядковых номеров — это наименьший порядковый номер, в наборе.

Примечания

^ Эрнст Якобсталь, Взаимозаменяемость трансфинитных порядковых чисел, Mathematical Annals , Vol 64 (1907), 475-488. Доступно здесь
^ DHJ Де Йонг и Р. Парих, Частичные порядки и иерархии, Indag. Математика. 39 (1977), 195–206. Доступно здесь
^ Филип В. Каррут, Арифметика ординалов с приложениями к теории упорядоченных абелевых групп, Bull. амер. Математика. Соц. 48 (1942), 262–271. См. теорему 1. Доступно здесь.

Ссылки

Томас Джех (21 марта 2006 г.). Теория множеств: издание третьего тысячелетия, переработанное и дополненное . Springer Science & Business Media. ISBN 978-3-540-44085-7 .
Кунен, Кеннет , 1980. Теория множеств: введение в доказательства независимости . Эльзевир. ISBN 0-444-86839-9 .
Серпинский, Вацлав (1958), Кардинальные и порядковые числа , Monografie Matematyczne Польской академии наук, том 34, Варшава: Państwowe Wydawnictwo Naukowe, MR 0095787

Внешние ссылки

ordCalc порядковый калькулятор

[1] Эрнст Якобсталь, Взаимозаменяемость трансфинитных порядковых чисел, Mathematical Annals , Vol 64 (1907), 475-488. Доступно здесь

[2] DHJ Де Йонг и Р. Парих, Частичные порядки и иерархии, Indag. Математика. 39 (1977), 195–206. Доступно здесь

[3] Филип В. Каррут, Арифметика ординалов с приложениями к теории упорядоченных абелевых групп, Bull. амер. Математика. Соц. 48 (1942), 262–271. См. теорему 1. Доступно здесь.

[1]

[2]

[3]