Динамическое рассеяние света

Гипотетическое динамическое светорассеяние двух образцов: более крупные частицы вверху и более мелкие частицы внизу.

Динамическое рассеяние света ( ДРС ) – это метод в физике , который можно использовать для определения профиля распределения по размерам мелких частиц в суспензии или полимеров в растворе . ^[1] В рамках DLS временные флуктуации обычно анализируются с использованием интенсивности или фотонной автокорреляционной функции (также известной как фотонная корреляционная спектроскопия – PCS или квазиупругое рассеяние света – QELS ). При анализе во временной области автокорреляционная функция (АКФ) обычно затухает, начиная с нулевого времени задержки, а более быстрая динамика из-за меньших частиц приводит к более быстрой декорреляции следа рассеянной интенсивности. Показано, что АКФ интенсивности представляет собой Фурье-преобразование спектра мощности , и поэтому измерения ДЛС могут быть одинаково хорошо выполнены в спектральной области. ^[2]^[3] DLS также можно использовать для исследования поведения сложных жидкостей, таких как концентрированные растворы полимеров.

Настраивать

Монохроматический источник света, обычно лазер, пропускается через поляризатор в образец. Рассеянный свет затем проходит через второй поляризатор, где он собирается фотоумножителем, и полученное изображение проецируется на экран. Это известно как спекл-паттерн (рис. 1). ^[4]

На все молекулы раствора воздействует свет, и все молекулы преломляют свет во всех направлениях. Дифрагированный свет от всех молекул может интерферировать либо конструктивно (светлые области), либо разрушительно (темные области). Этот процесс повторяется через короткие промежутки времени, и полученный набор спекл-паттернов анализируется автокоррелятором, который сравнивает интенсивность света в каждой точке с течением времени. Поляризаторы могут быть установлены в двух геометрических конфигурациях. Одна из них — это вертикальная/вертикальная (VV) геометрия, при которой второй поляризатор пропускает свет в том же направлении, что и основной поляризатор. В вертикально-горизонтальной (VH) геометрии второй поляризатор пропускает свет, направленный не в том же направлении, что и падающий свет.

Описание

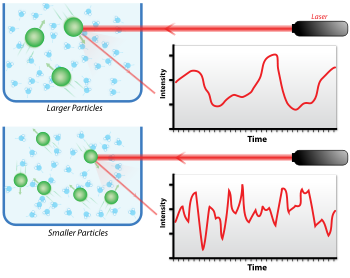
Когда свет попадает на мелкие частицы, свет рассеивается во всех направлениях ( рэлеевское рассеяние ), пока частицы малы по сравнению с длиной волны (ниже 250 нм ). Даже если источником света является лазер и, следовательно, он монохроматический и когерентный , интенсивность рассеяния колеблется со временем. Это колебание происходит из-за того, что мелкие частицы в суспензии испытывают броуновское движение , поэтому расстояние между рассеивателями в растворе постоянно меняется со временем. Затем этот рассеянный свет подвергается либо конструктивному, либо деструктивному вмешательству со стороны окружающих частиц, и внутри этого колебания интенсивности содержится информация о временном масштабе движения рассеивателей. Подготовка проб путем фильтрации или центрифугирования имеет решающее значение для удаления пыли и артефактов из раствора.

Динамическая информация о частицах получается из автокорреляции следа интенсивности, записанного во время эксперимента. Кривая автокорреляции второго порядка генерируется на основе трассы интенсивности следующим образом:

g^{2}(q;\tau )={\frac {\langle I(t)I(t+\tau )\rangle }{\langle I(t)\rangle ^{2}}}

где $г 2 (q; τ)$ — автокорреляционная функция для конкретного волнового вектора $q$ и времени задержки $τ$ , а $I$ — интенсивность. Угловые кронштейны $\langle \cdot \rangle$ обозначают оператор ожидаемого значения , который в некоторых текстах обозначается заглавной $E.$ буквой

При коротких временных задержках корреляция высока, поскольку у частиц нет возможности в значительной степени переместиться из исходного состояния, в котором они находились. Таким образом, два сигнала практически не изменяются при сравнении после очень короткого интервала времени. По мере увеличения временных задержек корреляция затухает экспоненциально, а это означает, что по прошествии длительного периода корреляция между интенсивностью рассеяния начального и конечного состояний отсутствует. Этот экспоненциальный затух связан с движением частиц, в частности с коэффициентом диффузии. Для подбора затухания (т.е. автокорреляционной функции) используются численные методы, основанные на расчетах предполагаемых распределений. Если образец монодисперсный (однородный), то затухание представляет собой просто одну экспоненциальную зависимость. Уравнение Зигерта связывает автокорреляционную функцию второго порядка с автокорреляционной функцией первого порядка $g 1 (q; τ)$ следующим образом:

g^{2}(q;\tau )=1+\beta \left[g^{1}(q;\tau )\right]^{2}

где первый член суммы связан с базовым значением (≈1), а параметр $β$ представляет собой поправочный коэффициент, который зависит от геометрии и ориентации лазерного луча в установке светорассеяния. Оно примерно равно обратному числу спеклов (см. Паттерн спеклов ), из которых собирается свет. Меньший фокус лазерного луча дает более грубую картину спеклов, меньшее количество спеклов на детекторе и, следовательно, большую автокорреляцию второго порядка. Наиболее важным применением функции автокорреляции является ее использование для определения размера.

Многократное рассеяние

Динамическое рассеяние света дает представление о динамических свойствах мягких материалов путем измерения единичных событий рассеяния. Это означает, что каждый обнаруженный фотон рассеивался образцом ровно один раз. В принципе, измерения ДЛС можно проводить, установив детектор под любым углом. Выбор наилучшего угла зависит от свойств образца, таких как мутность и размер частиц. ^[5] Обнаружение обратного рассеяния (например, 173° или 175°) особенно интересно для мутных и высококонцентрированных образцов, содержащих крупные частицы. Обнаружение бокового рассеяния (90°) рекомендуется для слабо рассеивающих образцов, включая мелкие частицы и прозрачные образцы. Наконец, обнаружение прямого рассеяния (например, 13° или 15°) подходит для обнаружения образцов, содержащих мелкие частицы с небольшим количеством крупных частиц. Некоторые инструменты DLS, представленные на рынке, также позволяют автоматически выбирать угол на основе непрерывного измерения коэффициента пропускания.

В нижней части диапазона мутности метод спектроскопии усиленного рассеяния в полости ^[6] использует интегрирующий резонатор для удлинения пути фотонов через квазинерассеивающие образцы. В отличие от обычных инструментов DLS, этот метод не зависит от угла, поскольку он исследует образцы изотропно со всех направлений.

Несмотря на то, что измерение DLS с использованием одноуглового детектирования было наиболее распространенным методом, его применение во многих системах научного и промышленного значения было ограничено из-за часто встречающегося многократного рассеяния, при котором фотоны многократно рассеиваются образцом, прежде чем попасть в него. обнаружен. Точная интерпретация становится чрезвычайно сложной для систем с существенным вкладом многократного рассеяния. Это ограничивает метод очень низкими концентрациями частиц, особенно для более крупных частиц и частиц с высоким контрастом показателя преломления, и поэтому большое разнообразие систем исключается из исследований с динамическим рассеянием света. Однако, как показал Шетцель, ^[7] в экспериментах по динамическому рассеянию света можно подавить многократное рассеяние с помощью подхода кросс-корреляции. Общая идея состоит в том, чтобы изолировать однократно рассеянный свет и подавить нежелательный вклад от многократного рассеяния в эксперименте по динамическому рассеянию света. Были разработаны и применены различные реализации кросс-корреляционного рассеяния света. В настоящее время наиболее широко используемой схемой является так называемый метод 3D-динамического рассеяния света. ^[8]^[9] Тот же метод можно также использовать для коррекции данных статического рассеяния света за счет многократного рассеяния. ^[10] Альтернативно, в пределе сильного многократного рассеяния, вариант динамического рассеяния света, называемый спектроскопией диффузных волн можно применить .

Анализ данных

Введение

После того как данные автокорреляции сгенерированы, для получения из них «информации» можно использовать различные математические подходы. Анализ рассеяния облегчается, когда частицы не взаимодействуют посредством столкновений или электростатических сил между ионами. Столкновения между частицами можно подавить путем разбавления, а эффекты заряда уменьшаются за счет использования солей для коллапса двойного электрического слоя .

Самый простой подход — рассматривать автокорреляционную функцию первого порядка как одиночный экспоненциальный затух. Это подходит для монодисперсной популяции.

\ g^{1}(q;\tau )=\exp(-\Gamma \tau )\,

где $Γ$ – скорость затухания. Коэффициент поступательной диффузии $D t$ может быть получен для одного угла или для диапазона углов в зависимости от волнового вектора $q$ .

\ \Gamma =q^{2}D_{t}\,

с

\ q={\frac {4\pi n_{0}}{\lambda }}\sin \left({\frac {\theta }{2}}\right)

где $λ$ — длина волны падающего лазера, $n 0$ растворителя — показатель преломления и $θ$ — угол, под которым детектор расположен по отношению к ячейке с образцом.

Показатель преломления растворителя играет решающую роль в рассеянии света и важен для расчета радиуса Стокса по уравнению Стокса-Эйнштейна . ^[11]^[12]^[13] Поэтому предыдущие данные о показателе преломления рассеивающей среды следует оценивать с помощью специальных инструментов, известных как рефрактометры . Альтернативно, приборы DLS, содержащие модуль измерения показателя преломления, позволяют получить хорошую оценку этого важного параметра в пределах ±0,5%, что соответствует точности, определенной стандартом ISO 22412:2017. ^[14]^[15] для значений показателя преломления, необходимых для DLS. Помимо показателя преломления среды, показатель преломления частиц необходим только при анализе частиц большего размера (обычно более 100 нм) и необходимы объемные или численно-взвешенные распределения по размерам. требуется предварительное знание показателя преломления и поглощения материала В этих случаях для применения рассеяния Ми . ^[16]^[17]

В зависимости от анизотропии и полидисперсности системы результирующий график $(Γ/ q 2)$ против $q 2$ может иметь или не иметь угловую зависимость. Маленькие сферические частицы не будут иметь угловой зависимости и, следовательно, не будут иметь анизотропии. График $(Γ/ q 2)$ против $q 2$ получится горизонтальная линия. Частицы с формой, отличной от сферы, будут демонстрировать анизотропию и, следовательно, угловую зависимость при построении графика $(Γ/ q 2)$ против $q 2$ . ^[18] Перехватом в любом случае будет D _t . существует оптимальный угол обнаружения $θ$ Таким образом, для каждого размера частиц . Качественный анализ всегда необходимо проводить при нескольких углах рассеяния (многоугловая ДРС). Это становится еще более важным в полидисперсном образце с неизвестным гранулометрическим составом. Под определенными углами интенсивность рассеяния некоторых частиц будет полностью подавлять слабый сигнал рассеяния других частиц, что делает их невидимыми для анализа данных под этим углом. Инструменты DLS, которые работают только под фиксированным углом, могут давать хорошие результаты только для некоторых частиц. Таким образом, указанная точность прибора ДРС только с одним углом обнаружения справедлива только для определенных частиц.

$D t$ часто используется для расчета гидродинамического радиуса сферы с помощью уравнения Стокса – Эйнштейна. Важно отметить, что размер, определяемый динамическим рассеянием света, представляет собой размер сферы, которая движется так же, как и рассеиватель. Так, например, если рассеиватель представляет собой случайный клубок полимера, определенный размер не совпадает с радиусом вращения, определяемым статическим рассеянием света . Также полезно отметить, что полученный размер будет включать любые другие молекулы или молекулы растворителя, которые движутся вместе с частицей. Так, например, коллоидное золото со слоем ПАВ будет казаться больше при динамическом рассеянии света (включая слой ПАВ), чем при просвечивающей электронной микроскопии (которая не «видит» слой из-за плохого контраста).

В большинстве случаев образцы являются полидисперсными. Таким образом, автокорреляционная функция представляет собой сумму экспоненциальных спадов, соответствующих каждому виду в популяции.

g^{1}(q;\tau )=\sum _{i=1}^{n}G_{i}(\Gamma _{i})\exp(-\Gamma _{i}\tau )=\int G(\Gamma )\exp(-\Gamma \tau )\,d\Gamma .

Заманчиво получить данные для $g 1 (q; τ)$ и попытайтесь инвертировать приведенное выше, чтобы извлечь $G (Γ)$ . Поскольку $G (Γ)$ пропорциональна относительному рассеянию каждого вида, она содержит информацию о распределении размеров. Однако это известно как некорректная задача. Описанные ниже методы (и другие) были разработаны для извлечения как можно большего количества полезной информации из автокорреляционной функции.

Метод накопления

Одним из наиболее распространенных методов является кумулятивный метод. ^[19]^[20] из чего, помимо суммы приведенных выше экспонент, можно получить дополнительную информацию о дисперсии системы следующим образом:

\ g^{1}(q;\tau )=\exp \left(-{\bar {\Gamma }}\left(\tau -{\frac {\mu _{2}}{2!}}\tau ^{2}+{\frac {\mu _{3}}{3!}}\tau ^{3}+\cdots \right)\right)

где $Γ$ — средняя скорость затухания и $µ 2 / Γ 2$ – индекс полидисперсности второго порядка (или показатель дисперсии). третьего порядка Можно также получить индекс полидисперсности , но это необходимо только в том случае, если частицы системы обладают высокой полидисперсностью. Усредненный по z коэффициент поступательной диффузии $D z$ может быть получен для одного угла или для диапазона углов в зависимости от волнового вектора $q$ .

\ {\bar {\Gamma }}=q^{2}D_{z}\,

Следует отметить, что кумулянтный метод справедлив при малых $τ$ и достаточно узкой $G (Γ)$ . ^[21] Редко следует использовать параметры, выходящие за пределы µ ₃ , поскольку переобучение данных многими параметрами в разложении степенного ряда приведет к отображению всех параметров, включая $\scriptstyle {\bar {\Gamma }}$ и μ ₂ менее точны. ^[22]На кумулянтный метод гораздо меньше влияет экспериментальный шум, чем на методы, описанные ниже.

Функция распределения по размерам

Распределение частиц по размерам также можно получить с помощью автокорреляционной функции. Однако полидисперсные образцы плохо разрешаются с помощью анализа кумулянтного соответствия. Таким образом, комбинация алгоритмов неотрицательных наименьших квадратов (NNLS) с методами регуляризации, такими как регуляризация Тихонова , может использоваться для разрешения мультимодальных выборок. ^[16] Важной особенностью оптимизации NNLS является термин регуляризации, используемый для идентификации конкретных решений и минимизации отклонения между данными измерения и подгонкой. Не существует идеального термина регуляризации, подходящего для всех выборок. Форма этого члена может определить, будет ли решение представлять собой общее широкое распределение с небольшим количеством пиков или же подойдут узкие и дискретные популяции. Альтернативно расчет распределения частиц по размерам выполняется с использованием алгоритма CONTIN.

Алгоритм CONTIN

Альтернативный метод анализа автокорреляционной функции может быть реализован с помощью обратного преобразования Лапласа, известного как CONTIN, разработанного Стивеном Провенчером. ^[23]^[24] Анализ CONTIN идеален для гетеродисперсных , полидисперсных и мультимодальных систем, которые не могут быть решены кумулянтным методом. Разрешение разделения двух разных популяций частиц составляет примерно пять или более раз, а разница в относительных интенсивностях между двумя разными популяциями должна быть менее 1:10. ⁻⁵.

Метод максимальной энтропии

Метод максимальной энтропии – это метод анализа, имеющий большой потенциал развития. Этот метод также используется для количественной оценки о скорости седиментации, данных полученных при аналитическом ультрацентрифугировании . Метод максимальной энтропии включает в себя несколько итерационных шагов, чтобы минимизировать отклонение подобранных данных от экспериментальных данных и впоследствии уменьшить χ ² подобранных данных.

Рассеяние несферических частиц

Если рассматриваемая частица не имеет сферической формы, необходимо учитывать и вращательное движение, поскольку рассеяние света будет различным в зависимости от ориентации. По мнению Пекоры, вращательное броуновское движение будет влиять на рассеяние, когда частица удовлетворяет двум условиям; они должны быть как оптически, так и геометрически анизотропными. ^[25] Молекулы в форме стержней отвечают этим требованиям, поэтому в дополнение к коэффициенту поступательной диффузии необходимо учитывать коэффициент вращательной диффузии. В наиболее краткой форме уравнение выглядит так:

{\frac {A}{B}}={\frac {5}{4}}{\frac {4\mathrm {M} _{p}+2\mathrm {N} \mathrm {M} _{l}\mathrm {M} _{p}+\mathrm {M} _{l}}{\mathrm {M} _{p}-\mathrm {N} +\mathrm {M} _{l}}}

Где $A / B$ — соотношение двух мод релаксации (поступательной и вращательной), $M p$ содержит информацию об оси, перпендикулярной центральной оси частицы, а $M l$ содержит информацию об оси, параллельной центральной оси.

В 2007 году Питер Р. Ланг и его команда решили использовать динамическое рассеяние света для определения длины частиц и соотношения сторон коротких золотых наностержней. ^[26] Они выбрали этот метод, поскольку он не разрушает образец и его относительно легко настроить. Оба состояния релаксации наблюдались в геометрии VV, и коэффициенты диффузии обоих движений были использованы для расчета аспектных соотношений наночастиц золота.

Приложения

DLS используется для характеристики размера различных частиц, включая белки, ^[27] полимеры, мицеллы, ^[28] Белковые клетки и вирусоподобные частицы, ^[29]^[30] везикулы, ^[31] углеводы, наночастицы, биологические клетки, ^[32] и гели. ^[33] Если система не является дисперсной по размеру, можно определить средний эффективный диаметр частиц. Это измерение зависит от размера ядра частицы, размера поверхностных структур, концентрации частиц и типа ионов в среде.

Поскольку DLS по существу измеряет флуктуации интенсивности рассеянного света из-за диффундирующих частиц, можно определить коэффициент диффузии частиц. Программное обеспечение DLS коммерческих приборов обычно отображает популяцию частиц разного диаметра. Если система монодисперсная, должна быть только одна популяция, тогда как в полидисперсной системе будет несколько популяций частиц. Если в образце присутствует популяция более чем одного размера, то для инструментов фотонной корреляционной спектроскопии следует применять либо анализ CONTIN, либо для приборов с доплеровским сдвигом следует применять метод спектра мощности.

Исследования стабильности можно удобно проводить с помощью DLS. Периодические измерения DLS образца могут показать, агрегируют ли частицы с течением времени, наблюдая за тем, увеличивается ли гидродинамический радиус частицы. Если частицы агрегируются, будет большая популяция частиц с большим радиусом. В некоторых машинах DLS стабильность в зависимости от температуры можно анализировать путем контроля температуры на месте .

См. также

Ссылки

^ Берн, БиДжей; Пекора, Р. Динамическое рассеяние света . Публикации Курьера Дувра (2000) ISBN 0-486-41155-9
^ Чу, Б. (1 января 1970 г.). «Лазерное рассеяние света». Ежегодный обзор физической химии . 21 (1): 145–174. Бибкод : 1970ARPC...21..145C . дои : 10.1146/annurev.pc.21.100170.001045 .
^ Пекора, Р. (1964). «Доплеровские сдвиги при рассеянии света чистыми жидкостями и растворами полимеров». Журнал химической физики . 40 (6): 1604. Бибкод : 1964ЖЧФ..40.1604П . дои : 10.1063/1.1725368 .
^ Гудман, Дж (1976). «Некоторые фундаментальные свойства спекла». J. Опт. Соц. Являюсь . 66 (11): 1145–1150. Бибкод : 1976JOSA...66.1145G . дои : 10.1364/josa.66.001145 .
^ «Множественные углы обнаружения в анализе динамического рассеяния света :: Anton Paar Wiki» . Антон Паар (на немецком языке) . Проверено 31 мая 2022 г.
^ Грасиани, Гийом; Кинг, Джон Т.; Амблар, Франсуа (30 августа 2022 г.). «Спектроскопия резонаторного рассеяния выявляет динамику белков и наночастиц в квазипрозрачных и миниатюрных образцах» . АСУ Нано . 16 (10): 16796–16805. arXiv : 2111.09616 . дои : 10.1021/acsnano.2c06471 . ISSN 1936-0851 . ПМИД 36039927 . S2CID 244345602 .
^ Шетцель, К. (1991). «Подавление многократного рассеяния с помощью методов взаимной корреляции фотонов» (PDF) . Дж. Мод. Опц . 38 : 1849. Бибкод : 1990JPCM....2..393S . дои : 10.1088/0953-8984/2/S/062 . S2CID 250745836 . Проверено 7 апреля 2014 г.
^ Урбан, К.; Шуртенбергер, П. (1998). «Характеристика мутных коллоидных суспензий с использованием методов светорассеяния в сочетании с методами взаимной корреляции». J. Наука о коллоидном интерфейсе . 207 (1): 150–158. Бибкод : 1998JCIS..207..150U . дои : 10.1006/jcis.1998.5769 . ПМИД 9778402 .
^ Блок, И.; Шеффолд, Ф. (2010). «Модулированное трехмерное кросс-корреляционное рассеяние света: улучшение характеристик мутных образцов». Обзор научных инструментов . 81 (12): 123107–123107–7. arXiv : 1008.0615 . Бибкод : 2010RScI...81l3107B . дои : 10.1063/1.3518961 . ПМИД 21198014 . S2CID 9240166 .
^ Пьюзи, ПН (1999). «Подавление многократного рассеяния методами взаимной корреляции фотонов». Текущее мнение в области коллоидной и интерфейсной науки . 4 (3): 177–185. дои : 10.1016/S1359-0294(99)00036-9 .
^ Стратт, JW (1 июня 1871 г.). «LVIII. О рассеянии света малыми частицами» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 41 (275): 447–454. дои : 10.1080/14786447108640507 . ISSN 1941-5982 .
^ Стратт, JW (1 апреля 1871 г.). «XXXVI. О свете неба, его поляризации и цвете» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 41 (273): 274–279. дои : 10.1080/14786447108640479 . ISSN 1941-5982 .
^ Штетефельд, Йорг; Маккенна, Шон А.; Патель, Трушар Р. (1 декабря 2016 г.). «Динамическое рассеяние света: практическое руководство и приложения в биомедицинских науках» . Биофизические обзоры . 8 (4): 409–427. дои : 10.1007/s12551-016-0218-6 . ISSN 1867-2469 . ПМК 5425802 . ПМИД 28510011 .
^ «ISO 22412:2017. Анализ размера частиц. Динамическое светорассеяние (ДРС)» . ИСО . Проверено 31 мая 2022 г.
^ Тарек, Сайед Мохаммед; Бучуэн, Армель; Рой, Шувашиш; Циммерман, Делл; Джур, Гитапун; Бати, Джеджал Редди; Палчоудхури, Субантика (август 2021 г.). «Подход к динамическому рассеянию света для обнаружения наноматериалов в реке Теннесси» . Исследования водных ресурсов . 57 (8). Бибкод : 2021WRR....5728687T . дои : 10.1029/2020WR028687 . ISSN 0043-1397 . S2CID 238831573 .
^ Перейти обратно: ^а ^б «Белая книга: понимание концепции динамического рассеяния света :: Anton-Paar.com» . Антон Паар . Проверено 31 мая 2022 г.
^ Альфано, Бригида; Барретта, Луиджи; Дель Джудиче, Антонио; Де Вито, Саверио; Из Франции Джироламо; Эспозито, Елена; Формизано, Фабрицио; Массера, Этторе; Миглиетта, Мария Люсия; Поличетти, Тициана (29 ноября 2020 г.). «Обзор недорогих датчиков твердых частиц с точки зрения разработчиков» . Датчики . 20 (23): 6819. Бибкод : 2020Senso..20.6819A . дои : 10.3390/s20236819 . ISSN 1424-8220 . ПМЦ 7730878 . ПМИД 33260320 .
^ Гои, Жан-Франсуа; Варшни, Сунил К.; Жером, Роберт (2001). «Водорастворимые комплексы, образованные сополимерами поли(2-винилпиридиния)-блок-поли(этиленоксид) и поли(метакрилата натрия)-блок-поли(этиленоксид)». Макромолекулы . 34 (10): 3361. Бибкод : 2001МаМол..34.3361Г . дои : 10.1021/ma0020483 .
^ Коппель, Деннис Э. (1972). «Анализ макромолекулярной полидисперсности в корреляционной спектроскопии интенсивности: метод кумулянтов». Журнал химической физики . 57 (11): 4814–4820. Бибкод : 1972ЖЧФ..57.4814К . дои : 10.1063/1.1678153 .
^ Фрискен, Барбара Дж. (2001). «Возвращаясь к методу кумулянтов для анализа данных динамического светорассеяния» (PDF) . Прикладная оптика . 40 (24): 4087–91. Бибкод : 2001ApOpt..40.4087F . дои : 10.1364/AO.40.004087 . ПМИД 18360445 .
^ Хасан, Пенсильвания; Кулшрешта, Сквер (август 2006 г.). «Модификация к кумулянтному анализу полидисперсности в данных квазиупругого светорассеяния». Журнал коллоидной и интерфейсной науки . 300 (2): 744–8. Бибкод : 2006JCIS..300..744H . doi : 10.1016/j.jcis.2006.04.013 . ISSN 0021-9797 . ПМИД 16790246 .
^ Чу, Б (1992). Рассеяние лазерного света: основные принципы и практика . Академическая пресса. ISBN 978-0-12-174551-6 .
^ Провенчер, С. (1982). «CONTIN: программа регуляризации общего назначения с ограничениями для обращения зашумленных линейных алгебраических и интегральных уравнений» (PDF) . Компьютерная физика. Коммуникации . 27 (3): 229–242. Бибкод : 1982CoPhC..27..229P . дои : 10.1016/0010-4655(82)90174-6 .
^ Провеншер, Юго-Запад (1982). «Метод ограниченной регуляризации для инвертирования данных, представленных линейными алгебраическими или интегральными уравнениями» (PDF) . Вычислить. Физ. Коммун . 27 (3): 213–227. Бибкод : 1982CoPhC..27..213P . дои : 10.1016/0010-4655(82)90173-4 .
^ Арагон, СР; Пекора, Р. (1976). «Теория динамического рассеяния света полидисперсными системами». Журнал химической физики . 64 (6): 2395. Бибкод : 1976ЖЧФ..64.2395А . дои : 10.1063/1.432528 .
^ Родригес-Фернандес, Дж.; Перес-Жюсте, Дж.; Лиз-Марзан, LM; Ланг, PR (2007). «Динамическое рассеяние света короткими стержнями из золота с низким соотношением сторон» (PDF) . Журнал физической химии . 111 (13): 5020–5025. дои : 10.1021/jp067049x .
^ Долинска, Моника Б.; Янг, Кеннет Л.; Кассуф, Клаудия; Димитриадис, Эмилиос К.; Вингфилд, Пол Т.; Сергеев Юрий В. (3 января 2020 г.). «Стабильность белка и функциональная характеристика внутримеланосомного домена человеческого рекомбинантного белка, родственного тирозиназе 1» . Международный журнал молекулярных наук . 21 (1): 331. doi : 10.3390/ijms21010331 . ISSN 1422-0067 . ПМЦ 6981619 . ПМИД 31947795 .
^ Бхут, Партх Раджешкумар; Пал, Ниланджан; Мандал, Аджай (3 декабря 2019 г.). «Характеристика гидрофобно модифицированного полиакриламида в смешанных системах полимер-гемини-ПАВ для повышения нефтеотдачи» . АСУ Омега . 4 (23): 20164–20177. дои : 10.1021/acsomega.9b02279 . ISSN 2470-1343 . ПМК 6893946 . ПМИД 31815217 .
^ Вагвани Х.К., Дуглас Т. (март 2021 г.). «Цитохром С с пероксидазоподобной активностью, инкапсулированный внутри небольшой наноклетки белка DPS» . Журнал химии материалов Б. 9 (14): 3168–3179. дои : 10.1039/d1tb00234a . ПМИД 33885621 .
^ Вагвани Х.К., Учида М., Дуглас Т. (апрель 2020 г.). «Вирусоподобные частицы (ВЛП) как платформа для иерархической компартментализации» . Биомакромолекулы . 21 (6): 2060–2072. doi : 10.1021/acs.biomac.0c00030 . ПМИД 32319761 .
^ Велу, Сабариш КП; Ян, Минхао; Ценг, Куо-Пи; Вонг, Кен-Цунг; Бассани, Дарио М.; Терех, Пьер (6 февраля 2013 г.). «Спонтанное образование искусственных везикул в органических средах за счет взаимодействий водородных связей». Макромолекулы . 46 (4): 1591–1598. Бибкод : 2013МаМол..46.1591В . дои : 10.1021/ma302595g .
^ Йена, Сидхартха С.; Джоши, Хирен М.; Сабариш, КПВ; Тата, БВР; Рао, ТС (2006). «Динамика Deinococcus radiodurans в условиях контролируемого роста» . Биофизический журнал . 91 (7): 2699–2707. Бибкод : 2006BpJ....91.2699J . doi : 10.1529/biophysj.106.086520 . ПМЦ 1562370 . ПМИД 16829564 .
^ Сабариш, КПВ; Йена, Сидхартха С.; Тата, BVR (5 мая 2006 г.). «Исследования динамического светорассеяния на фотополимеризованных и химически сшитых полиакриламидных гидрогелях». Материалы конференции AIP . 832 (1): 307–310. Бибкод : 2006AIPC..832..307S . дои : 10.1063/1.2204513 . ISSN 0094-243X .

Внешние ссылки

[1] Берн, БиДжей; Пекора, Р. Динамическое рассеяние света . Публикации Курьера Дувра (2000) ISBN 0-486-41155-9

[2] Чу, Б. (1 января 1970 г.). «Лазерное рассеяние света». Ежегодный обзор физической химии . 21 (1): 145–174. Бибкод : 1970ARPC...21..145C . дои : 10.1146/annurev.pc.21.100170.001045 .

[3] Пекора, Р. (1964). «Доплеровские сдвиги при рассеянии света чистыми жидкостями и растворами полимеров». Журнал химической физики . 40 (6): 1604. Бибкод : 1964ЖЧФ..40.1604П . дои : 10.1063/1.1725368 .

[4] Гудман, Дж (1976). «Некоторые фундаментальные свойства спекла». J. Опт. Соц. Являюсь . 66 (11): 1145–1150. Бибкод : 1976JOSA...66.1145G . дои : 10.1364/josa.66.001145 .

[5] «Множественные углы обнаружения в анализе динамического рассеяния света :: Anton Paar Wiki» . Антон Паар (на немецком языке) . Проверено 31 мая 2022 г.

[6] Грасиани, Гийом; Кинг, Джон Т.; Амблар, Франсуа (30 августа 2022 г.). «Спектроскопия резонаторного рассеяния выявляет динамику белков и наночастиц в квазипрозрачных и миниатюрных образцах» . АСУ Нано . 16 (10): 16796–16805. arXiv : 2111.09616 . дои : 10.1021/acsnano.2c06471 . ISSN 1936-0851 . ПМИД 36039927 . S2CID 244345602 .

[7] Шетцель, К. (1991). «Подавление многократного рассеяния с помощью методов взаимной корреляции фотонов» (PDF) . Дж. Мод. Опц . 38 : 1849. Бибкод : 1990JPCM....2..393S . дои : 10.1088/0953-8984/2/S/062 . S2CID 250745836 . Проверено 7 апреля 2014 г.

[8] Урбан, К.; Шуртенбергер, П. (1998). «Характеристика мутных коллоидных суспензий с использованием методов светорассеяния в сочетании с методами взаимной корреляции». J. Наука о коллоидном интерфейсе . 207 (1): 150–158. Бибкод : 1998JCIS..207..150U . дои : 10.1006/jcis.1998.5769 . ПМИД 9778402 .

[9] Блок, И.; Шеффолд, Ф. (2010). «Модулированное трехмерное кросс-корреляционное рассеяние света: улучшение характеристик мутных образцов». Обзор научных инструментов . 81 (12): 123107–123107–7. arXiv : 1008.0615 . Бибкод : 2010RScI...81l3107B . дои : 10.1063/1.3518961 . ПМИД 21198014 . S2CID 9240166 .

[10] Пьюзи, ПН (1999). «Подавление многократного рассеяния методами взаимной корреляции фотонов». Текущее мнение в области коллоидной и интерфейсной науки . 4 (3): 177–185. дои : 10.1016/S1359-0294(99)00036-9 .

[11] Стратт, JW (1 июня 1871 г.). «LVIII. О рассеянии света малыми частицами» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 41 (275): 447–454. дои : 10.1080/14786447108640507 . ISSN 1941-5982 .

[12] Стратт, JW (1 апреля 1871 г.). «XXXVI. О свете неба, его поляризации и цвете» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 41 (273): 274–279. дои : 10.1080/14786447108640479 . ISSN 1941-5982 .

[13] Штетефельд, Йорг; Маккенна, Шон А.; Патель, Трушар Р. (1 декабря 2016 г.). «Динамическое рассеяние света: практическое руководство и приложения в биомедицинских науках» . Биофизические обзоры . 8 (4): 409–427. дои : 10.1007/s12551-016-0218-6 . ISSN 1867-2469 . ПМК 5425802 . ПМИД 28510011 .

[14] «ISO 22412:2017. Анализ размера частиц. Динамическое светорассеяние (ДРС)» . ИСО . Проверено 31 мая 2022 г.

[15] Тарек, Сайед Мохаммед; Бучуэн, Армель; Рой, Шувашиш; Циммерман, Делл; Джур, Гитапун; Бати, Джеджал Редди; Палчоудхури, Субантика (август 2021 г.). «Подход к динамическому рассеянию света для обнаружения наноматериалов в реке Теннесси» . Исследования водных ресурсов . 57 (8). Бибкод : 2021WRR....5728687T . дои : 10.1029/2020WR028687 . ISSN 0043-1397 . S2CID 238831573 .

[:0-16] Перейти обратно: ^а ^б «Белая книга: понимание концепции динамического рассеяния света :: Anton-Paar.com» . Антон Паар . Проверено 31 мая 2022 г.

[17] Альфано, Бригида; Барретта, Луиджи; Дель Джудиче, Антонио; Де Вито, Саверио; Из Франции Джироламо; Эспозито, Елена; Формизано, Фабрицио; Массера, Этторе; Миглиетта, Мария Люсия; Поличетти, Тициана (29 ноября 2020 г.). «Обзор недорогих датчиков твердых частиц с точки зрения разработчиков» . Датчики . 20 (23): 6819. Бибкод : 2020Senso..20.6819A . дои : 10.3390/s20236819 . ISSN 1424-8220 . ПМЦ 7730878 . ПМИД 33260320 .

[18] Гои, Жан-Франсуа; Варшни, Сунил К.; Жером, Роберт (2001). «Водорастворимые комплексы, образованные сополимерами поли(2-винилпиридиния)-блок-поли(этиленоксид) и поли(метакрилата натрия)-блок-поли(этиленоксид)». Макромолекулы . 34 (10): 3361. Бибкод : 2001МаМол..34.3361Г . дои : 10.1021/ma0020483 .

[19] Коппель, Деннис Э. (1972). «Анализ макромолекулярной полидисперсности в корреляционной спектроскопии интенсивности: метод кумулянтов». Журнал химической физики . 57 (11): 4814–4820. Бибкод : 1972ЖЧФ..57.4814К . дои : 10.1063/1.1678153 .

[20] Фрискен, Барбара Дж. (2001). «Возвращаясь к методу кумулянтов для анализа данных динамического светорассеяния» (PDF) . Прикладная оптика . 40 (24): 4087–91. Бибкод : 2001ApOpt..40.4087F . дои : 10.1364/AO.40.004087 . ПМИД 18360445 .

[21] Хасан, Пенсильвания; Кулшрешта, Сквер (август 2006 г.). «Модификация к кумулянтному анализу полидисперсности в данных квазиупругого светорассеяния». Журнал коллоидной и интерфейсной науки . 300 (2): 744–8. Бибкод : 2006JCIS..300..744H . doi : 10.1016/j.jcis.2006.04.013 . ISSN 0021-9797 . ПМИД 16790246 .

[22] Чу, Б (1992). Рассеяние лазерного света: основные принципы и практика . Академическая пресса. ISBN 978-0-12-174551-6 .

[23] Провенчер, С. (1982). «CONTIN: программа регуляризации общего назначения с ограничениями для обращения зашумленных линейных алгебраических и интегральных уравнений» (PDF) . Компьютерная физика. Коммуникации . 27 (3): 229–242. Бибкод : 1982CoPhC..27..229P . дои : 10.1016/0010-4655(82)90174-6 .

[24] Провеншер, Юго-Запад (1982). «Метод ограниченной регуляризации для инвертирования данных, представленных линейными алгебраическими или интегральными уравнениями» (PDF) . Вычислить. Физ. Коммун . 27 (3): 213–227. Бибкод : 1982CoPhC..27..213P . дои : 10.1016/0010-4655(82)90173-4 .

[25] Арагон, СР; Пекора, Р. (1976). «Теория динамического рассеяния света полидисперсными системами». Журнал химической физики . 64 (6): 2395. Бибкод : 1976ЖЧФ..64.2395А . дои : 10.1063/1.432528 .

[26] Родригес-Фернандес, Дж.; Перес-Жюсте, Дж.; Лиз-Марзан, LM; Ланг, PR (2007). «Динамическое рассеяние света короткими стержнями из золота с низким соотношением сторон» (PDF) . Журнал физической химии . 111 (13): 5020–5025. дои : 10.1021/jp067049x .

[27] Долинска, Моника Б.; Янг, Кеннет Л.; Кассуф, Клаудия; Димитриадис, Эмилиос К.; Вингфилд, Пол Т.; Сергеев Юрий В. (3 января 2020 г.). «Стабильность белка и функциональная характеристика внутримеланосомного домена человеческого рекомбинантного белка, родственного тирозиназе 1» . Международный журнал молекулярных наук . 21 (1): 331. doi : 10.3390/ijms21010331 . ISSN 1422-0067 . ПМЦ 6981619 . ПМИД 31947795 .

[28] Бхут, Партх Раджешкумар; Пал, Ниланджан; Мандал, Аджай (3 декабря 2019 г.). «Характеристика гидрофобно модифицированного полиакриламида в смешанных системах полимер-гемини-ПАВ для повышения нефтеотдачи» . АСУ Омега . 4 (23): 20164–20177. дои : 10.1021/acsomega.9b02279 . ISSN 2470-1343 . ПМК 6893946 . ПМИД 31815217 .

[29] Вагвани Х.К., Дуглас Т. (март 2021 г.). «Цитохром С с пероксидазоподобной активностью, инкапсулированный внутри небольшой наноклетки белка DPS» . Журнал химии материалов Б. 9 (14): 3168–3179. дои : 10.1039/d1tb00234a . ПМИД 33885621 .

[30] Вагвани Х.К., Учида М., Дуглас Т. (апрель 2020 г.). «Вирусоподобные частицы (ВЛП) как платформа для иерархической компартментализации» . Биомакромолекулы . 21 (6): 2060–2072. doi : 10.1021/acs.biomac.0c00030 . ПМИД 32319761 .

[31] Велу, Сабариш КП; Ян, Минхао; Ценг, Куо-Пи; Вонг, Кен-Цунг; Бассани, Дарио М.; Терех, Пьер (6 февраля 2013 г.). «Спонтанное образование искусственных везикул в органических средах за счет взаимодействий водородных связей». Макромолекулы . 46 (4): 1591–1598. Бибкод : 2013МаМол..46.1591В . дои : 10.1021/ma302595g .

[32] Йена, Сидхартха С.; Джоши, Хирен М.; Сабариш, КПВ; Тата, БВР; Рао, ТС (2006). «Динамика Deinococcus radiodurans в условиях контролируемого роста» . Биофизический журнал . 91 (7): 2699–2707. Бибкод : 2006BpJ....91.2699J . doi : 10.1529/biophysj.106.086520 . ПМЦ 1562370 . ПМИД 16829564 .

[33] Сабариш, КПВ; Йена, Сидхартха С.; Тата, BVR (5 мая 2006 г.). «Исследования динамического светорассеяния на фотополимеризованных и химически сшитых полиакриламидных гидрогелях». Материалы конференции AIP . 832 (1): 307–310. Бибкод : 2006AIPC..832..307S . дои : 10.1063/1.2204513 . ISSN 0094-243X .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]