Эффект Доплера


Эффект Доплера (также Доплеровский сдвиг — это изменение частоты волны по ) отношению к наблюдателю, который движется относительно источника волны. [1] [2] [3] Эффект Доплера назван в честь физика Кристиана Доплера , который описал это явление в 1842 году. Типичным примером доплеровского сдвига является изменение высоты звука, слышимое, когда транспортное средство , подающее звуковой сигнал, приближается и удаляется от наблюдателя. По сравнению с излучаемой частотой принимаемая частота выше при сближении, одинакова в момент прохождения и ниже при спуске. [4]
Когда источник звуковой волны движется к наблюдателю, каждый последующий цикл волны излучается из положения, более близкого к наблюдателю, чем предыдущий цикл. [4] [5] Следовательно, с точки зрения наблюдателя, время между циклами сокращается, а это означает, что частота увеличивается. И наоборот, если источник звуковой волны удаляется от наблюдателя, каждый цикл волны излучается из положения, более удаленного от наблюдателя, чем предыдущий цикл, поэтому время прихода между последовательными циклами увеличивается, тем самым уменьшая частоту.
Для волн, распространяющихся в среде, таких как звуковые волны, скорость наблюдателя и источника зависит от среды, в которой передаются волны. [3] Таким образом, общий эффект Доплера в таких случаях может быть результатом движения источника, движения наблюдателя, движения среды или любой их комбинации. Для волн, распространяющихся в вакууме , как это возможно для электромагнитных волн или гравитационных волн , необходимо учитывать только разницу в скорости между наблюдателем и источником.
История
[ редактировать ]
Впервые этот эффект был предложен Допплером в 1842 году в трактате « и некоторых других звезд О цветном свете двойных звезд неба». [6] Гипотеза была проверена на звуковых волнах Байсом Баллотом в 1845 году. [стр 1] звука Он подтвердил, что высота была выше излучаемой частоты, когда источник звука приближался к нему, и ниже, чем излучаемая частота, когда источник звука удалялся от него. Ипполит Физо независимо открыл то же явление на электромагнитных волнах в 1848 году (во Франции этот эффект иногда называют «эффектом Доплера-Физо», но это название не было принято в остальном мире, поскольку открытие Физо произошло через шесть лет после предложения Доплера). [стр 2] [7] В Великобритании Джон Скотт Рассел провел экспериментальное исследование эффекта Доплера (1848 г.). [стр. 3]
Общий
[ редактировать ]В классической физике, где скорости источника и приемника относительно среды ниже скорости волн в среде, связь между наблюдаемой частотой и излучаемая частота дается: [8] где
- – скорость распространения волн в среде;
- - скорость приемника относительно среды. В формуле добавляется в если приемник движется к источнику, вычитается, если приемник удаляется от источника;
- – скорость источника относительно среды. вычитается из если источник движется к приемнику, добавляется, если источник удаляется от приемника.
Обратите внимание, что это соотношение предсказывает, что частота будет уменьшаться, если источник или приемник удаляются друг от друга.
Аналогично, в предположении, что источник либо приближается, либо удаляется от наблюдателя: где
- – скорость волны относительно приемника;
- – скорость волны относительно источника;
- это длина волны.
Если источник приближается к наблюдателю под углом (но все еще с постоянной скоростью), наблюдаемая частота, которую сначала слышно, выше, чем частота, излучаемая объектом. После этого наблюдается монотонное уменьшение наблюдаемой частоты по мере приближения к наблюдателю, за счет равенства, когда она исходит из направления, перпендикулярного относительному движению (и излучалась в точке наибольшего сближения; но когда волна принимается , источник и наблюдатель больше не будут находиться ближе всего) и продолжающееся монотонное уменьшение по мере удаления от наблюдателя. Когда наблюдатель находится очень близко к траектории объекта, переход от высокой частоты к низкой происходит очень резко. Когда наблюдатель находится далеко от пути объекта, переход от высокой частоты к низкой происходит постепенно.
Если скорости и малы по сравнению со скоростью волны, связь между наблюдаемой частотой и излучаемая частота примерно [8]
| Наблюдаемая частота | Изменение частоты |
|---|---|
где
- противоположна относительной скорости приемника относительно источника: она положительна, когда источник и приемник движутся навстречу друг другу.
Данный
мы делим на
С мы можем заменить, используя в ряд Тейлора разложение усекая все и более высокие условия:
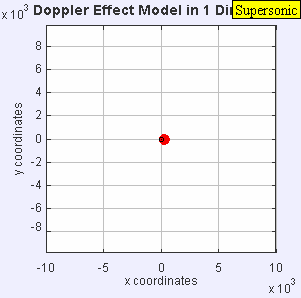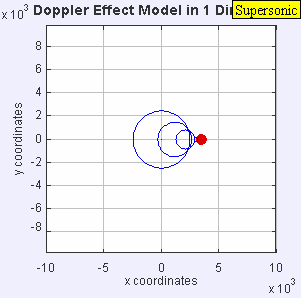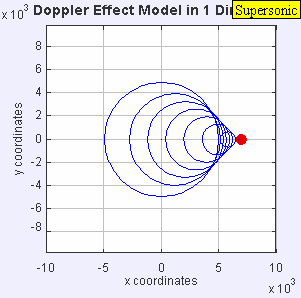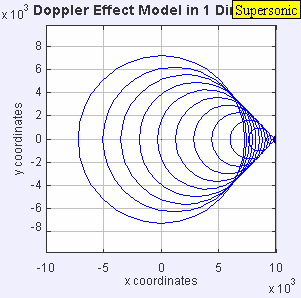
- Стационарный источник звука производит звуковые волны с постоянной частотой f , а волновые фронты распространяются симметрично от источника с постоянной скоростью c. Расстояние между волновыми фронтами — это длина волны. Все наблюдатели будут слышать одну и ту же частоту, которая будет равна фактической частоте источника, где f = f 0 .
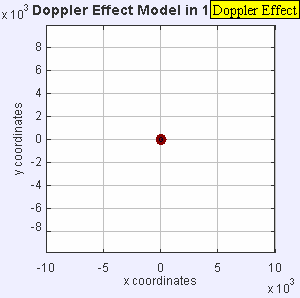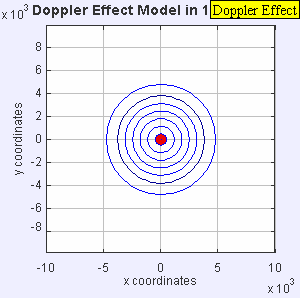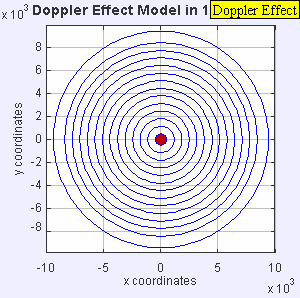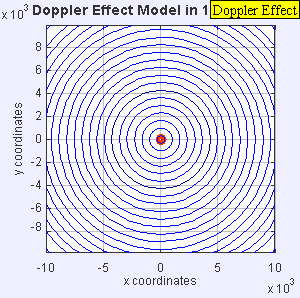
- Один и тот же источник звука излучает звуковые волны с постоянной частотой в одной и той же среде. Однако теперь источник звука движется со скоростью υ s = 0,7 c . Поскольку источник движется, центр каждого нового волнового фронта теперь немного смещается вправо. В результате волновые фронты начинают группироваться с правой стороны (перед) и расходиться дальше с левой стороны (сзади) от источника. Наблюдатель перед источником услышит более высокую частоту f = c + 0 / c – 0,7 c f 0 = 3,33 f 0 и наблюдатель позади источника услышит более низкую частоту f = c - 0 / c + 0,7 c ж 0 знак равно 0,59 ж 0 .
- Теперь источник движется со скоростью звука в среде ( υ s = c ). Волновые фронты перед источником теперь собраны в одной точке. В результате наблюдатель перед источником ничего не обнаружит, пока источник не прибудет, а наблюдатель позади источника услышит более низкую частоту f = c – 0 / c + c ж 0 знак равно 0,5 ж 0 .
- Источник звука теперь превысил скорость звука в среде и движется со скоростью 1,4 c . Поскольку источник движется быстрее, чем создаваемые им звуковые волны, он фактически возглавляет наступающий волновой фронт. Источник звука пройдет мимо неподвижного наблюдателя до того, как наблюдатель услышит звук. В результате наблюдатель перед источником ничего не обнаружит, а наблюдатель за источником услышит более низкую частоту f = c – 0 / c + 1,4 c ж 0 знак равно 0,42 ж 0 .
Последствия
[ редактировать ]Предполагая, что наблюдатель неподвижен, а источник волны движется к наблюдателю со скоростью волны (или превышающей ее), уравнение Доплера предсказывает бесконечную (или отрицательную) частоту с точки зрения наблюдателя. Таким образом, уравнение Доплера для таких случаев неприменимо. Если волна является звуковой волной и источник звука движется быстрее скорости звука, возникающая в результате ударная волна создает звуковой удар .
Лорд Рэлей в своей классической книге о звуке предсказал следующий эффект: если бы наблюдатель двигался от (неподвижного) источника со скоростью, вдвое превышающей скорость звука, музыкальная пьеса, ранее излучаемая этим источником, была бы слышна в правильном темпе и высоте, но при если играть задом наперед . [9]
Приложения
[ редактировать ]Сирены
[ редактировать ]Сирена . на проезжающем автомобиле службы экстренной помощи начнет звучать выше своего стационарного тона, скользить вниз при прохождении и продолжать опускаться ниже своего стационарного тона по мере удаления от наблюдателя Астроном Джон Добсон объяснил этот эффект следующим образом:
Причина, по которой сирена скользит, заключается в том, что она не поражает вас.
Другими словами, если бы сирена приближалась непосредственно к наблюдателю, тон оставался бы постоянным, на более высоком, чем стационарный, уровне до тех пор, пока транспортное средство не столкнется с ним, а затем сразу же перешел бы на новый, более низкий тон. Поскольку транспортное средство проходит мимо наблюдателя, радиальная скорость не остается постоянной, а вместо этого меняется в зависимости от угла между лучом его зрения и скоростью сирены: где - это угол между скоростью движения объекта и линией зрения от объекта до наблюдателя.
Астрономия
[ редактировать ]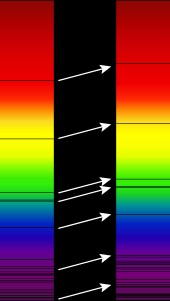
Эффект Доплера для электромагнитных волн, таких как свет, широко используется в астрономии для измерения скорости, с которой звезды и галактики приближаются или удаляются от нас, что приводит к так называемому синему смещению или красному смещению соответственно. Это можно использовать для определения того, является ли кажущаяся одиночной звездой на самом деле тесной двойной системой , для измерения скорости вращения звезд и галактик или для обнаружения экзопланет . Этот эффект обычно происходит в очень небольшом масштабе; невооруженным глазом не было бы заметной разницы в видимом свете. [10] Использование эффекта Доплера в астрономии зависит от знания точных частот дискретных линий в спектрах звезд.
Среди близлежащих звезд наибольшие лучевые скорости относительно Солнца составляют +308 км/с ( BD-15°4041 , также известная как LHS 52, на расстоянии 81,7 световых лет) и −260 км/с ( Вулли 9722 , также известные как Wolf 1106 и LHS 64, на расстоянии 78,2 световых лет). Положительная лучевая скорость означает, что звезда удаляется от Солнца, отрицательная — что она приближается.
Красное смещение также используется для измерения расширения Вселенной . Иногда утверждают, что на самом деле это не эффект Доплера, а возникает из-за расширения пространства. [11] Однако эта картина может ввести в заблуждение, поскольку расширение пространства — это всего лишь математическое соглашение, соответствующее выбору координат . [12] Наиболее естественная интерпретация космологического красного смещения состоит в том, что это действительно доплеровский сдвиг. [13]
Далекие галактики также демонстрируют своеобразное движение , отличное от скорости их космологического удаления. Если красные смещения используются для определения расстояний в соответствии с законом Хаббла , то эти своеобразные движения приводят к искажениям пространства на красных смещениях . [14]
Радар
[ редактировать ]
Эффект Доплера используется в некоторых типах радаров для измерения скорости обнаруженных объектов. Луч радара направляется на движущуюся цель — например, на автомобиль, поскольку полиция использует радар для обнаружения превышения скорости автомобилистами — когда он приближается или удаляется от источника радара. Каждая последующая радиолокационная волна должна пройти большее расстояние, чтобы достичь автомобиля, прежде чем отразится и повторно обнаружиться вблизи источника. Поскольку каждой волне приходится двигаться дальше, промежуток между каждой волной увеличивается, увеличивая длину волны. В некоторых ситуациях луч радара направляется на приближающийся автомобиль, и в этом случае каждая последующая волна проходит меньшее расстояние, уменьшая длину волны. В любой ситуации расчеты на основе эффекта Доплера точно определяют скорость автомобиля. Более того, неконтактный взрыватель , разработанный во время Второй мировой войны, использует доплеровский радар для подрыва взрывчатки в нужное время, на высоте, на нужном расстоянии и т. д. [ нужна ссылка ]
Поскольку доплеровский сдвиг влияет на волну, падающую на цель, а также на волну, отраженную обратно в радар, изменение частоты, наблюдаемое радаром из-за цели, движущейся с относительной скоростью в два раза больше, чем от той же цели, излучающей волну: [15]
Медицинский
[ редактировать ]
Эхокардиограмма . может, в определенных пределах, дать точную оценку направления кровотока и скорости крови и сердечной ткани в любой произвольной точке, используя эффект Доплера Одним из ограничений является то, что ультразвуковой луч должен быть максимально параллелен кровотоку. Измерения скорости позволяют оценить площади и функцию сердечных клапанов, аномальные сообщения между левой и правой половинами сердца, утечку крови через клапаны (клапанную регургитацию) и рассчитать сердечный выброс . Ультразвук с контрастным усилением с использованием газонаполненных микропузырьков контрастного вещества можно использовать для улучшения скорости или других медицинских измерений, связанных с потоком. [16] [17]
Хотя «доплеровский сдвиг» стал синонимом «измерения скорости» в медицинской визуализации, во многих случаях измеряется не частотный сдвиг (доплеровский сдвиг) принятого сигнала, а фазовый сдвиг ( когда полученный сигнал поступает). [стр. 4]
Измерения скорости кровотока также используются в других областях медицинской ультрасонографии , таких как акушерская ультрасонография и неврология . Измерение скорости кровотока в артериях и венах на основе эффекта Доплера является эффективным инструментом для диагностики сосудистых проблем, таких как стеноз . [18]
Измерение расхода
[ редактировать ]Такие инструменты, как лазерный доплеровский велосиметр (LDV) и акустический доплеровский велосиметр (ADV), были разработаны для измерения скорости в потоке жидкости. LDV излучает световой луч, а ADV излучает ультразвуковой акустический импульс и измеряет доплеровский сдвиг длин волн отражений от частиц, движущихся с потоком. Фактический расход рассчитывается как функция скорости и фазы воды. Этот метод позволяет проводить неинтрузивные измерения расхода с высокой точностью и высокой частотой.
Измерение профиля скорости
[ редактировать ]Первоначально разработанная для измерения скорости в медицинских целях (кровоток), ультразвуковая допплеровская скорость (UDV) может измерять в режиме реального времени полный профиль скорости практически в любых жидкостях, содержащих частицы во взвешенном состоянии, такие как пыль, газовые пузырьки, эмульсии. Потоки могут быть пульсирующими, осциллирующими, ламинарными или турбулентными, стационарными или нестационарными. Эта методика полностью неинвазивна.
Спутники
[ редактировать ] | 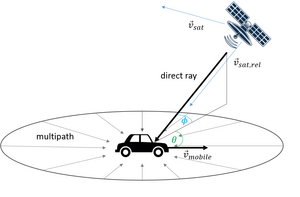 |  |
Спутниковая навигация
[ редактировать ]Доплеровский сдвиг можно использовать для спутниковой навигации, например, в Transit и DORIS .
Спутниковая связь
[ редактировать ]Доплеровский эффект также необходимо компенсировать в спутниковой связи . Быстро движущиеся спутники могут иметь доплеровский сдвиг относительно наземной станции в десятки килогерц. Скорость, а значит и величина эффекта Доплера, меняется из-за кривизны Земли. Динамическая доплеровская компенсация, при которой частота сигнала постепенно изменяется во время передачи, используется для того, чтобы спутник получал сигнал постоянной частоты. [20] После осознания того, что доплеровский сдвиг не учитывался перед запуском зонда «Гюйгенс» в рамках миссии «Кассини-Гюйгенс» в 2005 году , траектория зонда была изменена для приближения к Титану таким образом, чтобы его передачи проходили перпендикулярно направлению его движения относительно Кассини. значительно уменьшая доплеровский сдвиг. [21]
Доплеровский сдвиг прямой траектории можно оценить по следующей формуле: [22] где скорость мобильной станции, длина волны несущей, - угол места спутника и — направление движения относительно спутника.
Дополнительный доплеровский сдвиг из-за перемещения спутника можно описать как: где - относительная скорость спутника.
Аудио
[ редактировать ]Динамик Лесли , который чаще всего ассоциируется и преимущественно используется со знаменитым органом Хаммонда , использует эффект Доплера, используя электродвигатель для вращения акустического рупора вокруг громкоговорителя, посылая звук по кругу. Это приводит к быстрому изменению частоты нот клавиатуры на ухе слушателя.
Измерение вибрации
[ редактировать ]Лазерный доплеровский виброметр (ЛДВ) — бесконтактный прибор для измерения вибрации. Лазерный луч из LDV направляется на интересующую поверхность, а амплитуда и частота вибрации извлекаются из доплеровского сдвига частоты лазерного луча из-за движения поверхности.
Робототехника
[ редактировать ]Динамическое планирование пути в реальном времени в робототехнике, помогающее движению роботов в сложной среде с движущимися препятствиями, часто использует эффект Доплера. [23] Такие приложения специально используются для соревновательной робототехники, где окружающая среда постоянно меняется, например, в робофутболе.
Обратный эффект Доплера
[ редактировать ]С 1968 года такие ученые, как Виктор Веселаго, размышляли о возможности обратного эффекта Доплера. Размер доплеровского сдвига зависит от показателя преломления среды, через которую проходит волна. Некоторые материалы способны к отрицательному преломлению , что должно привести к доплеровскому сдвигу, который работает в направлении, противоположном обычному доплеровскому сдвигу. [24] Первый эксперимент, обнаруживший этот эффект, был проведен Найджелом Седдоном и Тревором Беарпарком в Бристоле , Великобритания , в 2003 году. [стр. 5] Позже обратный эффект Доплера был обнаружен в некоторых неоднородных материалах и предсказан внутри конуса Вавилова – Черенкова. [25]
См. также
[ редактировать ]Первоисточники
[ редактировать ]- ^ Бюллетень Бая (1845 г.). «Акустические эксперименты на голландской железной дороге, а также периодические комментарии к теории профессора Допплера (на немецком языке)» . Анналы физики и химии . 142 (11): 321–351. Бибкод : 1845АнП...142..321Б . дои : 10.1002/andp.18451421102 .
- ^ Физо: «Акустика и оптика». Лекция, Société Philomathique de Paris , 29 декабря 1848 года. По словам Беккера (стр. 109), она никогда не была опубликована, но рассказана М. Муаньо (1850): «Répertoire d'optique Moderne» (на французском языке), том 3. . стр. 1165–1203, а затем полностью Физо, «О влиянии движения на тон звуковых колебаний и длину волны лучей света»; [Париж, 1870]. Анналы химии и физики , 19, 211–221.
- ^ Скотт Рассел, Джон (1848). «О некоторых эффектах, оказываемых на звук быстрым движением наблюдателя» . Отчет восемнадцатого собрания Британской ассоциации содействия развитию науки . 18 (7): 37–38 . Проверено 8 июля 2008 г.
- ^ Петреску, Флориан Ион Т (2015). «Улучшение медицинской визуализации и измерения кровотока с помощью новой зависимости эффекта Доплера» . Американский журнал инженерных и прикладных наук . 8 (4): 582–588. doi : 10.3844/ajeassp.2015.582.588 – через Proquest.
- ^ Козырев Александр Борисович; ван дер Вейде, Дэниел В. (2005). «Объяснение обратного эффекта Доплера, наблюдаемого в нелинейных линиях передачи». Письма о физических отзывах . 94 (20): 203902. Бибкод : 2005PhRvL..94t3902K . doi : 10.1103/PhysRevLett.94.203902 . ПМИД 16090248 .
Ссылки
[ редактировать ]- ^ Соединенные Штаты. Военно-морское ведомство (1969). «Принципы и применение подводного звука», первоначально выпущенные как краткий технический отчет Отдела 6, NDRC, Vol. 7, 1946 г., перепечатано... 1968 г. п. 194 . Проверено 29 марта 2021 г.
- ^ Джозеф, А. (2013). Измерение океанских течений: инструменты, технологии и данные . Эльзевир Наука. п. 164. ИСБН 978-0-12-391428-6 . Проверено 30 марта 2021 г.
- ^ Перейти обратно: а б Джордано, Николас (2009). Студенческая физика: рассуждения и взаимосвязи . Cengage Обучение. стр. 421–424. ISBN 978-0534424718 .
- ^ Перейти обратно: а б Поссель, Маркус (2017). «Волны, движение и частота: эффект Доплера» . Эйнштейн Онлайн, Том. 5 . Институт гравитационной физики Макса Планка, Потсдам, Германия. Архивировано из оригинала 14 сентября 2017 года . Проверено 4 сентября 2017 г.
- ^ Хендерсон, Том (2017). «Эффект Доплера – Урок 3, Волны» . Учебник по физике . Кабинет физики . Проверено 4 сентября 2017 г.
- ^ Алек Иден В поисках Кристиана Допплера , Springer-Verlag, Вена, 1992. Содержит факсимильное издание с английским переводом.
- ^ Беккер (2011). Барбара Дж. Беккер, Распутывание звездного света: Уильям и Маргарет Хаггинсы и развитие новой астрономии , иллюстрированное издание, Cambridge University Press , 2011; ISBN 110700229X , 9781107002296.
- ^ Перейти обратно: а б Уокер, Джерл; Резник, Роберт ; Холлидей, Дэвид (2007). Основы физики Холлидея и Резника (8-е изд.). Уайли. ISBN 9781118233764 . OCLC 436030602 .
- ^ Стратт (лорд Рэлей), Джон Уильям (1896). Макмиллан и компания (ред.). Теория звука . Том. 2 (2-е изд.). Макмиллан. п. 154.
- ^ «Допплеровский сдвиг» . astro.ucla.edu .
- ^ Харрисон, Эдвард Роберт (2000). Космология: Наука о Вселенной (2-е изд.). Издательство Кембриджского университета. стр. 306 и далее . ISBN 978-0-521-66148-5 .
- ^ Дж. А. Пикок (2008). «Обличительная речь о расширении пространства». arXiv : 0809.4573 [ астроф-ф ].
- ^ Банн, EF; Хогг, Д.В. (2009). «Кинематическое происхождение космологического красного смещения». Американский журнал физики . 77 (8): 688–694. arXiv : 0808.1081 . Бибкод : 2009AmJPh..77..688B . дои : 10.1119/1.3129103 . S2CID 1365918 .
- ^ Отличный обзор темы с техническими деталями дан здесь: Персиваль, Уилл; Самушия, Ладо; Росс, Эшли; Шапиро, Чарльз; Ракканелли, Альвизе (2011). «Обзорная статья: Искажения пространства в области красного смещения» . Философские труды Королевского общества . 369 (1957): 5058–67. Бибкод : 2011RSPTA.369.5058P . дои : 10.1098/rsta.2011.0370 . ПМИД 22084293 .
- ^ Вольф, дипломированный инженер. (ФХ) Кристиан. «Основы радиолокации» . радартуториал.еу . Проверено 14 апреля 2018 г.
- ^ Дэвис, MJ; Ньютон, доктор медицинских наук (2 июля 2017 г.). «Неинвазивная визуализация в кардиологии для врачей общей практики». Британский журнал больничной медицины . 78 (7): 392–398. дои : 10.12968/hmed.2017.78.7.392 . ПМИД 28692375 .
- ^ Аппис, AW; Трейси, MJ; Файнштейн, С.Б. (1 июня 2015 г.). «Обновленная информация о безопасности и эффективности коммерческих ультразвуковых контрастных веществ в кардиологии» . Эхо Исследования и Практика . 2 (2): 55–62 р. дои : 10.1530/ERP-15-0018 . ПМЦ 4676450 . ПМИД 26693339 .
- ^ Эванс, Д.Х.; Макдикен, WN (2000). Допплеровское УЗИ (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-97001-9 . [ нужна страница ]
- ^ Отилия Попескуй, Джейсон С. Харрис и Димитри К. Попескуз, Проектирование подсистемы связи для миссий наноспутников CubeSat: перспективы эксплуатации и реализации, 2016, IEEE
- ^ Цинчун, Лю (1999). «Доплеровское измерение и компенсация в системах мобильной спутниковой связи». MILCOM 1999. Военные коммуникации IEEE. Материалы конференции (кат. № 99CH36341) . Том. 1. С. 316–320. CiteSeerX 10.1.1.674.3987 . дои : 10.1109/milcom.1999.822695 . ISBN 978-0-7803-5538-5 . S2CID 12586746 .
- ^ Оберг, Джеймс (4 октября 2004 г.). «Зов Титана» . IEEE-спектр . Архивировано из оригинала 14 сентября 2012 г. (не в сети по состоянию на 14 октября 2006 г., см. версию Интернет-архива )
- ^ Арндт, Д. (2015). О моделировании каналов для приема наземных мобильных спутников (докторская диссертация).
- ^ Агарвал, Саураб; Гаурав, Ашиш Кумар; Нирала, Мехул Кумар; Синха, Саян (2018). «Звезда RRT на основе потенциала и выборки для динамического планирования движения в реальном времени с учетом импульса в функции стоимости». Нейронная обработка информации . Конспекты лекций по информатике. Том. 11307. стр. 209–221. дои : 10.1007/978-3-030-04239-4_19 . ISBN 978-3-030-04238-7 .
- ^ «Доплеровский сдвиг наблюдается в обратном направлении» . Мир физики . 10 марта 2011 г.
- ^ Ши, Сиханг; Линь, Сяо; Каминер, Идо; Гао, Фэй; Ян, Чжаоцзюй; Джоаннопулос, Джон Д.; Солячич, Марин; Чжан, Бэйле (октябрь 2018 г.). «Сверхлегкий обратный эффект Доплера». Физика природы . 14 (10): 1001–1005. arXiv : 1805.12427 . Бибкод : 2018arXiv180512427S . дои : 10.1038/s41567-018-0209-6 . ISSN 1745-2473 . S2CID 125790662 .
Дальнейшее чтение
[ редактировать ]- Допплер, К. (1842). О цветном свете двойных звезд и некоторых других звезд неба . Издательство: Королевские трактаты. Бём. Труды Королевского богемского общества наук (Часть V, Том 2)]; Прага: 1842 г. (переиздано в 1903 г.). В некоторых источниках в качестве года публикации упоминается 1843 год, поскольку в этом году статья была опубликована в «Трудах Богемского общества наук». Сам Доплер называл публикацию «Прага 1842 года от Борроша и Андре», потому что в 1842 году у него было напечатано предварительное издание, которое он распространял независимо.
- «Допплер и эффект Доплера», EN da C. Andrade, Endeavour Vol. XVIII № 69, январь 1959 г. (опубликовано ICI в Лондоне). Исторический отчет об оригинальной статье Доплера и последующих разработках.
- Дэвид Нолти (2020). Падение и повышение эффекта Доплера. Физика сегодня, т. 73, стр. 31 - 35. DOI: 10.1063/PT.3.4429.
- Адриан, Элени (24 июня 1995 г.). «Эффект Доплера» . НКСА . Архивировано из оригинала 12 мая 2009 года . Проверено 13 июля 2008 г.
Внешние ссылки
[ редактировать ] СМИ, связанные с эффектом Доплера, на Викискладе?
СМИ, связанные с эффектом Доплера, на Викискладе? - Эффект Доплера - Фейнмановские лекции по физике
- Эффект Доплера , ScienceWorld