Лимасон

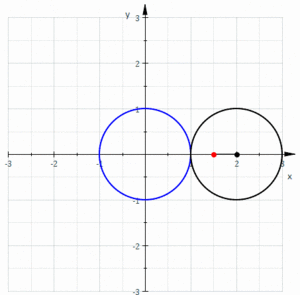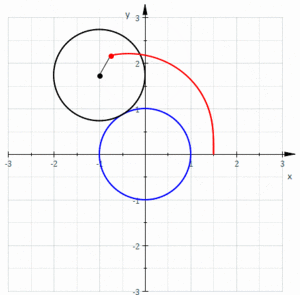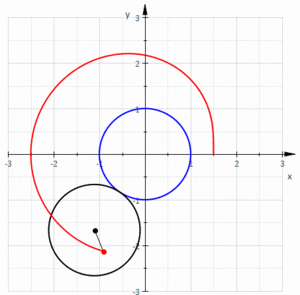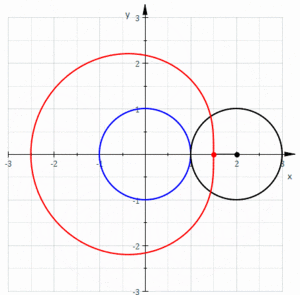
В геометрии лимасон образованная или лимакон / ˈ l ɪ m ə s ɒ n / , также известный как лимасон Паскаля или улитка Паскаля , определяется как кривая рулетки, траекторией точки, прикрепленной к кругу , когда этот круг катится. вокруг внешней стороны круга равного радиуса. Ее также можно определить как рулетку, образующуюся, когда круг катится по кругу с половиной его радиуса так, что меньший круг оказывается внутри большего круга. Таким образом, они принадлежат к семейству кривых, называемых центрированными трохоидами ; более конкретно, они являются эпитрохоидами . Кардиоида — это особый случай , в котором точка, образующая рулетку, лежит на катящемся круге; результирующая кривая имеет точку возврата .

В зависимости от положения точки, образующей кривую, она может иметь внутреннюю и внешнюю петли (что дает семейству название), может иметь форму сердца или овала.

Лимасон — это бициркулярная рациональная плоская алгебраическая кривая степени 4 .

Три лимасона: с ямочками, с острием ( кардиоида ) и петлеобразным. Не показано: выпуклый Лимасон.

История

Самое раннее официальное исследование лимасонов обычно приписывают Этьену Паскалю , отцу Блеза Паскаля . Однако некоторые глубокие исследования относительно них были предприняты ранее немецким эпохи Возрождения художником Альбрехтом Дюрером . «Underweysung der Messung» Дюрера («Инструкция по измерению») содержит конкретные геометрические методы изготовления лимасонов. Кривая была названа Жилем де Робервалем, когда он использовал ее в качестве примера для поиска касательных линий.

Уравнения

Уравнение (с точностью до переноса и вращения) лимасона в полярных координатах имеет вид

r=b+a\cos \theta .

Их можно преобразовать в декартовы координаты , умножив на r (таким образом введя точку в начале координат, которая в некоторых случаях является ложной) и заменив $r^{2}=x^{2}+y^{2}$ и $r\cos \theta =x$ чтобы получить ^[1]

\left(x^{2}+y^{2}-ax\right)^{2}=b^{2}\left(x^{2}+y^{2}\right).

Применяя параметрическую форму полярного преобразования в декартову систему, мы также имеем ^[2]

x=(b+a\cos \theta )\cos \theta ={a \over 2}+b\cos \theta +{a \over 2}\cos 2\theta ,

y=(b+a\cos \theta )\sin \theta =b\sin \theta +{a \over 2}\sin 2\theta ;

при настройке

z=x+iy=(b+a\cos \theta )(\cos \theta +i\sin \theta )

дает эту параметризацию в виде кривой на комплексной плоскости :

z={a \over 2}+be^{i\theta }+{a \over 2}e^{2i\theta }.

Если бы мы сместились по горизонтали на ${\textstyle -{\frac {1}{2}}a}$ , то есть,

z=be^{it}+{a \over 2}e^{2it}

,

мы бы, изменив положение начала координат, перешли бы к обычной форме уравнения центрированной трохоиды. Обратите внимание на изменение независимой переменной в этот момент, чтобы было ясно, что мы больше не используем параметризацию полярных координат по умолчанию. $\theta =\arg z$ .

Особые случаи

В особом случае $a=b$ , полярное уравнение

r=b(1+\cos \theta )=2b\cos ^{2}{\frac {\theta }{2}}

или

r^{1 \over 2}=(2b)^{1 \over 2}\cos {\frac {\theta }{2}},

что делает его членом семейства синусоидальных спиральных кривых. Эта кривая является кардиоидой .

В особом случае $a=2b$ , центрированная трохоидная форма уравнения принимает вид

z=b\left(e^{it}+e^{2it}\right)=be^{3it \over 2}\left(e^{it \over 2}+e^{-it \over 2}\right)=2be^{3it \over 2}\cos {t \over 2},

или, в полярных координатах,

r=2b\cos {\theta  \over 3}

что делает его членом семейства кривых роз . Эта кривая представляет собой трисектрису и иногда называется трисектрисой Лимасона .

Форма

Когда $b>a$ , Лимасон представляет собой простую замкнутую кривую. Однако начало координат удовлетворяет декартову уравнению, приведенному выше, поэтому график этого уравнения имеет акнод или изолированную точку.

Когда $b>2a$ , то область, ограниченная кривой, выпуклая, а когда $a<b<2a$ кривая имеет углубление, ограниченное двумя точками перегиба . В $b=2a$ , точка $(-a,0)$ это точка кривизны 0 .

Как $b$ снижается по отношению к $a$ , отступ становится более выраженным до тех пор, пока при $b=a$ , кривая становится кардиоидой, а углубление становится точкой возврата . Для $0<b<a$ , точка возврата расширяется до внутренней петли, и кривая пересекает себя в начале координат. Как $b$ приближается к 0, петля заполняет внешнюю кривую и, в пределе, лимасон становится кругом, пройденным дважды.

Измерение

Территория, окруженная Лимасоном $r=b+a\cos \theta$ является ${\textstyle \left(b^{2}+{{a^{2}} \over 2}\right)\pi }$ . Когда $b<a$ при этом площадь, заключенная во внутренний цикл, учитывается дважды. В этом случае кривая пересекает начало координат под углами ${\textstyle \pi \pm \arccos {b \over a}}$ , площадь, заключенная во внутренний цикл, равна

\left(b^{2}+{{a^{2}} \over 2}\right)\arccos {b \over a}-{3 \over 2}b{\sqrt {a^{2}-b^{2}}},

площадь, заключенная во внешний цикл, равна

\left(b^{2}+{{a^{2}} \over 2}\right)\left(\pi -\arccos {b \over a}\right)+{3 \over 2}b{\sqrt {a^{2}-b^{2}}},

а площадь между петлями равна

\left(b^{2}+{{a^{2}} \over 2}\right)\left(\pi -2\arccos {b \over a}\right)+3b{\sqrt {a^{2}-b^{2}}}.

^[1]

Длина окружности лимасона определяется полным эллиптическим интегралом второго рода :

4(a+b)E\left({{2{\sqrt {ab}}} \over a+b}\right).

Связь с другими кривыми

Позволять $P$ быть точкой и $C$ быть кругом, центр которого не $P$ . Тогда огибающая тех кругов, центр которых лежит на $C$ и это проходит $P$ это лимасон.

Педаль . круга – лимасон Фактически педаль относительно начала окружности радиусом $b$ и центр $(a,0)$ имеет полярное уравнение $r=b+a\cos \theta$ .

Обратное относительно единичного круга $r=b+a\cos \theta$ является

r={1 \over {b+a\cos \theta }}

которое представляет собой уравнение конического сечения с эксцентриситетом

{\tfrac {a}{b}}

и сосредоточьтесь на начале координат. Таким образом, лимасон можно определить как обратную конику, где центр инверсии является одним из фокусов. Если коника — парабола, то обратная коника будет кардиоидой, если коника — гипербола, то соответствующий лимасон будет иметь внутреннюю петлю, а если коника — эллипс, то соответствующий лимасон не будет иметь петли.

Раковина окружности относительно точки на окружности является лимасоном.

Частным частным случаем декартова овала является лимасон. ^[3]

См. также

Ссылки

^ Jump up to: Перейти обратно: ^а ^б Дж. Деннис Лоуренс (1972). Каталог специальных плоских кривых . Дуврские публикации. стр. 113–118 . ISBN 0-486-60288-5 .
^ Вайсштейн, Эрик В. «Лимасон». Из MathWorld — веб-ресурса Wolfram.
^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Декартовский овал» , Архив истории математики MacTutor , Университет Сент-Эндрюс

Дальнейшее чтение

Джейн Гроссман и Майкл Гроссман. «Ямочка или нет ямочки» , Двухлетний математический журнал колледжа , январь 1982 г., страницы 52–55.
Говард Антон. Исчисление , 2-е издание, стр. 708, John Wiley & Sons, 1984.
Говард Антон. [1] стр. 725 – 726.
Говард Ивс. Обзор геометрии , том 2 (страницы 51,56,273), Аллин и Бэкон, 1965.

Внешние ссылки

[Lawrence-1] Jump up to: Перейти обратно: ^а ^б Дж. Деннис Лоуренс (1972). Каталог специальных плоских кривых . Дуврские публикации. стр. 113–118 . ISBN 0-486-60288-5 .

[Weisstein-2] Вайсштейн, Эрик В. «Лимасон». Из MathWorld — веб-ресурса Wolfram.

[3] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Декартовский овал» , Архив истории математики MacTutor , Университет Сент-Эндрюс

[1]

[2]

[3]