Нулевой вектор

Эта статья о нулях квадратичной формы. Чтобы узнать о нулевом элементе в векторном пространстве, см. Нулевой вектор . Для нулевых векторов в пространстве Минковского см. Пространство Минковского § Причинная структура .

Нулевой конус, где $q(x,y,z)=x^{2}+y^{2}-z^{2}.$

В математике , если задано векторное пространство X с ассоциированной квадратичной формой q , записанной ( X , q ) , нулевой вектор или изотропный вектор — это ненулевой элемент x из X , для которого q ( x ) = 0 .

В теории действительных билинейных форм различают квадратичные формы и изотропные квадратичные формы определенные . Они отличаются тем, что только для последнего существует ненулевой нулевой вектор.

Квадратичное пространство ( X , q ), имеющее нулевой вектор, называется псевдоевклидовым пространством . Термин изотропный вектор v , когда q ( v ) = 0, использовался в квадратичных пространствах, и анизотропное пространство для квадратичного пространства без нулевых векторов.

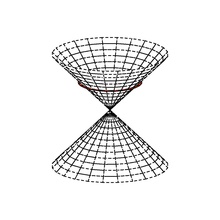
Псевдоевклидово векторное пространство может быть разложено (неоднозначно) на подпространства A и B , X = A + B , где q положительно определенное на A и отрицательно определенное на B. ортогональные Нулевой конус или изотропный конус X состоит из объединения сбалансированных сфер: $$\bigcup _{r\geq 0}\{x=a+b:q(a)=-q(b)=r,\ \ a\in A,\ \ b\in B\}.$$ Нулевой конус также представляет собой объединение изотропных линий, проходящих через начало координат.

Сплит-алгебры

Композиционная алгебра с нулевым вектором является расщепляемой алгеброй .

В композиционной алгебре ( A , +, ×, *) квадратичная форма равна q( x ) = xx *. Когда x не существует мультипликативного обратного вектора — нулевой вектор, то для x , и поскольку x ≠ 0, A не является алгеброй с делением .

В конструкции Кэли-Диксона расщепляемые алгебры возникают в рядах бикомплексных чисел , бикватернионов и биоктонионов , которые используют комплексных чисел поле $\mathbb {C}$ как основу этой удвоенной конструкции принадлежит Л. Е. Диксону (1919). В частности, эти алгебры имеют две мнимые единицы , которые коммутируют так, что их произведение в квадрате дает +1:

$(hi)^{2}=h^{2}i^{2}=(-1)(-1)=+1.$ Затем

$(1+hi)(1+hi)^{*}=(1+hi)(1-hi)=1-(hi)^{2}=0$ поэтому 1 + hi — нулевой вектор.

Настоящие подалгебры, расщепленные комплексные числа , разделенные кватернионы и разделенные октонионы с их нулевыми конусами, представляющими движение света в 0 ∈ A и из него , предполагают топологию пространства-времени .

Примеры

Светоподобные векторы пространства Минковского являются нулевыми векторами.

Четыре линейно независимых бикватерниона l = 1 + hi , n = 1 + hj , m = 1 + hk и m ^∗ = 1 – hk – нулевые векторы и { l , n , m , m ^∗ } может служить основой для подпространства, используемого для представления пространства-времени . Нулевые векторы также используются в подходе формализма Ньюмана-Пенроуза к пространственно-временным многообразиям.

В модуле Верма алгебры Ли имеются нулевые векторы.

Ссылки

• Дубровин, Б.А.; Фоменко А.Т. ; Новиков, СП (1984). Современная геометрия: методы и приложения . Перевод Бернса, Роберта Г. Спрингера. п. 50 . ISBN  0-387-90872-2 .
• Шоу, Рональд (1982). Линейная алгебра и представления групп . Том. 1. Академическая пресса . п. 151. ИСБН  0-12-639201-3 .
• Невилл, Э.Х. (Эрик Гарольд) (1922). Пролегомены к аналитической геометрии в анизотропном евклидовом пространстве трех измерений . Издательство Кембриджского университета . п. 204 .