Принцип локальности

Эта статья о принципе локальности в физике. Чтобы узнать о других значениях, см. «Местоположение» .

В физике принцип локальности гласит, что на объект непосредственно влияет только его непосредственное окружение. Теория, включающая принцип локальности, называется «локальной теорией». Это альтернатива концепции мгновенного, или «нелокального» действия на расстоянии . Локальность возникла из полевых теорий классической физики . Идея состоит в том, что для того, чтобы причина в одной точке имела следствие в другой точке, что-то в пространстве между этими точками должно опосредовать действие. Чтобы оказать влияние, что-то, например волна или частица, должно пройти через пространство между двумя точками, неся влияние.

Специальная теория относительности ограничивает максимальную скорость, с которой может распространяться причинное влияние, до скорости света . $c$. Следовательно, принцип локальности подразумевает, что событие в одной точке не может вызвать действительно одновременный результат в другой точке. Событие в точку $A$ не может вызвать результат в точке $B$ за время меньше, чем $T=D/c$, где $D$ расстояние между точками и $c$ это скорость света в вакууме.

Принцип локальности играет решающую роль в одном из центральных результатов квантовой механики. В 1935 году Альберт Эйнштейн , Борис Подольский и Натан Розен в своем мысленном эксперименте с парадоксом ЭПР выдвинули гипотезу о том, что квантовая механика не может быть полной теорией. Они описали две системы, физически разделенные после взаимодействия; эту пару можно было бы назвать запутанной в современной терминологии . Они полагали, что без дополнений, которые теперь называются скрытыми переменными , квантовая механика предсказывает нелогичные отношения между физически разделенными измерениями.

В 1964 году Джон Стюарт Белл сформулировал теорему Белла — неравенство, нарушение которого в реальных экспериментах означает, что квантовая механика нарушает локальную причинность (в более поздних работах называемую локальным реализмом ), результат, который теперь считается эквивалентным исключению локальных скрытых переменных . Прогрессивные вариации этих тестовых экспериментов Белла с тех пор показали, что квантовая механика в целом нарушает неравенства Белла. Согласно некоторым интерпретациям квантовой механики , этот результат подразумевает, что некоторые квантовые эффекты нарушают принцип локальности.

Доквантовая механика

Основная статья: Действия на расстоянии

Ньютона В 17 веке принцип всемирного тяготения был сформулирован в терминах «действия на расстоянии», тем самым нарушив принцип локальности. Сам Ньютон считал это нарушение абсурдным:

Немыслимо, чтобы неодушевленная Материя могла без посредничества чего-то еще, что не является материальным, воздействовать на другую материю и воздействовать на нее без взаимного Контакта… Эта Гравитация должна быть врожденной, присущей и существенной для Материи, чтобы одно тело могло воздействовать на нее. другое, на расстоянии, через вакуум, без посредничества чего-либо еще, с помощью которого их действие и сила могут передаваться от одного к другому, является для меня настолько абсурдным, что я не верю ни одному человеку, который имел бы в философских вопросах компетентная способность мышления всегда может в него впасть. Гравитация должна быть вызвана Агентом, действующим постоянно по определенным законам; но будет ли этот агент материальным или нематериальным, я предоставил на рассмотрение моих читателей.

- Исаак Ньютон, Письма к Бентли , 1692/3.

Закон электрических сил Кулона первоначально также был сформулирован как мгновенное действие на расстоянии, но в 1880 году Джеймс Клерк Максвелл показал, что уравнения поля , подчиняющиеся локальности, предсказывают все явления электромагнетизма. Эти уравнения показывают, что электромагнитные силы распространяются со скоростью света.

В 1905 году Альберта Эйнштейна постулировала специальная теория относительности , что никакая материя и энергия не могут двигаться быстрее скорости света, и тем самым Эйнштейн стремился переформулировать физику таким образом, чтобы она подчинялась принципу локальности. Позже ему удалось создать альтернативную теорию гравитации — общую теорию относительности , которая подчиняется принципу локальности.

породила другой вызов принципу локальности Однако впоследствии теория квантовой механики , которую помог создать сам Эйнштейн, .

Модели для местности

Диаграмма локальности в квантовой механике

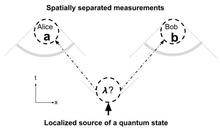
Простые пространственно-временные диаграммы могут помочь прояснить вопросы, связанные с локальностью. Способ описания вопросов локальности, подходящий для обсуждения квантовой механики , показан на диаграмме. Частица создается в одном месте, затем разделяется и измеряется в двух других, пространственно разделенных местах. Эти два измерения названы в честь Алисы и Боба. Алиса выполняет измерения (А) и получает результат $\mathbf {a}$); Боб выступает ( $B$) и получает результат $\mathbf {b}$. Эксперимент повторяют много раз и сравнивают результаты.

Алиса и Боб в пространстве-времени

Алиса и Боб на диаграмме пространства-времени

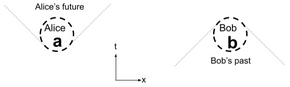
На пространственно-временной диаграмме временная координата идет вертикально, а пространственная координата — горизонтально. Алиса в локальном регионе слева может влиять на события только в конусе, простирающемся в будущее, как показано; конечная скорость света не позволяет ей влиять на другие области, включая местоположение Боба в данном случае. Точно так же мы можем использовать диаграмму, чтобы понять, что локальные обстоятельства Боба не могут быть изменены Алисой одновременно: все события, которые влияют на Боба, находятся в конусе под его местоположением на диаграмме. Пунктирные линии вокруг Алисы показывают ее действительные будущие местоположения; пунктирные линии вокруг Боба показывают события, которые могли стать причиной его нынешней ситуации. Когда Алиса измеряет квантовые состояния в своем местоположении, она получает результаты, помеченные как $\mathbf {a}$; аналогично Боб получает $\mathbf {b}$. Модели местности пытаются объяснить статистическую взаимосвязь между этими измеренными значениями.

Действие на расстоянии

Действие на расстоянии

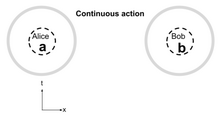
Простейшая модель локальности — это отсутствие локальности: мгновенное действие на расстоянии без ограничений относительности. Модель локальности для действия на расстоянии называется непрерывным действием . Серая зона (здесь кружок) — это математическое понятие, называемое «экраном». Любой путь из локации через экран становится частью физической модели в этой локации. Серое кольцо указывает на то, что события из всех частей пространства и времени могут повлиять на вероятность, измеренную Алисой или Бобом. Таким образом, в случае непрерывного действия события в любое время и в любом месте влияют на модель Алисы и Боба. Эта простая модель очень успешна для солнечно-планетарной динамики с ньютоновской гравитацией и в электростатике, когда релятивистские эффекты незначительны.

Нет зависимости от будущих вводимых данных

Нет зависимости от будущих вводимых данных

Многие модели местности явно или неявно игнорируют возможный эффект будущих событий. Диаграмма пространства-времени справа показывает эффект такого ограничения в сочетании с непрерывным действием. Входные данные из будущего (над пунктирной линией) больше не считаются частью модели Алисы или Боба. Сравнение этой диаграммы с диаграммой непрерывного действия показывает, что это не одна и та же модель локальности. Аргументы здравого смысла о том, что будущее не влияет на настоящее, являются разумными критериями, но такие предположения изменяют математический характер моделей.

Локальная причинность Белла

Локальная причинность Белла

Джон Стюарт Белл при обсуждении своей теоремы Белла использует модель скрининга, показанную справа. События из общего прошлого Алисы и Боба являются частью модели, используемой при вычислении вероятностей для Алисы и Боба, что указывает на то, как экран воспринимает эти события. Однако события в местоположении Боба во время измерения Алисы и события в будущем исключаются. Белл назвал это предположение локальной причинностью , но с помощью диаграммы мы можем рассуждать о значении предположения, не запутываясь в других значениях локального в сочетании с другими значениями причинного. Пунктирные линии показывают релятивистски достоверные регионы в прошлом Алисы или Боба. Серая дуга — это предполагаемый «экран» Белла.

Квантовая механика

Относительное положение наших немногочисленных, легко различимых планет (например) можно увидеть непосредственно: понимание и измерение их относительного положения ставит лишь технические вопросы. С другой стороны, субмикроскопический мир познается только посредством измерений, которые усредняются по многим, казалось бы, случайным («статистическим» или «вероятностным») событиям, и измерения могут давать результаты либо корпускулярные, либо волновые, в зависимости от их конструкции. Этим миром управляет квантовая механика . Понятия локальности более сложны и описываются на языке вероятности и корреляции .

В статье о парадоксе Эйнштейна-Подольского-Розена 1935 года (статья EPR) Альберт Эйнштейн , Борис Подольский и Натан Розен придумали такой эксперимент. Они заметили, что квантовая механика предсказывает то, что сейчас известно как квантовая запутанность , и исследовали ее последствия. По их мнению, классический принцип локальности подразумевал, что «никаких реальных изменений не может произойти» на участке Боба в результате любых измерений, которые проводила Алиса. Поскольку квантовая механика предсказывает коллапс волновой функции, который зависит от выбора Бобом меры измерения, они пришли к выводу, что это форма действия на расстоянии и что волновая функция не может быть полным описанием реальности. Другие физики не согласились: они признали квантовую волновую функцию полной и поставили под сомнение природу локальности и реальности, предполагаемую в статье ЭПР.

В 1964 году Джон Стюарт Белл исследовал, возможно ли достичь цели Эйнштейна — «завершить» квантовую теорию — с помощью локальных скрытых переменных , чтобы объяснить корреляции между пространственно разделенными частицами, как предсказывает квантовая теория. Белл установил критерий, позволяющий различать теорию локальных скрытых переменных и квантовую теорию, измеряя конкретные значения корреляций между запутанными частицами. Последующие экспериментальные испытания показали, что некоторые квантовые эффекты действительно нарушают неравенства Белла и не могут быть воспроизведены с помощью теории локальных скрытых переменных. Теорема Белла зависит от тщательно определенных моделей локальности.

Локальность и скрытые переменные

Основная статья: теорема Белла

Белл описал локальную причинность с точки зрения вероятности, необходимой для анализа квантовой механики. Используя обозначения, что $P(\mathbf {r} |g)$ на вероятность результата $\mathbf {r}$ с данным состоянием $g$Белл исследовал распределение вероятностей $$P(\mathbf {ab} |AB,\lambda )$$где $\lambda$ представляет скрытый набор переменных состояния (локально), когда две частицы изначально расположены рядом. Если локальная причинность верна, то вероятности, наблюдаемые Алисой и Бобом, должны быть связаны только скрытыми переменными, и мы можем показать, что $$P(\mathbf {ab} |AB,\lambda )=P(\mathbf {a} |A,\lambda )P(\mathbf {b} |B,\lambda ),$$ Белл доказал, что следствием этой факторизации являются ограничения на корреляции, наблюдаемые Алисой и Бобом, известные как неравенства Белла. Поскольку квантовая механика предсказывает корреляции, более сильные, чем этот предел, локально установленные скрытые переменные не могут быть добавлены к «полной» квантовой теории, как того требует статья ЭПР.

Многочисленные эксперименты, специально предназначенные для исследования проблем локальности, подтверждают предсказания квантовой механики; к ним относятся эксперименты, в которых два места измерения находятся на расстоянии более километра друг от друга. 2022 года Нобелевская премия по физике была присуждена Алену Аспекту , Джону Клаузеру и Антону Цайлингеру , в частности, «за эксперименты со запутанными фотонами, устанавливающие нарушение неравенств Белла». Конкретный аспект квантовой теории, который приводит к этим корреляциям, называется квантовой запутанностью , и версии сценария Белла теперь используются для экспериментальной проверки запутанности.

Терминология

Основная статья: Квантовая нелокальность

См. Также: Теорема Белла § Интерпретации.

Математические результаты Белла по сравнению с экспериментальными данными исключают локальные математические квантовые теории скрытых переменных. Но интерпретация математики по отношению к физическому миру остается предметом дискуссий. Белл описал предположения, лежащие в основе его работы, как «локальную причинность», сокращенно «локальность»; более поздние авторы называли эти предположения локальным реализмом . Эти разные названия не меняют математических предположений.

Обзор документов Использование этой фразы предполагает, что общее (классическое) физическое определение реализма таково:

предположение, что результаты измерений четко определены заранееи независимо от измерений.

Это определение включает в себя классические понятия, такие как «четко определенное», которое противоречит квантовой суперпозиции , и «до… измерений», которое подразумевает (метафизическое) предсуществование свойств. В частности, термин локальный реализм в контексте теоремы Белла не может рассматриваться как своего рода «реализм», включающий в себя иную локальность, чем та, которая подразумевается в предположении экранирования Белла. Этот конфликт между общими идеями реализма и квантовой механики требует тщательного анализа всякий раз, когда обсуждается локальный реализм. Добавление модификатора «локальности», означающего, что результаты двух пространственно хорошо разделенных измерений не могут причинно влиять друг на друга, не делает комбинацию связанной с доказательством Белла; единственная интерпретация, которую принял Белл, была та, которую он назвал локальной причинностью. Следовательно, теорема Белла не ограничивает возможности нелокальных переменных, а также теорий, основанных на ретропричинности или супердетерминизме .

Из-за вероятностного характера коллапса волновой функции это очевидное нарушение локальности в квантовой механике не может использоваться для передачи информации быстрее, чем свет, в соответствии с теоремой об отсутствии связи . Ашер Перес различает слабую и сильную нелокальность , причем последняя относится к теориям, позволяющим осуществлять связь со скоростью, превышающей скорость света. В этих условиях квантовая механика допускала бы слабо нелокальные корреляции, но не допускала бы сильную нелокальность.

Релятивистская квантовая механика

Одним из основных принципов квантовой теории поля является принцип локальности. Операторы поля и плотность Лагранжа, описывающие динамику полей, являются локальными в том смысле, что взаимодействия не описываются действием на расстоянии. Этого можно достичь, избегая членов лагранжиана, которые являются произведениями двух полей, зависящих от удаленных координат. В частности, в релятивистской квантовой теории поля для обеспечения соблюдения принципов локальности и причинности требуется следующее условие: если есть две наблюдаемые , каждая из которых локализована в двух различных областях пространства-времени, которые оказываются на пространственноподобном расстоянии друг от друга, наблюдаемые должны добираться . Это условие иногда навязывают как одну из аксиом релятивистской квантовой теории поля.

См. также

• Мысленные эксперименты Эйнштейна
• Локальная теория скрытых переменных
• Нелокальность (значения)
• Квантовая нелокальность
• Декомпозиция кластера
• Контрфактическая определенность

Внешние ссылки

• Квантовая нелокальность против эйнштейновской локальности Х. Дитера Це