Коническое пересечение
В квантовой химии коническое пересечение двух или более поверхностей потенциальной энергии представляет собой набор точек молекулярной геометрии , в которых поверхности потенциальной энергии вырождены (пересекаются), а неадиабатические связи между этими состояниями не исчезают. Вблизи конических пересечений приближение Борна-Оппенгеймера нарушается, и связь между движением электрона и ядра становится важной, позволяя иметь место неадиабатическим процессам. Таким образом, расположение и характеристика конических пересечений необходимы для понимания широкого спектра важных явлений, управляемых неадиабатическими событиями, таких как фотоизомеризация, фотосинтез, зрение и фотостабильность ДНК. Коническое пересечение, включающее поверхность потенциальной энергии основного электронного состояния C 6 H 3 F 3 + Молекулярный ион обсуждается в связи с эффектом Яна-Теллера в разделе 13.4.2 на страницах 380-388 учебника Банкера и Йенсена. [1]
Конические пересечения также называют молекулярными воронками или дьявольскими точками , поскольку они стали общепринятой парадигмой для понимания механизмов реакций в фотохимии, столь же важных, как и переходные состояния в термохимии. Это обусловлено очень важной ролью, которую они играют в безызлучательных переходах девозбуждения из возбужденных электронных состояний в основное электронное состояние молекул. [2] Например, стабильность ДНК по отношению к УФ -облучению обусловлена таким коническим пересечением. [3] Пакет молекулярных волн в некоторое электронное возбужденное состояние фотоном , возбужденный УФ- , следует наклону поверхности потенциальной энергии и достигает конического пересечения сверху. В этот момент очень сильная вибронная связь вызывает безызлучательный переход (прыжок по поверхности), который возвращает молекулу в ее основное электронное состояние . Особенность вибронной связи на конических пересечениях ответственна за существование геометрической фазы , открытой Лонге-Хиггинсом. [4] в этом контексте.
Вырожденные точки между поверхностями потенциальной энергии лежат в так называемом пространстве пересечения или шва с размерностью 3N-8 (где N — число атомов). Любые критические точки в этом пространстве вырождения характеризуются как минимумы, переходные состояния или седловые точки более высокого порядка и могут быть связаны друг с другом через аналог собственной координаты реакции в шве. В бензоле, например, существует повторяющаяся структура связности, при которой перестановочно-изомерные сегменты швов соединяются пересечениями точечной группы с более высокой симметрией. [5] Остальные два измерения, которые снимают энергетическое вырождение системы, известны как пространство ветвления.
Экспериментальное наблюдение
[ редактировать ]Чтобы иметь возможность наблюдать это, процесс необходимо замедлить с фемтосекунд до миллисекунд. Новый квантовый эксперимент 2023 года с использованием квантового компьютера с захваченными ионами замедлил интерференционную картину одного атома (вызванную коническим пересечением) в 100 миллиардов раз, что сделало возможным прямое наблюдение. [6]
Локальная характеристика
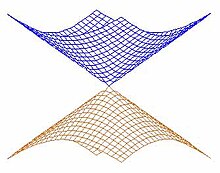
[ редактировать ]Конические пересечения повсеместно встречаются как в тривиальных, так и в нетривиальных химических системах. В идеальной двумерной системе это может произойти при одной молекулярной геометрии . Если поверхности потенциальной энергии изображены как функции двух координат, они образуют конус с центром в точке вырождения. Это показано на соседнем рисунке, где верхняя и нижняя поверхности потенциальной энергии показаны разными цветами. Название «коническое пересечение» происходит от этого наблюдения.
В двухатомных молекулах число колебательных степеней свободы равно 1. Без необходимых двух измерений, необходимых для образования формы конуса, конические пересечения не могут существовать в этих молекулах. Вместо этого кривые потенциальной энергии избегают пересечений , если они имеют одинаковую симметрию точечной группы, в противном случае они могут пересекаться.
В молекулах с тремя и более атомами число степеней свободы молекулярных колебаний не менее 3. В этих системах, когда игнорируется спин-орбитальное взаимодействие , вырождение конического пересечения снимается до первого порядка за счет смещений в двумерном пространстве. подпространство ядерного координатного пространства.
Двумерное подпространство снятия вырождения называется пространством ветвления или плоскостью ветвления . Это пространство натянуто двумя векторами: разницей векторов градиента энергии двух пересекающихся электронных состояний ( вектор g ) и вектором неадиабатической связи между этими двумя состояниями ( вектор h ). Поскольку электронные состояния вырождены, волновые функции двух электронных состояний подвержены произвольному вращению . Следовательно, векторы g и h также подвержены соответствующему произвольному вращению, несмотря на то, что пространство, охватываемое этими двумя векторами, инвариантно. набор волновых функций, который делает векторы g и h Чтобы обеспечить непротиворечивое представление пространства ветвления, обычно выбирается ортогональными. Этот выбор уникален с точки зрения знаков и переключений двух векторов и позволяет этим двум векторам иметь правильную симметрию, когда геометрия молекулы симметрична.
Вырождение сохраняется до первого порядка за счет дифференциальных смещений, перпендикулярных ветвящемуся пространству. Пространство невырожденно-подъемных смещений, являющееся ортогональным дополнением пространства ветвления, называется пространством шва . Движение внутри пространства шва приведет молекулу из одной точки конического пересечения в соседнюю точку конического пересечения. Пространство вырождения, соединяющее различные конические пересечения, можно исследовать и охарактеризовать с помощью методов зонной и молекулярной динамики. [7]
Для молекулы с открытой оболочкой , когда к молекуле добавляется спин-орбитальное взаимодействие, [ нужны разъяснения ] уменьшается размерность шовного пространства. [8]
Наличие конических пересечений можно обнаружить экспериментально. [9] Было предложено использовать двумерную спектроскопию для обнаружения их присутствия посредством модуляции частоты моды колебательной связи. [10] Предложена более прямая спектроскопия конических пересечений, основанная на сверхбыстрой рентгеновской спектроскопии нестационарного поглощения, предлагающая новые подходы к их изучению. [11]
Классификация по симметрии пересекающихся электронных состояний
[ редактировать ]Конические пересечения могут возникать между электронными состояниями с одинаковой или разной симметрией точечной группы, с одинаковой или разной спиновой симметрией. Если ограничиться нерелятивистским кулоновским гамильтонианом, конические пересечения можно классифицировать как требуемые симметрией, случайные разрешенные симметрии или случайные одинаковые симметрии в зависимости от симметрии пересекающихся состояний.
коническое Требуемое симметрией пересечение — это пересечение двух электронных состояний, несущих одно и то же многомерное неприводимое представление. Например, пересечения между парой состояний E в геометрии, имеющей неабелеву групповую симметрию (например, C 3h , C 3v или D 3h ). Его называют обязательным для симметрии, потому что эти электронные состояния всегда будут вырожденными, пока присутствует симметрия. Пересечения, необходимые для симметрии, часто связаны с эффектом Яна – Теллера .
Случайное коническое пересечение , разрешенное симметрией, — это пересечение двух электронных состояний, которые несут разную симметрию точечной группы. Оно называется случайным, потому что состояния могут быть или не быть вырожденными при наличии симметрии. Движение по одному из измерений, вдоль которого снимается вырождение, направление разности градиентов энергии двух электронных состояний, сохранит симметрию, в то время как смещения по другому измерению снятия вырождения, направлению неадиабатических связей, нарушит симметрию молекулы. Таким образом, обеспечивая симметрию молекулы, предотвращается эффект подъема вырождения, вызванный межсостоятельными связями. Таким образом, поиск разрешенного по симметрии пересечения становится одномерной задачей и не требует знания неадиабатических связей, что значительно упрощает задачу. В результате все конические пересечения, обнаруженные с помощью квантово-механических расчетов в первые годы квантовой химии, были пересечениями, разрешенными симметрией.
Случайное коническое пересечение одинаковой симметрии — это пересечение двух электронных состояний, имеющих одинаковую симметрию точечной группы. Хотя этот тип пересечения традиционно было труднее обнаружить, за последнее десятилетие появился ряд эффективных алгоритмов поиска и методов расчета неадиабатических связей. Теперь понятно, что пересечения одинаковой симметрии играют такую же важную роль в неадиабатических процессах, как и пересечения, разрешенные симметрией.
См. также
[ редактировать ]- Яркони, Дэвид (1996). «Дьявольские конические пересечения». Обзоры современной физики . 68 (4): 985–1013. Бибкод : 1996РвМП...68..985Y . дои : 10.1103/RevModPhys.68.985 .
- Баер, Майкл (2006). За пределами Борна – Оппенгеймера: условия электронного неадиабатического взаимодействия и конические пересечения . Уайли-Интерсайенс. дои : 10.1002/0471780081 . ISBN 978-0-471-77891-2 .
- Домке, Вольфганг; Яркони, Дэвид Р.; Кеппель, Хорст (2004). Конические пересечения: электронная структура, динамика и спектроскопия . Продвинутая серия по физической химии. Том. 15. Всемирная научная. дои : 10.1142/5406 . ISBN 978-981-256-546-4 .
- Домке, Вольфганг; Яркони, Дэвид Р.; Кеппель, Хорст (2011). Конические пересечения: теория, расчет и эксперимент . Продвинутая серия по физической химии. Том. 17. Всемирная научная. дои : 10.1142/7803 . ISBN 978-981-4313-45-2 .
- Приближение Борна – Оппенгеймера
- Потенциальная энергетическая поверхность
- Геометрическая фаза
- Кристофер Лонге-Хиггинс
- Диабатическое представительство
- Эффект Яна – Теллера
- Избегали пересечения
- Смягчение связи
- Упрочнение связки
- Вибронная муфта
- Прыжок по поверхности
- Многократный нерест Ab initio
Ссылки
[ редактировать ]- ^ Молекулярная симметрия и спектроскопия , 2-е изд. Филип Р. Банкер и Пер Дженсен, NRC Research Press, Оттава (1998) [1] ISBN 9780660196282
- ^ Тодд Дж. Мартинес (сентябрь 2010 г.). «Физическая химия: Сшивать значит верить» . Природа . 467 (7314): 412–413. Бибкод : 2010Natur.467..412M . дои : 10.1038/467412а . ПМИД 20864993 . S2CID 205058988 .
- ^ Кан, Хёк; Кан Тэк Ли; Бойонг Юнг; Ён Джэ Ко; Сон Гын Ким (октябрь 2002 г.). «Внутреннее время жизни возбужденного состояния оснований ДНК и РНК». Дж. Ам. хим. Соц . 124 (44): 12958–12959. дои : 10.1021/ja027627x . ПМИД 12405817 .
- ^ ХК Лонге Хиггинс; У. Эпик; МХЛ Прайс; Р. А. Зак (1958). «Исследование эффекта Яна-Теллера.II. Динамическая проблема». Учеб. Р. Сок. А. 244 (1236): 1–16. Бибкод : 1958RSPSA.244....1L . дои : 10.1098/rspa.1958.0022 . S2CID 97141844 . См. стр. 12.
- ^ Луис Бланкафорт (ноябрь 2010 г.). «Глобальная картина конического шва пересечения бензола S1/S0» (PDF) . Химическая физика . 377 (1): 60–65. Бибкод : 2010CP....377...60L . doi : 10.1016/j.chemphys.2010.08.016 . hdl : 10044/1/10099 .
- ^ CH Валаху, ВК Олайя-Агудело, Р. Дж. Макдонелл, Т. Навицкас, А. Д. Рао, М. Дж. Милликан, Х. Б. Перес-Санчес, Х. Юэнь-Чжоу, М. Дж. Биркук, К. Хемпель, Т. Р. Тан, И. Кассал. «Прямое наблюдение геометрическо-фазовой интерференции в динамике вокруг конического пересечения». Химия природы, 2023; DOI: 10.1038/s41557-023-01300-3
- ^ Лайно, Т.; Д. Пассероне (2004). «Псевдодинамика и оптимизация полос: проливаем свет на конические швы пересечения». Письма по химической физике . 389 (1–3): 1–6. дои : 10.1016/j.cplett.2004.02.110 .
- ^ Мацика, Спиридула; Дэвид Р. Яркони (1 августа 2001 г.). «О влиянии спин-орбитального взаимодействия на конические швы пересечения в молекулах с нечетным числом электронов. I. Обнаружение шва». Журнал химической физики . 115 (5):2038. Бибкод : 2001ЖЧФ.115.2038М . дои : 10.1063/1.1378324 .
- ^ Столов, Альберт; Майкл С. Шурман (2018). «Динамика на конических пересечениях». Ежегодный обзор физической химии . 69 : 427–459. doi : 10.1146/annurev-physchem-052516-050721 . ПМИД 29490199 .
- ^ Фараг, Миннесота; ТСЦ Янсен; Дж. Кнестер (2016). «Исследование межгосударственной связи вблизи конического пересечения с помощью оптической спектроскопии» . Журнал писем по физической химии . 7 (17): 3328–3334. doi : 10.1021/acs.jpclett.6b01463 . ПМИД 27509384 .
- ^ Невилл, Саймон П.; Маджед Шерги; Альберт Столов; Майкл С. Шурман (2018). «Сверхбыстрая рентгеновская спектроскопия конических пересечений». Письма о физических отзывах . 120 (24): 243001. arXiv : 1805.05733 . doi : 10.1103/PhysRevLett.120.243001 . ПМИД 29956989 . S2CID 206312264 .