Плотность (многогранник)

В геометрии плотность , звездчатого многогранника является обобщением понятия числа витков из двух измерений в более высокие измерения представляющее количество витков многогранника вокруг центра симметрии многогранника. Его можно определить, проведя луч от центра до бесконечности, проходя только через грани многогранника, а не через какие-либо элементы более низкой размерности, и подсчитав, через сколько граней он проходит. Для многогранников, у которых это количество не зависит от выбора луча и у которых центральная точка сама не находится ни на одной грани, плотность определяется этим количеством скрещенных граней.
Тот же расчет можно выполнить для любого выпуклого многогранника , даже без симметрии, выбрав любую точку внутри многогранника в качестве его центра. Для этих многогранников плотность будет равна 1.В более общем смысле, для любого несамопересекающегося (акоптического) многогранника плотность может быть вычислена как 1 с помощью аналогичного расчета, который выбирает луч из внутренней точки, который проходит только через грани многогранника, и добавляет единицу, когда этот луч проходит из внутреннюю часть к внешней части многогранника и вычитает единицу, когда этот луч проходит из внешней части многогранника во внутреннюю часть. Однако такое присвоение знаков пересечениям вообще не применимо к звездчатым многогранникам, поскольку они не имеют четко выраженной внутренней и внешней части.
Тесселяции с перекрывающимися гранями могут аналогичным образом определять плотность как количество покрытий граней в любой заданной точке. [1]
Полигоны [ править ]
Плотность многоугольника — это количество раз, которое граница многоугольника оборачивается вокруг его центра. Для выпуклых многоугольников и, в более общем смысле, простых многоугольников (не самопересекающихся) плотность равна 1 по теореме Жордана о кривой .
Плотность многоугольника также можно назвать числом его поворота ; сумма углов поворота всех вершин, деленная на 360°. Это будет целое число для всех уникурсальных путей на плоскости.
Плотность составного многоугольника равна сумме плотностей составляющих его многоугольников.
Правильные звездчатые многоугольники [ править ]
Для правильного звездчатого многоугольника { p / q } плотность равна q . Его можно определить визуально, посчитав минимальное количество пересечений ребер луча от центра до бесконечности.
Примеры [ править ]
- Многоугольник с одним пересечением, такой как этот равносторонний пятиугольник , имеет плотность 0.
- Правильный пятиугольник {5} имеет плотность 1.
- Изотоксальный тетрадекагон , {(7/2) α }, имеет плотность 2, как и обычный {7/2}.
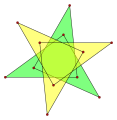
- Гептаграмма {7/3} имеет плотность 3.
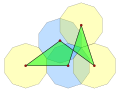
- Изотоксальная гексаграмма (соединение) 2{(3/2) α } имеет плотность 4.
- Изотоксальная додекаграмма {(6/5) α } имеет плотность 5, как и обычная {12/5}.
Многогранники [ править ]
Многогранник и его двойник имеют одинаковую плотность.
Полная кривизна [ править ]
Многогранник можно рассматривать как поверхность с гауссовой кривизной, сосредоточенной в вершинах и определяемой угловым дефектом . Плотность многогранника равна общей кривизне (суммированной по всем его вершинам), деленной на 4π. [2]
Например, куб имеет 8 вершин, в каждой из которых по 3 квадрата , поэтому дефект угла равен π/2. 8×π/2=4π. Значит, плотность куба равна 1.
Простые многогранники [ править ]
Плотность многогранника с простыми гранями и фигурами вершин равна половине эйлеровой характеристики χ. Если его род g , его плотность равна 1- g .
- χ = V − E + F = 2 D = 2(1- g ).
- Плотность топологической сферы многогранника равна единице , как и у куба .
v=8, е=12, f=6. - Плотность рода 1 тороидального многогранника равна нулю , как и в этой шестиугольной форме:
v=24, е=48, f=24. - Плотность тороида рода 5 равна -4 , как у этого Stewart_toroid :
v=72, е=168, f=88.
Правильные звездчатые многогранники [ править ]
Артур Кэли использовал плотность как способ изменить формулу многогранника Эйлера ( V − E + F = 2) для работы с правильными звездчатыми многогранниками , где d v — плотность вершинной фигуры , d f грани и D многогранника. в целом:
Например, большой икосаэдр {3, 5/2} имеет 20 треугольных граней ( d f = 1), 30 ребер и 12 пентаграммных вершинных фигур ( d v = 2), что дает
- 1·20 = 14 = 2 Д. 2·12 − 30 +
Это подразумевает плотность 7. Немодифицированная формула многогранника Эйлера не работает для малого звездчатого додекаэдра {5/2, 5} и его двойственного большого додекаэдра {5, 5/2}, для которых V - E + F = -6.
Правильные звездчатые многогранники существуют в двух двойственных парах, причем каждая фигура имеет ту же плотность, что и ее двойник: одна пара (малый звездчатый додекаэдр — большой додекаэдр) имеет плотность 3, а другая ( большой звездчатый додекаэдр — большой икосаэдр) имеет плотность 7.
 |  |
| Невыпуклый большой икосаэдр {3,5/2} имеет плотность 7, как показано на этом прозрачном виде в поперечном сечении справа. | |
Общие звездчатые многогранники [ править ]
Эдмунд Гесс обобщил формулу звездчатых многогранников с разными типами граней, некоторые из которых могут складываться назад по отношению к другим. Полученное значение плотности соответствует количеству раз, когда соответствующий сферический многогранник покрывает сферу.
Это позволило Кокстеру и соавт. определить плотности большинства однородных многогранников , имеющих один тип вершин и несколько типов граней. [4]
- Плотность восьмиугольной призмы , завернутой дважды, равна 2 , {8/2}×{}, она показана здесь со смещенными вершинами для ясности.
v=16, е=24
ж 1 =8 {4}, ж 2 =2 {8/2}
при d f1 =1, d f2 =2, d v =1. - Плотность пентаграммной призмы {5/2}×{} равна 2 .
v=10, е=15,
ф 1 =5 {4}, ф 2 =2 {5/2},
d f1 =1, d f2 =2.
Неориентируемые многогранники [ править ]
Для полумногогранников , часть граней которых проходит через центр, плотность определить невозможно. Неориентируемые многогранники также не имеют четко определенных плотностей.
Правильные 4-многогранники [ править ]

Существует 10 правильных звездчатых 4-многогранников (называемых 4-многогранниками Шлефли – Гесса ), которые имеют плотности между 4, 6, 20, 66, 76 и 191. Они бывают двойственными парами, за исключением самодвойственного. Цифры плотность-6 и плотность-66.
Примечания [ править ]
- ^ Коксетер, HS M; Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (206–214, Плотность правильных сот в гиперболическом пространстве)
- ^ Геометрия и воображение в Миннеаполисе 17. Угловой дефект многогранника; 20. Кривизна поверхностей; 21. Гауссова кривизна; 27.3.1 Кривизна многогранников стр. 32-51
- ^ Кромвель, П.; Многогранники , CUP хбк (1997), пбк. (1999). (Страница 258)
- ^ Коксетер, 1954 (Раздел 6, Плотность и Таблица 7, Однородные многогранники)
Ссылки [ править ]
- Коксетер, HSM; Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
- Коксетер, HSM ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Серия A. Математические и физические науки , 246 (916): 401–450, doi : 10.1098/rsta.1954.0003 , ISSN 0080-4614 , JSTOR 91532 , MR 0062446
- Веннингер, Магнус Дж. (1979), «Введение в понятие многогранной плотности», Сферические модели , Архив CUP, стр. 132–134 , ISBN 978-0-521-22279-2