Полудифференцируемость

В исчислении понятия односторонней дифференцируемости и полудифференцируемости функции действительнозначной чем , f действительной переменной слабее дифференцируемость . В частности, функция f называется дифференцируемой справа в точке a, если, грубо говоря, производная может быть определена, когда аргумент функции x перемещается в точку a справа, и дифференцируемой слева в точке a, если производная может быть определена как x перемещается влево .

Одномерный случай [ править ]

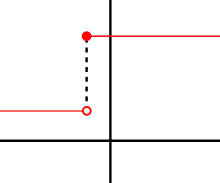
Эта функция не имеет производной в отмеченной точке, так как там функция не является непрерывной . Однако во всех точках он имеет правую производную, причем $\partial _{+}f(a)$ постоянно равен 0.

В математике левая производная и правая производная — это производные (скорости изменения функции), определенные для движения только в одном направлении (влево или вправо; то есть к более низким или более высоким значениям) аргументом функции.

Определения [ править ]

Пусть f обозначает вещественную функцию, определенную на подмножестве I действительных чисел.

Если $a \in I$ — предельная точка I $\cap [$ $a и, \infty)$ односторонний предел

\partial _{+}f(a):=\lim _{\scriptstyle x\to a^{+} \atop \scriptstyle x\in I}{\frac {f(x)-f(a)}{x-a}}

существует как действительное число, то f называется дифференцируемым справа в точке a а предел ∂ ₊ f ( a ) называется правой производной f , в точке a .

Если $a \in I$ — предельная точка $I \cap$ $(-\infty, a]$ и односторонний предел

\partial _{-}f(a):=\lim _{\scriptstyle x\to a^{-} \atop \scriptstyle x\in I}{\frac {f(x)-f(a)}{x-a}}

существует как действительное число, то f называется дифференцируемым слева в точке a а предел ∂ _– f ( a ) называется левой производной f , в точке a .

Если $a \in I$ является предельной точкой $I \cap$ $[a, \infty)$ и $I \cap (-\infty, a]$ и если f дифференцируема слева и справа в точке a , то f называется полудифференцируемой в точке a .

Если левая и правая производные равны, то они имеют то же значение, что и обычная («двунаправленная») производная. Можно также определить симметричную производную , которая равна среднему арифметическому левой и правой производных (если они обе существуют), поэтому симметричная производная может существовать, когда обычная производная не существует. ^[1]

Замечания и примеры [ править ]

Функция дифференцируема во внутренней точке а своей области определения тогда и только тогда, когда она полудифференцируема в точке а и левая производная равна правой производной.
Примером полудифференцируемой функции, которая не является дифференцируемой, является абсолютного значения . функция $f(x)=|x|$ , при a = 0. Легко находим $\partial _{-}f(0)=-1,\partial _{+}f(0)=1.$
Если функция полудифференцируема в точке a , это означает, что она непрерывна в точке a .
Индикаторная функция 1 _[0,∞) дифференцируема справа при каждом вещественном a , но разрывна в нуле (заметим, что эта индикаторная функция не дифференцируема слева в нуле).

Приложение [ править ]

Если вещественная дифференцируемая функция f , определенная на интервале I действительной прямой, имеет всюду нулевую производную, то она постоянна, как применение теоремы о среднем значении показывает . Предположение о дифференцируемости можно ослабить до непрерывности и односторонней дифференцируемости f . Версия для дифференцируемых справа функций приведена ниже, версия для дифференцируемых слева функций аналогична.

Теорема — . Пусть f вещественная непрерывная функция , определенная на произвольном интервале I действительной прямой. Если f дифференцируема справа в каждой точке $a \in I$ , которая не является верхней границей интервала, и если эта правая производная всегда равна нулю, f постоянна то .

Доказательство

Для доказательства от противного предположим, что существует $a < b$ в I такое, что $f (a) \neq f (b)$ . Затем

\varepsilon :={\frac {|f(b)-f(a)|}{2(b-a)}}>0.

Определите c как нижнюю границу всех тех x в интервале $(a, b],$ для которых разностный коэффициент f ε превышает по абсолютной величине, т.е.

c=\inf\{\,x\in (a,b]\mid |f(x)-f(a)|>\varepsilon (x-a)\,\}.

Из непрерывности f следует, что $c < b$ и $| ж (c) - ж (а) | знак равно ε (c - а)$ . В точке c правая производная f по предположению равна нулю, следовательно, существует d в интервале $(c, b]$ с $| f (x) - f (c) | \leq ε (x - c)$ для всех x в $(c, d]$ . Следовательно, по неравенству треугольника ,

|f(x)-f(a)|\leq |f(x)-f(c)|+|f(c)-f(a)|\leq \varepsilon (x-a)

для всех x в $[c, d)$ , что противоречит определению c .

Дифференциальные операторы, действующие слева или справа [ править ]

Другим распространенным применением является описание производных, рассматриваемых как бинарные операторы в инфиксной записи , в которой производные должны применяться либо к левому, либо к правому операнду . Это полезно, например, при определении обобщений скобки Пуассона . Для пары функций f и g левая и правая производные определяются соответственно как

f{\stackrel {\leftarrow }{\partial _{x}}}g={\frac {\partial f}{\partial x}}\cdot g

f{\stackrel {\rightarrow }{\partial }}_{x}g=f\cdot {\frac {\partial g}{\partial x}}.

В нотации бра-кет оператор производной может действовать на правый операнд как регулярную производную или на левый как отрицательную производную. ^[2]

Случай более высокой размерности [ править ]

Это приведенное выше определение можно обобщить на вещественнозначные функции f, определенные на подмножествах R. ^н используя более слабую версию производной по направлению . Пусть a — внутренняя точка области определения f . Тогда f называется полудифференцируемым в точке a, если для любого направления u ∈ R ^н предел

\partial _{u}f(a)=\lim _{h\to 0^{+}}{\frac {f(a+h\,u)-f(a)}{h}}

с $h\in$ R существует как действительное число.

Таким образом, полудифференцируемость слабее, чем дифференцируемость Гато , для которой принимается предел выше h → 0, не ограничивая h только положительными значениями.

Например, функция $f(x,y)={\sqrt {x^{2}+y^{2}}}$ является полудифференцируемым при $(0,0)$ , но там нет дифференцируемого Гато. Действительно, $f(hx,hy)=|h|f(x,y){\text{ and for }}h\geq 0,f(hx,hy)=hf(x,y),f(hx,hy)/h=f(x,y),$ с $a=0,u=(x,y),\partial _{u}f(0)=f(x,y)$

(Обратите внимание, что это обобщение не эквивалентно исходному определению для n = 1, поскольку понятие односторонних предельных точек заменяется более сильным понятием внутренних точек.)

Свойства [ править ]

Любая выпуклая функция на выпуклом открытом подмножестве R ^н является полудифференцируемым.
В то время как каждая полудифференцируемая функция одной переменной непрерывна; это уже не так для нескольких переменных.

Обобщение [ править ]

Вместо вещественных функций можно рассматривать функции, принимающие значения в R. ^н или в банаховом пространстве .

См. также [ править ]

Ссылки [ править ]

^ Питер Р. Мерсер (2014). Подробнее об исчислении одной переменной . Спрингер. п. 173. ИСБН 978-1-4939-1926-0 .
^ Дирак, Поль (1982) [1930]. Принципы квантовой механики . США: Издательство Оксфордского университета. ISBN 978-0198520115 .

Преда, В.; Кицеску, И. (1999). «О квалификации ограничений в задачах многокритериальной оптимизации: полудифференцируемый случай». Дж. Оптим. Теория Прикл . 100 (2): 417–433. дои : 10.1023/А:1021794505701 . S2CID 119868047 .

[Mercer2014-1] Питер Р. Мерсер (2014). Подробнее об исчислении одной переменной . Спрингер. п. 173. ИСБН 978-1-4939-1926-0 .

[2] Дирак, Поль (1982) [1930]. Принципы квантовой механики . США: Издательство Оксфордского университета. ISBN 978-0198520115 .

[1]

[2]