Световое поле

Световое поле или световое поле — это векторная функция , которая описывает количество света, текущего во всех направлениях через каждую точку пространства. Пространство всех возможных световых лучей задается пятимерной пленоптической функцией , а величина каждого луча определяется его яркостью . Майкл Фарадей был первым, кто предложил интерпретировать свет как поле, подобное магнитным полям, над которыми он работал. Термин «световое поле» был введен Андреем Гершуном в классической статье 1936 года о радиометрических свойствах света в трехмерном пространстве.

Термин «поле излучения» также может использоваться для обозначения подобных или идентичных концепции. Этот термин используется в современных исследованиях, таких как поля нейронного излучения.

Пленоптическая функция

Излучение L вдоль луча можно рассматривать как количество света, проходящего по всем возможным прямым линиям через трубку, размер которой определяется ее телесным углом и площадью поперечного сечения.

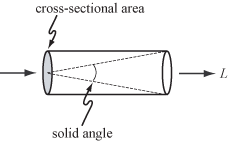
Для геометрической оптики , т. е. для некогерентного света и объектов, размер которых превышает длину волны света, основным носителем света является луч . Мерой количества света, проходящего вдоль луча, является яркость , обозначаемая L и измеряемая в Вт·ср. ⁻¹ ·м ⁻² ; т. е. ватт (Вт) на стерадиан (ср) на квадратный метр (м ² ). Стерадиан является мерой телесного угла , а квадратные метры используются как мера площади поперечного сечения, как показано справа.

Параметризация луча в трехмерном пространстве по положению ( x , y , z ) и направлению ( θ , φ ).

Яркость всех таких лучей в области трехмерного пространства, освещенной неизменным расположением огней, называется пленоптической функцией. Функция пленоптического освещения — это идеализированная функция, используемая в компьютерном зрении и компьютерной графике для выражения изображения сцены из любой возможной позиции просмотра, под любым углом обзора в любой момент времени. На практике он не используется в вычислительных целях, но концептуально полезен для понимания других концепций зрения и графики. Поскольку лучи в пространстве могут быть параметризованы тремя координатами x , y и z и двумя углами θ и φ , как показано слева, это пятимерная функция, то есть функция над пятимерным многообразием, эквивалентная произведение трехмерного евклидова пространства и двухсферы .

Суммирование векторов освещенности D ₁ и D _2, возникающих от двух источников света I ₁ и I _2, дает результирующий вектор D, имеющий показанную величину и направление.

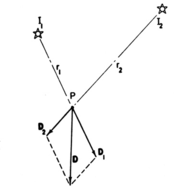
Световое поле в каждой точке пространства можно рассматривать как бесконечный набор векторов, по одному на каждое направление, падающих на точку, с длинами, пропорциональными их яркости.

Интегрирование этих векторов по любому набору источников света или по всей сфере направлений дает одно скалярное значение — общую освещенность в этой точке и результирующее направление. На рисунке показан этот расчет для случая двух источников света. В компьютерной графике эта векторная функция трехмерного пространства называется векторным полем освещенности. Направление вектора в каждой точке поля можно интерпретировать как ориентацию плоской поверхности, расположенной в этой точке, для наиболее яркого ее освещения.

Более высокая размерность

Время, длину волны и угол поляризации можно рассматривать как дополнительные измерения, что соответственно дает функции более высокой размерности.

Световое поле 4D

Излучение вдоль луча остается постоянным, если нет блокаторов.

В пленоптической функции, если область интереса содержит вогнутый объект (например, чашеобразную руку), то свет, выходящий из одной точки объекта, может пройти лишь небольшое расстояние, прежде чем другая точка объекта заблокирует его. Ни одно практическое устройство не могло бы измерить функцию в такой области.

объекта Однако для мест за пределами выпуклой оболочки (например, термоусадочной пленки) пленоптическая функция может быть измерена путем захвата нескольких изображений. В этом случае функция содержит избыточную информацию, поскольку яркость луча остается постоянной по всей его длине. Избыточная информация имеет ровно одно измерение, оставляя четырехмерную функцию, называемую по-разному световым полем, четырехмерным световым полем. или люмиграф. Формально поле определяется как излучение вдоль лучей в пустом пространстве.

Набор лучей в световом поле можно параметризовать различными способами. Наиболее распространенной является двухплоскостная параметризация. Хотя эта параметризация не может представлять все лучи, например, лучи, параллельные двум плоскостям, если плоскости параллельны друг другу, она тесно связана с аналитической геометрией перспективного изображения. Простой способ представить двухплоскостное световое поле — это совокупность перспективных изображений первой плоскости (и любых объектов, которые могут находиться по обе стороны от нее или за ее пределами), каждое из которых взято с позиции наблюдателя на ультрафиолетовой плоскости. Световое поле, параметризованное таким образом, иногда называют световой пластиной.

Некоторые альтернативные параметризации четырехмерного светового поля, которое представляет поток света через пустую область трехмерного пространства. Слева: точки на плоскости или изогнутой поверхности и направления, выходящие из каждой точки. Центр: пары точек на поверхности сферы. Справа: пары точек на двух плоскостях в общем (то есть любом) положении.

Звук аналоговый

Аналогом 4D светового поля для звука является звуковое поле или волновое поле , как при синтезе волнового поля , а соответствующей параметризацией является интеграл Кирхгофа-Гельмгольца , который утверждает, что при отсутствии препятствий звуковое поле во времени равно определяется давлением на самолет. Таким образом, это два измерения информации в любой момент времени и трехмерное поле во времени.

Эта двумерность, по сравнению с кажущейся четырехмерностью света, объясняется тем, что свет распространяется лучами (0D в определенный момент времени, 1D во времени), тогда как согласно принципу Гюйгенса-Френеля звуковой фронт волны можно смоделировать как сферические волны (2D в определенный момент времени, 3D во времени): свет движется в одном направлении (2D информации), а звук распространяется во всех направлениях. Однако свет, распространяющийся в невакуумных средах, может рассеиваться аналогичным образом, и необратимость или потеря информации при рассеянии заметна в кажущейся потере размера системы.

Перефокусировка изображения

Поскольку световое поле предоставляет пространственную и угловую информацию, мы можем изменить положение фокальных плоскостей после воздействия, что часто называют перефокусировкой . Принцип перефокусировки заключается в получении обычных двумерных фотографий из светового поля посредством интегрального преобразования. Преобразование принимает на вход световое поле и генерирует фотографию, сфокусированную на определенной плоскости.

Предполагая $L_{F}(s,t,u,v)$ представляет собой четырехмерное световое поле, которое записывает световые лучи, идущие из положения $(u,v)$ на первой плоскости для позиционирования $(s,t)$ на второй плоскости, где $F$ это расстояние между двумя плоскостями, двумерная фотография на любой глубине. $\alpha F$ можно получить с помощью следующего интегрального преобразования:

${\mathcal {P}}_{\alpha }\left[L_{F}\right](s,t)={1 \over \alpha ^{2}F^{2}}\iint L_{F}\left(u\left(1-{\frac {1}{\alpha }}\right)+{\frac {s}{\alpha }},v\left(1-{\frac {1}{\alpha }}\right)+{\frac {t}{\alpha }},u,v\right)~dudv$,

или более кратко,

${\mathcal {P}}_{\alpha }\left[L_{F}\right]({\boldsymbol {s}})={\frac {1}{\alpha ^{2}F^{2}}}\int L_{F}\left({\boldsymbol {u}}\left(1-{\frac {1}{\alpha }}\right)+{\frac {\boldsymbol {s}}{\alpha }},{\boldsymbol {u}}\right)d{\boldsymbol {u}}$,

где ${\boldsymbol {s}}=(s,t)$, ${\boldsymbol {u}}=(u,v)$, и ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ является фотографом-оператором.

На практике эту формулу нельзя использовать напрямую, поскольку пленоптическая камера обычно фиксирует дискретные образцы светового поля. $L_{F}(s,t,u,v)$, и, следовательно, для вычисления необходима повторная выборка (или интерполяция) ${\textstyle L_{F}\left({\boldsymbol {u}}\left(1-{\frac {1}{\alpha }}\right)+{\frac {\boldsymbol {s}}{\alpha }},{\boldsymbol {u}}\right)}$. Другая проблема – высокая сложность вычислений. Чтобы вычислить $N\times N$ 2-D фотография из $N\times N\times N\times N$ 4-D световое поле, сложность формулы $O(N^{4})$.

Fourier slice photography

One way to reduce the complexity of computation is to adopt the concept of Fourier slice theorem: The photography operator ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ can be viewed as a shear followed by projection. The result should be proportional to a dilated 2-D slice of the 4-D Fourier transform of a light field. More precisely, a refocused image can be generated from the 4-D Fourier spectrum of a light field by extracting a 2-D slice, applying an inverse 2-D transform, and scaling. The asymptotic complexity of the algorithm is $O(N^{2}\operatorname {log} N)$.

Discrete focal stack transform

Another way to efficiently compute 2-D photographs is to adopt discrete focal stack transform (DFST). DFST is designed to generate a collection of refocused 2-D photographs, or so-called Focal Stack. This method can be implemeted by fast fractional fourier transform (FrFT).

The discrete photography operator ${\mathcal {P}}_{\alpha }\left[\cdot \right]$ is defined as follows for a lightfield $L_{F}({\boldsymbol {s}},{\boldsymbol {u}})$ sampled in a 4-D grid ${\boldsymbol {s}}=\Delta s{\tilde {\boldsymbol {s}}},$ ${\tilde {\boldsymbol {s}}}=-{\boldsymbol {n}}_{\boldsymbol {s}},...,{\boldsymbol {n}}_{\boldsymbol {s}}$, ${\boldsymbol {u}}=\Delta u{\tilde {\boldsymbol {u}}},{\tilde {\boldsymbol {u}}}=-{\boldsymbol {n}}_{\boldsymbol {u}},...,{\boldsymbol {n}}_{\boldsymbol {u}}$:

${\mathcal {P}}_{q}[L]({\boldsymbol {s}})=\sum _{{\tilde {\boldsymbol {u}}}=-{\boldsymbol {n}}_{\boldsymbol {u}}}^{{\boldsymbol {n}}_{\boldsymbol {u}}}L({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})\Delta {\boldsymbol {u}},\quad \Delta {\boldsymbol {u}}=\Delta u\Delta v,\quad q=\left(1-{\frac {1}{\alpha }}\right)$

Because $({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})$ is usually not on the 4-D grid, DFST adopts trigonometric interpolation to compute the non-grid values.

The algorithm consists of these steps:

• Sample the light field $L_{F}({\boldsymbol {s}},{\boldsymbol {u}})$ with the sampling period $\Delta s$ and $\Delta u$ and get the discretized light field $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$.
• Pad $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$ with zeros such that the signal length is enough for FrFT without aliasing.
• For every ${\boldsymbol {u}}$, compute the Discrete Fourier transform of $L_{F}^{d}({\boldsymbol {s}},{\boldsymbol {u}})$, and get the result $R1$.
• For every focal length $\alpha F$, compute the fractional fourier transform of $R1$, where the order of the transform depends on $\alpha$, and get the result $R2$.
• Compute the inverse Discrete Fourier transform of $R2$.
• Remove the marginal pixels of $R2$ so that each 2-D photograph has the size $(2{n}_{\boldsymbol {s}}+1)$ by $(2{n}_{\boldsymbol {s}}+1)$

Methods to create light fields

In computer graphics, light fields are typically produced either by rendering a 3D model or by photographing a real scene. In either case, to produce a light field, views must be obtained for a large collection of viewpoints. Depending on the parameterization, this collection typically spans some portion of a line, circle, plane, sphere, or other shape, although unstructured collections are possible.

Devices for capturing light fields photographically may include a moving handheld camera or a robotically controlled camera, an arc of cameras (as in the bullet time effect used in The Matrix), a dense array of cameras, handheld cameras, microscopes, or other optical system.

The number of images in a light field depends on the application. A light field capture of Michelangelo's statue of Night contains 24,000 1.3-megapixel images, which is considered large as of 2022. For light field rendering to completely capture an opaque object, images must be taken of at least the front and back. Less obviously, for an object that lies astride the st plane, finely spaced images must be taken on the uv plane (in the two-plane parameterization shown above).

The number and arrangement of images in a light field, and the resolution of each image, are together called the "sampling" of the 4D light field. Also of interest are the effects of occlusion, lighting and reflection.

Applications

A downward-facing light source (F-F') induces a light field whose irradiance vectors curve outwards. Using calculus, Gershun could compute the irradiance falling on points (P₁, P₂) on a surface.)

Illumination engineering

Gershun's reason for studying the light field was to derive (in closed form) illumination patterns that would be observed on surfaces due to light sources of various shapes positioned above these surface. The branch of optics devoted to illumination engineering is nonimaging optics. It extensively uses the concept of flow lines (Gershun's flux lines) and vector flux (Gershun's light vector). However, the light field (in this case the positions and directions defining the light rays) is commonly described in terms of phase space and Hamiltonian optics.

Light field rendering

Extracting appropriate 2D slices from the 4D light field of a scene, enables novel views of the scene. Depending on the parameterization of the light field and slices, these views might be perspective, orthographic, crossed-slit, general linear cameras, multi-perspective, or another type of projection. Light field rendering is one form of image-based rendering.

Synthetic aperture photography

Integrating an appropriate 4D subset of the samples in a light field can approximate the view that would be captured by a camera having a finite (i.e., non-pinhole) aperture. Such a view has a finite depth of field. Shearing or warping the light field before performing this integration can focus on different fronto-parallel or oblique planes. Images captured by digital cameras that capture the light field can be refocused.

3D display

Presenting a light field using technology that maps each sample to the appropriate ray in physical space produces an autostereoscopic visual effect akin to viewing the original scene. Non-digital technologies for doing this include integral photography, parallax panoramagrams, and holography; digital technologies include placing an array of lenslets over a high-resolution display screen, or projecting the imagery onto an array of lenslets using an array of video projectors. An array of video cameras can capture and display a time-varying light field. This essentially constitutes a 3D television system. Modern approaches to light-field display explore co-designs of optical elements and compressive computation to achieve higher resolutions, increased contrast, wider fields of view, and other benefits.

Brain imaging

Neural activity can be recorded optically by genetically encoding neurons with reversible fluorescent markers such as GCaMP that indicate the presence of calcium ions in real time. Since light field microscopy captures full volume information in a single frame, it is possible to monitor neural activity in individual neurons randomly distributed in a large volume at video framerate. Quantitative measurement of neural activity can be done despite optical aberrations in brain tissue and without reconstructing a volume image, and be used to monitor activity in thousands of neurons.

Generalized scene reconstruction (GSR)

This is a method of 3D reconstruction from multiple images that creates a scene model comprising a generalized light field and a relightable matter field. The generalized light field represents light flowing in every direction through every point in the field. The relightable matter field represents the light interaction properties and emissivity of matter occupying every point in the field. Scene data structures can be implemented using Neural Networks, and Physics-based structures, among others. The light and matter fields are at least partially disentangled.

Holographic stereograms

Image generation and predistortion of synthetic imagery for holographic stereograms is one of the earliest examples of computed light fields.

Glare reduction

Glare arises due to multiple scattering of light inside the camera body and lens optics that reduces image contrast. While glare has been analyzed in 2D image space, it is useful to identify it as a 4D ray-space phenomenon. Statistically analyzing the ray-space inside a camera allows the classification and removal of glare artifacts. In ray-space, glare behaves as high frequency noise and can be reduced by outlier rejection. Such analysis can be performed by capturing the light field inside the camera, but it results in the loss of spatial resolution. Uniform and non-uniform ray sampling can be used to reduce glare without significantly compromising image resolution.

See also

• Angle–sensitive pixel
• Dual photography
• Light-field camera
• Lytro
• Raytrix
• Reflectance paper

References

Theory

• Adelson, E.H., Bergen, J.R. (1991). "The Plenoptic Function and the Elements of Early Vision", In Computation Models of Visual Processing, M. Landy and J.A. Movshon, eds., MIT Press, Cambridge, 1991, pp. 3–20.
• Arvo, J. (1994). "The Irradiance Jacobian for Partially Occluded Polyhedral Sources", Proc. ACM SIGGRAPH, ACM Press, pp. 335–342.
• Bolles, R.C., Baker, H. H., Marimont, D.H. (1987). "Epipolar-Plane Image Analysis: An Approach to Determining Structure from Motion", International Journal of Computer Vision, Vol. 1, No. 1, 1987, Kluwer Academic Publishers, pp 7–55.
• Faraday, M., "Thoughts on Ray Vibrations", Philosophical Magazine, S.3, Vol XXVIII, N188, May 1846.
• Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, pp. 51–151.
• Gortler, S.J., Grzeszczuk, R., Szeliski, R., Cohen, M. (1996). "The Lumigraph", Proc. ACM SIGGRAPH, ACM Press, pp. 43–54.
• Levoy, M., Hanrahan, P. (1996). "Light Field Rendering", Proc. ACM SIGGRAPH, ACM Press, pp. 31–42.
• Moon, P., Spencer, D.E. (1981). The Photic Field, MIT Press.
• Wong, T.T., Fu, C.W., Heng, P.A., Leung C.S. (2002). "The Plenoptic-Illumination Function", IEEE Trans. Multimedia, Vol. 4, No. 3, pp. 361–371.

Analysis

• G. Wetzstein, I. Ihrke, W. Heidrich (2013) "On Plenoptic Multiplexing and Reconstruction", International Journal of Computer Vision (IJCV), Volume 101, Issue 2, pp. 384–400.
• Ramamoorthi, R., Mahajan, D., Belhumeur, P. (2006). "A First Order Analysis of Lighting, Shading, and Shadows", ACM TOG.
• Zwicker, M., Matusik, W., Durand, F., Pfister, H. (2006). "Antialiasing for Automultiscopic 3D Displays", Eurographics Symposium on Rendering, 2006.
• Ng, R. (2005). "Fourier Slice Photography", Proc. ACM SIGGRAPH, ACM Press, pp. 735–744.
• Durand, F., Holzschuch, N., Soler, C., Chan, E., Sillion, F. X. (2005). "A Frequency Analysis of Light Transport", Proc. ACM SIGGRAPH, ACM Press, pp. 1115–1126.
• Chai, J.-X., Tong, X., Chan, S.-C., Shum, H. (2000). "Plenoptic Sampling", Proc. ACM SIGGRAPH, ACM Press, pp. 307–318.
• Halle, M. (1994) "Holographic Stereograms as Discrete imaging systems", in SPIE Proc. Vol. #2176: Practical Holography VIII, S.A. Benton, ed., pp. 73–84.
• Yu, J., McMillan, L. (2004). "General Linear Cameras", Proc. ECCV 2004, Lecture Notes in Computer Science, pp. 14–27.

Cameras

• Marwah, K., Wetzstein, G., Bando, Y., Raskar, R. (2013). "Compressive Light Field Photography using Overcomplete Dictionaries and Optimized Projections", ACM Transactions on Graphics (SIGGRAPH).
• Лян, К.К., Линь, Т.Х., Вонг, Б.И., Лю, К., Чен, Х.Х. (2008). «Фотография с программируемой диафрагмой: получение мультиплексированного светового поля» , Учеб. СИГРАФ ACM .
• Вирарагаван А., Раскар Р., Агравал А., Мохан А., Тамблин Дж. (2007). «Пятнистая фотография: камеры с улучшенной маской для гетеродинных световых полей и перефокусировки кодированной апертуры» , Proc. СИГРАФ ACM .
• Георгиев Т., Чжэн К., Наяр С., Керлесс Б., Салезин Д., Интвала К. (2006). «Компромисс пространственно-углового разрешения в интегральной фотографии» , Учеб. ЭГСР 2006 .
• Канаде Т., Сайто Х., Ведула С. (1998). «Комната 3D: оцифровка изменяющихся во времени 3D-событий с помощью синхронизации нескольких видеопотоков» , технический отчет CMU-RI-TR-98-34, декабрь 1998 г.
• Levoy, M. (2002). Stanford Spherical Gantry .
• Левой М., Нг Р., Адамс А., Футер М., Горовиц М. (2006). «Микроскопия светового поля» , Транзакции ACM с графикой (Proc. SIGGRAPH), Vol. 25, № 3.
• Нг, Р., Левой, М., Бредиф, М., Дюваль, Г., Горовиц, М., Ханрахан, П. (2005). «Фотография светового поля с помощью ручной пленоптической камеры» , Стэнфордский технический отчет CTSR 2005–02, апрель 2005 г.
• Уилберн Б., Джоши Н., Вайш В., Талвала Э., Антунес Э., Барт А., Адамс А., Левой М., Горовиц М. (2005). «Высокопроизводительная обработка изображений с использованием больших массивов камер» , Транзакции ACM с графикой (Proc. SIGGRAPH), Vol. 24, № 3, стр. 765–776.
• Ян, Дж. К., Эверетт, М., Бюлер, К., Макмиллан, Л. (2002). «Камера с распределенным световым полем в реальном времени» , Учеб. Семинар по еврографическому рендерингу 2002 .
• «Камера CAFADIS»

Дисплеи

• Вецштейн Г., Ланман Д., Хирш М., Раскар Р. (2012). «Тензорные дисплеи: отображение компрессионного светового поля с использованием многослойных дисплеев с направленной подсветкой» , Транзакции ACM в графике (SIGGRAPH)
• Вецштейн Г., Ланман Д., Гейдрих В., Раскар Р. (2011). «Многослойное 3D: синтез томографических изображений для дисплеев светового поля на основе затухания и расширенного динамического диапазона» , Транзакции ACM в графике (SIGGRAPH)
• Ланман Д., Ветцштейн Г., Хирш М., Хайдрих В., Раскар Р. (2011). «Поля поляризации: динамическое отображение светового поля с использованием многослойных ЖК-дисплеев» , Транзакции ACM в графике (SIGGRAPH Asia)
• Ланман Д., Хирш М. Ким Ю., Раскар Р. (2010). «HR3D: 3D-дисплей без очков с использованием двухъярусных ЖК-дисплеев. 3D-дисплей высокого ранга с использованием адаптивных к контенту параллаксных барьеров» , ACM Transactions on Graphics (SIGGRAPH Asia)
• Матусик В., Пфистер Х. (2004). «3D-телевидение: масштабируемая система для сбора, передачи и автостереоскопического отображения динамических сцен в реальном времени» , Учеб. ACM SIGGRAPH , ACM Press.
• Джавиди Б., Окано Ф., ред. (2002). Трехмерное телевидение, видео и технологии отображения , Springer-Verlag.
• Клуг М., Бернетт Т., Фанчелло А., Хит А., Гарднер К., О'Коннелл С., Ньюсвангер К. (2013). «Масштабируемая, совместная, интерактивная система отображения светового поля» , Сборник технических документов симпозиума SID
• Фаттал Д., Пэн З., Тран Т., Во С., Фиорентино М., Бруг Дж., Босолей Р. (2013). «Разнонаправленная подсветка для широкоугольного трехмерного дисплея без очков» , Nature 495, 348–351.

Архивы

• "Стэнфордский архив светового поля"
• «Хранилище светового поля UCSD/MERL»
• «Тест светового поля HCI»
• «Архив синтетического светового поля»

Приложения

• Гросеник Л., Андерсон Т., Смит С.Дж. (2009) «Выбор эластичного источника для визуализации ансамблей нейронов in vivo». От нано к макросу, 6-й Международный симпозиум IEEE по биомедицинской визуализации. (2009) 1263–1266.
• Гросеник Л., Брокстон М., Ким С.К., Листон К., Пул Б., Янг С., Андалман А., Шарфф Э., Коэн Н., Ижар О., Рамакришнан , C., Гангули, С., Суппес, П., Левой, М., Дейссерот, К. (2017) «Идентификация динамики клеточной активности в больших объемах тканей в мозгу млекопитающих» bioRxiv 132688; doi: Идентификация динамики клеточной активности в больших объемах тканей головного мозга млекопитающих .
• Хайде Ф., Вецштейн Г., Раскар Р., Хайдрих В. (2013) «Адаптивный синтез изображений для дисплеев со сжатием» , Транзакции ACM в графике (SIGGRAPH)
• Вецштейн, Г., Раскар, Р., Хайдрих, В. (2011) «Ручная шлирен-фотография с зондами светового поля» , Международная конференция IEEE по вычислительной фотографии (ICCP)
• Перес Ф., Маришаль Х.Г., Родригес Х.М. (2008). «Дискретное фокальное стек-преобразование» , Учеб. ЕСИПКО
• Раскар Р., Агравал А., Уилсон К., Вирарагаван А. (2008). «Фотография с учетом бликов: выборка 4D-лучей для уменьшения эффекта бликов объективов фотоаппаратов» , Proc. СИГРАФ ACM.
• Талвала Э.В., Адамс А., Горовиц М., Левой М. (2007). «Вуалирующие блики в изображениях с расширенным динамическим диапазоном» , Учеб. СИГРАФ ACM.
• Галле М., Бентон С., Клюг М., Андеркоффлер Дж. (1991). «Ультраграмма: обобщенная голографическая стереограмма» , SPIE Том. 1461, Практическая голография V , С.А. Бентон, изд., стр. 142–155.
• Зомет А., Фельдман Д., Пелег С., Вайншалл Д. (2003). «Составление мозаики новых взглядов: проекция скрещенных щелей» , Транзакции IEEE по анализу шаблонов и машинному интеллекту (PAMI) , Vol. 25, № 6, июнь 2003 г., стр. 741–754.
• Вайш В., Гарг Г., Талвала Э., Антунес Э., Уилберн Б., Горовиц М., Левой М. (2005). «Фокусировка с синтетической апертурой с использованием факторизации сдвиговой деформации преобразования просмотра» , Proc. Семинар по расширенным 3D-изображениям для обеспечения безопасности и защиты , совместно с CVPR 2005.
• Бедард Н., Шопе Т., Хоберман А., Харалам М.А., Шейх Н., Ковачевич Дж., Балрам Н., Тошич И. (2016). «Дизайн отоскопа светового поля для трехмерной визуализации среднего уха in vivo» . Биомедицинская оптика экспресс , 8 (1), стр. 260–272.
• Каригианни С., Мартинелло М., Спиноулас Л., Фроссар П., Тошич И. (2018). « Автоматическая регистрация барабанной перепонки по данным светового поля ». Международная конференция IEEE по обработке изображений (ICIP)
• Радемахер П., Бишоп Г. (1998). «Многоцентровые проекционные изображения» , Учеб. ACM SIGGRAPH , ACM Press.
• Исаксен А., Макмиллан Л., Гортлер С.Дж. (2000). «Динамически репараметризованные световые поля» , Учеб. ACM SIGGRAPH , ACM Press, стр. 297–306.
• Бюлер К., Боссе М., Макмиллан Л., Гортлер С., Коэн М. (2001). «Неструктурированный люмиграфный рендеринг» , Учеб. ACM SIGGRAPH , ACM Press.
• Эшдаун, И. (1993). «Ближнепольная фотометрия: новый подход» , Журнал Общества светотехники , Vol. 22, № 1, Зима, 1993, стр. 163–180.
• Чавес, Дж. (2015) «Введение в оптику, не создающую изображения, второе издание» , CRC Press
• Уинстон, Р., Миньяно, Дж. К., Бенитес, П. Г., Шац, Н., Бортц, Дж. К., (2005) «Оптика без изображения» , Academic Press
• Пегар, Н.К., Лю Х.И., Антипа, Н., Герлок М., Адесник, Х. и Уоллер, Л.. Компрессионная микроскопия светового поля для трехмерной записи нейронной активности. Оптика 3, нет. 5, стр. 517–524 (2016).
• Леффингвелл Дж., Мигер Д., Махмуд К., Акерсон С. (2018). «Обобщенная реконструкция сцены». arXiv:1803.08496v3 [cs.CV], стр. 1–13.
• Милденхолл Б., Шринивасан П.П., Танчик М., Бэррон Дж.Т., Рамамурти Р. и Нг Р. (2020). «NeRF: представление сцен в виде полей нейронного излучения для синтеза представлений». Компьютерное зрение – ECCV 2020, 405–421.
• Ю А., Фридович-Кейл С., Танчик М., Чен К., Рехт Б., Канадзава А. (2021). «Пленоксели: сияющие поля без нейронных сетей». arXiv:2111.11215, стр. 1–25.
• Перес, CC; Лаури, А; и др. (сентябрь 2015 г.). «Кальциевая нейровизуализация поведения личинок рыбок данио с использованием готовой камеры светового поля» . Журнал биомедицинской оптики . 20 (9): 096009. Бибкод : 2015JBO....20i6009C . дои : 10.1117/1.JBO.20.9.096009 . ПМИД   26358822 .
• Перес, К.С., Лаури, А., Симвулидис, П., Каппетта, М., Эрдманн, А., и Вестмейер, Г.Г. (2015). Нейровизуализация кальция в поведении личинок рыбок данио с использованием готовой к использованию камеры светового поля. Журнал биомедицинской оптики, 20 (9), 096009-096009.
• Леон К., Галвис Л. и Аргуэльо Х. (2016). «Реконструкция мультиспектрального светового поля (5D-пленоптическая функция) на основе компрессионного зондирования с цветными закодированными апертурами из 2D-проекций» Revista Facultad de Ingeniería Universidad de Antioquia 80, стр. 131.