Скрытое распределение Дирихле

Не путать с линейным дискриминантным анализом .

В естественного языка обработке скрытое Дирихле распределение ( LDA ) представляет собой байесовскую сеть (и, следовательно, генеративную статистическую модель ) для моделирования автоматически извлекаемых тем в текстовых корпусах. LDA является примером байесовской тематической модели . При этом наблюдения (например, слова) собираются в документы, и присутствие каждого слова соотносится с одной из тем документа. Каждый документ будет содержать небольшое количество тем.

История

В контексте популяционной генетики LDA была предложена Дж. К. Притчардом , М. Стивенсом и П. Доннелли в 2000 году.

LDA применили в машинном обучении Дэвид Блей , Эндрю Нг и Майкл И. Джордан в 2003 году.

Обзор

Эволюционная биология и биомедицина

В эволюционной биологии и биомедицине модель используется для обнаружения наличия структурированных генетических вариаций в группе людей. Модель предполагает, что аллели , переносимые исследуемыми особями, происходят из различных существующих или прошлых популяций. Модель и различные алгоритмы вывода позволяют ученым оценить частоты аллелей в этих исходных популяциях и происхождение аллелей, переносимых изучаемыми людьми. Исходные популяции можно интерпретировать постфактум с точки зрения различных эволюционных сценариев. В исследованиях ассоциаций обнаружение наличия генетической структуры считается необходимым предварительным шагом, чтобы избежать путаницы .

Клиническая психология, психическое здоровье и социальные науки

В исследованиях клинической психологии LDA использовался для выявления общих тем представлений о себе, с которыми сталкиваются молодые люди в социальных ситуациях. Другие социологи использовали LDA для изучения больших наборов актуальных данных из дискуссий в социальных сетях (например, твитов о рецептурных лекарствах).

Музыковедение

В контексте компьютерного музыкознания LDA использовался для обнаружения тональных структур в различных корпусах.

Машинное обучение

Одно из применений LDA в машинном обучении , в частности обнаружение тем , подзадача обработки естественного языка , заключается в обнаружении тем в коллекции документов, а затем автоматической классификации любого отдельного документа в коллекции с точки зрения того, насколько «релевантным» он является. каждую из обнаруженных тем. Темой . считается набор терминов (т.е. отдельных слов или фраз), которые, взятые вместе, предполагают общую тему

Например, в коллекции документов, связанных с домашними животными, термины «собака» , «спаниель» , «бигль» , « золотистый ретривер » , « щенок » , « лай» « гав» предполагают тему, связанную с DOG_ , а термины «кошка » , «сиамский» , « мейн-кун», «полосатый» , « мэнкс , » и «мяу». , мурлыкать и котенок подскажут тему , связанную с CAT_ . В сборнике может быть еще много тем, например, связанных с питанием, уходом, здравоохранением, поведением и т. д., которые мы для простоты не обсуждаем. (Очень распространенные в языке так называемые стоп-слова – например, «the», «an», «that», «are», «is» и т. д. — не различают темы и обычно отфильтровываются заранее. -обработка перед выполнением LDA также преобразует термины в их «корневые» лексические формы – например, «лай», «лай» и «лай» будут преобразованы в «лай».)

Если коллекция документов достаточно велика, LDA обнаружит такие наборы терминов (т. е. темы) на основе совместного появления отдельных терминов, хотя задача присвоения значимого ярлыка отдельной теме (т. е. того, что все термины DOG_based) зависит от пользователя и часто требует специальных знаний (например, для сбора технической документации). Подход LDA предполагает, что:

1. Семантическое содержание документа состоит из объединения одного или нескольких терминов из одной или нескольких тем.
2. Некоторые термины неоднозначны и относятся к более чем одной теме с разной вероятностью. (Например, термин «тренировка» может применяться как к собакам, так и к кошкам, но чаще всего он относится к собакам, которые используются в качестве рабочих животных или участвуют в соревнованиях по послушанию или навыкам.) Однако в документе сопутствующее присутствие конкретных соседние термины (которые относятся только к одной теме) устранят неоднозначность их использования.
3. Большинство документов будет содержать лишь относительно небольшое количество тем. Например, в коллекции отдельные темы будут встречаться с разной частотой. То есть у них есть распределение вероятностей, так что данный документ с большей вероятностью будет содержать одни темы, чем другие.
4. В рамках темы определенные термины будут использоваться гораздо чаще, чем другие. Другими словами, термины внутри темы также будут иметь свое собственное распределение вероятностей.

Когда используется машинное обучение LDA, оба набора вероятностей вычисляются на этапе обучения с использованием байесовских методов и алгоритма максимизации ожиданий .

LDA представляет собой обобщение более старого подхода вероятностного латентно-семантического анализа (pLSA). Модель pLSA эквивалентна LDA при однородном априорном распределении Дирихле. pLSA опирается только на первые два предположения, приведенные выше, и не заботится об остальных. Хотя оба метода в принципе схожи и требуют от пользователя указания количества тем, которые необходимо обнаружить до начала обучения (как и в случае с кластеризацией K-средних ), LDA имеет следующие преимущества перед pLSA:

• LDA обеспечивает лучшее устранение неоднозначности слов и более точное присвоение документов темам.
• Вычисление вероятностей позволяет использовать «генеративный» процесс, с помощью которого может быть создан набор новых «синтетических документов», который будет точно отражать статистические характеристики исходной коллекции.
• В отличие от LDA, pLSA уязвим к переобучению, особенно при увеличении размера корпуса.
• Алгоритм LDA легче масштабируется для больших наборов данных с использованием подхода MapReduce в вычислительном кластере.

Модель

Обозначение таблички, представляющее модель LDA

С помощью табличной нотации , которая часто используется для представления вероятностных графических моделей (PGM), можно кратко отразить зависимости между многими переменными. Ящики представляют собой «пластины», представляющие реплики, которые представляют собой повторяющиеся объекты. Внешняя пластина представляет документы, а внутренняя пластина представляет повторяющиеся позиции слов в данном документе; каждая позиция связана с выбором темы и слова. Имена переменных определяются следующим образом:

M обозначает количество документов

N — количество слов в данном документе (документ i имеет $N_{i}$ слова)

α - параметр априорного распределения Дирихле по темам каждого документа.

β - параметр априора Дирихле для распределения слов по темам.

$\theta _{i}$ это распределение тем для документа i

$\varphi _{k}$ это распределение слов по теме k

$z_{ij}$ это тема для j -го слова в документе i

$w_{ij}$ это конкретное слово.

Табличное обозначение для LDA с распределением тем и слов, распределенным по Дирихле.

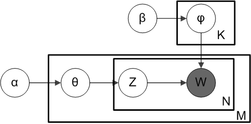
Тот факт, что W выделен серым цветом, означает, что слова $w_{ij}$ являются единственными наблюдаемыми переменными , а остальные переменные являются скрытыми переменными . Как было предложено в оригинальной статье, разреженный априор Дирихле можно использовать для моделирования распределения тем-слов, следуя интуитивному предположению, что распределение вероятностей слов в теме искажено, так что только небольшой набор слов имеет высокую вероятность. Полученная модель является наиболее широко применяемым на сегодняшний день вариантом LDA. Обозначение таблички для этой модели приведено справа, где $K$ обозначает количество тем и $\varphi _{1},\dots ,\varphi _{K}$ являются $V$-мерные векторы, хранящие параметры распределенных по Дирихле распределений тем-слов ( $V$ количество слов в словаре).

Полезно подумать о сущностях, представленных $\theta$ и $\varphi$ как матрицы, созданные путем разложения исходной матрицы «документ-слово», которая представляет корпус моделируемых документов. С этой точки зрения, $\theta$ состоит из строк, определенных документами, и столбцов, определенных темами, а $\varphi$ состоит из строк, определяемых темами, и столбцов, определяемых словами. Таким образом, $\varphi _{1},\dots ,\varphi _{K}$ относится к набору строк или векторов, каждый из которых представляет собой распределение по словам, и $\theta _{1},\dots ,\theta _{M}$относится к набору строк, каждая из которых представляет собой распределение по темам.

Генеративный процесс

Чтобы на самом деле сделать вывод о темах в корпусе, мы представляем себе генеративный процесс, в ходе которого создаются документы, чтобы мы могли сделать вывод или перепроектировать его. Мы представляем себе генеративный процесс следующим образом. Документы представлены как случайные смеси по скрытым темам, где каждая тема характеризуется распределением по всем словам. LDA предполагает следующий генеративный процесс для корпуса $D$ состоящий из $M$ документы каждый длиной $N_{i}$:

1. Выберите $\theta _{i}\sim \operatorname {Dir} (\alpha )$, где $i\in \{1,\dots ,M\}$ и $\mathrm {Dir} (\alpha )$ представляет собой распределение Дирихле с симметричным параметром $\alpha$ которого обычно мало ( $\alpha <1$)

2. Выберите $\varphi _{k}\sim \operatorname {Dir} (\beta )$, где $k\in \{1,\dots ,K\}$ и $\beta$ обычно редко

3. Для каждой из позиций слова $i,j$, где $i\in \{1,\dots ,M\}$, и $j\in \{1,\dots ,N_{i}\}$

а) Выберите тему $z_{i,j}\sim \operatorname {Multinomial} (\theta _{i}).$

(б) Выбери слово $w_{i,j}\sim \operatorname {Multinomial} (\varphi _{z_{i,j}}).$

(Обратите внимание, что полиномиальное распределение здесь относится к полиному только с одним испытанием, который также известен как категориальное распределение .)

Длина $N_{i}$ рассматриваются как независимые от всех других переменных, генерирующих данные ( $w$ и $z$). Нижний индекс часто опускается, как на показанных здесь диаграммах пластин.

Определение

Формальное описание LDA выглядит следующим образом:

Определение переменных в модели

Переменная	Тип	Значение
$K$	целое число	количество тем (например, 50)
$V$	целое число	количество слов в словаре (например, 50 000 или 1 000 000)
$M$	целое число	количество документов
$N_{d=1\dots M}$	целое число	количество слов в документе d
$N$	целое число	общее количество слов во всех документах; сумма всех $N_{d}$ ценности, т.е. $N=\sum _{d=1}^{M}N_{d}$
$\alpha _{k=1\dots K}$	позитивный реальный	предшествующий вес темы k в документе; обычно одинаков для всех тем; обычно число меньше 1, например 0,1, чтобы предпочесть разреженное распределение тем, т. е. несколько тем в документе.
${\boldsymbol {\alpha }}$	K -мерный вектор положительных вещественных чисел	сбор всех $\alpha _{k}$ значения, рассматриваемые как один вектор
$\beta _{w=1\dots V}$	позитивный реальный	предшествующий вес слова w в теме; обычно один и тот же для всех слов; обычно число намного меньше 1, например 0,001, чтобы настоятельно предпочесть разреженное распределение слов, т.е. несколько слов на тему.
${\boldsymbol {\beta }}$	V -мерный вектор положительных вещественных чисел	сбор всех $\beta _{w}$ значения, рассматриваемые как один вектор
$\varphi _{k=1\dots K,w=1\dots V}$	вероятность (действительное число от 0 до 1)	вероятность появления слова w в теме k
${\boldsymbol {\varphi }}_{k=1\dots K}$	V -мерный вектор вероятностей, сумма которого должна равняться 1	распределение слов в теме k
$\theta _{d=1\dots M,k=1\dots K}$	вероятность (действительное число от 0 до 1)	вероятность появления темы k в документе d
${\boldsymbol {\theta }}_{d=1\dots M}$	K -мерный вектор вероятностей, сумма которого должна равняться 1	распределение тем в документе d
$z_{d=1\dots M,w=1\dots N_{d}}$	целое число от 1 до K	идентичность темы слова w в документе d
$\mathbf {Z}$	N -мерный вектор целых чисел от 1 до K	идентичность темы всех слов во всех документах
$w_{d=1\dots M,w=1\dots N_{d}}$	целое число от 1 до V	идентичность слова w в документе d
$\mathbf {W}$	N -мерный вектор целых чисел от 1 до V	идентичность всех слов во всех документах

Затем мы можем математически описать случайные величины следующим образом:

${\begin{aligned}{\boldsymbol {\varphi }}_{k=1\dots K}&\sim \operatorname {Dirichlet} _{V}({\boldsymbol {\beta }})\\{\boldsymbol {\theta }}_{d=1\dots M}&\sim \operatorname {Dirichlet} _{K}({\boldsymbol {\alpha }})\\z_{d=1\dots M,w=1\dots N_{d}}&\sim \operatorname {Categorical} _{K}({\boldsymbol {\theta }}_{d})\\w_{d=1\dots M,w=1\dots N_{d}}&\sim \operatorname {Categorical} _{V}({\boldsymbol {\varphi }}_{z_{dw}})\end{aligned}}$

Вывод

Смотрите также: полиномиальное распределение Дирихле

Изучение различных распределений (набора тем, связанных с ними вероятностей слов, темы каждого слова и конкретной смеси тем каждого документа) является проблемой статистического вывода .

Моделирование Монте-Карло

Оригинальная статья Pritchard et al. использовалась аппроксимация апостериорного распределения методом Монте-Карло. Альтернативное предложение методов вывода включает выборку Гиббса .

Вариационный Байес

В оригинальной статье ML использовалась вариационная байесовская аппроксимация апостериорного распределения .

Максимизация правдоподобия

Прямая оптимизация вероятности с помощью алгоритма блочной релаксации оказывается быстрой альтернативой MCMC.

Неизвестное количество групп/тем

На практике оптимальное количество групп или тем заранее не известно. Его можно оценить аппроксимацией апостериорного распределения цепью Маркова с обратимым скачком Монте-Карло .

Альтернативные подходы

Альтернативные подходы включают распространение ожиданий .

Недавние исследования были сосредоточены на ускорении вывода о скрытом распределении Дирихле для поддержки охвата огромного количества тем в большом количестве документов. Уравнение обновления свернутого семплера Гиббса, упомянутое в предыдущем разделе, имеет естественную разреженность, которой можно воспользоваться. Интуитивно, поскольку каждый документ содержит только подмножество тем. $K_{d}$, и слово также появляется только в подмножестве тем $K_{w}$, приведенное выше уравнение обновления можно переписать, чтобы воспользоваться этой разреженностью.

$p(Z_{d,n}=k)\propto {\frac {\alpha \beta }{C_{k}^{\neg n}+V\beta }}+{\frac {C_{k}^{d}\beta }{C_{k}^{\neg n}+V\beta }}+{\frac {C_{k}^{w}(\alpha +C_{k}^{d})}{C_{k}^{\neg n}+V\beta }}$

В этом уравнении у нас есть три члена, из которых два разреженных, а другой маленький. Мы называем эти термины $a,b$ и $c$ соответственно. Теперь, если мы нормализуем каждый термин, суммируя по всем темам, мы получим:

$A=\sum _{k=1}^{K}{\frac {\alpha \beta }{C_{k}^{\neg n}+V\beta }}$

$B=\sum _{k=1}^{K}{\frac {C_{k}^{d}\beta }{C_{k}^{\neg n}+V\beta }}$

$C=\sum _{k=1}^{K}{\frac {C_{k}^{w}(\alpha +C_{k}^{d})}{C_{k}^{\neg n}+V\beta }}$

Здесь мы можем видеть это $B$ представляет собой суммирование тем, которые появляются в документе $d$, и $C$ также является скудным суммированием тем, о которых говорит слово. $w$ присваивается всему корпусу. $A$ с другой стороны, является плотным, но из-за малых значений $\alpha$ & $\beta$, значение очень мало по сравнению с двумя другими членами.

Теперь, при выборке темы, если мы равномерно выберем случайную величину из $s\sim U(s|\mid A+B+C)$, мы можем проверить, в какую корзину попал наш образец. $A$ мал, мы вряд ли попадем в это ведро; однако, если мы попадем в эту категорию, выборка темы займет $O(K)$ время (то же, что и в оригинальном Collapsed Gibbs Sampler). Однако если мы попадаем в две другие группы, нам нужно будет проверять лишь часть тем, если мы ведем учет редких тем. Тему можно выбрать из $B$ ведро в $O(K_{d})$ время, и тему можно выбрать из $C$ ведро в $O(K_{w})$ время, где $K_{d}$ и $K_{w}$ обозначает количество тем, присвоенных текущему документу и текущему типу слов соответственно.

Обратите внимание, что после выборки каждой темы обновление этих сегментов является базовым. $O(1)$ арифметические операции.

Аспекты вычислительных деталей

Ниже приводится вывод уравнений для свернутой выборки Гиббса , что означает $\varphi$песок $\theta$s будет интегрирован. Для простоты в этом выводе предполагается, что все документы имеют одинаковую длину. $N_{}$. Вывод одинаково действителен, если длина документа различается.

Согласно модели, полная вероятность модели равна:

$P({\boldsymbol {W}},{\boldsymbol {Z}},{\boldsymbol {\theta }},{\boldsymbol {\varphi }};\alpha ,\beta )=\prod _{i=1}^{K}P(\varphi _{i};\beta )\prod _{j=1}^{M}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})P(W_{j,t}\mid \varphi _{Z_{j,t}}),$

где переменные, выделенные жирным шрифтом, обозначают векторную версию переменных. Первый, ${\boldsymbol {\varphi }}$ и ${\boldsymbol {\theta }}$ необходимо интегрироваться.

${\begin{aligned}&P({\boldsymbol {Z}},{\boldsymbol {W}};\alpha ,\beta )=\int _{\boldsymbol {\theta }}\int _{\boldsymbol {\varphi }}P({\boldsymbol {W}},{\boldsymbol {Z}},{\boldsymbol {\theta }},{\boldsymbol {\varphi }};\alpha ,\beta )\,d{\boldsymbol {\varphi }}\,d{\boldsymbol {\theta }}\\={}&\int _{\boldsymbol {\varphi }}\prod _{i=1}^{K}P(\varphi _{i};\beta )\prod _{j=1}^{M}\prod _{t=1}^{N}P(W_{j,t}\mid \varphi _{Z_{j,t}})\,d{\boldsymbol {\varphi }}\int _{\boldsymbol {\theta }}\prod _{j=1}^{M}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d{\boldsymbol {\theta }}.\end{aligned}}$

Все $\theta$независимы друг от друга и одинаковы для всех $\varphi$с. Таким образом, мы можем лечить каждого $\theta$ и каждый $\varphi$ отдельно. Сейчас мы сосредоточимся только на $\theta$ часть.

$\int _{\boldsymbol {\theta }}\prod _{j=1}^{M}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d{\boldsymbol {\theta }}=\prod _{j=1}^{M}\int _{\theta _{j}}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}.$

Далее мы можем сосредоточиться только на одном $\theta$ как следующее:

$\int _{\theta _{j}}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}.$

На самом деле это скрытая часть модели для $j^{th}$ документ. Теперь мы заменим вероятности в приведенном выше уравнении выражением истинного распределения, чтобы записать явное уравнение.

$\int _{\theta _{j}}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}=\int _{\theta _{j}}{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}\prod _{i=1}^{K}\theta _{j,i}^{\alpha _{i}-1}\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}.$

Позволять $n_{j,r}^{i}$ количество словесных токенов в $j^{th}$ документ с тем же символом слова ( $r^{th}$ слово в словаре), присвоенное $i^{th}$ тема. Так, $n_{j,r}^{i}$ является трехмерным. Если какое-либо из трех измерений не ограничено конкретным значением, мы используем точку в скобках. $(\cdot )$ к обозначить. Например, $n_{j,(\cdot )}^{i}$ обозначает количество словесных токенов в $j^{th}$ документ, закрепленный за $i^{th}$ тема. Таким образом, правую часть приведенного выше уравнения можно переписать как:

$\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})=\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot )}^{i}}.$

Итак, $\theta _{j}$ формулу интегрирования можно изменить на:

$\int _{\theta _{j}}{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}\prod _{i=1}^{K}\theta _{j,i}^{\alpha _{i}-1}\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot )}^{i}}\,d\theta _{j}=\int _{\theta _{j}}{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot )}^{i}+\alpha _{i}-1}\,d\theta _{j}.$

Уравнение внутри интегрирования имеет тот же вид, что и распределение Дирихле . Согласно распределению Дирихле ,

$\int _{\theta _{j}}{\frac {\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot )}^{i}+\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (n_{j,(\cdot )}^{i}+\alpha _{i})}}\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot )}^{i}+\alpha _{i}-1}\,d\theta _{j}=1.$

Таким образом,

${\begin{aligned}&\int _{\theta _{j}}P(\theta _{j};\alpha )\prod _{t=1}^{N}P(Z_{j,t}\mid \theta _{j})\,d\theta _{j}=\int _{\theta _{j}}{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot )}^{i}+\alpha _{i}-1}\,d\theta _{j}\\[8pt]={}&{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}{\frac {\prod _{i=1}^{K}\Gamma (n_{j,(\cdot )}^{i}+\alpha _{i})}{\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot )}^{i}+\alpha _{i}\right)}}\int _{\theta _{j}}{\frac {\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot )}^{i}+\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (n_{j,(\cdot )}^{i}+\alpha _{i})}}\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot )}^{i}+\alpha _{i}-1}\,d\theta _{j}\\[8pt]={}&{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}{\frac {\prod _{i=1}^{K}\Gamma (n_{j,(\cdot )}^{i}+\alpha _{i})}{\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot )}^{i}+\alpha _{i}\right)}}.\end{aligned}}$

Теперь мы обратим внимание на ${\boldsymbol {\varphi }}$ часть. Собственно, вывод ${\boldsymbol {\varphi }}$ часть очень похожа на ${\boldsymbol {\theta }}$ часть. Здесь мы лишь перечислим этапы вывода:

${\begin{aligned}&\int _{\boldsymbol {\varphi }}\prod _{i=1}^{K}P(\varphi _{i};\beta )\prod _{j=1}^{M}\prod _{t=1}^{N}P(W_{j,t}\mid \varphi _{Z_{j,t}})\,d{\boldsymbol {\varphi }}\\[8pt]={}&\prod _{i=1}^{K}\int _{\varphi _{i}}P(\varphi _{i};\beta )\prod _{j=1}^{M}\prod _{t=1}^{N}P(W_{j,t}\mid \varphi _{Z_{j,t}})\,d\varphi _{i}\\[8pt]={}&\prod _{i=1}^{K}\int _{\varphi _{i}}{\frac {\Gamma \left(\sum _{r=1}^{V}\beta _{r}\right)}{\prod _{r=1}^{V}\Gamma (\beta _{r})}}\prod _{r=1}^{V}\varphi _{i,r}^{\beta _{r}-1}\prod _{r=1}^{V}\varphi _{i,r}^{n_{(\cdot ),r}^{i}}\,d\varphi _{i}\\[8pt]={}&\prod _{i=1}^{K}\int _{\varphi _{i}}{\frac {\Gamma \left(\sum _{r=1}^{V}\beta _{r}\right)}{\prod _{r=1}^{V}\Gamma (\beta _{r})}}\prod _{r=1}^{V}\varphi _{i,r}^{n_{(\cdot ),r}^{i}+\beta _{r}-1}\,d\varphi _{i}\\[8pt]={}&\prod _{i=1}^{K}{\frac {\Gamma \left(\sum _{r=1}^{V}\beta _{r}\right)}{\prod _{r=1}^{V}\Gamma (\beta _{r})}}{\frac {\prod _{r=1}^{V}\Gamma (n_{(\cdot ),r}^{i}+\beta _{r})}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i}+\beta _{r}\right)}}.\end{aligned}}$

Для наглядности запишем здесь окончательное уравнение с обоими ${\boldsymbol {\phi }}$ и ${\boldsymbol {\theta }}$ интегрированный выход:

$P({\boldsymbol {Z}},{\boldsymbol {W}};\alpha ,\beta )=\prod _{j=1}^{M}{\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}{\frac {\prod _{i=1}^{K}\Gamma (n_{j,(\cdot )}^{i}+\alpha _{i})}{\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot )}^{i}+\alpha _{i}\right)}}\times \prod _{i=1}^{K}{\frac {\Gamma \left(\sum _{r=1}^{V}\beta _{r}\right)}{\prod _{r=1}^{V}\Gamma (\beta _{r})}}{\frac {\prod _{r=1}^{V}\Gamma (n_{(\cdot ),r}^{i}+\beta _{r})}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i}+\beta _{r}\right)}}.$

Целью выборки Гиббса здесь является аппроксимация распределения $P({\boldsymbol {Z}}\mid {\boldsymbol {W}};\alpha ,\beta )$. С $P({\boldsymbol {W}};\alpha ,\beta )$ неизменен для любого из Z, уравнения выборки Гиббса могут быть получены из $P({\boldsymbol {Z}},{\boldsymbol {W}};\alpha ,\beta )$ напрямую. Ключевым моментом является получение следующей условной вероятности:

$P(Z_{(m,n)}\mid {\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha ,\beta )={\frac {P(Z_{(m,n)},{\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha ,\beta )}{P({\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha ,\beta )}},$

где $Z_{(m,n)}$ обозначает $Z$ скрытая переменная $n^{th}$ словесный токен в $m^{th}$ документ. И далее мы предполагаем, что слово символом этого является $v^{th}$ слово в словаре. ${\boldsymbol {Z_{-(m,n)}}}$ обозначает все $Z$но $Z_{(m,n)}$. Обратите внимание, что выборка Гиббса требует только выборки значения для $Z_{(m,n)}$, согласно приведенной выше вероятности, нам не нужно точное значение

$P\left(Z_{m,n}\mid {\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha ,\beta \right)$

но отношения между вероятностями, которые $Z_{(m,n)}$ может иметь значение. Итак, приведенное выше уравнение можно упростить как:

${\begin{aligned}P(&Z_{(m,n)}=v\mid {\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha ,\beta )\\[8pt]&\propto P(Z_{(m,n)}=v,{\boldsymbol {Z_{-(m,n)}}},{\boldsymbol {W}};\alpha ,\beta )\\[8pt]&=\left({\frac {\Gamma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{\prod _{i=1}^{K}\Gamma (\alpha _{i})}}\right)^{M}\prod _{j\neq m}{\frac {\prod _{i=1}^{K}\Gamma \left(n_{j,(\cdot )}^{i}+\alpha _{i}\right)}{\Gamma \left(\sum _{i=1}^{K}n_{j,(\cdot )}^{i}+\alpha _{i}\right)}}\left({\frac {\Gamma \left(\sum _{r=1}^{V}\beta _{r}\right)}{\prod _{r=1}^{V}\Gamma (\beta _{r})}}\right)^{K}\prod _{i=1}^{K}\prod _{r\neq v}\Gamma \left(n_{(\cdot ),r}^{i}+\beta _{r}\right){\frac {\prod _{i=1}^{K}\Gamma \left(n_{m,(\cdot )}^{i}+\alpha _{i}\right)}{\Gamma \left(\sum _{i=1}^{K}n_{m,(\cdot )}^{i}+\alpha _{i}\right)}}\prod _{i=1}^{K}{\frac {\Gamma \left(n_{(\cdot ),v}^{i}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i}+\beta _{r}\right)}}\\[8pt]&\propto {\frac {\prod _{i=1}^{K}\Gamma \left(n_{m,(\cdot )}^{i}+\alpha _{i}\right)}{\Gamma \left(\sum _{i=1}^{K}n_{m,(\cdot )}^{i}+\alpha _{i}\right)}}\prod _{i=1}^{K}{\frac {\Gamma \left(n_{(\cdot ),v}^{i}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i}+\beta _{r}\right)}}\\[8pt]&\propto \prod _{i=1}^{K}\Gamma \left(n_{m,(\cdot )}^{i}+\alpha _{i}\right)\prod _{i=1}^{K}{\frac {\Gamma \left(n_{(\cdot ),v}^{i}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i}+\beta _{r}\right)}}.\end{aligned}}$

Наконец, позвольте $n_{j,r}^{i,-(m,n)}$ иметь то же значение, что и $n_{j,r}^{i}$ но с $Z_{(m,n)}$ исключено. Приведенное выше уравнение можно еще больше упростить, используя свойство гамма-функции . Сначала мы разделяем сумму, а затем объединяем ее обратно, чтобы получить $k$- независимое суммирование, которое можно опустить:

${\begin{aligned}&\propto \prod _{i\neq k}\Gamma \left(n_{m,(\cdot )}^{i,-(m,n)}+\alpha _{i}\right)\prod _{i\neq k}{\frac {\Gamma \left(n_{(\cdot ),v}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i,-(m,n)}+\beta _{r}\right)}}\Gamma \left(n_{m,(\cdot )}^{k,-(m,n)}+\alpha _{k}+1\right){\frac {\Gamma \left(n_{(\cdot ),v}^{k,-(m,n)}+\beta _{v}+1\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{k,-(m,n)}+\beta _{r}+1\right)}}\\[8pt]&=\prod _{i\neq k}\Gamma \left(n_{m,(\cdot )}^{i,-(m,n)}+\alpha _{i}\right)\prod _{i\neq k}{\frac {\Gamma \left(n_{(\cdot ),v}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i,-(m,n)}+\beta _{r}\right)}}\Gamma \left(n_{m,(\cdot )}^{k,-(m,n)}+\alpha _{k}\right){\frac {\Gamma \left(n_{(\cdot ),v}^{k,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{k,-(m,n)}+\beta _{r}\right)}}\left(n_{m,(\cdot )}^{k,-(m,n)}+\alpha _{k}\right){\frac {n_{(\cdot ),v}^{k,-(m,n)}+\beta _{v}}{\sum _{r=1}^{V}n_{(\cdot ),r}^{k,-(m,n)}+\beta _{r}}}\\[8pt]&=\prod _{i}\Gamma \left(n_{m,(\cdot )}^{i,-(m,n)}+\alpha _{i}\right)\prod _{i}{\frac {\Gamma \left(n_{(\cdot ),v}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum _{r=1}^{V}n_{(\cdot ),r}^{i,-(m,n)}+\beta _{r}\right)}}\left(n_{m,(\cdot )}^{k,-(m,n)}+\alpha _{k}\right){\frac {n_{(\cdot ),v}^{k,-(m,n)}+\beta _{v}}{\sum _{r=1}^{V}n_{(\cdot ),r}^{k,-(m,n)}+\beta _{r}}}\\[8pt]&\propto \left(n_{m,(\cdot )}^{k,-(m,n)}+\alpha _{k}\right){\frac {n_{(\cdot ),v}^{k,-(m,n)}+\beta _{v}}{\sum _{r=1}^{V}n_{(\cdot ),r}^{k,-(m,n)}+\beta _{r}}}\end{aligned}}$

Обратите внимание, что та же самая формула выведена в статье о мультиномиальном распределении Дирихле как часть более общего обсуждения интеграции априорных значений распределения Дирихле из байесовской сети .

Связанные проблемы

Похожие модели

Тематическое моделирование — это классическое решение проблемы поиска информации с использованием связанных данных и технологии семантической сети. Связанными моделями и методами являются, среди прочего, скрытое семантическое индексирование , анализ независимых компонентов , вероятностное скрытое семантическое индексирование , неотрицательная матричная факторизация и распределение Гамма-Пуассона .

Модель LDA является модульной и поэтому может быть легко расширена. Основная область интересов – моделирование связей между темами. Это достигается использованием другого распределения на симплексе вместо Дирихле. Модель коррелированных тем следует этому подходу, создавая корреляционную структуру между темами, используя логистическое нормальное распределение вместо Дирихле. Другое расширение — иерархический LDA (hLDA), где темы объединяются в иерархию с помощью вложенного процесса китайского ресторана , структура которого изучается на основе данных. LDA также можно расширить до корпуса, в котором документ включает два типа информации (например, слова и имена), как в модели LDA-dual . Непараметрические расширения LDA включают иерархическую модель смеси процессов Дирихле , которая позволяет неограниченному количеству тем и обучаться на основе данных.

Как отмечалось ранее, pLSA похож на LDA. Модель LDA по сути является байесовской версией модели pLSA. Байесовская формулировка имеет тенденцию работать лучше на небольших наборах данных, поскольку байесовские методы позволяют избежать переобучения данных. Для очень больших наборов данных результаты двух моделей имеют тенденцию сходиться. Единственное отличие состоит в том, что pLSA использует переменную $d$ для представления документа в обучающем наборе. Таким образом, в pLSA при представлении документа, которого модель раньше не видела, мы исправляем $\Pr(w\mid z)$- вероятность слов по темам - быть полученной из обучающего набора и использовать тот же алгоритм EM для вывода $\Pr(z\mid d)$— распределение тем по $d$. Блей утверждает, что этот шаг является мошенничеством, поскольку вы, по сути, подгоняете модель под новые данные.

Пространственные модели

В эволюционной биологии часто естественно предположить, что географическое расположение наблюдаемых особей дает некоторую информацию об их происхождении. В этом суть различных моделей генетических данных с географической привязкой.

Вариации LDA использовались для автоматического распределения естественных изображений по категориям, таким как «спальня» или «лес», обрабатывая изображение как документ, а небольшие участки изображения — как слова; один из вариантов называется пространственным скрытым распределением Дирихле .

См. также

• Вариационные байесовские методы
• Распределение Пачинко
• tf-idf
• Infer.NET

Внешние ссылки

• jLDADMM Пакет Java для моделирования тем на обычных или коротких текстах. jLDADMM включает реализации тематической модели LDA и модели полиномиальной смеси Дирихле «одна тема на документ» . jLDADMM также предоставляет реализацию оценки кластеризации документов для сравнения тематических моделей.
• STTM Пакет Java для моделирования коротких текстовых тем ( https://github.com/qiang2100/STTM ). STTM включает в себя следующие алгоритмы: многочленная смесь Дирихле (DMM) на конференции KDD2014, тематическая модель Biterm (BTM) в журнале TKDE2016, тематическая модель Word Network (WNTM) в журнале KAIS2018, тематическая модель на основе псевдодокументов (PTM) на конференции KDD2016. , Тематическая модель на основе самоагрегации (SATM) на конференции IJCAI2015, (ETM) на конференции PAKDD2017, Обобщенная полиномиальная модель смеси Дирихле на основе урны Поля (GPU) (GPU-DMM) на конференции SIGIR2016, Обобщенная урна Поля (GPU) ) на основе Пуассоновой многочленной модели смеси Дирихле (GPU-PDMM) в журнале TIS2017 и модели скрытых функций с DMM (LF-DMM) в журнале TACL2015. STTM также включает в себя шесть корпусов коротких текстов для оценки. STTM представляет три аспекта оценки производительности алгоритмов (т. е. согласованность тем, кластеризация и классификация).
• Лекция, в которой рассматриваются некоторые обозначения в этой статье: Видеолекция по LDA и тематическому моделированию Дэвида Блея или та же лекция на YouTube.
• Библиография LDA Д. Мимно. Исчерпывающий список ресурсов, связанных с LDA (включая статьи и некоторые реализации).
• Gensim — реализация онлайн-LDA на Python+ NumPy для входных данных, превышающих доступную оперативную память.
• thememodels и lda — это два пакета R для анализа LDA.
• MALLET Пакет на основе Java с открытым исходным кодом из Массачусетского университета в Амхерсте для тематического моделирования с помощью LDA, а также имеет независимо разработанный графический интерфейс - инструмент тематического моделирования.
• LDA в реализации Mahout LDA с использованием MapReduce на Hadoop платформе
• Учебное пособие по скрытому распределению Дирихле (LDA) для платформы машинных вычислений Infer.NET Microsoft Research C# Machine Learning Framework
• LDA в Spark . Начиная с версии 1.3.0, Apache Spark также поддерживает реализацию LDA.
• LDA , пример реализации LDA MATLAB