Логит-нормальное распределение

Логит-нормальный

Функция плотности вероятности
Кумулятивная функция распределения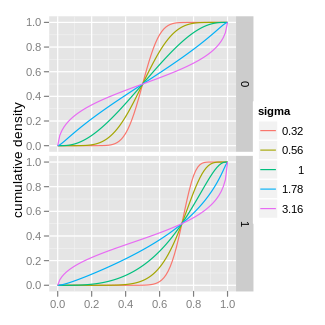
Обозначения	$P({\mathcal {N}}(\mu ,\,\sigma ^{2}))$
Параметры	п 2 > 0 — масштаб в квадрате (реальный), µ ∈ R — местоположение
Поддерживать	х € (0, 1)
PDF	${\frac {1}{\sigma {\sqrt {2\pi }}}}\,e^{-{\frac {(\operatorname {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}{\frac {1}{x(1-x)}}$
CDF	${\frac {1}{2}}{\Big [}1+\operatorname {erf} {\Big (}{\frac {\operatorname {logit} (x)-\mu }{\sqrt {2\sigma ^{2}}}}{\Big )}{\Big ]}$
Иметь в виду	нет аналитического решения
медиана	$P(\mu )\,$
Режим	нет аналитического решения
Дисперсия	нет аналитического решения
МГФ	нет аналитического решения

В теории вероятностей логит -нормальное распределение — это распределение вероятностей случайной величины которой , логит имеет нормальное распределение . Если Y — случайная величина с нормальным распределением, а t — стандартная логистическая функция , то X = t ( Y ) имеет логит-нормальное распределение; аналогично, если X имеет логит-нормальное распределение, то Y = logit ( X ) = log ( X /(1- X )) нормально распределяется. Оно также известно как логистическое нормальное распределение . что часто относится к полиномиальной логит-версии (например, ).

Переменная может быть смоделирована как логит-нормальная, если она представляет собой пропорцию, ограниченную нулем и единицей и где значения нуля и единицы никогда не встречаются.

Характеристика

Функция плотности вероятности

Функция плотности вероятности (PDF) логит-нормального распределения для 0 < x <1:

$f_{X}(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,{\frac {1}{x(1-x)}}\,e^{-{\frac {(\operatorname {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}$

где μ и σ — среднее и стандартное отклонение переменной логита (по определению логит переменной нормально распределен).

Плотность, полученная изменением знака µ, симметрична, поскольку она равна f(1-x;- µ , σ ), смещая моду в другую сторону от 0,5 (середина интервала (0,1) ).

График Logitnormal PDF для различных комбинаций μ (фасетов) и σ (цветов)

Моменты

Моменты логит-нормального распределения не имеют аналитического решения. Моменты можно оценить путем численного интегрирования , однако численное интегрирование может оказаться невозможным, если значения ${\textstyle \mu ,\sigma ^{2}}$таковы, что функция плотности расходится к бесконечности в конечных точках ноль и единица. Альтернативой является использование наблюдения о том, что логит-нормаль является преобразованием нормальной случайной величины. Это позволяет нам аппроксимировать $n$-й момент посредством следующей квазиоценки Монте-Карло $E[X^{n}]\approx {\frac {1}{K-1}}\sum _{i=1}^{K-1}\left(P\left(\Phi _{\mu ,\sigma ^{2}}^{-1}(i/K)\right)\right)^{n},$

где ${\textstyle P}$ стандартная логистическая функция, а ${\textstyle \Phi _{\mu ,\sigma ^{2}}^{-1}}$ - обратная кумулятивная функция распределения нормального распределения со средним значением и дисперсией ${\textstyle \mu ,\sigma ^{2}}$.

Режим или режимы

Когда производная плотности равна 0, тогда положение моды x удовлетворяет следующему уравнению:

$\operatorname {logit} (x)=\sigma ^{2}(2x-1)+\mu .$

Для некоторых значений параметров существует два решения, т.е. распределение бимодальное .

Многомерное обобщение

Логистическое нормальное распределение представляет собой обобщение логит-нормального распределения на D-мерные векторы вероятности путем логистического преобразования многомерного нормального распределения.

Функция плотности вероятности

Функция плотности вероятности :

$f_{X}(\mathbf {x} ;{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {1}{|2\pi {\boldsymbol {\Sigma }}|^{\frac {1}{2}}}}\,{\frac {1}{\prod \limits _{i=1}^{D}x_{i}}}\,e^{-{\frac {1}{2}}\left\{\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)-{\boldsymbol {\mu }}\right\}^{\top }{\boldsymbol {\Sigma }}^{-1}\left\{\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)-{\boldsymbol {\mu }}\right\}}\quad ,\quad \mathbf {x} \in {\mathcal {S}}^{D}\;\;,$

где $\mathbf {x} _{-D}$ обозначает вектор первых (D-1) компонентов $\mathbf {x}$ и ${\mathcal {S}}^{D}$ обозначает симплекс D-мерных векторов вероятности. Это следует из применения аддитивного логистического преобразования для отображения многомерной нормальной случайной величины. $\mathbf {y} \sim {\mathcal {N}}\left({\boldsymbol {\mu }},{\boldsymbol {\Sigma }}\right)\;,\;\mathbf {y} \in \mathbb {R} ^{D-1}$ к симплексу:

$\mathbf {x} =\left[{\frac {e^{y_{1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}}}},\dots ,{\frac {e^{y_{D-1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}}}},{\frac {1}{1+\sum _{i=1}^{D-1}e^{y_{i}}}}\right]^{\top }$

Функции плотности Гаусса и соответствующие функции нормальной логистической плотности после логистического преобразования.

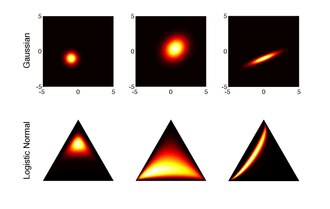
Уникальное обратное отображение задается формулой:

$\mathbf {y} =\left[\log \left({\frac {x_{1}}{x_{D}}}\right),\dots ,\log \left({\frac {x_{D-1}}{x_{D}}}\right)\right]^{\top }$.

Это случай вектора x, сумма компонентов которого равна единице. В случае x с сигмоидальными элементами, т. е. когда

$\mathbf {y} =\left[\log \left({\frac {x_{1}}{1-x_{1}}}\right),\dots ,\log \left({\frac {x_{D}}{1-x_{D}}}\right)\right]^{\top }$

у нас есть

$f_{X}(\mathbf {x} ;{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {1}{|2\pi {\boldsymbol {\Sigma }}|^{\frac {1}{2}}}}\,{\frac {1}{\prod \limits _{i=1}^{D}\left(x_{i}(1-x_{i})\right)}}\,e^{-{\frac {1}{2}}\left\{\log \left({\frac {\mathbf {x} }{1-\mathbf {x} }}\right)-{\boldsymbol {\mu }}\right\}^{\top }{\boldsymbol {\Sigma }}^{-1}\left\{\log \left({\frac {\mathbf {x} }{1-\mathbf {x} }}\right)-{\boldsymbol {\mu }}\right\}}$

где лог и деление в аргументе берутся поэлементно. Это связано с тем, что матрица Якоби преобразования диагональна с элементами ${\frac {1}{x_{i}(1-x_{i})}}$.

Использование в статистическом анализе

Логистическое нормальное распределение является более гибкой альтернативой распределению Дирихле , поскольку оно может фиксировать корреляции между компонентами векторов вероятности. Он также потенциально может упростить статистический анализ композиционных данных , позволяя отвечать на вопросы о логарифмических отношениях компонентов векторов данных. Часто интересуют соотношения, а не абсолютные значения компонентов.

Симплекс вероятностей представляет собой ограниченное пространство, поэтому стандартные методы, обычно применяемые к векторам в $\mathbb {R} ^{n}$ менее значимо. Эйчисон описал проблему ложных отрицательных корреляций при применении таких методов непосредственно к симплициальным векторам. Однако картирование композиционных данных в ${\mathcal {S}}^{D}$ посредством обратной аддитивной логистической трансформации дает реальные данные в $\mathbb {R} ^{D-1}$. К такому представлению данных можно применить стандартные методы. Этот подход оправдывает использование логистического нормального распределения, которое, таким образом, можно рассматривать как «гауссово симплексное распределение».

Связь с распределением Дирихле

Логистическое нормальное приближение к распределению Дирихле

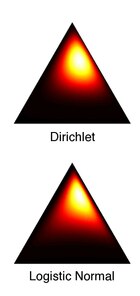
Распределение Дирихле и логистическое нормальное распределение никогда не бывают точно равными при любом выборе параметров. Однако Эйтчисон описал метод аппроксимации Дирихле логистической нормалью, при котором их расхождение Кульбака – Лейблера (KL) минимизируется:

$K(p,q)=\int _{{\mathcal {S}}^{D}}p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)\log \left({\frac {p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)}{q\left(\mathbf {x} \mid {\boldsymbol {\mu }},{\boldsymbol {\Sigma }}\right)}}\right)\,d\mathbf {x}$

Это минимизируется за счет:

${\boldsymbol {\mu }}^{*}=\mathbf {E} _{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]\quad ,\quad {\boldsymbol {\Sigma }}^{*}={\textbf {Var}}_{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]$

Используя моментные свойства распределения Дирихле, решение можно записать в виде дигаммы $\psi$ и тригамма $\psi '$ функции:

$\mu _{i}^{*}=\psi \left(\alpha _{i}\right)-\psi \left(\alpha _{D}\right)\quad ,\quad i=1,\ldots ,D-1$

$\Sigma _{ii}^{*}=\psi '\left(\alpha _{i}\right)+\psi '\left(\alpha _{D}\right)\quad ,\quad i=1,\ldots ,D-1$

$\Sigma _{ij}^{*}=\psi '\left(\alpha _{D}\right)\quad ,\quad i\neq j$

Это приближение особенно точно для больших ${\boldsymbol {\alpha }}$. Фактически, можно показать, что для $\alpha _{i}\rightarrow \infty ,i=1,\ldots ,D$, у нас это есть $p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)\rightarrow q\left(\mathbf {x} \mid {\boldsymbol {\mu }}^{*},{\boldsymbol {\Sigma }}^{*}\right)$.

См. также

• Бета-распределение и распределение Кумарасвами , другие двухпараметрические распределения на ограниченном интервале схожей формы.

Дальнейшее чтение

• Фредерик П. и Лад Ф. (2008) Два момента логитнормального распределения. Коммуникации в статистике, моделировании и вычислениях . 37:1263-1269
• Мид, Р. (1965). «Обобщенное логит-нормальное распределение». Биометрия . 21 (3): 721–732. дои : 10.2307/2528553 . JSTOR   2528553 . ПМИД   5858101 .

Внешние ссылки

• пакет logitnorm для R