Групповая задержка и фазовая задержка

В сигналов обработке групповая задержка и фазовая задержка сигнала — это два связанных способа описания того, как частотные компоненты задерживаются во времени при прохождении через линейную независимую от времени (LTI) систему (например, микрофон , коаксиальный кабель , усилитель , громкоговоритель . , телекоммуникационные системы) система , сетевой кабель , цифровой фильтр или аналоговый фильтр ). Фазовая задержка описывает временной сдвиг синусоидальной составляющей (синусоидальной волны в установившемся состоянии ). Групповая задержка описывает временной сдвиг огибающей волнового пакета , «пакета» или «группы» колебаний, сосредоточенных вокруг одной частоты, которые движутся вместе, сформированных, например, путем умножения ( амплитудной модуляции ) синусоидальной волны на огибающую (например, функция сужения ).

Эти задержки обычно зависят от частоты , это означает, что разные частотные компоненты испытывают разные задержки. сигнала В результате форма испытывает искажения при прохождении через систему. Это искажение может вызвать такие проблемы, как низкая точность воспроизведения аналогового видео и аналогового звука или высокий уровень битовых ошибок в цифровом потоке битов. Однако в идеальном случае постоянной групповой задержки во всем частотном диапазоне сигнала с ограниченной полосой и плоской частотной характеристикой форма сигнала не будет испытывать искажений.

Фон

Частотные составляющие сигнала

Основные статьи: синусоидальная волна , анализ Фурье и линейная нестационарная система.

Анализ Фурье показывает, как сигналы во времени могут быть альтернативно выражены как сумма синусоидальных частотных составляющих , каждая из которых основана на тригонометрической функции. $\sin(x)$ с фиксированной амплитудой и фазой, без начала и конца.

Линейные нестационарные системы обрабатывают каждую синусоидальную составляющую независимо; свойство линейности означает, что они удовлетворяют принципу суперпозиции .

Введение

Свойства групповой и фазовой задержки линейной нестационарной системы (LTI) являются функциями частоты и определяют время с момента появления частотной составляющей изменяющейся во времени физической величины (например, сигнала напряжения) на входе системы LTI. до того момента, когда на выходе системы LTI появится копия той же самой частотной составляющей — возможно, другого физического явления.

Изменяющаяся фазовая характеристика в зависимости от частоты, на основе которой можно рассчитать групповую задержку и фазовую задержку, обычно возникает в таких устройствах, как микрофоны, усилители, громкоговорители, магнитные записывающие устройства, наушники, коаксиальные кабели и фильтры сглаживания. Все частотные составляющие сигнала задерживаются при прохождении через такие устройства или при распространении в пространстве или среде, такой как воздух или вода.

В то время как фазовая характеристика описывает сдвиг фазы в угловых единицах (например, в градусах или радианах ), задержка фазы измеряется в единицах времени и равна отрицательному сдвигу фазы на каждой частоте, деленному на значение этой частоты. Групповая задержка — это отрицательная производная фазового сдвига по частоте.

Фазовая задержка

Линейная независимая от времени система или устройство обладает свойством фазового отклика и свойством фазовой задержки, причем одно из них можно точно вычислить на основе другого. Фазовая задержка напрямую измеряет временную задержку устройства или системы отдельных составляющих синусоидальной частоты в установившемся состоянии . Если функция фазовой задержки на любой заданной частоте (в пределах интересующего диапазона частот) имеет одинаковую константу пропорциональности между фазой на выбранной частоте и самой выбранной частотой, система/устройство будет иметь идеальную линейную фазу , что приводит к с постоянной групповой задержкой. Поскольку фазовая задержка является функцией частоты, дающей задержку времени, отклонение от плоскостности графика ее функции может выявить различия во времени задержки между различными частотными компонентами сигнала , и в этом случае эти различия будут способствовать искажению сигнала, что проявляется в виде выходного сигнала. Форма сигнала сигнала отличается от формы входного сигнала.

Групповая задержка

В то время как фазовая задержка описывает реакцию системы на синусоидальные компоненты установившегося состояния, групповая задержка описывает реакцию на с амплитудной модуляцией синусоиду .

Групповая задержка является удобной мерой линейности фазы по отношению к частоте в системе модуляции. Для сигнала модуляции (сигнала полосы пропускания) информация, переносимая сигналом, передается исключительно в огибающей волны . Поэтому групповая задержка работает только с частотными компонентами, полученными из огибающей.

Базовая система модуляции

Рис. 1. Внешние и внутренние устройства LTI.

Групповую задержку устройства можно точно рассчитать по фазовой характеристике устройства, но не наоборот.

Самый простой вариант использования групповой задержки показан на рисунке 1, где показана концептуальная система модуляции , которая сама по себе является системой LTI с выходным сигналом основной полосы, который в идеале является точной копией входного сигнала основной полосы. Эта система в целом называется здесь внешней системой/устройством LTI, которая содержит внутреннюю (красный блок) систему/устройство LTI. Как это часто бывает в случае радиосистемы, внутренняя красная система LTI на рис. 1 может представлять собой две системы LTI в каскаде, например, усилитель, управляющий передающей антенной на передающей стороне, а другой — антенну и усилитель на приемной стороне.

Амплитудная модуляция

Амплитудная модуляция создает сигнал полосы пропускания путем смещения частотных составляющих основной полосы частот в гораздо более высокий частотный диапазон. Хотя частоты разные, сигнал полосы пропускания несет ту же информацию, что и сигнал основной полосы. Демодулятор делает обратное, сдвигая частоты полосы пропускания обратно в исходный диапазон частот основной полосы. В идеале выходной (модульный) сигнал представляет собой задержанную по времени версию входного (модульного) сигнала, где форма выходного сигнала идентична форме входного сигнала.

На рисунке 1 фазовая задержка внешней системы является значимым показателем производительности. Для амплитудной модуляции внутренняя красная групповая задержка устройства LTI становится внешней фазовой задержкой устройства LTI . Если групповая задержка внутреннего красного устройства полностью плоская в интересующем диапазоне частот, то внешнее устройство будет иметь идеальную фазовую задержку, которая также будет полностью плоской, где вклад искажений из-за фазовой характеристики внешнего устройства LTI определяется полностью из-за возможно другой фазовой характеристики внутреннего устройства - устраняется. В этом случае групповая задержка внутреннего красного устройства и фазовая задержка внешнего устройства дают одинаковую величину временной задержки для сигнала в целом, от входа основной полосы до выхода основной полосы. Важно отметить, что внутреннее (красное) устройство может иметь неплоскую фазовую задержку (но плоскую групповую задержку), в то время как внешнее устройство имеет идеальную идеально ровную фазовую задержку. Это удачно, поскольку в конструкции устройств LTI легче добиться плоской групповой задержки, чем плоской фазовой задержки.

Угловая модуляция

В системе угловой модуляции, например, с частотной модуляцией (FM) или фазовой модуляцией (PM), сигнал полосы пропускания (FM или PM), подаваемый на вход системы LTI, может анализироваться как два отдельных сигнала полосы пропускания, синфазный ( I) сигнал полосы пропускания AM с амплитудной модуляцией и сигнал полосы пропускания AM с квадратурно-фазовой (Q) амплитудной модуляцией, где их сумма точно восстанавливает исходный сигнал полосы пропускания угловой модуляции (FM или PM). Хотя сигнал полосы пропускания (FM/PM) не является амплитудной модуляцией и, следовательно, не имеет видимой внешней огибающей, сигналы полос пропускания I и Q действительно имеют огибающие амплитудной модуляции. (Однако, в отличие от обычной амплитудной модуляции, огибающие I и Q не напоминают форму волны модулирующих сигналов, даже несмотря на то, что 100 процентов модулирующего сигнала представлены их огибающими сложным образом.) Итак, для каждой из Сигналы полос пропускания I и Q, плоская групповая задержка гарантирует, что ни огибающая полосы пропускания I, ни огибающая полосы пропускания Q не будут иметь искажения формы волны, поэтому, когда сигнал полосы пропускания I и сигнал полосы пропускания Q складываются обратно, сумма является исходной. Сигнал полосы пропускания FM/PM, который также не будет изменен.

Теория

Согласно теории систем LTI (используется в теории управления и цифровой или аналоговой обработке сигналов ), выходной сигнал $\displaystyle y(t)$ системы LTI можно определить путем свертки во временной области импульсной характеристики $\displaystyle h(t)$ системы LTI с входным сигналом $\displaystyle x(t)$. Линейная нестационарная система § преобразования Фурье и Лапласа выражает эту связь как:

$y(t)=(h*x)(t)\mathrel {\stackrel {\text{def}}{=}} \int _{-\infty }^{\infty }h(t-\tau )\,x(\tau )\,\mathrm {d} \tau \mathrel {\stackrel {\text{def}}{=}} {\mathcal {L}}^{-1}\{H(s)\,X(s)\}\,,$

где $*$ обозначает операцию свертки, $\displaystyle X(s)$ и $\displaystyle H(s)$ являются преобразованиями Лапласа входных данных $\displaystyle x(t)$ и импульсный отклик $\displaystyle h(t)$, соответственно, s – комплексная частота , а ${\mathcal {L}}^{-1}$ — обратное преобразование Лапласа. $\displaystyle H(s)$ называется передаточной функцией системы LTI и, как и импульсная характеристика $\displaystyle h(t)$, полностью определяет характеристики ввода-вывода системы LTI. Эту свертку можно оценить с помощью интегрального выражения во временной области или (согласно самому правому выражению) с помощью умножения в области Лапласа и последующего применения обратного преобразования для возврата во временную область.

Ответ системы LTI на волновой пакет

Предположим, что такая система приводится в движение волновым пакетом, образованным синусоидой, умноженной на огибающую амплитуды. $\displaystyle A_{\text{env}}(t)>0$, поэтому вход $\displaystyle x(t)$ можно выразить в следующей форме:

$x(t)=A_{\text{env}}(t)\cos(\omega t+\theta )\,.$

Предположим также, что конверт $\displaystyle A_{\text{env}}(t)$ медленно меняется относительно частоты синусоиды $\displaystyle \omega$. Это условие можно выразить математически как:

$\left|{\frac {d}{dt}}\log {\big (}A_{\text{env}}(t){\big )}\right|\ll \omega \ .$

Применение более раннего уравнения свертки показало бы, что выходные данные такой системы LTI очень хорошо аппроксимируются. как:

$y(t)={\big |}H(i\omega ){\big |}\ A_{\text{env}}(t-\tau _{g})\cos {\big (}\omega (t-\tau _{\phi })+\theta {\big )}\;.$

Здесь $\displaystyle \tau _{g}$ групповая задержка и $\displaystyle \tau _{\phi }$ - это фазовая задержка, и они задаются приведенными ниже выражениями (и потенциально являются функциями угловой частоты $\displaystyle \omega$). Фаза синусоиды, на что указывают положения пересечений нуля, задерживается во времени на величину, равную фазовой задержке, $\displaystyle \tau _{\phi }$. Огибающая синусоиды задерживается во времени из-за групповой задержки, $\displaystyle \tau _{g}$.

Математическое определение групповой задержки и фазовой задержки

Групповая задержка , $\displaystyle \tau _{g}$и фазовая задержка , $\displaystyle \tau _{\phi }$, (потенциально) зависят от частоты и может быть вычислен по развернутому фазовому сдвигу $\displaystyle \phi (\omega )$. Фазовая задержка на каждой частоте равна отрицательному сдвигу фазы на этой частоте, деленному на значение этой частоты:

$\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\,.$

Групповая задержка на каждой частоте равна отрицательному наклону ( т. е. производной по частоте) фазы на этой частоте:

$\tau _{g}(\omega )=-{\frac {d\phi (\omega )}{d\omega }}\,.$

В линейной фазовой системе (с неинвертирующим коэффициентом усиления) оба $\displaystyle \tau _{g}$ и $\displaystyle \tau _{\phi }$ постоянны (т.е. не зависят от $\displaystyle \omega$) и равны, а их общее значение равно общей задержке системы; и развернутый фазовый сдвиг системы (а именно $\displaystyle -\omega \tau _{\phi }$) отрицательна, величина которой линейно увеличивается с частотой $\displaystyle \omega$.

Реакция системы LTI на сложную синусоиду

В более общем плане можно показать, что для системы LTI с передаточной функцией $\displaystyle H(s)$ управляется сложной синусоидой единичной амплитуды,

$x(t)=e^{i\omega t}\$

результат

${\begin{aligned}y(t)&=H(i\omega )\ e^{i\omega t}\ \\&=\left({\big |}H(i\omega ){\big |}e^{i\phi (\omega )}\right)\ e^{i\omega t}\ \\&={\big |}H(i\omega ){\big |}\ e^{i\left(\omega t+\phi (\omega )\right)}\ \\\end{aligned}}\$

где фазовый сдвиг $\displaystyle \phi$ является

$\phi (\omega )\ {\stackrel {\mathrm {def} }{=}}\ \arg \left\{H(i\omega )\right\}\;.$

Пример RC-фильтра нижних или верхних частот 1-го порядка

Фаза ФНЧ 1-го порядка , образованная RC-цепью с частотой среза $\omega _{o}{=}{\frac {1}{RC}}$ является:

$$\phi (\omega )=-\arctan({\frac {\omega }{\omega _{o}}})\,.$$

Аналогично, фаза для RC -фильтра верхних частот 1-го порядка :

$$\phi (\omega )={\frac {\pi }{2}}-\arctan({\frac {\omega }{\omega _{o}}})\,.$$

Взяв отрицательную производную по $\omega$ для этого фильтра нижних или верхних частот получается одинаковая групповая задержка:

$${\begin{aligned}\tau _{g}(\omega )&={\frac {\omega _{o}}{\omega ^{2}+\omega _{o}^{2}}}\,.\\\end{aligned}}$$

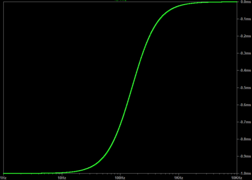
Для частот, значительно меньших частоты среза, фазовая характеристика приблизительно линейна (арктан для небольших входов может быть аппроксимирован линией), поэтому групповая задержка упрощается до постоянного значения:

$${\begin{aligned}\tau _{g}(\omega \ll \omega _{o})&\approx {\frac {1}{\omega _{o}}}=RC\,.\\\end{aligned}}$$

Аналогично, прямо на частоте среза, $\tau _{g}(\omega {=}\omega _{o})={\frac {1}{2\omega _{o}}}={\frac {RC}{2}}\,.$

По мере того, как частоты становятся еще больше, групповая задержка уменьшается обратно пропорционально квадрату частоты и приближается к нулю, когда частота приближается к бесконечности.

Отрицательная групповая задержка

• Рисунок 2. Схема фильтра отрицательной групповой задержки.
• 
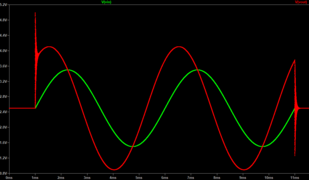
  Схема с отрицательной групповой задержкой $\displaystyle \tau _{g}$ = −RC = −1 мс для частот, значительно меньших, чем 1 ⁄ RC = 1 кГц .
• 
  LTspice AC симуляция $\displaystyle \tau _{g}$ от 1 Гц ( $\displaystyle \tau _{g}$ ≅ −1 мс ) до 10 кГц ( $\displaystyle \tau _{g}$ ≅ 0 мс ).
• 
  Переходное моделирование входной (зеленой) волны, выходной сигнал которой (красный) опережает на 1 мс , но с нестабильностью при включении и выключении входа.

Фильтры будут иметь отрицательную групповую задержку в диапазонах частот, где их фазовая характеристика имеет положительный наклон. Если сигнал ограничен по полосе частот в пределах некоторой максимальной частоты B, то он предсказуем в небольшой степени (в пределах периодов времени, меньших, чем 1 ⁄ Б ). Фильтр, групповая задержка которого отрицательна во всем диапазоне частот этого сигнала, может использовать предсказуемость сигнала, чтобы создать иллюзию непричинного опережения во времени. Однако если сигнал содержит непредсказуемое событие (например, резкое изменение, из-за которого спектр сигнала выходит за пределы полосы пропускания), то иллюзия разрушается. Возможны схемы с отрицательной групповой задержкой (например, рисунок 2), но причинно-следственная связь не нарушается.

Фильтры с отрицательной групповой задержкой могут быть выполнены как в цифровом, так и в аналоговом режиме. Приложения включают компенсацию внутренней задержки фильтров нижних частот для создания фильтров нулевой фазы , которые можно использовать для быстрого обнаружения изменений в тенденциях данных датчиков или цен на акции.

Групповая задержка звука

Групповая задержка имеет определенное значение в области аудио и особенно в области воспроизведения звука. Многие компоненты цепи воспроизведения звука, особенно громкоговорители и многополосные кроссоверные сети громкоговорителей , вносят групповую задержку в аудиосигнал. Поэтому важно знать порог слышимости групповой задержки по частоте, особенно если аудиоцепь должна обеспечивать воспроизведение с высокой точностью . Таблица лучших порогов слышимости была предоставлена ​​Блауэртом и Лоузом.

Частота (кГц)	Порог (РС)	Периоды (Циклы)
0.5	3.2	1.6
1	2	2
2	1	2
4	1.5	6
8	2	16

Фланаган, Мур и Стоун пришли к выводу, что на частотах 1, 2 и 4 кГц групповая задержка около 1,6 мс слышна в наушниках без реверберации. Другие экспериментальные результаты показывают, что когда групповая задержка в диапазоне частот от 300 Гц до 1 кГц ниже 1,0 мс, она не слышна.

Форма волны любого сигнала может быть точно воспроизведена системой, имеющей плоскую частотную характеристику и групповую задержку по всей полосе пропускания сигнала. Лич ввел концепцию дифференциального искажения временной задержки, определяемого как разница между фазовой задержкой и групповой задержкой:

$\Delta \tau =\tau _{\phi }-\tau _{g}$.

Идеальная система должна демонстрировать нулевое или незначительное дифференциальное искажение задержки по времени.

Для коррекции искажений групповой задержки, возникающих из-за использования кроссоверов в многополосных акустических системах, можно использовать методы цифровой обработки сигналов. Это включает в себя значительное вычислительное моделирование акустических систем для успешного применения выравнивания задержки. с использованием алгоритма проектирования равнопульсационного фильтра FIR Паркса-Макклеллана .

Групповая задержка в оптике

Групповая задержка важна в физике и, в частности, в оптике .

В оптическом волокне групповая задержка — это время прохождения, необходимое оптической энергии , распространяющейся с моды данной групповой скоростью , для прохождения заданного расстояния. оптического волокна Для целей измерения дисперсии интересующей величиной является групповая задержка на единицу длины, которая является обратной величиной групповой скорости конкретной моды. Измеренная групповая задержка сигнала, проходящего через оптическое волокно, зависит от длины волны из-за различных механизмов дисперсии, присутствующих в волокне.

Часто желательно, чтобы групповая задержка была постоянной на всех частотах; в противном случае происходит временное размытие сигнала. Поскольку групповая задержка ${\textstyle \tau _{g}(\omega )=-{\frac {d\phi }{d\omega }}}$, следовательно, постоянная групповая задержка может быть достигнута, если передаточная функция устройства или среды имеет линейную фазовую характеристику (т. е. $\phi (\omega )=\phi (0)-\tau _{g}\omega$ где групповая задержка $\tau _{g}$ является константой). Степень нелинейности фазы указывает на отклонение групповой задержки от постоянного значения.

Дифференциальная групповая задержка представляет собой разницу во времени распространения между двумя собственными X и Y. поляризации модами Рассмотрим две собственные моды 0 ° и 90 ° , которые представляют собой состояния линейной поляризации . Если состояние поляризации входного сигнала является линейным состоянием под углом 45 ° между двумя собственными модами, входной сигнал делится поровну на две собственные моды. Мощность передаваемого сигнала E _{T ,total} представляет собой комбинацию передаваемых сигналов режимов x и y .

$E_{T}=(E_{i,x}\cdot t_{x})^{2}+(E_{i,y}\cdot t_{y})^{2}\,$

Дифференциальная групповая задержка D _t определяется как разница во времени распространения между собственными модами: D _t = | т _{т , Икс} - т _{т , y} |.

Истинная задержка времени

Говорят, что передающее устройство имеет истинную временную задержку (TTD), если временная задержка не зависит от частоты электрического сигнала. TTD обеспечивает широкую мгновенную полосу сигнала практически без искажений сигнала, таких как расширение импульса во время импульсной работы.

TTD является важной характеристикой линий передачи без потерь и с низкими потерями, без дисперсии . Уравнения телеграфиста § Передача без потерь показывает, что сигналы распространяются через них со скоростью $1/{\sqrt {LC}}$ для распределенной индуктивности L и C. емкости Следовательно, задержка распространения любого сигнала по линии просто равна длине линии, разделенной на эту скорость.

Групповая задержка из полиномов передаточной функции

Если передаточная функция или Sij параметра рассеяния находится в форме полиномиального преобразования Лапласа , то математическое определение групповой задержки, приведенное выше, может быть решено аналитически в замкнутой форме. Полиномиальная функция передаточная $P(S)$ можно взять с собой $j\omega$ оси и определяется как $P(j\omega )$. $\phi (\omega )$ может быть определено из $P(j\omega )$, а затем групповую задержку можно определить, решив $-d\phi (\omega )|/d\omega$.

определить $\phi (\omega )$ от $P(j\omega )$, используйте определение $\phi (\omega )=tan^{-1}(P(j\omega )_{imag}/P(j\omega )_{real})$. При условии $j^{2N}$ всегда реален и $j^{2N+1}$всегда воображаемо, $\phi (\omega )$ может быть переопределено как $\phi (\omega )=tan^{-1}(-jP(j\omega )_{odd}/P(j\omega )_{even})$ где четные и нечетные относятся к полиномам, которые содержат только коэффициенты четного или нечетного порядка соответственно. $-j$ в числителе просто преобразует мнимое $P(j\omega )_{odd}$ числитель к действительному значению, так как $P(j\omega )_{odd}$ само по себе является чисто воображаемым.

${\begin{aligned}&{\frac {dtan^{-1}(f(x))}{dx}}={\frac {df(x)/dx}{1+f(x)^{2}}}\\&f(x)={\frac {-jP(j\omega )_{odd}}{P(j\omega )_{even}}}\\&{\frac {df(x)}{dx}}={\frac {P(j\omega )_{even}{\frac {d(P(j\omega )_{odd})}{dx}}--jP(j\omega )_{odd}{\frac {d(-jP(j\omega )_{even})}{dx}}}{P(j\omega )_{even}^{2}}}\end{aligned}}$

Приведенные выше выражения содержат четыре условия для расчета:

${\begin{array}{lcl}Se=P(j\omega )_{even}&=&\sum _{k=0}^{N/2}P_{2k}(j\omega )^{2k}&=&\sum _{k=0}^{N/2}P_{2k}(-1)^{k}(\omega )^{2k}\\So=P(j\omega )_{odd}&=&-j\sum _{k=1}^{(N+1)/2}P_{2k-1}(j\omega )^{2k-1}&=&\sum _{k=1}^{(N+1)/2}P_{2k-1}(-1)^{k-1}(\omega )^{2k-1}\\De={\frac {d(P(j\omega )_{even})}{dx}}&=&-j\sum _{k=1}^{N/2}2kP_{2k}(j\omega )^{2k-1}&=&\sum _{k=1}^{N/2}2kP_{2k}(-1)^{k-1}(\omega )^{2k-1}\\Do={\frac {d(P(j\omega )_{odd})}{dx}}&=&\sum _{k=1}^{(N+1)/2}{(2k-1)}P_{2k-1}(j\omega )^{2k-2}&=&\sum _{k=1}^{(N+1)/2}{(2k-1)}P_{2k-1}(-1)^{k-1}(\omega )^{2k-2}\\\\{\frac {df(x)}{dx}}&=&{\frac {SeDo-SoDe}{Se^{2}}}\end{array}}$

Приведенные выше уравнения можно использовать для определения групповой задержки полинома $P(S)$ в закрытом виде, показанном ниже после приведения уравнений к упрощенному виду.

${\text{Group Delay}}=gd(P(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}=-{\frac {(So*De+Se*Do)}{(Se^{2}+So^{2})}}{\text{ sec}}$

Полиномиальное соотношение

Полиномиальное отношение вида $P2(S)=P_{num}(S)/P_{den}(S)$, например, обычно встречающееся в определении конструкции фильтра , может иметь групповую задержку, определяемую с использованием фазового соотношения, $\phi (P1/P2)=\phi (P1)-\phi (P2)$.

${\text{Group Delay}}=gd(P2)=gd(P2_{num})-gd(P2_{den})sec$

Простой пример фильтра

Передаточная функция четырехполюсного фильтра Лежандра, используемая в примере фильтра Лежандра, показана ниже.

$T_{4}(j\omega )={\frac {1}{2.4494897(j\omega )^{4}+3.8282201(j\omega )^{3}+4.6244874(j\omega )^{2}+3.0412127(j\omega )+1}}$

Групповая задержка числителя при проверке равна нулю, поэтому необходимо определить только групповую задержку знаменателя.

${\begin{aligned}&Pe_{den}=2.4494897\omega ^{4}-4.6244874\omega ^{2}+1\\&Po_{den}=-3.8282201\omega ^{3}+3.0412127\omega \\&De_{den}=4(2.4494897)\omega ^{3}-2(4.6244874)\omega \\&Do_{den}=3(-3.8282201)\omega ^{2}+3.0412127\end{aligned}}$

Оценка в $\omega$ = 1 рад/сек:

${\begin{aligned}&Pe_{den}=-1.1749977\\&Po_{den}=-0.7870074\\&De_{den}=-0.548984\\&Do_{den}=-8.4434476\end{aligned}}$

${\begin{aligned}&{\text{Group Delay}}=gd(T_{4}(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}\\&={\bigg [}0--{\frac {((-0.7870074*-0.548984)+(-1.1749977*-8.4434476))}{((-1.1749977)^{2}+(-0.7870074)^{2})}}{\bigg ]}\\&=5.1765430{\text{ sec}}\\&{\text{at }}\omega =1{\text{ rad/sec}}\end{aligned}}$

Правильность процедуры и результатов расчета групповой задержки можно подтвердить путем сравнения их с результатами, полученными на основе цифровой производной фазового угла. $\phi (\omega )$, используя небольшую дельту $\Delta \omega$ +/-1.e-04 рад/сек.

${\begin{aligned}&{\text{Group Delay}}=gd(T_{4}(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}\\&=-(\phi (1+1e-04)-\phi (1.-1e04))/2e-04\\&=5.1765432{\text{ sec}}\\&{\text{at }}\omega =1{\text{ rad/sec}}\end{aligned}}$

Поскольку групповая задержка, рассчитанная с помощью цифровой производной с использованием небольшой дельты, находится в пределах 7 знаков точности по сравнению с точным аналитическим расчетом, процедура расчета групповой задержки и результаты подтверждаются правильностью.

Отклонение от линейной фазы

Отклонение от линейной фазы , $\phi _{DLP}(\omega )$, иногда называемый просто «отклонением фазы», ​​представляет собой разницу между фазовой характеристикой, $\phi (\omega )$, а линейная часть фазовой характеристики $\phi _{L}(\omega )$, и является полезным измерением для определения линейности $\phi (\omega )$.

Удобный способ измерения $\phi _{DLP}(\omega )$ состоит в том, чтобы взять простую линейную регрессию $\phi (\omega )$ выборку в интересующем диапазоне частот и вычитание ее из фактического $\phi (\omega )$. $\phi _{DLP}(\omega )$ Ожидается, что идеальная линейная фазовая характеристика будет иметь значение 0 во всем интересующем диапазоне частот (например, в полосе пропускания фильтра), в то время как $\phi _{DLP}(\omega )$ Реальная приблизительно линейная фазовая характеристика может отклоняться от 0 на небольшую конечную величину в интересующем диапазоне частот.

Преимущество перед групповой задержкой

Преимущество измерения или расчета $\phi _{DLP}(\omega )$ чрезмерное измерение или расчет групповой задержки, $gd(\omega )$, является $\phi _{DLP}(\omega )$ всегда сходится к 0, когда фаза становится линейной, тогда как $gd(\omega )$ сходится к конечной величине, которая может быть неизвестна заранее. Учитывая это, функцию оптимизации линейной фазы легче реализовать с помощью $\phi _{DLP}(\omega ){=}0$ цель, чем с $gd(\omega ){=}constant$ цель, когда значение для $constant$ не обязательно уже известно.

См. также

• Замеры аудиосистемы
• Линейная фаза
• Фильтр Бесселя — фильтр нижних частот с максимально плоской групповой задержкой.
• Фильтр Лежандра — из раздела примеров
• Рисунок глаз
• Групповая скорость — «Групповая скорость света в среде обратна групповой задержке на единицу длины».
• Фазовая скорость
• Волновой пакет

Ссылки

В этой статье использованы общедоступные материалы из Федеральный стандарт 1037C . Управление общего обслуживания . Архивировано из оригинала 22 января 2022 г.

Внешние ссылки

• Обсуждение групповой задержки в громкоговорителях
• Пояснения и применение групповой задержки
• «Введение в цифровые фильтры с аудиоприложениями», Джулиус О. Смит III (издание, сентябрь 2007 г.).