Extension of the scalar spherical harmonics for use with vector fields
В математике векторные сферические гармоники ( VSH ) являются расширением скалярных сферических гармоник для использования с векторными полками . Компоненты VSH являются сложными функциями, выраженными в векторах сферической координат .
Несколько конвенций были использованы для определения VSH. [ 1 ] [ 2 ] [ 3 ] [ 4 ] [ 5 ] et al. Полем Учитывая скалярную сферическую гармонику y ℓm ( θ , φ )
Y
ℓ
m
=
Y
ℓ
m
r
^
,
{\displaystyle \mathbf {Y} _{\ell m}=Y_{\ell m}{\hat {\mathbf {r} }},}
Ψ
ℓ
m
=
r
∇
Y
ℓ
m
,
{\displaystyle \mathbf {\Psi } _{\ell m}=r\nabla Y_{\ell m},}
Φ
ℓ
m
=
r
×
∇
Y
ℓ
m
,
{\displaystyle \mathbf {\Phi } _{\ell m}=\mathbf {r} \times \nabla Y_{\ell m},}
с
r
^
{\displaystyle {\hat {\mathbf {r} }}}
единичным вектором вдоль радиального направления в сферических координатах и
r
{\displaystyle \mathbf {r} }
r
=
r
r
^
{\displaystyle \mathbf {r} =r{\hat {\mathbf {r} }}}
Интерес этих новых векторных полей состоит в том, чтобы отделить радиальную зависимость от угловой при использовании сферических координат, так что векторное поле допускает расширение мультиоля
E
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
E
ℓ
m
r
(
r
)
Y
ℓ
m
+
E
ℓ
m
(
1
)
(
r
)
Ψ
ℓ
m
+
E
ℓ
m
(
2
)
(
r
)
Φ
ℓ
m
)
.
{\displaystyle \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(E_{\ell m}^{r}(r)\mathbf {Y} _{\ell m}+E_{\ell m}^{(1)}(r)\mathbf {\Psi } _{\ell m}+E_{\ell m}^{(2)}(r)\mathbf {\Phi } _{\ell m}\right).}
Метки на компонентах отражают, что
E
ℓ
m
r
{\displaystyle E_{\ell m}^{r}}
E
ℓ
m
(
1
)
{\displaystyle E_{\ell m}^{(1)}}
E
ℓ
m
(
2
)
{\displaystyle E_{\ell m}^{(2)}}
r
{\displaystyle \mathbf {r} }
Как скалярные сферические гармоники, VSH удовлетворяет
Y
ℓ
,
−
m
=
(
−
1
)
m
Y
ℓ
m
∗
,
Ψ
ℓ
,
−
m
=
(
−
1
)
m
Ψ
ℓ
m
∗
,
Φ
ℓ
,
−
m
=
(
−
1
)
m
Φ
ℓ
m
∗
,
{\displaystyle {\begin{aligned}\mathbf {Y} _{\ell ,-m}&=(-1)^{m}\mathbf {Y} _{\ell m}^{*},\\\mathbf {\Psi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Psi } _{\ell m}^{*},\\\mathbf {\Phi } _{\ell ,-m}&=(-1)^{m}\mathbf {\Phi } _{\ell m}^{*},\end{aligned}}}
который сокращает количество независимых функций примерно пополам. Звезда указывает на сложное сопряжение .
VSH ортогональны в обычном трехмерном способе в каждой точке
r
{\displaystyle \mathbf {r} }
Y
ℓ
m
(
r
)
⋅
Ψ
ℓ
m
(
r
)
=
0
,
Y
ℓ
m
(
r
)
⋅
Φ
ℓ
m
(
r
)
=
0
,
Ψ
ℓ
m
(
r
)
⋅
Φ
ℓ
m
(
r
)
=
0.
{\displaystyle {\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0,\\\mathbf {\Psi } _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell m}(\mathbf {r} )&=0.\end{aligned}}}
Они также ортогональны в пространстве Гильберта:
∫
Y
ℓ
m
⋅
Y
ℓ
′
m
′
∗
d
Ω
=
δ
ℓ
ℓ
′
δ
m
m
′
,
∫
Ψ
ℓ
m
⋅
Ψ
ℓ
′
m
′
∗
d
Ω
=
ℓ
(
ℓ
+
1
)
δ
ℓ
ℓ
′
δ
m
m
′
,
∫
Φ
ℓ
m
⋅
Φ
ℓ
′
m
′
∗
d
Ω
=
ℓ
(
ℓ
+
1
)
δ
ℓ
ℓ
′
δ
m
m
′
,
∫
Y
ℓ
m
⋅
Ψ
ℓ
′
m
′
∗
d
Ω
=
0
,
∫
Y
ℓ
m
⋅
Φ
ℓ
′
m
′
∗
d
Ω
=
0
,
∫
Ψ
ℓ
m
⋅
Φ
ℓ
′
m
′
∗
d
Ω
=
0.
{\displaystyle {\begin{aligned}\int \mathbf {Y} _{\ell m}\cdot \mathbf {Y} _{\ell 'm'}^{*}\,d\Omega &=\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {\Phi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=\ell (\ell +1)\delta _{\ell \ell '}\delta _{mm'},\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Psi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {Y} _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=0,\\\int \mathbf {\Psi } _{\ell m}\cdot \mathbf {\Phi } _{\ell 'm'}^{*}\,d\Omega &=0.\end{aligned}}}
Дополнительный результат в одной точке
r
{\displaystyle \mathbf {r} }
ℓ
,
m
,
ℓ
′
,
m
′
{\displaystyle \ell ,m,\ell ',m'}
Y
ℓ
m
(
r
)
⋅
Ψ
ℓ
′
m
′
(
r
)
=
0
,
Y
ℓ
m
(
r
)
⋅
Φ
ℓ
′
m
′
(
r
)
=
0.
{\displaystyle {\begin{aligned}\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Psi } _{\ell 'm'}(\mathbf {r} )&=0,\\\mathbf {Y} _{\ell m}(\mathbf {r} )\cdot \mathbf {\Phi } _{\ell 'm'}(\mathbf {r} )&=0.\end{aligned}}}
Отношения ортогональности позволяют вычислить сферические многополиные моменты векторного поля как
E
ℓ
m
r
=
∫
E
⋅
Y
ℓ
m
∗
d
Ω
,
E
ℓ
m
(
1
)
=
1
ℓ
(
ℓ
+
1
)
∫
E
⋅
Ψ
ℓ
m
∗
d
Ω
,
E
ℓ
m
(
2
)
=
1
ℓ
(
ℓ
+
1
)
∫
E
⋅
Φ
ℓ
m
∗
d
Ω
.
{\displaystyle {\begin{aligned}E_{\ell m}^{r}&=\int \mathbf {E} \cdot \mathbf {Y} _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(1)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Psi } _{\ell m}^{*}\,d\Omega ,\\E_{\ell m}^{(2)}&={\frac {1}{\ell (\ell +1)}}\int \mathbf {E} \cdot \mathbf {\Phi } _{\ell m}^{*}\,d\Omega .\end{aligned}}}
Учитывая мультипольное расширение скалярного поля
ϕ
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
ϕ
ℓ
m
(
r
)
Y
ℓ
m
(
θ
,
ϕ
)
,
{\displaystyle \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\phi _{\ell m}(r)Y_{\ell m}(\theta ,\phi ),}
Мы можем выразить его градиент с точки зрения VSH как
∇
ϕ
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
d
ϕ
ℓ
m
d
r
Y
ℓ
m
+
ϕ
ℓ
m
r
Ψ
ℓ
m
)
.
{\displaystyle \nabla \phi =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {d\phi _{\ell m}}{dr}}\mathbf {Y} _{\ell m}+{\frac {\phi _{\ell m}}{r}}\mathbf {\Psi } _{\ell m}\right).}
Для любого мультипольного поля у нас есть
∇
⋅
(
f
(
r
)
Y
ℓ
m
)
=
(
d
f
d
r
+
2
r
f
)
Y
ℓ
m
,
∇
⋅
(
f
(
r
)
Ψ
ℓ
m
)
=
−
ℓ
(
ℓ
+
1
)
r
f
Y
ℓ
m
,
∇
⋅
(
f
(
r
)
Φ
ℓ
m
)
=
0.
{\displaystyle {\begin{aligned}\nabla \cdot \left(f(r)\mathbf {Y} _{\ell m}\right)&=\left({\frac {df}{dr}}+{\frac {2}{r}}f\right)Y_{\ell m},\\\nabla \cdot \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}fY_{\ell m},\\\nabla \cdot \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=0.\end{aligned}}}
По суперпозиции мы получаем дивергенцию любого векторного поля:
∇
⋅
E
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
d
E
ℓ
m
r
d
r
+
2
r
E
ℓ
m
r
−
ℓ
(
ℓ
+
1
)
r
E
ℓ
m
(
1
)
)
Y
ℓ
m
.
{\displaystyle \nabla \cdot \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {dE_{\ell m}^{r}}{dr}}+{\frac {2}{r}}E_{\ell m}^{r}-{\frac {\ell (\ell +1)}{r}}E_{\ell m}^{(1)}\right)Y_{\ell m}.}
Мы видим, что компонент на φ ℓM соленоидальный .
Для любого мультипольного поля у нас есть
∇
×
(
f
(
r
)
Y
ℓ
m
)
=
−
1
r
f
Φ
ℓ
m
,
∇
×
(
f
(
r
)
Ψ
ℓ
m
)
=
(
d
f
d
r
+
1
r
f
)
Φ
ℓ
m
,
∇
×
(
f
(
r
)
Φ
ℓ
m
)
=
−
ℓ
(
ℓ
+
1
)
r
f
Y
ℓ
m
−
(
d
f
d
r
+
1
r
f
)
Ψ
ℓ
m
.
{\displaystyle {\begin{aligned}\nabla \times \left(f(r)\mathbf {Y} _{\ell m}\right)&=-{\frac {1}{r}}f\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Psi } _{\ell m}\right)&=\left({\frac {df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Phi } _{\ell m},\\\nabla \times \left(f(r)\mathbf {\Phi } _{\ell m}\right)&=-{\frac {\ell (\ell +1)}{r}}f\mathbf {Y} _{\ell m}-\left({\frac {df}{dr}}+{\frac {1}{r}}f\right)\mathbf {\Psi } _{\ell m}.\end{aligned}}}
Под суперпозицией мы получаем срок любого векторного поля:
∇
×
E
=
∑
ℓ
=
0
∞
∑
m
=
−
ℓ
ℓ
(
−
ℓ
(
ℓ
+
1
)
r
E
ℓ
m
(
2
)
Y
ℓ
m
−
(
d
E
ℓ
m
(
2
)
d
r
+
1
r
E
ℓ
m
(
2
)
)
Ψ
ℓ
m
+
(
−
1
r
E
ℓ
m
r
+
d
E
ℓ
m
(
1
)
d
r
+
1
r
E
ℓ
m
(
1
)
)
Φ
ℓ
m
)
.
{\displaystyle \nabla \times \mathbf {E} =\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(-{\frac {\ell (\ell +1)}{r}}E_{\ell m}^{(2)}\mathbf {Y} _{\ell m}-\left({\frac {dE_{\ell m}^{(2)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(2)}\right)\mathbf {\Psi } _{\ell m}+\left(-{\frac {1}{r}}E_{\ell m}^{r}+{\frac {dE_{\ell m}^{(1)}}{dr}}+{\frac {1}{r}}E_{\ell m}^{(1)}\right)\mathbf {\Phi } _{\ell m}\right).}
Действие оператора Лапласа
Δ
=
∇
⋅
∇
{\displaystyle \Delta =\nabla \cdot \nabla }
Δ
(
f
(
r
)
Z
ℓ
m
)
=
(
1
r
2
∂
∂
r
r
2
∂
f
∂
r
)
Z
ℓ
m
+
f
(
r
)
Δ
Z
ℓ
m
,
{\displaystyle \Delta \left(f(r)\mathbf {Z} _{\ell m}\right)=\left({\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}r^{2}{\frac {\partial f}{\partial r}}\right)\mathbf {Z} _{\ell m}+f(r)\Delta \mathbf {Z} _{\ell m},}
Z
ℓ
m
=
Y
ℓ
m
,
Ψ
ℓ
m
,
Φ
ℓ
m
{\displaystyle \mathbf {Z} _{\ell m}=\mathbf {Y} _{\ell m},\mathbf {\Psi } _{\ell m},\mathbf {\Phi } _{\ell m}}
Δ
Y
ℓ
m
=
−
1
r
2
(
2
+
ℓ
(
ℓ
+
1
)
)
Y
ℓ
m
+
2
r
2
Ψ
ℓ
m
,
Δ
Ψ
ℓ
m
=
2
r
2
ℓ
(
ℓ
+
1
)
Y
ℓ
m
−
1
r
2
ℓ
(
ℓ
+
1
)
Ψ
ℓ
m
,
Δ
Φ
ℓ
m
=
−
1
r
2
ℓ
(
ℓ
+
1
)
Φ
ℓ
m
.
{\displaystyle {\begin{aligned}\Delta \mathbf {Y} _{\ell m}&=-{\frac {1}{r^{2}}}(2+\ell (\ell +1))\mathbf {Y} _{\ell m}+{\frac {2}{r^{2}}}\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Psi } _{\ell m}&={\frac {2}{r^{2}}}\ell (\ell +1)\mathbf {Y} _{\ell m}-{\frac {1}{r^{2}}}\ell (\ell +1)\mathbf {\Psi } _{\ell m},\\\Delta \mathbf {\Phi } _{\ell m}&=-{\frac {1}{r^{2}}}\ell (\ell +1)\mathbf {\Phi } _{\ell m}.\end{aligned}}}
Также обратите внимание, что это действие становится симметричным , т.е. неагональные коэффициенты равны
2
r
2
ℓ
(
ℓ
+
1
)
{\textstyle {\frac {2}{r^{2}}}{\sqrt {\ell (\ell +1)}}}
нормализованного VSH.
ℓ
=
0
{\displaystyle \ell =0}
Y
00
=
1
4
π
r
^
,
Ψ
00
=
0
,
Φ
00
=
0
.
{\displaystyle {\begin{aligned}\mathbf {Y} _{00}&={\sqrt {\frac {1}{4\pi }}}{\hat {\mathbf {r} }},\\\mathbf {\Psi } _{00}&=\mathbf {0} ,\\\mathbf {\Phi } _{00}&=\mathbf {0} .\end{aligned}}}
ℓ
=
1
{\displaystyle \ell =1}
Y
10
=
3
4
π
cos
θ
r
^
,
Y
11
=
−
3
8
π
e
i
φ
sin
θ
r
^
,
{\displaystyle {\begin{aligned}\mathbf {Y} _{10}&={\sqrt {\frac {3}{4\pi }}}\cos \theta \,{\hat {\mathbf {r} }},\\\mathbf {Y} _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\sin \theta \,{\hat {\mathbf {r} }},\end{aligned}}}
Ψ
10
=
−
3
4
π
sin
θ
θ
^
,
Ψ
11
=
−
3
8
π
e
i
φ
(
cos
θ
θ
^
+
i
φ
^
)
,
{\displaystyle {\begin{aligned}\mathbf {\Psi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\theta } }},\\\mathbf {\Psi } _{11}&=-{\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(\cos \theta \,{\hat {\mathbf {\theta } }}+i\,{\hat {\mathbf {\varphi } }}\right),\end{aligned}}}
Φ
10
=
−
3
4
π
sin
θ
φ
^
,
Φ
11
=
3
8
π
e
i
φ
(
i
θ
^
−
cos
θ
φ
^
)
.
{\displaystyle {\begin{aligned}\mathbf {\Phi } _{10}&=-{\sqrt {\frac {3}{4\pi }}}\sin \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi } _{11}&={\sqrt {\frac {3}{8\pi }}}e^{i\varphi }\left(i\,{\hat {\mathbf {\theta } }}-\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}}
ℓ
=
2
{\displaystyle \ell =2}
Y
20
=
1
4
5
π
(
3
cos
2
θ
−
1
)
r
^
,
Y
21
=
−
15
8
π
sin
θ
cos
θ
e
i
φ
r
^
,
Y
22
=
1
4
15
2
π
sin
2
θ
e
2
i
φ
r
^
.
{\displaystyle {\begin{aligned}\mathbf {Y} _{20}&={\frac {1}{4}}{\sqrt {\frac {5}{\pi }}}\,(3\cos ^{2}\theta -1)\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{21}&=-{\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,\cos \theta \,e^{i\varphi }\,{\hat {\mathbf {r} }},\\\mathbf {Y} _{22}&={\frac {1}{4}}{\sqrt {\frac {15}{2\pi }}}\,\sin ^{2}\theta \,e^{2i\varphi }\,{\hat {\mathbf {r} }}.\end{aligned}}}
Ψ
20
=
−
3
2
5
π
sin
θ
cos
θ
θ
^
,
Ψ
21
=
−
15
8
π
e
i
φ
(
cos
2
θ
θ
^
+
i
cos
θ
φ
^
)
,
Ψ
22
=
15
8
π
sin
θ
e
2
i
φ
(
cos
θ
θ
^
+
i
φ
^
)
.
{\displaystyle {\begin{aligned}\mathbf {\Psi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\,\sin \theta \,\cos \theta \,{\hat {\mathbf {\theta } }},\\\mathbf {\Psi } _{21}&=-{\sqrt {\frac {15}{8\pi }}}\,e^{i\varphi }\,\left(\cos 2\theta \,{\hat {\mathbf {\theta } }}+i\cos \theta \,{\hat {\mathbf {\varphi } }}\right),\\\mathbf {\Psi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{2i\varphi }\,\left(\cos \theta \,{\hat {\mathbf {\theta } }}+i\,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}}
Φ
20
=
−
3
2
5
π
sin
θ
cos
θ
φ
^
,
Φ
21
=
15
8
π
e
i
φ
(
i
cos
θ
θ
^
−
cos
2
θ
φ
^
)
,
Φ
22
=
15
8
π
sin
θ
e
2
i
φ
(
−
i
θ
^
+
cos
θ
φ
^
)
.
{\displaystyle {\begin{aligned}\mathbf {\Phi } _{20}&=-{\frac {3}{2}}{\sqrt {\frac {5}{\pi }}}\sin \theta \,\cos \theta \,{\hat {\mathbf {\varphi } }},\\\mathbf {\Phi } _{21}&={\sqrt {\frac {15}{8\pi }}}\,e^{i\varphi }\,\left(i\cos \theta \,{\hat {\mathbf {\theta } }}-\cos 2\theta \,{\hat {\mathbf {\varphi } }}\right),\\\mathbf {\Phi } _{22}&={\sqrt {\frac {15}{8\pi }}}\,\sin \theta \,e^{2i\varphi }\,\left(-i\,{\hat {\mathbf {\theta } }}+\cos \theta \,{\hat {\mathbf {\varphi } }}\right).\end{aligned}}}
Выражения для отрицательных значений М получены путем применения отношений симметрии.
VSH особенно полезен в изучении мультипольных полей радиации . Например, магнитный мульпол обусловлен колебательным током с угловой частотой
ω
{\displaystyle \omega }
J
^
=
J
(
r
)
Φ
ℓ
m
,
{\displaystyle {\hat {\mathbf {J} }}=J(r)\mathbf {\Phi } _{\ell m},}
и соответствующие электрические и магнитные поля могут быть написаны как
E
^
=
E
(
r
)
Φ
ℓ
m
,
B
^
=
B
r
(
r
)
Y
ℓ
m
+
B
(
1
)
(
r
)
Ψ
ℓ
m
.
{\displaystyle {\begin{aligned}{\hat {\mathbf {E} }}&=E(r)\mathbf {\Phi } _{\ell m},\\{\hat {\mathbf {B} }}&=B^{r}(r)\mathbf {Y} _{\ell m}+B^{(1)}(r)\mathbf {\Psi } _{\ell m}.\end{aligned}}}
Заменив уравнения Максвелла, закон Гаусса автоматически удовлетворяется
∇
⋅
E
^
=
0
,
{\displaystyle \nabla \cdot {\hat {\mathbf {E} }}=0,}
в то время как закон Фарадея разъезжает как
∇
×
E
^
=
−
i
ω
B
^
⇒
{
ℓ
(
ℓ
+
1
)
r
E
=
i
ω
B
r
,
d
E
d
r
+
E
r
=
i
ω
B
(
1
)
.
{\displaystyle \nabla \times {\hat {\mathbf {E} }}=-i\omega {\hat {\mathbf {B} }}\quad \Rightarrow \quad {\begin{cases}{\dfrac {\ell (\ell +1)}{r}}E=i\omega B^{r},\\{\dfrac {dE}{dr}}+{\dfrac {E}{r}}=i\omega B^{(1)}.\end{cases}}}
Закон Гаусса для магнитного поля подразумевает
∇
⋅
B
^
=
0
⇒
d
B
r
d
r
+
2
r
B
r
−
ℓ
(
ℓ
+
1
)
r
B
(
1
)
=
0
,
{\displaystyle \nabla \cdot {\hat {\mathbf {B} }}=0\quad \Rightarrow \quad {\frac {dB^{r}}{dr}}+{\frac {2}{r}}B^{r}-{\frac {\ell (\ell +1)}{r}}B^{(1)}=0,}
и уравнение Ampère -Maxwell дает
∇
×
B
^
=
μ
0
J
^
+
i
μ
0
ε
0
ω
E
^
⇒
−
B
r
r
+
d
B
(
1
)
d
r
+
B
(
1
)
r
=
μ
0
J
+
i
ω
μ
0
ε
0
E
.
{\displaystyle \nabla \times {\hat {\mathbf {B} }}=\mu _{0}{\hat {\mathbf {J} }}+i\mu _{0}\varepsilon _{0}\omega {\hat {\mathbf {E} }}\quad \Rightarrow \quad -{\frac {B^{r}}{r}}+{\frac {dB^{(1)}}{dr}}+{\frac {B^{(1)}}{r}}=\mu _{0}J+i\omega \mu _{0}\varepsilon _{0}E.}
Таким образом, уравнения дифференциальных частиц были преобразованы в набор обычных дифференциальных уравнений.
Угловая часть магнитных и электрических векторных сферических гармоник. Красные и зеленые стрелы показывают направление поля. Также представлены генерация скалярных функций, показаны только первые три порядка (диполи, квадруполи, октаколи). Во многих приложениях векторные сферические гармоники определяются как фундаментальный набор решений уравнения векторного Гельмгольца в сферических координатах. [ 6 ] [ 7 ]
В этом случае векторные сферические гармоники генерируются скалярными функциями, которые являются решениями скалярного уравнения Гельмгольца с волновым вектором
k
{\displaystyle \mathbf {k} }
ψ
e
m
n
=
cos
m
φ
P
n
m
(
cos
ϑ
)
z
n
(
k
r
)
ψ
o
m
n
=
sin
m
φ
P
n
m
(
cos
ϑ
)
z
n
(
k
r
)
{\displaystyle {\begin{array}{l}{\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\\{\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}\end{array}}}
P
n
m
(
cos
θ
)
{\displaystyle P_{n}^{m}(\cos \theta )}
полиномы Legendre , и
z
n
(
k
r
)
{\displaystyle z_{n}({k}r)}
сферических функций Бесселя .
Векторные сферические гармоники определяются как:
продольные гармоники
L
o
e
m
n
=
∇
ψ
o
e
m
n
{\displaystyle \mathbf {L} _{^{e}_{o}mn}=\mathbf {\nabla } \psi _{^{e}_{o}mn}}
Магнитные гармоники
M
o
e
m
n
=
∇
×
(
r
ψ
o
e
m
n
)
{\displaystyle \mathbf {M} _{^{e}_{o}mn}=\nabla \times \left(\mathbf {r} \psi _{^{e}_{o}mn}\right)}
Электрические гармоники
N
o
e
m
n
=
∇
×
M
o
e
m
n
k
{\displaystyle \mathbf {N} _{^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{k}}}
Здесь мы используем Harmonics реальную угловую часть, где
m
≥
0
{\displaystyle m\geq 0}
Давайте представим нотацию
ρ
=
k
r
{\displaystyle \rho =kr}
M
e
m
n
(
k
,
r
)
=
−
m
sin
(
θ
)
sin
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
z
n
(
ρ
)
e
θ
−
cos
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
z
n
(
ρ
)
e
φ
{\displaystyle {\begin{aligned}{\mathbf {M} _{emn}(k,\mathbf {r} )=\qquad {{\frac {-m}{\sin(\theta )}}\sin(m\varphi )P_{n}^{m}(\cos(\theta ))}z_{n}(\rho )\mathbf {e} _{\theta }}\\{{}-\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}z_{n}(\rho )\mathbf {e} _{\varphi }\end{aligned}}}
M
o
m
n
(
k
,
r
)
=
m
sin
(
θ
)
cos
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
z
n
(
ρ
)
e
θ
−
sin
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
z
n
(
ρ
)
e
φ
{\displaystyle {\begin{aligned}{\mathbf {M} _{omn}(k,\mathbf {r} )=\qquad {{\frac {m}{\sin(\theta )}}\cos(m\varphi )P_{n}^{m}(\cos(\theta ))}}z_{n}(\rho )\mathbf {e} _{\theta }\\{{}-\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}z_{n}(\rho )\mathbf {e} _{\varphi }}\end{aligned}}}
N
e
m
n
(
k
,
r
)
=
z
n
(
ρ
)
ρ
cos
(
m
φ
)
n
(
n
+
1
)
P
n
m
(
cos
(
θ
)
)
e
r
+
cos
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
θ
−
m
sin
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
sin
(
θ
)
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
φ
{\displaystyle {\begin{aligned}{\mathbf {N} _{emn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\cos(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }}\\{{}+\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{{}-m\sin(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}
N
o
m
n
(
k
,
r
)
=
z
n
(
ρ
)
ρ
sin
(
m
φ
)
n
(
n
+
1
)
P
n
m
(
cos
(
θ
)
)
e
r
+
sin
(
m
φ
)
d
P
n
m
(
cos
(
θ
)
)
d
θ
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
θ
+
m
cos
(
m
φ
)
P
n
m
(
cos
(
θ
)
)
sin
(
θ
)
1
ρ
d
d
ρ
[
ρ
z
n
(
ρ
)
]
e
φ
{\displaystyle {\begin{aligned}\mathbf {N} _{omn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\sin(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }\\{}+\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{}+{m\cos(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}
ρ
{\displaystyle \rho }
ρ
{\displaystyle \rho }
Продольные гармоники:
L
o
e
m
n
(
k
,
r
)
=
∂
∂
r
z
n
(
k
r
)
P
n
m
(
cos
θ
)
sin
cos
m
φ
e
r
+
1
r
z
n
(
k
r
)
∂
∂
θ
P
n
m
(
cos
θ
)
sin
cos
m
φ
e
θ
∓
m
r
sin
θ
z
n
(
k
r
)
P
n
m
(
cos
θ
)
cos
sin
m
φ
e
φ
{\displaystyle {\begin{aligned}\mathbf {L} _{^{e}_{o}{mn}}(k,\mathbf {r} ){}=\qquad &{\frac {\partial }{\partial r}}z_{n}(kr)P_{n}^{m}(\cos \theta ){^{\cos }_{\sin }}{m\varphi }\mathbf {e} _{r}\\{}+{}&{\frac {1}{r}}z_{n}(kr){\frac {\partial }{\partial \theta }}P_{n}^{m}(\cos \theta ){^{\cos }_{\sin }}m\varphi \mathbf {e} _{\theta }\\{}\mp {}&{\frac {m}{r\sin \theta }}z_{n}(kr)P_{n}^{m}(\cos \theta ){^{\sin }_{\cos }}m\varphi \mathbf {e} _{\varphi }\end{aligned}}}
Решения векторного уравнения Гельмгольца подчиняются следующим отношениям ортогональности: [ 7 ]
∫
0
2
π
∫
0
π
L
o
e
m
n
⋅
L
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
(
2
n
+
1
)
2
(
n
+
m
)
!
(
n
−
m
)
!
k
2
{
n
[
z
n
−
1
(
k
r
)
]
2
+
(
n
+
1
)
[
z
n
+
1
(
k
r
)
]
2
}
∫
0
2
π
∫
0
π
M
o
e
m
n
⋅
M
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
2
n
+
1
(
n
+
m
)
!
(
n
−
m
)
!
n
(
n
+
1
)
[
z
n
(
k
r
)
]
2
∫
0
2
π
∫
0
π
N
o
e
m
n
⋅
N
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
(
2
n
+
1
)
2
(
n
+
m
)
!
(
n
−
m
)
!
n
(
n
+
1
)
{
(
n
+
1
)
[
z
n
−
1
(
k
r
)
]
2
+
n
[
z
n
+
1
(
k
r
)
]
2
}
∫
0
π
∫
0
2
π
L
o
e
m
n
⋅
N
o
e
m
n
sin
ϑ
d
ϑ
d
φ
=
(
1
+
δ
m
,
0
)
2
π
(
2
n
+
1
)
2
(
n
+
m
)
!
(
n
−
m
)
!
n
(
n
+
1
)
k
{
[
z
n
−
1
(
k
r
)
]
2
−
[
z
n
+
1
(
k
r
)
]
2
}
{\displaystyle {\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {L} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}k^{2}\left\{n\left[z_{n-1}(kr)\right]^{2}+(n+1)\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {M} _{^{e}_{o}mn}\cdot \mathbf {M} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{2n+1}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left[z_{n}(kr)\right]^{2}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {N} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left\{(n+1)\left[z_{n-1}(kr)\right]^{2}+n\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{\pi }\int _{0}^{2\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)k\left\{\left[z_{n-1}(kr)\right]^{2}-\left[z_{n+1}(kr)\right]^{2}\right\}\end{aligned}}}
Все другие интегралы по углам между различными функциями или функциями с разными индексами равны нулю.
Иллюстрация трансформации векторных сферических гармоник под ротациями. Можно видеть, что они преобразуются так же, как и соответствующие скалярные функции. При вращении векторные сферические гармоники преобразуются друг через друга так же, как и соответствующие скалярные сферические функции , которые генерируются для определенного типа векторных гармоник. Например, если генерирующие функции являются обычными сферическими гармониками , то векторные гармоники также будут преобразованы через D-Matrices Wigner [ 8 ] [ 9 ] [ 10 ]
D
^
(
α
,
β
,
γ
)
Y
J
M
(
s
)
(
θ
,
φ
)
=
∑
M
′
=
−
J
J
[
D
M
M
′
(
J
)
(
α
,
β
,
γ
)
]
∗
Y
J
M
′
(
s
)
(
θ
,
φ
)
,
{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )\mathbf {Y} _{JM}^{(s)}(\theta ,\varphi )=\sum _{M'=-J}^{J}[D_{MM'}^{(J)}(\alpha ,\beta ,\gamma )]^{*}\mathbf {Y} _{JM'}^{(s)}(\theta ,\varphi ),}
При инверсии электрические и продольные сферические гармоники ведут себя так же, как и скалярные сферические функции, т.е.
I
^
N
J
M
(
θ
,
φ
)
=
(
−
1
)
J
N
J
M
(
θ
,
φ
)
,
{\displaystyle {\hat {I}}\mathbf {N} _{JM}(\theta ,\varphi )=(-1)^{J}\mathbf {N} _{JM}(\theta ,\varphi ),}
I
^
M
J
M
(
θ
,
φ
)
=
(
−
1
)
J
+
1
M
J
M
(
θ
,
φ
)
,
{\displaystyle {\hat {I}}\mathbf {M} _{JM}(\theta ,\varphi )=(-1)^{J+1}\mathbf {M} _{JM}(\theta ,\varphi ),}
При расчете закона Стокса для сопротивления, которое вязкая жидкость оказывает на небольшую сферическую частицу, распределение скорости подчиняется уравнениям Навье -Стокса, пренебрегая инерцией, т. Е.
0
=
∇
⋅
v
,
0
=
−
∇
p
+
η
∇
2
v
,
{\displaystyle {\begin{aligned}0&=\nabla \cdot \mathbf {v} ,\\\mathbf {0} &=-\nabla p+\eta \nabla ^{2}\mathbf {v} ,\end{aligned}}}
с граничными условиями
v
=
{
0
r
=
a
,
−
U
0
r
→
∞
.
{\displaystyle \mathbf {v} ={\begin{cases}\mathbf {0} &r=a,\\-\mathbf {U} _{0}&r\to \infty .\end{cases}}}
где u - это относительная скорость частицы к жидкости далеко от частицы. В сферических координатах эта скорость в бесконечности может быть написана как
U
0
=
U
0
(
cos
θ
r
^
−
sin
θ
θ
^
)
=
U
0
(
Y
10
+
Ψ
10
)
.
{\displaystyle \mathbf {U} _{0}=U_{0}\left(\cos \theta \,{\hat {\mathbf {r} }}-\sin \theta \,{\hat {\mathbf {\theta } }}\right)=U_{0}\left(\mathbf {Y} _{10}+\mathbf {\Psi } _{10}\right).}
Последнее выражение предполагает расширение в сферических гармониках для скорости жидкости и давления
p
=
p
(
r
)
Y
10
,
v
=
v
r
(
r
)
Y
10
+
v
(
1
)
(
r
)
Ψ
10
.
{\displaystyle {\begin{aligned}p&=p(r)Y_{10},\\\mathbf {v} &=v^{r}(r)\mathbf {Y} _{10}+v^{(1)}(r)\mathbf {\Psi } _{10}.\end{aligned}}}
Замена в уравнениях Navier -Stokes создает набор обычных дифференциальных уравнений для коэффициентов.
Здесь используются следующие определения:
Y
e
m
n
=
cos
m
φ
P
n
m
(
cos
θ
)
Y
o
m
n
=
sin
m
φ
P
n
m
(
cos
θ
)
{\displaystyle {\begin{aligned}Y_{emn}&=\cos m\varphi P_{n}^{m}(\cos \theta )\\Y_{omn}&=\sin m\varphi P_{n}^{m}(\cos \theta )\end{aligned}}}
X
o
e
m
n
(
k
k
)
=
∇
×
(
k
Y
e
o
m
n
(
k
k
)
)
{\displaystyle \mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)=\nabla \times \left(\mathbf {k} Y_{^{o}_{e}mn}\left({\frac {\mathbf {k} }{k}}\right)\right)}
Z
e
o
m
n
(
k
k
)
=
i
k
k
×
X
o
e
m
n
(
k
k
)
{\displaystyle \mathbf {Z} _{^{o}_{e}mn}\left({\frac {\mathbf {k} }{k}}\right)=i{\frac {\mathbf {k} }{k}}\times \mathbf {X} _{^{e}_{o}mn}\left({\frac {\mathbf {k} }{k}}\right)}
z
n
{\displaystyle z_{n}}
функции Бесселя , с помощью расширения плоской волны, можно получить следующие интегральные отношения: [ 11 ]
N
p
m
n
(
1
)
(
k
,
r
)
=
i
−
n
4
π
∫
Z
p
m
n
(
k
k
)
e
i
k
⋅
r
d
Ω
k
{\displaystyle \mathbf {N} _{pmn}^{(1)}(k,\mathbf {r} )={\frac {i^{-n}}{4\pi }}\int \mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)e^{i\mathbf {k} \cdot \mathbf {r} }d\Omega _{k}}
M
p
m
n
(
1
)
(
k
,
r
)
=
i
−
n
4
π
∫
X
p
m
n
(
k
k
)
e
i
k
⋅
r
d
Ω
k
{\displaystyle \mathbf {M} _{pmn}^{(1)}(k,\mathbf {r} )={\frac {i^{-n}}{4\pi }}\int \mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)e^{i\mathbf {k} \cdot \mathbf {r} }d\Omega _{k}}
В случае, когда
z
n
{\displaystyle z_{n}}
[ 12 ] [ 11 ]
M
p
m
n
(
3
)
(
k
,
r
)
=
i
−
n
2
π
k
∬
−
∞
∞
d
k
‖
e
i
(
k
x
x
+
k
y
y
±
k
z
z
)
k
z
X
p
m
n
(
k
k
)
{\displaystyle \mathbf {M} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _{-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{k_{z}}}\mathbf {X} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)}
N
p
m
n
(
3
)
(
k
,
r
)
=
i
−
n
2
π
k
∬
−
∞
∞
d
k
‖
e
i
(
k
x
x
+
k
y
y
±
k
z
z
)
k
z
Z
p
m
n
(
k
k
)
{\displaystyle \mathbf {N} _{pmn}^{(3)}(k,\mathbf {r} )={\frac {i^{-n}}{2\pi k}}\iint _{-\infty }^{\infty }dk_{\|}{\frac {e^{i\left(k_{x}x+k_{y}y\pm k_{z}z\right)}}{k_{z}}}\mathbf {Z} _{pmn}\left({\frac {\mathbf {k} }{k}}\right)}
k
z
=
k
2
−
k
x
2
−
k
y
2
{\textstyle k_{z}={\sqrt {k^{2}-k_{x}^{2}-k_{y}^{2}}}}
(
3
)
{\displaystyle (3)}
^ Баррера, RG; Эстевес, Джорджия; Giraldo, J (1985-10-01). «Векторные сферические гармоники и их применение к магнитостатике». Европейский журнал физики . 6 (4). IOP Publishing: 287–294. Bibcode : 1985ejph .... 6..287b . Citeseerx 10.1.1.718.2001 doi : 10.1088/0143-0807/6/4/014 . ISSN 0143-0807 . S2CID 250894245 . ^ Карраскал, б; Эстевес, Джорджия; Ли, Пейлиан; Лоренцо В. (1991-07-01). «Векторные сферические гармоники и их применение к классической электродинамике». Европейский журнал физики . 12 (4). IOP Publishing: 184–191. Bibcode : 1991ejph ... 12..184c . doi : 10.1088/0143-0807/12/4/007 . ISSN 0143-0807 . S2CID 250886412 . ^ Хилл, Эл (1954). «Теория векторных сферических гармоник» (PDF) . Американский журнал физики . 22 (4). Американская ассоциация учителей физики (AAPT): 211–214. Bibcode : 19544mjph..22..211h . doi : 10.1119/1.1933682 . ISSN 0002-9505 . S2CID 124182424 . Архивировано из оригинала (PDF) 2020-04-12. ^ Вайнберг, Эрик Дж. (1994-01-15). «Монопольный вектор сферический гармоник». Физический обзор d . 49 (2). Американское физическое общество (APS): 1086–1092. arxiv : hep-th/9308054 BIBCODE : 1994PHRVD..49.1086W . doi : 10.1103/physrevd.49.1086 . ISSN 0556-2821 . PMID 10017069 . S2CID 6429605 . ^ PM Morse и H. Feshbach, Методы теоретической физики, часть II , Нью-Йорк: McGraw-Hill, 1898-1901 (1953)
^ Бохрен, Крейг Ф. и Дональд Р. Хаффман, Поглощение и рассеяние света с помощью мелких частиц, Нью -Йорк: Wiley, 1998, 530 стр., ISBN 0-471-29340-7 , ISBN 978-0-471-29340-8 (второе издание)
^ Подпрыгнуть до: а беременный Страттон, JA (1941). Электромагнитная теория ^ D. A. Varhalovich, A. N. Moskalev, and V. K. Khersonskii, Quantum Theory of Angular Momentum [in Russian], Nauka, Leningrad (1975)
^ Чжан, Хуайонг; Хан, Йипинг (2008). «Теорема с добавлением для сферических векторных волновых функций и ее применение к коэффициентам формы луча». J. Opt. Соц Являюсь. Беременный 25 (2): 255–260. Bibcode : 2008 Josab..25..255z . doi : 10.1364/josab.25.000255 . ^ Stein, Seymour (1961). «Теоремы о добавлении для сферических волновых функций». Ежеквартально прикладной математики . 19 (1): 15–24. doi : 10.1090/QAM/120407 . ^ Подпрыгнуть до: а беременный Стаут, Б. (2012). Попов, E (ред.). «Сферическая гармоническая решетчатая сумма для решений» (PDF) . Институт Френнел, Университет Д'Айкс-Марсеил 6. Решетки: теория и числовые приложения. ^ Виттманн, RC (1988). «Сферические волновые операторы и формулы перевода» . IEEE транзакции по антеннам и распространению . 36 (8): 1078–1087. Bibcode : 1988tap ... 36.1078W . doi : 10.1109/8.7220 . 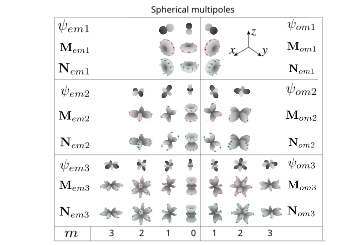





































































![{\displaystyle {\begin{aligned}{\mathbf {N} _{emn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\cos(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }}\\{{}+\cos(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{{}-m\sin(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8331b5c5a9b7381413a4230f6dd294ea6e29ddca)
![{\displaystyle {\begin{aligned}\mathbf {N} _{omn}(k,\mathbf {r} )=\qquad {\frac {z_{n}(\rho )}{\rho }}\sin(m\varphi )n(n+1)P_{n}^{m}(\cos(\theta ))\mathbf {e} _{\mathbf {r} }\\{}+\sin(m\varphi ){\frac {dP_{n}^{m}(\cos(\theta ))}{d\theta }}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\theta }\\{}+{m\cos(m\varphi ){\frac {P_{n}^{m}(\cos(\theta ))}{\sin(\theta )}}}{\frac {1}{\rho }}{\frac {d}{d\rho }}\left[\rho z_{n}(\rho )\right]\mathbf {e} _{\varphi }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d56063fb7f9fabaf20e04730bd1eeaf79296847)


![{\displaystyle {\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {L} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}k^{2}\left\{n\left[z_{n-1}(kr)\right]^{2}+(n+1)\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {M} _{^{e}_{o}mn}\cdot \mathbf {M} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{2n+1}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left[z_{n}(kr)\right]^{2}\\[3pt]\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {N} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)\left\{(n+1)\left[z_{n-1}(kr)\right]^{2}+n\left[z_{n+1}(kr)\right]^{2}\right\}\\[3pt]\int _{0}^{\pi }\int _{0}^{2\pi }\mathbf {L} _{^{e}_{o}mn}\cdot \mathbf {N} _{^{e}_{o}mn}\sin \vartheta d\vartheta d\varphi &=(1+\delta _{m,0}){\frac {2\pi }{(2n+1)^{2}}}{\frac {(n+m)!}{(n-m)!}}n(n+1)k\left\{\left[z_{n-1}(kr)\right]^{2}-\left[z_{n+1}(kr)\right]^{2}\right\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f3423865810fc65f5eb7bc80cfd88e8c9c9f16b)
![{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )\mathbf {Y} _{JM}^{(s)}(\theta ,\varphi )=\sum _{M'=-J}^{J}[D_{MM'}^{(J)}(\alpha ,\beta ,\gamma )]^{*}\mathbf {Y} _{JM'}^{(s)}(\theta ,\varphi ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95badc97e00d533b5a7ba1dba9d762bfb9bcaca2)















