Нонограмма

Эта статья о головоломке. Чтобы узнать о звездообразном многоугольнике, см. Nonagram . О вычислительном устройстве см. Номограмма .

«Пикросс» перенаправляется сюда. Чтобы узнать о серии видеоигр, разработанной Jupiter, см. Picross e и Picross S.

Заполненная нонограмма буквы «W» из логотипа Википедии.

Нонограммы , также известные как Hanjie , Paint by Numbers , Picross , Griddlers и Pic-a-Pix, представляют собой логические головоломки с картинками , в которых ячейки в сетке необходимо раскрасить или оставить пустыми в соответствии с числами на краях сетки, чтобы раскрыть скрытую информацию. картина. В этой головоломке числа представляют собой форму дискретной томографии , которая измеряет, сколько непрерывных линий заполненных квадратов имеется в любой строке или столбце. Например, подсказка «4 8 3» будет означать, что существуют наборы из четырех, восьми и трех заполненных квадратов в этом порядке, по крайней мере с одним пустым квадратом между последовательными наборами.

Эти головоломки часто черно-белые, описывающие двоичное изображение , но их также можно раскрасить. Если они цветные, числовые подсказки также окрашиваются, чтобы указать цвет квадратов. Два числа разного цвета могут иметь или не иметь между собой пробел. Например, черная четверка, за которой следует красная двойка, может означать четыре черных ящика, несколько пустых мест и два красных ящика, или это может просто означать четыре черных ящика, за которыми сразу следуют два красных. Нонограммы не имеют теоретических ограничений по размеру и не ограничиваются квадратными макетами.

Нонограммы были названы в честь Нон Исиды, одного из двух изобретателей головоломки.

Имена

Нонограммы также известны под многими другими названиями, в том числе «головоломка Ханцзе», «Раскраска по номерам», «Раскраска по номерам». Кросспикс, Гриддлеры, Пик-а-Пикс, Пикросс, Picma, PrismaPixels, Пиксельные головоломки, Crucipixel, Edel,FigurePic, Hanjie, HeroGlyphix, Illust-Logic, Японские кроссворды, Японские головоломки, Каре Карала!, Logic Art, Logic Square, Logicolor, Logik-Puzzles, Logimage, Oekaki Logic, Логика рисования, логика изображений, цунами, рисование судоку, логические головоломки, формирующие картинки, и бинарные раскраски.

История

В 1987 году Нон Исида, японский графический редактор, выиграл конкурс в Токио, разработав сетчатые изображения с использованием включенных и выключенных огней небоскребов. Это привело ее к идее головоломки, основанной на заполнении определенных квадратов сетки. По совпадению, профессиональный японский решатель головоломок по имени Тэцуя Нисио самостоятельно придумал те же головоломки и опубликовал их в другом журнале. В то время нонограммы также называли логическими головоломками, образующими картинки.

Печатное издание

В 1988 году компания Non Ishida опубликовала в Японии три головоломки с сеткой с картинками под названием «Пазлы для оконного искусства». В 1990 году Джеймс Далгети в Великобритании придумал название «Нонограммы» в честь Нона Исиды. и The Sunday Telegraph начали публиковать их еженедельно. К 1993 году первая книга нонограмм была опубликована издательством Нон Исида в Японии. Газета Sunday Telegraph опубликовала специальную книгу-головоломку под названием «Книга нонограмм». Нонограммы также публиковались в Швеции и США (первоначально Games ). журналом ), Южная Африка и другие страны. В 1998 году газета Sunday Telegraph провела конкурс на выбор нового названия для своих головоломок. Griddlers стало победным именем, которое выбрали читатели. В 1993 году Исида опубликовал «Книгу нонограмм».

Электронные пазлы

К 1995 году головоломки с раскраской по номерам были реализованы на ручных электронных игрушках, таких как Game Boy, и на других пластиковых игрушках-головоломках. Nintendo подхватила это увлечение головоломками и выпустила две игры Picross (кроссворды с картинками) для Game Boy и девять для Super Famicom (восемь из которых были выпущены с двухмесячными интервалами для Nintendo Power Super Famicom Cartridge Writer под названием NP). сериал) в Японии. Только одна из них, Mario's Picross для Game Boy, была выпущена за пределами Японии. С тех пор одним из самых плодовитых разработчиков игр Picross стала компания Jupiter Corporation , выпустившая Picross DS для Nintendo DS в 2007 году, 8 игр серии Picross e для интернет-магазина Nintendo 3DS (а также 5 игр для конкретных персонажей, в том числе с участием персонажей Pokémon , Zelda и Sanrio ) и 9 игр серии Picross S для Nintendo Switch (вместе с двумя играми, посвященными конкретным персонажам, с участием Kemono Friends и Overlord соответственно, а также еще одной игрой с интеллектуальной собственностью SEGA). « Мастер-система и Бытие» ).

Возросшая популярность в Японии привела к появлению новых издателей, и к настоящему времени появилось несколько ежемесячных журналов, некоторые из которых содержали до 100 головоломок. Японская аркадная игра Logic Pro была выпущена Deniam Corp в 1996 году, а в следующем году было выпущено продолжение. Британский разработчик игр Jagex выпустил головоломку с нонограммами в 2011 году в рамках ежегодного Хэллоуинского мероприятия для своей ролевой игры Runescape . В 2013 году компания Casual Labs выпустила мобильную версию этих головоломок под названием Paint it Back, посвященную восстановлению художественной галереи. Выпущенная в начале 2017 года, Pictopix была представлена ​​как достойный наследник Picross для ПК от Rock, Paper, Shotgun. В частности, игра позволяет игрокам делиться своими творениями.

Сегодня

«Раскраски по номерам» были опубликованы издательствами Sanoma Uitgevers в Нидерландах, Puzzler Media (ранее British European Associated Publishers) в Великобритании и Nikui Rosh Puzzles в Израиле. Журналы с задачками-нонограммами издаются в США, Великобритании, Германии, Нидерландах, Италии, Венгрии, Финляндии, Чехии, Словакии, России, Украине и многих других странах.

Пример

пустая нонограмма 2 2 0 9 9 2 2 4 4 0 0 4 6 2 2 2 2 6 4 2 2 2 0

решена нонограмма 2 2 0 9 9 2 2 4 4 0 0 4 6 2 2 2 2 6 4 2 2 2 0

Методы решения

Пример решения головоломки с нонограммами с использованием крестиков для обозначения логически подтвержденных пробелов. Некоторые этапы процесса сгруппированы вместе.

Чтобы решить головоломку, нужно определить, какие ячейки будут ящиками, а какие пустыми. Решатели часто используют точку или крестик для обозначения ячеек, в которых они уверены, что они являются пробелами. Ячейки, которые можно определить логически, должны быть заполнены. Если используется угадывание, одна ошибка может распространиться на все поле и полностью испортить решение. Ошибка иногда выходит на поверхность только через некоторое время, когда исправить головоломку очень сложно. Скрытая картинка может помочь найти и устранить ошибку, но в остальном она играет мало роли в процессе решения, так как может ввести в заблуждение.

Многие головоломки можно решить, рассуждая только об одной строке или столбце за раз, затем пробуя другую строку или столбец и повторяя это до тех пор, пока головоломка не будет завершена. Более сложные головоломки также могут потребовать нескольких типов вопросов «а что, если?» рассуждения, включающие более одной строки (или столбца). Это работает при поиске противоречий, например, когда ячейка не может быть рамкой, потому что какая-то другая ячейка выдаст ошибку, это должен быть пробел.

Простые коробки

В начале решения можно использовать простой метод, чтобы определить как можно больше ящиков. Этот метод использует соединения возможных мест для каждого блока ящиков. Например, в ряду из десяти ячеек только с одной подсказкой 8 связанный блок, состоящий из 8 ячеек, может распространяться из

• правая граница, оставляя два пробела слева;
• левая граница, оставляя справа два пробела;
• или где-то посередине.

В результате блок должен распространиться на шесть центральных ячеек строки.

То же самое происходит, когда в ряду больше подсказок. Например, в ряду из десяти ячеек с подсказками 4 и 3 связанные блоки коробок могут быть

• толпились слева, один рядом с другим, оставляя два места справа;
• толпились справа, один рядом с другим, оставляя два места слева;
• или где-то между.

Следовательно, первый блок из четырех ячеек заведомо включает в себя третью и четвертую ячейки, а второй блок из трех ячеек обязательно включает восьмую ячейку. Таким образом, ящики можно размещать в третьей, четвертой и восьмой ячейках. При определении блоков таким способом блоки можно размещать в ячейках только при одного и того же блока перекрытии ; в этом примере в шестой ячейке есть перекрытие, но оно из разных блоков, поэтому пока нельзя сказать, будет ли шестая ячейка содержать блок.

Простые пространства

Этот метод заключается в определении пробелов путем поиска ячеек, находящихся за пределами возможных блоков блоков. Например, если рассматривать ряд из десяти ячеек с квадратами в четвертой и девятой ячейке и с подсказками 3 и 1 , блок, привязанный к подсказке 3, распространится через четвертую ячейку, а подсказка 1 будет в девятой ячейке.

Во-первых, подсказка 1 завершена, и на каждой стороне связанного блока будет пробел.

Во-вторых, подсказка 3 может распространяться только где-то между второй и шестой клеткой, потому что она всегда должна включать четвертую ячейку; однако при этом могут остаться ячейки, которые в любом случае не могут быть клетками, т. е. первая и седьмая.

Примечание. В этом примере учитываются все блоки; это не всегда так. Игрок должен быть осторожен, так как могут быть подсказки или блоки, которые еще не связаны друг с другом.

Принуждение

В этом методе будет показано значение пробелов. Пространство, расположенное где-то в середине незавершенного ряда, может заставить большой блок сдвинуться в ту или иную сторону. Кроме того, пробел, который слишком мал для любого возможного блока, может быть заполнен пробелами.

Например, рассмотрим ряд из десяти ячеек с пробелами в пятой и седьмой ячейках и с подсказками 3 и 2 :

• подсказка числа 3 будет смещена влево, потому что она больше нигде не поместится.
• Пустой пробел в шестой ячейке слишком мал, чтобы вместить подсказки, такие как 2 или 3, и может быть заполнен пробелами.
• наконец, подсказка числа 2 распространится по девятой ячейке в соответствии с методом Simple Boxes, описанным выше.

Клей

Иногда рядом с границей есть коробка, которая находится от границы не дальше, чем на длину первой подсказки. В этом случае первая подсказка распространится через этот ящик и будет вытеснена за границу. В простейшем случае, когда в первой или последней ячейке строки или столбца присутствует прямоугольник, первая или последняя подсказка должна быть выровнена по краю этой строки или столбца.

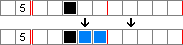
Учитывая ряд из десяти ячеек с рамкой в ​​третьей ячейке и подсказкой 5 , подсказка 5 всегда будет простираться от третьей до пятой клетки (но не обязательно до второй или шестой). Таким образом, можно пометить третью, четвертую и пятую ячейки как принадлежащие 5 .

Примечание. Этот метод также может работать в середине строки, дальше от границ.

• Пространство может действовать как граница, если первая подсказка находится справа от этого места.
• Первой . подсказке также могут предшествовать некоторые другие подсказки, если все подсказки уже привязаны к левой части форсирующего пространства

Соединение и разделение

Ближайшие друг к другу ящики иногда могут быть объединены в один блок или разделены пробелом на несколько блоков. Если есть два блока с пустой ячейкой между ними, эта ячейка будет:

• Пробел, если при соединении двух блоков рамкой получится слишком большой блок.
• В блоке, если разделить два блока пробелом, получится слишком маленький блок, в котором не останется достаточно свободных ячеек.

Например, рассмотрим ряд из пятнадцати ячеек с квадратами в третьей, четвертой, шестой, седьмой, одиннадцатой и тринадцатой ячейке и с подсказками 5 , 2 и 2 :

• Подсказка 5 объединит первые два блока по коробке в один большой блок, потому что на месте получится блок всего из 4 коробок, чего там недостаточно.
• Подсказки 2 разделят последние два блока пробелом, потому что из коробки получится блок из трех непрерывных блоков, что там недопустимо.

Примечание. подсказки 2 На иллюстрации также показано, как выполняются . Однако это не часть техники соединения и разделения , а техника склеивания , описанная выше.

Пунктуация

Чтобы решить головоломку, обычно также очень важно сразу же заключить каждый связанный или завершенный блок коробок, разделив пробелы, как описано в разделе « Метод простых пространств ». Точная расстановка знаков препинания обычно приводит к большему принуждению и может оказаться жизненно важной для завершения головоломки. Примечание. В приведенных выше примерах это сделано не только для простоты.

Меркурий

Меркурий — это частный случай техники Простых пространств . Его название происходит от того, как ртуть отходит от стенок контейнера.

Если в ряду есть клетка, которая находится на том же расстоянии от границы, что и длина первой подсказки, первой ячейкой будет пробел. Это потому, что первая подсказка не помещается слева от коробки. Ему придется распространиться через этот ящик, оставив первую ячейку позади. Более того, когда блок на самом деле представляет собой блок из нескольких блоков справа, в начале строки будет больше пробелов, что определяется путем многократного использования этого метода.

Противоречия

Некоторые более сложные головоломки также могут потребовать более сложных рассуждений. Когда все простые методы, описанные выше, исчерпаны, может помочь поиск противоречий . Для облегчения исправлений разумно использовать карандаш (или другой цвет). Процедура включает в себя:

1. Пытаемся превратить пустую ячейку в поле (или затем в пробел).
2. Используя все доступные методы, чтобы решить как можно больше задач.
3. Если будет обнаружена ошибка, проверенная ячейка точно не будет коробкой. Это будет пробел (или ящик, если пробовалось пространство).

В этом примере в первой строке пробуется поле, что приводит к появлению пробела в начале этой строки. Затем пространство вызывает блок в первом столбце, который приклеивается к блоку из трех блоков в четвертом ряду. Однако это неверно, поскольку в третьем столбце не допускается наличие полей, что приводит к выводу, что проверенная ячейка не должна быть полем, а значит, это должен быть пробел.

Проблема этого метода в том, что нет быстрого способа определить, какую пустую ячейку попробовать в первую очередь. Обычно только несколько ячеек приводят к прогрессу, а остальные заходят в тупик. Наиболее достойными клетками для начала могут быть:

• ячейки, имеющие много непустых соседей;
• ячейки, находящиеся близко к границам или близко к блокам пробелов;
• ячейки, находящиеся внутри строк, состоящих из большего количества непустых ячеек.

Математический подход

Можно начать собирать головоломку, используя математический метод заполнения блоков для строк/столбцов независимо от других строк/столбцов. Это хороший «первый шаг» и математический ярлык для методов, описанных выше. Процесс выглядит следующим образом:

1. Сложите подсказки вместе, плюс по 1 на каждое «пространство» между ними. Например, если подсказка — 6 2 3, на этом этапе получается сумма 6 + 1 + 2 + 1 + 3 = 13.
2. Вычтите это число из общего числа, доступного в строке (обычно это ширина или высота головоломки). Например, если подсказка на шаге 1 находится в строке шириной 15 ячеек, разница составит 15–13 = 2. Примечание. Если на левой или правой (верхней или нижней) границе можно использовать пробелы, это «сжимает» доступная площадь. Если известно, что крайняя правая клетка — пробел, то разница равна 14 — 13 = 1.
3. Для любых подсказок, число которых превышает число на шаге 2, некоторые блоки будут заполнены. В данном примере это относится к подсказкам 6 и 3, но не к 2.
4. Для каждой подсказки на шаге 3 вычтите число из шага 2, чтобы определить количество блоков, которые можно заполнить. Например, подсказка 6 будет содержать (6 - 2 =) 4 заполненных блока, а подсказка 3 будет иметь ( 3 - 2 =) 1. Примечание. При применении той же процедуры к подсказке, для которой «неудачный» шаг 3, будет получено неположительное число, указывающее, что для этой подсказки не будут заполнены никакие блоки. Подсказка 2 дает число (2 - 2 =) 0; если бы была подсказка 1, то получилось бы число (1 - 2 =) -1.
5. Чтобы заполнить блоки, предположим, что все блоки сдвинуты в одну сторону, посчитайте с этой стороны «через» блоки и засыпьте соответствующее количество блоков. Это можно сделать с любого направления. Например, подсказку 6 можно выполнить одним из двух способов:
   1. Слева: поскольку 6 — первое число, отсчитайте 6 блоков от левого края, заканчиваясь 6-м блоком. Теперь «заполните» 4 блока (число, полученное на шаге 4), чтобы ячейки с 3 по 6 были заполнены.
   2. Справа: начиная справа, необходимо учитывать подсказки, находящиеся справа от подсказки №6. Начиная с ячейки 15, отсчитайте 3 клетки для подсказки 3 (до ячейки 13), затем пробел (12), затем подсказку 2 (10), затем пробел (9), затем подсказку 6 (3). Из третьей ячейки «заполните» 4 блока, заполняя ячейки с 3 по 6. Результаты такие же, как если бы вы делали это слева на шаге выше.
6. Повторите шаг 5 для всех подсказок, указанных в шаге 3.

На иллюстрации в строке 1 показаны ячейки, заполненные в ходе этой процедуры, в строках 2 и 4 показано, как блоки сдвигаются в сторону на шаге 5, а в строках 3 и 5 показаны ячейки, заполненные обратно на шаге 5.

Использование этой техники для всех строк и столбцов в начале головоломки дает хороший старт для ее завершения. Примечание. Некоторые строки/столбцы изначально не дадут никаких результатов. Например, ряд из 20 ячеек с подсказкой 1 4 2 5 даст 1 + 1 + 4 + 1 + 2 + 1 + 5 = 15. 20 - 15 = 5. Ни одна из подсказок не превышает 5. Также , этот метод можно использовать в меньшем масштабе. Если в центре или по обеим сторонам есть свободные места, даже если определенные подсказки уже обнаружены, этот метод можно использовать с оставшимися подсказками и доступными местами.

Более глубокая рекурсия

Некоторые головоломки могут потребовать более глубокого поиска противоречий. Однако это невозможно сделать просто с помощью ручки и карандаша, поскольку необходимо искать множество возможностей. Этот метод удобен для использования на компьютере.

Несколько строк

В некоторых случаях рассуждения над набором строк также могут привести к следующему шагу решения даже без противоречий и более глубокой рекурсии. Однако найти такие множества обычно так же сложно, как и найти противоречия.

Нонограммы в вычислительной технике

Решение неграмматических головоломок является NP-полной задачей. Это означает, что не существует с полиномиальным временем алгоритма , который решает все неграмматические головоломки, если только P = NP .

Однако некоторые классы головоломок, например те, в которых каждая строка или столбец имеет только один блок ячеек и все ячейки соединены, можно решить за полиномиальное время, превратив задачу в случай 2-выполнимости .

Программные решатели

Подробное сравнение и обсуждение алгоритмов решения нонограмм можно найти на сайте WebPBN (Web Paint-By-Number). Решатель Nonogram, написанный на C++ и опубликованный в журнале Pattern Recognition, решает линии не более чем за квадратичное время .

Версии видеоигр

Nintendo опубликовала несколько видеоигр без грамматики под названием «Пикросс» ( ピクロス , Pikurosu ) . Игра Nintendo Game Boy для Mario's Picross была первоначально выпущена в Японии 14 марта 1995 года и имела приличный успех. Однако игре не удалось стать хитом на рынке США, несмотря на мощную рекламную кампанию со стороны Nintendo. Сложность игры возрастает: последовательные уровни головоломки содержат более крупные головоломки. У каждой головоломки есть ограниченное количество времени, которое нужно решить. Подсказки (очистка линии) могут быть запрошены в виде штрафа по времени, а за допущенные ошибки также начисляются штрафы по времени (сумма увеличивается за каждую ошибку). Picross 2 был выпущен позже для Game Boy, а Mario's Super Picross для Super Famicom, ни один из которых не был переведен для рынка США ( Mario's Super Picross однако Wii был позже выпущен в сервисе PAL виртуальной консоли 14 сентября 2007 г. , в рамках фестиваля Hanabi Festival , а также в сервисе Nintendo Switch Online по всему миру 23 сентября 2020 г. ). В обеих играх был представлен Пикросс Варио также был заклятый враг Марио , в роли которого . Эти раунды различаются удалением функции подсказки, а ошибки не наказываются - ценой того, что ошибки даже не раскрываются. Эти раунды можно пройти только тогда, когда отмечены все правильные поля без ошибок. Ограничение по времени также было снято. Nintendo также выпустила восемь томов Picross на японском периферийном устройстве Nintendo Power в Японии под названием NP Picross , каждый из которых содержит новый набор головоломок, включая головоломки, основанные на различных персонажах Nintendo, таких как Марио , The Legend of Zelda и Pokémon .

Nintendo выпустила Picross DS для портативной системы Nintendo DS в 2007 году. Он содержит несколько этапов различной сложности: от сеток 5x5 до сеток 25x20. Обычный режим сообщает игрокам, допустили ли они ошибку (со штрафом по времени), а свободный режим — нет. Перед началом головоломки во всех режимах доступна подсказка; игра случайным образом показывает полную строку и столбец. Дополнительные головоломки были доступны через Nintendo Wi-Fi Connection; Были доступны некоторые оригинальные головоломки Марио Пикросса. Однако 20 мая 2014 года сервис был закрыт. Nintendo выпускала новые выпуски раз в две недели. Picross DS был выпущен в Европе и Австралии 11 мая 2007 г. и в США 30 июля 2007 г. и был хорошо принят критиками, в том числе Крейгом Харрисом. Джессика Уодли и Дэйв Маккарти называя игру «захватывающей». 3D-версия игры под названием Picross 3D также была выпущена для DS в Японии в 2009 году и на международном уровне в 2010 году. Продолжение Picross 3D: Round 2 было выпущено для Nintendo 3DS в 2015 году. Еще одна загружаемая версия игры была выпущена для Nintendo eShop на Nintendo 3DS под названием Picross e , Picross e2 и Picross e3 , выпущенная в 2013 году, а Picross e4 была выпущена в 2014 году. 7 декабря 2015 года Nintendo также выпустила дополнительный доход Pokémon в виде бесплатной для игры Pokémon Picross Nintendo 3DS. My Nintendo Picross The Legend of Zelda: Twilight Princess была выпущена для Nintendo 3DS 31 марта 2016 года исключительно в качестве премиум-награды для My Nintendo .

Другие компании также выпустили видеоигры без грамматики, например Falcross. для iOS , Across-Stitch от Knitwit Studios для Microsoft Windows и Apple macOS , а также серию игр Color Cross от Little Worlds Studio для Nintendo DS, Microsoft Windows и iOS . Кроме того, головоломки с нонограммами появились в играх-головоломках, не связанных с пикроссом, например, в Deadly Rooms of Death пятой части , The Second Sky . В нем головоломки с нонограммами (снова называемые головоломками «Пикросс»), представляющие внутриигровые объекты, являются необязательными, открываемыми головоломками в конце игры, в которые можно играть на уровне «Центральный вокзал», и их решение открывает бонусные уровни в игре. В 2018 году Konami выпустила игру под названием Pixel Puzzle Collection или Picross Puzzle (ピクロジパズル), в которой представлены классические персонажи и спрайты Konami.

Другие логические головоломки с картинками

Раскраска пентамино по номерам — это вариант, в котором двенадцать фигур пентамино необходимо разместить в сетке, не касаясь друг друга (даже по диагонали).

Триддлеры являются ответвлением, в котором вместо квадратов используются треугольные формы.

Раскраска парами или Link-a-Pix состоит из сетки, в которой некоторые квадраты заполнены числами; пары чисел должны быть расположены правильно и соединены линией, заполняющей в общей сложности квадраты, равные этому числу. Есть только один уникальный способ соединить все квадраты в правильно составленную головоломку. По завершении квадраты с линиями заполняются; контраст с пустыми квадратами раскрывает картину. (Как указано выше, существуют цветные версии, в которых используются совпадающие числа одного и того же цвета.)

Fill-a-Pix также использует сетку с числами внутри. В этом формате каждое число указывает, сколько квадратов, непосредственно окружающих его и само себя, будет заполнено. Например, квадрат с пометкой «9» будет содержать все восемь окружающих квадратов и сам будет заполнен. Если он отмечен «0», все квадраты пусты.

Maze-a-Pix использует лабиринт в стандартной сетке. Когда найден единственный правильный маршрут от начала до конца, каждый «квадрат» решения заполняется (альтернативно заполняются все квадраты, не относящиеся к решению), чтобы создать картинку.

Tile Paint — еще один тип логической головоломки с картинками от Николи. Он работает как обычные нонограммы, за исключением того, что он указывает только общее количество квадратов в каждой строке или столбце, которые будут заполнены, а неправильные участки сетки имеют границы вокруг них, которые указывают, что, если один из квадратов внутри нее заполнен, все они должны быть заполнены.

См. также

• Линкор (головоломка)