Теорема о трёх геодезических
В дифференциальной геометрии теорема о трех геодезических , также известная как теорема Люстерника-Шнирельмана , утверждает, что каждое риманово многообразие с топологией сферы имеет по крайней мере три простых замкнутых геодезических (т.е. три вложенных геодезических круга). [1] Результат также может быть распространен на квазигеодезические на выпуклом многограннике и на замкнутые геодезические обратимых финслеровых 2-сфер. Теорема точна: хотя каждая риманова 2-сфера содержит бесконечное множество различных замкнутых геодезических, только три из них гарантированно не имеют самопересечений. Например, по результату Морса , если длины трёх главных осей эллипсоида различны, но достаточно близки друг к другу, то эллипсоид имеет только три простые замкнутые геодезические. [2]
История и доказательства
[ редактировать ]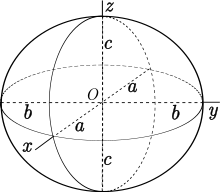
Геодезическая . на римановой поверхности — это кривая, локально прямая в каждой своей точке Например, на евклидовой плоскости геодезические — это линии , а на поверхности сферы геодезические — это большие круги . Кратчайший путь на поверхности между двумя точками всегда является геодезической, но могут существовать и другие геодезические. Геодезическая называется замкнутой геодезической , если она возвращается к своей начальной точке и исходному направлению; при этом он может перекреститься несколько раз. Теорема о трёх геодезических утверждает, что для поверхностей, гомеоморфных сфере, существуют по крайней мере три несамопересекающиеся замкнутые геодезические. Их может быть больше трех, например, в самой сфере их бесконечно много.
Этот результат вытекает из математики океанской навигации, где поверхность земли может быть точно смоделирована эллипсоидом , а также из изучения геодезических на эллипсоиде — кратчайших путях движения кораблей. В частности, почти сферический трехосный эллипсоид имеет только три простые замкнутые геодезические — экваторы. [3] В 1905 году Анри Пуанкаре предположил, что каждая гладкая поверхность, топологически эквивалентная сфере, также содержит по крайней мере три простые замкнутые геодезические: [4] а в 1929 году Лазарь Люстерник и Лев Шнирельманн опубликовали доказательство гипотезы; хотя общий топологический аргумент доказательства был верным, в нем использовался результат деформации, который позже оказался ошибочным. [5] Ряд авторов предложили неудовлетворительные решения проблемы. Общепринятое решение было предложено в 1980-х годах Грейсоном с помощью метода сокращения кривой потока. [6]
Обобщения
[ редактировать ]Усиленная версия теоремы утверждает, что на любой римановой поверхности, топологически являющейся сферой, обязательно существуют три простые замкнутые геодезические, длина которых не более чем пропорциональна диаметру поверхности. [7]
Число замкнутых геодезических длиной не более L на гладкой топологической сфере растет пропорционально L /log L , но не все такие геодезические могут быть гарантированно простыми. [8]
На компактных гиперболических римановых поверхностях существует бесконечно много простых замкнутых геодезических, но только конечное число с заданной границей длины. Они кодируются аналитически дзета-функцией Сельберга . Скорость роста количества простых замкнутых геодезических в зависимости от их длины исследовала Марьям Мирзахани . [9]
Существование трех простых замкнутых геодезических справедливо и для любой обратимой финслеровой метрики на 2-сфере. [10]
Негладкие метрики
[ редактировать ]Также возможно определить геодезические на некоторых поверхностях, которые не везде гладкие, например, на выпуклых многогранниках . Поверхность выпуклого многогранника имеет метрику, которая является локально евклидовой, за исключением вершин многогранника, а кривая, избегающая вершин многогранника, является геодезической, если она следует за отрезками прямых линий внутри каждой грани многогранника и остается прямой на каждом ребре многогранника. что оно пересекается. Хотя некоторые многогранники имеют простые замкнутые геодезические (например, у правильного тетраэдра и дисфеноидов бесконечно много замкнутых геодезических, и все они простые) [11] [12] другие этого не делают. В частности, простая замкнутая геодезическая выпуклого многогранника обязательно делит пополам общий угловой дефект вершин, а почти все многогранники не имеют таких биссектрис. [3] [11]
Тем не менее, теорему о трех геодезических можно распространить на выпуклые многогранники, рассматривая квазигеодезические, кривые, которые являются геодезическими, за исключением вершин многогранников, и имеют углы меньше π с обеих сторон в каждой вершине, которую они пересекают. Версия теоремы о трех геодезических для выпуклых многогранников утверждает, что все многогранники имеют по крайней мере три простых замкнутых квазигеодезических; это можно доказать, аппроксимировав многогранник гладкой поверхностью и применив к этой поверхности теорему о трех геодезических. [13] , остается открытым Вопрос о том, можно ли построить какую-либо из этих квазигеодезических за полиномиальное время . [14] [15]
Ссылки
[ редактировать ]- ^ Пуанкаре, Х. (1905), «Sur les lignes géodésiques des Surfaces convexes» [Геодезические линии на выпуклых поверхностях], Труды Американского математического общества (на французском языке), 6 (3): 237–274, doi : 10.2307/1986219 , JSTOR 1986219 .
- ^ Баллманн, В.: О длинах замкнутых геодезических линий на выпуклых поверхностях. Изобретать. Математика. 71, 593–597 (1983)
- ^ Jump up to: Перейти обратно: а б Гальперин, Г. (2003), «Выпуклые многогранники без простых замкнутых геодезических» (PDF) , Регулярная и хаотическая динамика , 8 (1): 45–58, Bibcode : 2003RCD.....8...45G , doi : 10.1070/RD2003v008n01ABEH000231 , МР 1963967 .
- ^ Пуанкаре, Х. (1905), «Sur les lignes géodésiques des Surfaces convexes» [Геодезические линии на выпуклых поверхностях], Труды Американского математического общества (на французском языке), 6 (3): 237–274, doi : 10.2307/1986219 , JSTOR 1986219 .
- ^ Люстерник, Л .; Шнирельманн, Л. (1929), «Проблема трех замкнутых геодезических на поверхностях рода 0» , Comptes Rendus de l'Académie des Sciences de Paris (на французском языке)), 189 : 269–271 .
- ^ Грейсон, Мэтью А. (1989), «Сокращение встроенных кривых» (PDF) , Annals of Mathematics , Second Series, 129 (1): 71–111, doi : 10.2307/1971486 , JSTOR 1971486 , MR 0979601 .
- ^ Лиокумович Евгений; Набутовский, Александр; Ротман, Регина (2017), «Длины трех простых периодических геодезических на римановой 2-сфере», Mathematische Annalen , 367 (1–2): 831–855, arXiv : 1410.8456 , Bibcode : 2014arXiv1410.8456L , doi : 10.1007/ s00208-016-1402-5 .
- ^ Хингстон, Нэнси (1993), «О росте числа замкнутых геодезических в двухсфере», International Mathematics Research Notes , 1993 (9): 253–262, doi : 10.1155/S1073792893000285 , MR 1240637 .
- ^ Мирзахани, Марьям (2008), «Рост числа простых замкнутых геодезических на гиперболических поверхностях», Анналы математики , 168 (1): 97–125, doi : 10.4007/annals.2008.168.97 , MR 2415399 , Zbl 1177.37036 ,
- ^ Де Филиппис, Гвидо ; Марини, Микеле; Маццучелли, Марко; Зур, Стефан (2022), «Замкнутые геодезические на обратимых финслеровых 2-сферах», Журнал теории и приложений с фиксированной точкой , 24 (2), arXiv : 2002.00415 , doi : 10.1007/s11784-022-00962-9 .
- ^ Jump up to: Перейти обратно: а б Фукс, Дмитрий [на немецком языке] ; Фукс, Екатерина (2007), «Замкнутые геодезические на правильных многогранниках» (PDF) , Московский математический журнал , 7 (2): 265–279, 350, doi : 10.17323/1609-4514-2007-7-2-265-279 , МР 2337883 .
- ^ Коттон, Эндрю; Фриман, Дэвид; Гнепп, Андрей; Нг, Тинг; Спивак, Джон; Йодер, Кара (2005), «Изопериметрическая проблема на некоторых сингулярных поверхностях», Журнал Австралийского математического общества , 78 (2): 167–197, doi : 10.1017/S1446788700008016 , MR 2141875 .
- ^ Погорелов, А.В. (1949), "Квазигеодезические линии на выпуклой поверхности" , Математический сборник , Н.С., 25 (67): 275–306, МР 0031767 .
- ^ Демейн, Эрик Д .; О'Рурк, Джозеф (2007), «24 геодезические: Люстерник – Шнирельман», Алгоритмы геометрического складывания: связи, оригами, многогранники , Кембридж: Cambridge University Press, стр. 372–375, doi : 10.1017/CBO9780511735172 , ISBN 978-0-521-71522-5 , МР 2354878 .
- ^ Ито, Джин-ичи; О'Рурк, Джозеф ; Вилку, Костин (2010), «Звездное развертывание выпуклых многогранников посредством квазигеодезических петель», Дискретная и вычислительная геометрия , 44 (1): 35–54, arXiv : 0707.4258 , doi : 10.1007/s00454-009-9223-x , MR 2639817 .