Шаблон Тьюринга

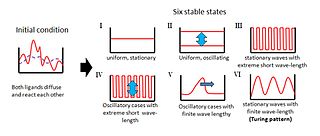
Паттерн Тьюринга — это концепция, введенная английским математиком Аланом Тьюрингом в статье 1952 года под названием « Химическая основа морфогенеза », которая описывает, как узоры в природе , такие как полосы и пятна, могут возникать естественным и автономным образом из однородного, однородного состояния. [1] [2] Эта картина возникает из-за неустойчивости Тьюринга , которая, в свою очередь, возникает из-за взаимодействия между дифференциальной диффузией (т.е. различными значениями коэффициентов диффузии) химических веществ и химической реакцией. Механизм нестабильности непредвиден, поскольку можно было бы ожидать, что чистый процесс диффузии окажет стабилизирующее влияние на систему.
Обзор
[ редактировать ]В своей статье [1] Тьюринг исследовал поведение системы, в которой два диффундирующих вещества взаимодействуют друг с другом, и обнаружил, что такая система способна генерировать пространственно-периодическую структуру даже при случайном или почти однородном начальном состоянии. [3] До открытия этого механизма неустойчивости, возникающей из-за неравных коэффициентов диффузии двух веществ, всегда предполагалось, что диффузионные эффекты оказывают стабилизирующее влияние на систему.
Тьюринг выдвинул гипотезу, что возникающие в результате волнообразные структуры являются химической основой морфогенеза . [3] Паттерн Тьюринга часто встречается в сочетании с другими паттернами: развитие конечностей позвоночных является одним из многих фенотипов, демонстрирующих паттерн Тьюринга, перекрывающийся с дополнительным паттерном (в данном случае моделью французского флага ). [4]
До Тьюринга Яков Зельдович в 1944 году открыл этот механизм неустойчивости в связи с ячеистыми структурами, наблюдаемыми в пламени бедного водорода . [5] Зельдович объяснил клеточную структуру тем, что коэффициент диффузии водорода больше, чем коэффициент термодиффузии . В литературе по горению неустойчивость Тьюринга называется диффузионно-тепловой неустойчивостью .
Концепция
[ редактировать ]

Оригинальная теория, теория реакции-диффузии морфогенеза, послужила важной моделью в теоретической биологии . [6] Системы реакции-диффузии вызвали большой интерес как прототип модели формирования структур . Такие узоры, как фронты , шестиугольники , спирали , полосы и диссипативные солитоны , обнаруживаются как решения тьюринговских уравнений реакции-диффузии . [7]
Тьюринг предложил модель, в которой два однородно распределенных вещества (P и S) взаимодействуют, создавая стабильные структуры во время морфогенеза. Эти закономерности отражают региональные различия в концентрациях двух веществ. Их взаимодействие могло бы создать упорядоченную структуру из случайного хаоса. [8]
В модели Тьюринга вещество P способствует производству большего количества вещества P, а также вещества S. Однако вещество S подавляет производство вещества P; если S диффундирует легче, чем P, для вещества P будут генерироваться резкие волны разницы концентраций. Важной особенностью модели Тьюринга является то, что определенные длины волн в распределении веществ будут усиливаться, в то время как другие длины волн будут подавляться. [8]
Параметры зависят от рассматриваемой физической системы. В контексте пигментации кожи рыб соответствующее уравнение представляет собой трехпольное уравнение реакции-диффузии, в котором линейные параметры связаны с концентрацией пигментных клеток, а параметры диффузии не одинаковы для всех полей. [9] , легированных красителями В жидких кристаллах , процесс фотоизомеризации в жидкокристаллической матрице описывается уравнением реакции-диффузии двух полей (параметра порядка жидкого кристалла и концентрации цис-изомера азокрасителя). [10] Системы имеют очень разные физические механизмы химических реакций и диффузионного процесса, но на феноменологическом уровне обе имеют одни и те же ингредиенты.
Также было продемонстрировано, что паттерны Тьюринга возникают в развивающихся организмах без классической потребности в диффузионных морфогенах. Исследования эмбрионального развития кур и мышей подтверждают, что паттерны предшественников перьев и волосяных фолликулов могут формироваться без препаттерна морфогена, а вместо этого генерируются посредством самоагрегации мезенхимальных клеток, лежащих под кожей. [11] [12] В этих случаях однородная популяция клеток может образовывать агрегаты с регулярным рисунком, которые зависят от механических свойств самих клеток и жесткости окружающей внеклеточной среды. Регулярные закономерности клеточных агрегатов такого типа были первоначально предложены в теоретической модели, сформулированной Джорджем Остером, который постулировал, что изменения в подвижности и жесткости клеток могут привести к различным самовозникающим паттернам из однородного поля клеток. [13] Этот способ формирования паттернов может действовать в тандеме с классическими системами реакции-диффузии или независимо, создавая паттерны биологического развития.
Паттерны Тьюринга также могут быть ответственны за формирование отпечатков пальцев человека . [14]
Так же, как и в биологических организмах, закономерности Тьюринга встречаются и в других природных системах — например, узоры ветра, образующиеся в песке, повторяющаяся рябь атомного масштаба, которая может образовываться во время роста кристаллов висмута, и неравномерное распределение материи в галактическом диске . [15] [16] Хотя идеи Тьюринга о морфогенезе и паттернах Тьюринга оставались бездействующими в течение многих лет, сейчас они вдохновляют многие исследования в математической биологии . [17] Это основная теория биологии развития ; Важность модели Тьюринга очевидна, поскольку она дает ответ на фундаментальный вопрос морфогенеза: «как генерируется пространственная информация в организмах?». [3]
Паттерны Тьюринга также могут быть созданы в нелинейной оптике, как демонстрирует уравнение Луджиато-Лефевера .
Биологическое применение
[ редактировать ]
Механизм, который привлекает все большее внимание как генератор пятен и полос в системах развития, связан с процессом химической реакции-диффузии, описанным Тьюрингом в 1952 году. Это было схематизировано в виде биологической «локальной аутоактивации-латерального торможения». (LALI) структура Мейнхардта и Гирера. [19] Системы LALI, хотя формально похожи на реакционно-диффузионные системы, более подходят для биологических применений, поскольку они включают случаи, когда активатор и ингибитор опосредованы клеточными «реакторами», а не простыми химическими реакциями. [20] а пространственный транспорт может быть опосредован не только простой диффузией, но и другими механизмами. [21] Эти модели могут быть применены, среди прочего, к формированию конечностей и развитию зубов.
Модели реакции-диффузии можно использовать для прогнозирования точного местоположения бугорков зубов у мышей и полевок на основе различий в моделях экспрессии генов. [8] Модель может быть использована для объяснения различий в экспрессии генов между мышами и зубами полевки, сигнальным центром зуба, эмалевым узлом, секретами BMP, FGF и Shh. Shh и FGF ингибируют выработку BMP, тогда как BMP стимулирует как выработку большего количества BMP, так и синтез собственных ингибиторов. BMP также индуцируют дифференцировку эпителия, тогда как FGFs индуцируют рост эпителия. [22] В результате получается образец активности генов, который меняется по мере изменения формы зуба, и наоборот. Согласно этой модели, большие различия между молярами мышей и полевок могут быть вызваны небольшими изменениями в константах связывания и скоростях диффузии белков BMP и Shh. Небольшого увеличения скорости диффузии BMP4 и более сильной константы связывания его ингибитора достаточно, чтобы изменить характер роста зубов полевок на мышиный. [22] [23]
Эксперименты с проращиванием семян чиа , посаженных в лотки, подтвердили математическую модель Тьюринга. [24]
См. также
[ редактировать ]- Эволюционная биология развития
- Математическая и теоретическая биология
- Узоры в природе
- Реакционно-диффузионная система
- Спонтанное нарушение симметрии
- Вермикуляция
Ссылки
[ редактировать ]- ^ Jump up to: а б Тьюринг, Алан (1952). «Химические основы морфогенеза» (PDF) . Философские труды Лондонского королевского общества Б. 237 (641): 37–72. Бибкод : 1952РСПТБ.237...37Т . дои : 10.1098/rstb.1952.0012 . JSTOR 92463 . S2CID 120437796 .
- ^ Стюарт, Ян (1998). Другая тайна жизни: новая математика живого мира . Аллен Лейн : The Penguin Press . стр. 138–140, 142–146, 148, 149, 151, 152. ISBN. 0-713-99161-5 .
- ^ Jump up to: а б с Кондо, Сигэру (7 февраля 2017 г.). «Обновленная модель Тьюринга на основе ядра для изучения механизмов формирования биологических закономерностей» . Журнал теоретической биологии . 414 : 120–127. Бибкод : 2017JThBi.414..120K . дои : 10.1016/j.jtbi.2016.11.003 . ISSN 0022-5193 . ПМИД 27838459 .
- ^ Шарп, Джеймс; Грин, Джереми (2015). «Позиционная информация и реакция-диффузия: сочетание двух больших идей в биологии развития» . Разработка . 142 (7): 1203–1211. дои : 10.1242/dev.114991 . hdl : 10230/25028 . ПМИД 25804733 .
- ^ Зельдович, Ю.Б. (1944). Теория горения и детонации газов. Избранные труды Якова Борисовича Зельдовича, том I: Химическая физика и гидродинамика (с. 162-232). Принстон: Издательство Принстонского университета
- ^ Харрисон, LG (1993). «Кинетическая теория живого образа». Стараться . 18 (4). Издательство Кембриджского университета : 130–6. дои : 10.1016/0160-9327(95)90520-5 . ПМИД 7851310 .
- ^ Кондо, С.; Миура, Т. (23 сентября 2010 г.). «Модель реакции-диффузии как основа для понимания формирования биологических закономерностей». Наука . 329 (5999): 1616–1620. Бибкод : 2010Sci...329.1616K . дои : 10.1126/science.1179047 . ПМИД 20929839 . S2CID 10194433 .
- ^ Jump up to: а б с Гилберт, Скотт Ф., 1949- (2014). Биология развития (Десятое изд.). Сандерленд, Массачусетс, США. ISBN 978-0-87893-978-7 . OCLC 837923468 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) CS1 maint: несколько имен: список авторов ( ссылка ) CS1 maint: числовые имена: список авторов ( ссылка ) - ^ Накамасу, А.; Такахаши, Г.; Канбе, А.; Кондо, С. (11 мая 2009 г.). «Взаимодействия между пигментными клетками рыбок данио, ответственными за генерацию паттернов Тьюринга» . Труды Национальной академии наук . 106 (21): 8429–8434. Бибкод : 2009PNAS..106.8429N . дои : 10.1073/pnas.0808622106 . ПМК 2689028 . ПМИД 19433782 .
- ^ Андраде-Сильва, Игнасио; Бортолоццо, Умберто; Клерк, Марсель Г.; Гонсалес-Кортес, Грегорио; Резидори, Стефания ; Уилсон, Марио (27 августа 2018 г.). «Спонтанные светоиндуцированные узоры Тьюринга в скрученном нематическом слое, легированном красителем» . Научные отчеты . 8 (1): 12867. Бибкод : 2018NatSR...812867A . дои : 10.1038/s41598-018-31206-x . ПМК 6110868 . ПМИД 30150701 .
- ^ Гловер, Джеймс Д.; Уэллс, Кирсти Л.; Маттеус, Франциска; Художник Кевин Дж.; Хо, Уильям; Ридделл, Джон; Йоханссон, Жанетт А.; Форд, Мэтью Дж.; Яхода, Колин AB; Клика, Вацлав; Морт, Ричард Л. (2017). «Режимы иерархического формирования паттерна управляют морфогенезом волосяных фолликулов» . ПЛОС Биология . 15 (7): e2002117. дои : 10.1371/journal.pbio.2002117 . ПМК 5507405 . ПМИД 28700594 .
- ^ Шайер, Эми Э.; Родригес, Алан Р.; Шредер, Грант Г.; Кассианиду, Елена; Кумар, Санджай; Харланд, Ричард М. (2017). «Эмерджентная клеточная самоорганизация и механочувствительность инициируют структуру фолликулов в коже птиц» . Наука . 357 (6353): 811–815. дои : 10.1126/science.aai7868 . ПМЦ 5605277 . ПМИД 28705989 .
- ^ Остер, ГФ; Мюррей, доктор юридических наук; Харрис, АК (1983). «Механические аспекты мезенхимального морфогенеза». Журнал эмбриологии и экспериментальной морфологии . 78 : 83–125. ПМИД 6663234 .
- ^ Гейнс, Джеймс М. «Наконец, ученые раскрывают генетическую основу отпечатков пальцев» . Ученый . Проверено 27 февраля 2023 г.
- ^ Фусея, Юки; Кацуно, Хироясу; Бениа, Кямран; Капитульник, Аарон (8 июля 2021 г.). «Наномасштабные узоры Тьюринга в монослое висмута» . Физика природы . 17 (9): 1031–1036. arXiv : 2104.01058 . Бибкод : 2021NatPh..17.1031F . дои : 10.1038/s41567-021-01288-y . ISSN 1745-2481 . S2CID 237767233 .
- ^ Смолин, Ли (3 декабря 1996 г.). «Галактические диски как реакционно-диффузионные системы». arXiv : astro-ph/9612033 .
- ^ Вулли, Т.Э., Бейкер, Р.Э. , Майни, П.К. , Глава 34, Теория морфогенеза Тьюринга . В Коупленд, Б. Джек ; Боуэн, Джонатан П .; Уилсон, Робин ; Спревак, Марк (2017). Руководство Тьюринга . Издательство Оксфордского университета . ISBN 978-0198747826 .
- ^ Чжу, Цзяньфэн; Чжан, Юн-Тао; Альбер, Марк С.; Ньюман, Стюарт А. (28 мая 2010 г.). Исалан, Марк (ред.). «Формирование структуры голых костей: основная регуляторная сеть различной геометрии воспроизводит основные особенности развития и эволюции конечностей позвоночных» . ПЛОС ОДИН . 5 (5): e10892. Бибкод : 2010PLoSO...510892Z . дои : 10.1371/journal.pone.0010892 . ISSN 1932-6203 . ПМЦ 2878345 . ПМИД 20531940 .
- ^ Мейнхардт, Ганс (2008), «Модели формирования биологических паттернов: от элементарных шагов к организации эмбриональных осей», Многомасштабное моделирование систем развития , Актуальные темы биологии развития, том. 81, Elsevier, стр. 1–63, номер документа : 10.1016/s0070-2153(07)81001-5 , ISBN. 978-0-12-374253-7 , PMID 18023723
- ^ Хентшель, HGE; Глимм, Тильманн; Стекольщик, Джеймс А.; Ньюман, Стюарт А. (22 августа 2004 г.). «Динамические механизмы формирования скелетного рисунка конечностей позвоночных» . Труды Лондонского королевского общества. Серия Б: Биологические науки . 271 (1549): 1713–1722. дои : 10.1098/rspb.2004.2772 . ISSN 0962-8452 . ПМК 1691788 . ПМИД 15306292 .
- ^ Ландер, Артур Д. (январь 2007 г.). «Освобожденный Морфеус: переосмысление градиента морфогена» . Клетка . 128 (2): 245–256. дои : 10.1016/j.cell.2007.01.004 . ISSN 0092-8674 . ПМИД 17254964 . S2CID 14173945 .
- ^ Jump up to: а б Салазар-Сьюдад, Исаак; Джернвалл, Юкка (март 2010 г.). «Вычислительная модель зубов и причины морфологических изменений в развитии» . Природа . 464 (7288): 583–586. Бибкод : 2010Natur.464..583S . дои : 10.1038/nature08838 . ISSN 1476-4687 . ПМИД 20220757 . S2CID 323733 .
- ^ Салазар-Сьюдад, Исаак; Джернвалл, Юкка (январь 2004 г.). «Как различные типы механизмов формирования узоров влияют на эволюцию формы и развитие». Эволюция и развитие . 6 (1): 6–16. дои : 10.1111/j.1525-142x.2004.04002.x . ISSN 1520-541X . ПМИД 15108813 . S2CID 1783730 .
- ^ Риордон, Джеймс Р. (26 марта 2023 г.). «Сеянцы чиа подтверждают идеи Алана Тьюринга о закономерностях в природе» . Новости науки .
Дальнейшее чтение
[ редактировать ]- Болл, Филип (31 мая 2012 г.). «Шаблоны Тьюринга» . Химический мир . (См. также расширенную версию , июнь 2012 г.)
- Кампанья, Р.; Куомо, С.; Джаннино, Ф.; Северино, Г.; Торальдо, Дж. (6 декабря 2017 г.). «Полуавтоматический численный алгоритм формирования паттернов Тьюринга в модели реакции-диффузии» . Доступ IEEE . 6 : 4720–4724. дои : 10.1109/ACCESS.2017.2780324 .
- Ибер, Баньяр. «Шаблон Тьюринга» (PDF) . Вычислительная биология (CoBI) . Швейцария: ETH Цюрих . Проверено 16 августа 2018 г.
- Кейм, Брэндон (22 февраля 2011 г.). «Закономерности Алана Тьюринга в природе и за ее пределами» . Проводной .
- Уэллетт, Дженнифер (27 марта 2013 г.). «Когда математика встречается с природой: закономерности Тьюринга и константы формы» . Научный американец .
- Томпсон, Д'Арси Вентворт (1942) [1917]. О росте и форме . Издательство Кембриджского университета.