Сферический круг
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( Май 2024 г. ) |

В сферической геометрии сферический круг (часто сокращается до круга ) — это место геометрическое точек на сфере, находящихся на постоянном сферическом расстоянии ( сферический радиус ) от заданной точки на сфере (полюса или сферического центра ). Это кривая постоянной геодезической кривизны относительно сферы, аналогичная линии или кругу на евклидовой плоскости ; кривые, аналогичные прямым, называются большими кругами , а кривые, аналогичные плоским кругам, называются малыми кругами или меньшими кругами . Если сфера вложена в трехмерное евклидово пространство , ее окружности являются пересечениями сферы с плоскостями , а большие круги — пересечениями с плоскостями, проходящими через центр сферы.
Фундаментальные понятия
[ редактировать ]Внутренняя характеристика
[ редактировать ]Сферический круг с нулевой геодезической кривизной называется большим кругом и представляет собой геодезическую, аналогичную прямой линии на плоскости. Большой круг разделяет сферу на два равных полушария , границами каждого из которых является большой круг. Если большой круг проходит через точку на сфере, он также проходит через антиподальную точку (единственную самую дальнюю точку на сфере). Для любой пары различных неантиподальных точек через обе точки проходит единственный большой круг. Любые две точки большого круга разделяют его на две дуги, аналогичные отрезкам прямых на плоскости; более короткая называется малой дугой и представляет собой кратчайший путь между точками, а более длинная называется большой дугой .
Круг с ненулевой геодезической кривизной называется малым кругом и аналогичен кругу на плоскости. Маленький круг разделяет сферу на два сферических диска или сферических колпачка , граница каждого из которых — круг. Для любой тройки различных неантиподальных точек через все три проходит единственный маленький круг. Любые две точки маленького круга разделяют его на две дуги , аналогичные дугам окружности на плоскости.
Каждый круг имеет два противоположных полюса (или центра), присущих сфере. Большой круг равноудалён от своих полюсов, а малый круг ближе к одному полюсу, чем к другому. Концентрические круги иногда называют параллельными , потому что каждый из них находится на постоянном расстоянии друг от друга, и в частности от своего концентрического большого круга, и в этом смысле аналогичен параллельным линиям на плоскости.
Внешняя характеристика
[ редактировать ]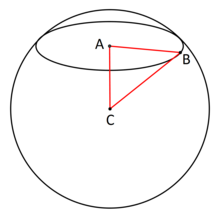
Если сфера изометрически встроена в евклидово пространство сферы , пересечение с плоскостью представляет собой круг, который внешне по отношению к сфере можно интерпретировать как евклидов круг: геометрическое место точек на плоскости на постоянном евклидовом расстоянии ( внешний радиус ). из точки плоскости ( внешний центр ). Большой круг лежит на плоскости, проходящей через центр сферы, поэтому его внешний радиус равен радиусу самой сферы, а его внешний центр является центром сферы. Маленький круг лежит на плоскости, не проходящей через центр сферы, поэтому его внешний радиус меньше, чем у сферы, а его внешний центр представляет собой произвольную точку внутри сферы. Параллельные плоскости разрезают сферу на параллельные (концентрические) маленькие круги; пара параллельных плоскостей, касающихся сферы, касаются полюсов этих окружностей, а диаметр через эти полюса, проходящий через центр сферы и перпендикулярный параллельным плоскостям, называется оси параллельных окружностей.
Пересечение сферы со второй сферой также является кругом, а пересечение сферы с концентрическим правым круговым цилиндром или правым круговым конусом представляет собой пару противоположных кругов.
Приложения
[ редактировать ]Геодезия
[ редактировать ]В географической системе координат на земном шаре параллели широты представляют собой маленькие круги, а экватор — единственный большой круг. Напротив, все меридианы долготы в паре с противоположным меридианом в другом полушарии образуют большие круги.
Ссылки
[ редактировать ]- Аллардис, Роберт Эдгар (1883), «Сферическая геометрия» , Труды Эдинбургского математического общества , 2 : 8–16, doi : 10.1017/S0013091500037020
- Кейси, Джон (1889), Трактат по сферической тригонометрии , Ходжес, Фиггис и др., ISBN 978-1-4181-8047-8
- Пападопулос, Атанас (2014), «О работах Эйлера и его последователей по сферической геометрии», Ганита Бхарати , 36 : 53–108, arXiv : 1409.4736
- Тодхантер, Исаак ; Литем, Джон Гастон (1901), Сферическая тригонометрия (пересмотренная редакция), Макмиллан
