Центральная линия (геометрия)

В геометрии , центральными линиями особые прямые линии лежащие в плоскости треугольника называются некоторые . Особое свойство, отличающее прямую как центральную, проявляется через уравнение прямой в трилинейных координатах . Это особое свойство также связано с концепцией центра треугольника . Понятие центральной линии было введено Кларком Кимберлингом в статье, опубликованной в 1994 году. ^[1]^[2]

Определение

Пусть $△ ABC$ — плоский треугольник и пусть $x : y : z$ — трилинейные координаты произвольной точки в плоскости треугольника $△ ABC$ .

Прямая в плоскости $△ ABC$ , уравнение которой в трилинейных координатах имеет вид $f(a,b,c)\,x+g(a,b,c)\,y+h(a,b,c)\,z=0$ где точка с трилинейными координатами $f(a,b,c):g(a,b,c):h(a,b,c)$ — центр треугольника, — центральная линия в плоскости $△ ABC$ относительно $△ ABC$ . ^[2]^[3]^[4]

Центральные линии как трилинейные поляры

Геометрическая связь между центральной линией и связанным с ней центром треугольника может быть выражена с использованием понятий трилинейных поляр и изогональных сопряжений .

Позволять $X=u(a,b,c):v(a,b,c):w(a,b,c)$ быть центром треугольника. Линия, уравнение которой ${\frac {x}{u(a,b,c)}}+{\frac {y}{v(a,b,c)}}+{\frac {z}{w(a,b,c)}}=0$ — трилинейная поляра треугольника $X.$ центра ^[2]^[5] Также точка $Y={\frac {1}{u(a,b,c)}}:{\frac {1}{v(a,b,c)}}:{\frac {1}{w(a,b,c)}}$ является изогонально-сопряженным центром треугольника $X$ .

Таким образом, центральная линия, заданная уравнением $f(a,b,c)\,x+g(a,b,c)\,y+h(a,b,c)\,z=0$ - трилинейная поляра изогонально-сопряженного центра треугольника $f(a,b,c):g(a,b,c):h(a,b,c).$

Строительство центральных линий

Пусть $X$ — любой центр треугольника $△ ABC$ .

Нарисуйте линии $AX, BX, CX$ и их отражения во внутренних биссектрисах углов при вершинах $A, B, C$ соответственно.
Отраженные линии совпадают, а точка совпадения является изогональной сопряженной $Y$ к $X$ .
Пусть чевианы $AY, BY, CY$ пересекают противоположные стороны $△ ABC$ в точках $A', B', C'$ соответственно. Треугольник $△ A'B'C'$ является чевианским треугольником $Y$ .
△ $DEF ABC$ и чевианский треугольник $△ A'B'C'$ находятся в перспективе, и пусть $будет$ осью перспективы двух треугольников. Линия $DEF$ точки $Y.$ является трилинейной полярой $DEF$ связанная с центром треугольника $X.$ — центральная линия ,

Некоторые названные центральные линии

Пусть $X n$ будет $n-м$ центром треугольника в Кларка Кимберлинга Энциклопедии центров треугольников . Центральная линия, связанная с $X n,$ обозначается $L n$ . Некоторые из названных центральных линий приведены ниже.

Центральная линия, связанная с X ₁ , центр: антиортическая ось.

Центральная линия, связанная с центром $X 1 = 1 : 1 : 1$ (также обозначаемая $I$ ), равна $x+y+z=0.$ Эта линия является антиортической осью $△ ABC$ . ^[6]

Изогональное сопряжение центра △ является $ABC самим$ центром. Таким образом, антиортическая ось, которая является центральной линией, связанной с инцентром, является осью перспективы $△ ABC$ и ее центральным треугольником (чевианский треугольник инцентра $△ ABC$ ).
Антиортическая ось $△ ABC$ осью перспективы △ $I ABC$ и эксцентральным треугольником $△ △ 1 I 2 I 3$ из $является ABC$ . ^[7]
Треугольник, боковые линии которого касаются внешними окружностями ABC $△,$ является треугольником, отходящим от $△ ABC$ . $△ ABC$ и прилегающий к нему треугольник находятся в перспективе, а ось перспективы является антиортической осью $△ ABC$ .

Центральная линия, связанная с X ₂ , центр тяжести: ось Лемуана.

Трилинейные координаты центроида X $2 ($ также обозначаемого $G$ ) $△ ABC$ : ${\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}$ Таким образом, центральная линия, связанная с центроидом, — это линия, трилинейное уравнение которой имеет вид ${\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}=0.$ Эта линия является осью Лемуана , также называемой линией Лемуана , линии $△ ABC$ .

Изогонально-сопряженным центроиду $X 2$ является точка симмедианы $X 6$ (также обозначаемая $K$ ), имеющая трилинейные координаты $a : b : c$ . Таким образом, ось Лемуана $△ ABC$ является трилинейной полярной точкой симмедианы $△ ABC$ .
Касательный треугольник к $△ ABC$ — это треугольник $△ T A T B T C,$ образованный касательными к описанной окружности $△ ABC$ в ее вершинах. $△ ABC$ и касательный к нему треугольник находятся в перспективе, а ось перспективы — это ось Лемуана $△ ABC$ .

Центральная линия, связанная с X ₃ , центром описанной окружности: ортическая ось.

Трилинейные координаты центра описанной окружности $X 3$ (также обозначаемого $O$ ) $△ ABC$ : $\cos A:\cos B:\cos C$ Таким образом, центральная линия, связанная с центром описанной окружности, — это линия, трилинейное уравнение которой имеет вид $x\cos A+y\cos B+z\cos C=0.$ является ортической осью △ $. ABC$ Эта линия ^[8]

Изогонально сопряженным центру описанной окружности $X 3$ является ортоцентр $X 4$ (также обозначаемый $H$ ), имеющий трилинейные координаты $sec A : sec B : sec C$ . Таким образом, ортическая ось $△ ABC$ является трилинейной полярной ортоцентром $△ ABC$ . Ортическая ось $△ ABC$ является осью перспективы $△ ABC$ и его ортического треугольника $△ H A H B H C$ . Это также радикальная ось описанной окружности треугольника и окружности из девяти точек.

Центральная линия, связанная с X ₄ , ортоцентром

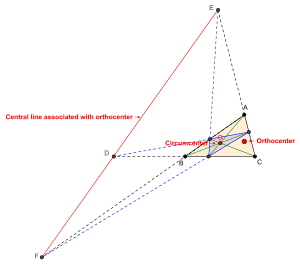
Трилинейные координаты ортоцентра X $4 ($ также обозначаемого $H$ ) $△ ABC$ : $\sec A:\sec B:\sec C$ Таким образом, центральная линия, связанная с центром описанной окружности, — это линия, трилинейное уравнение которой имеет вид $x\sec A+y\sec B+z\sec C=0.$

Изогонально сопряженный ортоцентру треугольника является центром описанной окружности треугольника. Таким образом, центральная линия, связанная с ортоцентром, является трилинейной полярой описанного центра.

Центральная линия, связанная с X ₅ , девятиточечным центром.

Трилинейные координаты девятиточечного центра $X 5$ (также обозначаемого $N$ ) $△ ABC$ : ^[9] $\cos(B-C):\cos(C-A):\cos(A-B).$ Таким образом, центральная линия, связанная с центром девяти точек, — это линия, трилинейное уравнение которой имеет вид $x\cos(B-C)+y\cos(C-A)+z\cos(A-B)=0.$

девятиточечному центру $△ ABC$ является точка Косницы $X 54$ △ $Изогонально- сопряженным ABC$ . ^[10]^[11] Таким образом, центральная линия, связанная с центром девяти точек, является трилинейной полярой точки Кошница.
Точка Кошницы строится следующим образом. Пусть $O$ — центр описанной окружности $△ ABC$ . Пусть $O A, OB, OC —$ центры описанных окружностей треугольников $△ BOC, △ COA, △ AOB$ соответственно. Прямые $AO A, BO B, CO C$ совпадают, а точка совпадения — это точка Кошницы $△ ABC$ . Название происходит от Дж. Ригби. ^[12]

Центральная линия, связанная с X ₆ , симмедианная точка: Бесконечная линия.

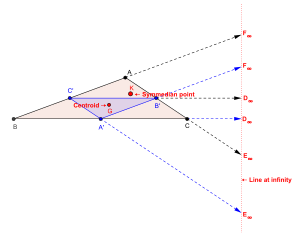
Трилинейные координаты симмедианной точки $X 6$ (также обозначаемой $K$ ) $△ ABC$ : $a:b:c$ Таким образом, центральная линия, связанная с симмедианной точкой, — это линия, трилинейное уравнение которой имеет вид $ax+by+cz=0.$

Эта линия является бесконечной линией в плоскости $△ ABC$ .
Изогонально сопряженная симедиана точки $△ ABC$ является центроидом $△ ABC$ . Следовательно, центральная линия, связанная с симмедианной точкой, является трилинейной полярой центроида. Это ось перспективы $△ ABC$ и ее медиального треугольника .

Еще несколько названных центральных линий

линия Эйлера

Линия Эйлера ABC $△ — это$ линия, проходящая через центр тяжести, центр описанной окружности, ортоцентр и девятиточечный центр $△ ABC$ . Трилинейное уравнение линии Эйлера имеет вид $x\sin 2A\sin(B-C)+y\sin 2B\sin(C-A)+z\sin 2C\sin(A-B)=0.$ Это центральная линия, связанная с центром треугольника $X 647$ .

Линия Нагеля

Линия Нагеля — это линия , $△ ABC$ проходящая через центроид, центр тяжести, центр Шпикера и Нагеля точку $△ ABC$ . Трилинейное уравнение линии Нагеля имеет вид $xa(b-c)+yb(c-a)+zc(a-b)=0.$ Это центральная линия, связанная с центром треугольника $X 649$ .

Ось Брокара

Ось Брокара ABC $△ — это линия ,$ проходящая через центр описанной окружности и симмедианную точку $△ ABC$ . Его трилинейное уравнение: $x\sin(B-C)+y\sin(C-A)+z\sin(A-B)=0.$ Это центральная линия, связанная с центром треугольника $X 523$ .

См. также

Ссылки

^ Кимберлинг, Кларк (июнь 1994 г.). «Центральные точки и центральные линии в плоскости треугольника». Журнал «Математика» . 67 (3): 163–187. дои : 10.2307/2690608 .
^ Jump up to: ^а ^б ^с Кимберлинг, Кларк (1998). Центры треугольников и центральные треугольники . Виннипег, Канада: Utilitas Mathematica Publishing, Inc., с. 285.
^ Вайсштейн, Эрик В. «Центральная линия» . Из MathWorld — веб-ресурса Wolfram . Проверено 24 июня 2012 г.
^ Кимберлинг, Кларк. «Глоссарий: Энциклопедия центров треугольников» . Архивировано из оригинала 23 апреля 2012 года . Проверено 24 июня 2012 г.
^ Вайсштейн, Эрик В. «Трилинейный полярный» . Из MathWorld — веб-ресурса Wolfram . Проверено 28 июня 2012 г.
^ Вайсштейн, Эрик В. «Антиортная ось» . Из MathWorld — веб-ресурса Wolfram . Проверено 28 июня 2012 г.
^ Вайсштейн, Эрик В. «Антиортная ось» . Из MathWorld — веб-ресурса Wolfram . Проверено 26 июня 2012 г.
^ Вайсштейн, Эрик В. «Ортическая ось» . Из MathWorld — веб-ресурса Wolfram .
^ Вайсштейн, Эрик В. «Девятиточечный центр» . Из MathWorld — веб-ресурса Wolfram . Проверено 29 июня 2012 г.
^ Вайсштейн, Эрик В. «Косница-Пойнт» . Из MathWorld — веб-ресурса Wolfram . Проверено 29 июня 2012 г.
^ Дарий Гринберг (2003). «О точке Косница и треугольнике отражения» (PDF) . Форум Геометрикорум . 3 : 105–111 . Проверено 29 июня 2012 г.
^ Дж. Ригби (1997). «Краткие заметки о некоторых забытых геометрических теоремах». Ежеквартальный журнал по математике и информатике . 7 : 156–158.

[1] Кимберлинг, Кларк (июнь 1994 г.). «Центральные точки и центральные линии в плоскости треугольника». Журнал «Математика» . 67 (3): 163–187. дои : 10.2307/2690608 .

[TCCT-2] Jump up to: ^а ^б ^с Кимберлинг, Кларк (1998). Центры треугольников и центральные треугольники . Виннипег, Канада: Utilitas Mathematica Publishing, Inc., с. 285.

[Eric-3] Вайсштейн, Эрик В. «Центральная линия» . Из MathWorld — веб-ресурса Wolfram . Проверено 24 июня 2012 г.

[4] Кимберлинг, Кларк. «Глоссарий: Энциклопедия центров треугольников» . Архивировано из оригинала 23 апреля 2012 года . Проверено 24 июня 2012 г.

[5] Вайсштейн, Эрик В. «Трилинейный полярный» . Из MathWorld — веб-ресурса Wolfram . Проверено 28 июня 2012 г.

[6] Вайсштейн, Эрик В. «Антиортная ось» . Из MathWorld — веб-ресурса Wolfram . Проверено 28 июня 2012 г.

[Eric2-7] Вайсштейн, Эрик В. «Антиортная ось» . Из MathWorld — веб-ресурса Wolfram . Проверено 26 июня 2012 г.

[8] Вайсштейн, Эрик В. «Ортическая ось» . Из MathWorld — веб-ресурса Wolfram .

[9] Вайсштейн, Эрик В. «Девятиточечный центр» . Из MathWorld — веб-ресурса Wolfram . Проверено 29 июня 2012 г.

[10] Вайсштейн, Эрик В. «Косница-Пойнт» . Из MathWorld — веб-ресурса Wolfram . Проверено 29 июня 2012 г.

[Darij-11] Дарий Гринберг (2003). «О точке Косница и треугольнике отражения» (PDF) . Форум Геометрикорум . 3 : 105–111 . Проверено 29 июня 2012 г.

[12] Дж. Ригби (1997). «Краткие заметки о некоторых забытых геометрических теоремах». Ежеквартальный журнал по математике и информатике . 7 : 156–158.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]