Симметрия отражения
Эта статья нуждается в дополнительных цитатах для проверки . ( октябрь 2015 г. ) |

В математике , симметрия отражения — симметрия линий , зеркальная симметрия или симметрия зеркального изображения это симметрия относительно отражения . То есть фигура, которая не изменяется при отражении, обладает отражательной симметрией.
В 2D есть линия/ось симметрии, в 3D симметрии — плоскость . называется предмет или фигура, неотличимые от своего преобразованного изображения Зеркально-симметричным . В заключение отметим, что линия симметрии делит фигуру пополам, и эти половины должны быть идентичными.
Симметричная функция
[ редактировать ]
Формально математический объект является симметричным относительно заданной операции, такой как отражение, вращение или перемещение , если при применении к объекту эта операция сохраняет какое-то свойство объекта. [1] Совокупность операций, сохраняющих данное свойство объекта, образует группу . Два объекта симметричны друг другу относительно заданной группы операций, если один получается из другого посредством некоторых операций (и наоборот).
Симметричная функция двумерной фигуры — это такая линия, что для каждого построенного перпендикуляра , если перпендикуляр пересекает фигуру на расстоянии d от оси вдоль перпендикуляра, то существует еще одно пересечение формы и перпендикуляра. , на том же расстоянии d от оси, в противоположном направлении вдоль перпендикуляра.
Другой способ представить симметричную функцию состоит в том, что если фигуру сложить пополам по оси, две половины будут идентичны: две половины являются зеркальными отражениями друг друга . [1]
Таким образом, квадрат имеет четыре оси симметрии, потому что есть четыре разных способа сложить его, чтобы все края совпадали. У окружности бесконечно много осей симметрии.
Симметричные геометрические фигуры
[ редактировать ]
|
|
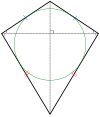
| равнобедренная трапеция и воздушный змей | |
|---|---|

|
|
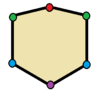
| Шестиугольники | |
|
|
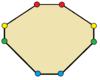
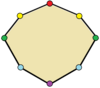
| восьмиугольники | |
Треугольники с зеркальной симметрией являются равнобедренными . Четырехугольники с зеркальной симметрией — это воздушные змеи , (вогнутые) дельтоиды, ромбы , [2] и равнобедренные трапеции . Все многоугольники с четными сторонами имеют две простые отражающие формы: одну с линиями отражения через вершины, а другую через края.
Для произвольной формы аксиальность формы измеряет, насколько она близка к двусторонней симметрии. Он равен 1 для форм с отражательной симметрией и от 2/3 до 1 для любой выпуклой формы.
Расширенные типы симметрии отражения
[ редактировать ]Для более общих типов отражения соответственно существуют более общие типы отражательной симметрии. Например:
- относительно неизометрической аффинной инволюции ( наклонного отражения в прямой, плоскости и т.п.)
- относительно инверсии круга .
На природе
[ редактировать ]
Животные с двусторонней симметрией обладают зеркальной симметрией вокруг сагиттальной плоскости, которая делит тело по вертикали на левую и правую половины, по одному органу чувств и паре конечностей с каждой стороны. Большинство животных двусторонне симметричны, вероятно, потому, что это способствует движению вперед и обтекаемости . [3] [4] [5] [6]
В архитектуре
[ редактировать ]
Зеркальная симметрия часто используется в архитектуре например, фасад Санта-Мария-Новелла , как , во Флоренции . [7] Он также встречается в дизайне древних сооружений, таких как Стоунхендж . [8] Симметрия была основным элементом в некоторых стилях архитектуры, таких как палладианство . [9]
См. также
[ редактировать ]- Узоры в природе
- точечного отражения Симметрия
- Теория групп Кокстера о группах отражений в евклидовом пространстве
- Вращательная симметрия (различный тип симметрии)
- Хиральность
Ссылки
[ редактировать ]- ^ Jump up to: а б Стюарт, Ян (2001). Какой формы снежинка? Магические числа в природе . Вайденфельд и Николсон. п. 32.
- ^ Галлберг, Ян (1997). Математика: от рождения чисел . WW Нортон. стр. 394–395 . ISBN 0-393-04002-Х .
- ^ Валентайн, Джеймс В. «Билатерия» . ДоступНаука . Проверено 29 мая 2013 г.
- ^ «Двусторонняя симметрия» . Музей естественной истории . Проверено 14 июня 2014 г.
- ^ Финнерти, Джон Р. (2005). «Способствовал ли внутренний транспорт, а не направленное передвижение, развитию двусторонней симметрии у животных?» (PDF) . Биоэссе . 27 (11): 1174–1180. дои : 10.1002/bies.20299 . ПМИД 16237677 .
- ^ «Двусторонняя (левая/правая) симметрия» . Беркли . Проверено 14 июня 2014 г.
- ^ Тавернор, Роберт (1998). Об Альберти и строительном искусстве . Издательство Йельского университета. стр. 102–106. ISBN 978-0-300-07615-8 .
Более точные исследования показывают, что фасаду не хватает точной симметрии, но не может быть никаких сомнений в том, что Альберти хотел, чтобы композиция числа и геометрии считалась идеальной. Фасад умещается на площади в 60 флорентийских локтей.
- ^ Джонсон, Энтони (2008). Разгадка Стоунхенджа: новый ключ к древней загадке . Темза и Гудзон.
- ^ Уотерс, Сюзанна. «Палладианство» . Королевский институт британских архитекторов . Проверено 29 октября 2015 г.
Библиография
[ редактировать ]Общий
[ редактировать ]- Стюарт, Ян (2001). Какой формы снежинка? Магические числа в природе . Вайденфельд и Николсон.
Передовой
[ редактировать ]- Вейль, Герман (1982) [1952]. Симметрия . Принстон: Издательство Принстонского университета. ISBN 0-691-02374-3 .