Полиномы Макдональда

В математике полиномы Макдональда P _λ ( x ; t , q ) представляют собой семейство ортогональных симметричных полиномов от нескольких переменных, введенных Макдональдом в 1987 году. Позже он представил несимметричное обобщение в 1995 году. Макдональд первоначально связал свои полиномы с весами λ. конечных систем корней и использовал только одну переменную t , но позже понял, что более естественно связать их с аффинными системами корней, а не с конечными системами корней, и в этом случае переменную t можно заменить несколькими разными переменными t =( t ₁ ,..., t _k ), по одному на каждую из k орбит корней аффинной системы корней. Полиномы Макдональда — это полиномы от n переменных x = ( x ₁ ,..., x _n ), где n — ранг аффинной корневой системы. Они обобщают многие другие семейства ортогональных полиномов, такие как полиномы Джека и полиномы Холла-Литтлвуда и полиномы Аски-Уилсона , которые, в свою очередь, включают большинство названных ортогональных полиномов с 1 переменной как частные случаи. Полиномы Курнвиндера представляют собой полиномы Макдональда некоторых нередуцированных корневых систем. У них глубокие отношения с аффинные алгебры Гекке и схемы Гильберта , которые были использованы для доказательства нескольких гипотез, сделанных о них Макдональдом.

Определение

Сначала исправьте некоторые обозначения:

• R конечная система корней в вещественном векторном пространстве V. —
• Р ⁺ есть выбор положительных корней , которым соответствует положительная камера Вейля .
• W — Вейля R. ​ группа
• Q — решетка корней R (решетка, натянутая на корни).
• P — весов решетка R (содержащая Q ).
• Порядок по весам : $\mu \leq \lambda$ тогда и только тогда, когда $\lambda -\mu$ является неотрицательной линейной комбинацией простых корней .
• П ⁺ представляет собой набор доминирующих весов: элементы P в положительной камере Вейля.
• ρ — вектор Вейля : половина суммы положительных корней; это особый элемент P ⁺ внутри положительной камеры Вейля.
• F — поле характеристики 0, обычно это рациональные числа.
• A = F ( P ) — групповая алгебра P записанным с базисом элементов, e ^л ∈ P. для λ
• Если f = е ^л , тогда f означает e ^-л , и это распространяется по линейности на всю групповую алгебру.
• m _µ = Σ _{λ ∈ W µ} e ^л – орбитальная сумма; эти элементы составляют основу подалгебры A ^В элементов, фиксированных W .
• $(a;q)_{\infty }=\prod _{r\geq 0}(1-aq^{r})$, бесконечный символ q-Похгаммера .
• $\Delta =\prod _{\alpha \in R}{(e^{\alpha };q)_{\infty } \over (te^{\alpha };q)_{\infty }}.$
• $\langle f,g\rangle =({\text{constant term of }}f{\overline {g}}\Delta )/|W|$ является скалярным произведением двух элементов A , по крайней мере, когда t является положительной целой степенью q .

Полиномы Макдональда P _λ для λ ∈ P ⁺ однозначно определяются следующими двумя условиями:

$P_{\lambda }=\sum _{\mu \leq \lambda }u_{\lambda \mu }m_{\mu }$ где u _λμ — рациональная функция от q и t , причем u _λλ = 1;

P _λ и P _µ ортогональны, если λ < µ.

Другими словами, полиномы Макдональда получаются путем ортогонализации очевидного базиса для A ^В . Существование полиномов с такими свойствами легко показать (для любого скалярного произведения). Ключевым свойством полиномов Макдональда является то, что они ортогональны : 〈 P _λ , P _µ 〉 = 0 всякий раз, когда λ ≠ µ. Это нетривиальное следствие определения, поскольку P ⁺ не является полностью упорядоченным и поэтому содержит множество несравнимых элементов. Таким образом, необходимо проверить, что соответствующие многочлены по-прежнему ортогональны. Ортогональность можно доказать, показав, что полиномы Макдональда являются собственными векторами. для алгебры коммутирующих самосопряженных операторов с одномерными собственными пространствами и используя тот факт, что собственные пространства для разных собственных значений должны быть ортогональными.

В случае непростых корневых систем (B, C, F, G) параметр t можно выбрать изменяющимся в зависимости от длины корня, что дает трехпараметрическое семейство полиномов Макдональда. Можно также распространить определение на нередуцированную корневую систему BC, и в этом случае получится семейство с шестью параметрами (один t для каждой орбиты корней плюс q ), известное как полиномы Курнвиндера . Иногда лучше рассматривать полиномы Макдональда как зависящие от возможно нередуцированной аффинной корневой системы. В этом случае существует один параметр t, связанный с каждой орбитой корней в аффинной корневой системе, плюс один параметр q . Число витков корней может варьироваться от 1 до 5.

Примеры

• Если q = t, то полиномы Макдональда становятся характерами Вейля представлений компактной группы корневой системы или функциями Шура в случае корневых систем A. типа
• Если q = 0, полиномы Макдональда становятся (перемасштабированными) зональными сферическими функциями для полупростой p -адической группы или полиномами Холла – Литтлвуда , когда корневая система имеет тип A .
• Если t = 1, полиномы Макдональда становятся суммами по W орбитам, которые являются мономиальными симметричными функциями, когда корневая система имеет тип A .
• Если положить t = q ^а и пусть q стремится к 1, полиномы Макдональда становятся полиномами Джека, когда корневая система имеет тип A , и полиномами Хекмана – Опдама для более общих корневых систем.
• Для аффинной корневой системы A1 _{полиномами} полиномы Макдональда являются Роджерса .
• Для нередуцированной аффинной корневой системы ранга 1 типа ( C ^∨
  ₁ , C ₁ ), полиномы Макдональда представляют собой полиномы Аски–Вильсона , которые, в свою очередь, включают в себя в качестве частных случаев большинство названных семейств ортогональных полиномов от 1 переменной.
• Для нередуцированной аффинной корневой системы типа ( C ^∨
  _n , C _n ), полиномы Макдональда являются полиномами Курнвиндера .

Гипотеза постоянного члена Макдональда

Если т = q ^к для некоторого положительного целого числа k норма полиномов Макдональда определяется выражением

$\langle P_{\lambda },P_{\lambda }\rangle =\prod _{\alpha \in R,\alpha >0}\prod _{0<i<k}{1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))+i} \over 1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))-i}}.$

Это было высказано Макдональдом (1982) как обобщение гипотезы Дайсона и доказано для всех (приведенных) корневых систем Чередником (1995) с использованием свойств дважды аффинных алгебр Гекке . Гипотеза ранее была доказана в каждом конкретном случае типа En _{для всех систем корней, кроме систем} несколькими авторами .

Есть две другие гипотезы, которые вместе с гипотезой о норме в этом контексте называются гипотезами Макдональда: в дополнение к формуле для нормы Макдональд выдвинул гипотезу о формуле для значения P _λ в точке t ^р и симметрия

${\frac {P_{\lambda }(\dots ,q^{\mu _{i}}t^{\rho _{i}},\dots )}{P_{\lambda }(t^{\rho })}}={\frac {P_{\mu }(\dots ,q^{\lambda _{i}}t^{\rho _{i}},\dots )}{P_{\mu }(t^{\rho })}}.$

Опять же, они были доказаны для общих приведенных корневых систем Чередником ( 1995 ) с использованием двойных аффинных алгебр Гекке с вскоре после этого расширением на случай BC благодаря работам ван Диена, Ноуми и Сахи.

Гипотеза Макдональда о позитивности

В случае систем корней типа A _{n −1} полиномы Макдональдаявляются просто симметричными полиномами от n переменных с коэффициентами, которые являются рациональными функциями q и t . Определенная трансформированная версия ${\widetilde {H}}_{\mu }$ полиномов Макдональда (см. Комбинаторную формулу ниже) образуют ортогональный базис пространства симметричных функций над $\mathbb {Q} (q,t)$, и поэтому может быть выражено через функции Шура $s_{\lambda }$. Коэффициенты K _λμ ( q , t ) этих соотношений называются коэффициентами Костки–Макдональда или qt -коэффициентами Костки.Макдональд предположил, что коэффициенты Костки – Макдональда представляют собой полиномы от q и t с неотрицательными целыми коэффициентами. Эти предположения теперь доказаны; самым трудным и последним шагом было доказательство положительности, которое было сделано Марком Хейманом (2001), доказав n ! предположение .

-Костки по-прежнему остается центральной открытой проблемой алгебраической комбинаторики Нахождение комбинаторной формулы для коэффициентов qt .

н! догадка

Затем ​ ! Гипотеза Адриано Гарсиа и Марка Хаймана утверждает, что для каждого разбиения µ числа n пространство

$D_{\mu }=C[\partial _{x},\partial _{y}]\,\Delta _{\mu }$

натянутый на все высшие частные производные

$\Delta _{\mu }=\det(x_{i}^{p_{j}}y_{i}^{q_{j}})_{1\leq i,j,\leq n}$

имеет размерность n !, где ( p _j , q _j ) пробегают n элементов диаграммы разбиения µ, рассматриваемого как подмножество пар неотрицательных целых чисел. Например, если µ — это разбиение 3 = 2 + 1 числа n = 3, то пары ( p _j , q _j ) являются(0, 0), (0, 1), (1, 0), а пространство D _µ натянуто на

$\Delta _{\mu }=x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}$

$y_{2}-y_{3}$

$y_{3}-y_{1}$

$x_{3}-x_{2}$

$x_{1}-x_{3}$

$1$

который имеет размерность 6 = 3!.

Доказательство Хаймана гипотезы Макдональда о положительности и n ! Гипотеза заключалась в том, чтобы показать, что изоспектральная схема Гильберта из n точек на плоскости была схемой Коэна – Маколея (и даже Горенштейна ). Более ранние результаты Хаймана и Гарсиа уже показали, что это подразумевает n ! гипотеза, и что n ! Гипотеза подразумевала, что коэффициенты Костки–Макдональда представляют собой градуированные кратности характеров для модулей D _µ . Это немедленно подразумевает гипотезу Макдональда о положительности, поскольку кратность символов должна быть неотрицательными целыми числами.

Ян Гройновски и Марк Хейман нашли еще одно доказательство гипотезы Макдональда о положительности, доказав гипотезу о положительности для полиномов LLT .

Комбинаторная формула для полиномов Макдональда

В 2005 г. Дж. Хаглунд, М. Хайман и Н. Лоер. дал первое доказательство комбинаторной интерпретации Полиномы Макдональда. В 1988 году И.Г. Макдональд дал второе доказательство комбинаторной интерпретации полиномов Макдональда (уравнения (4.11) и (5.13)).Формула Макдональда отличается от формулы Хаглунда, Хаймана и Лоэра и содержит гораздо меньше членов (эта формула доказана также в основополагающей работе Макдональда Ч. VI (7.13)). Хотя их комбинаторные формулы очень полезны для вычислений и интересны сами по себе, они не сразу подразумевают положительность коэффициентов Костки-Макдональда. $K_{\lambda \mu }(q,t),$ поскольку они дают разложение полиномов Макдональда в мономиальные симметричные функции, а не в функции Шура.

Записано в преобразованных полиномах Макдональда. ${\widetilde {H}}_{\mu }$ а не обычный $P_{\lambda }$, они есть

${\widetilde {H}}_{\mu }(x;q,t)=\sum _{\sigma :\mu \to \mathbb {Z} _{+}}q^{inv(\sigma )}t^{maj(\sigma )}x^{\sigma }$

где σ — заполнение диаграммы Юнга формы µ, inv и maj — некоторые комбинаторные статистики (функции), определенные на заполнении σ. Эта формула выражает полиномы Макдональда от бесконечного числа переменных. Чтобы получить полиномы от n переменных, просто ограничьте формулу заполнениями, в которых используются только целые числа 1, 2, ..., n . Термин х ^п следует интерпретировать как $x_{1}^{\sigma _{1}}x_{2}^{\sigma _{2}}\cdots$ где σi _— количество ячеек в заполнении µ содержимым i .

Это изображает руку и ногу квадрата диаграммы Юнга. Рука — это количество клеток справа от нее, а нога — количество клеток над ней.

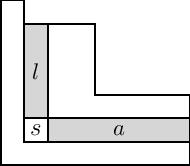
Преобразованные полиномы Макдональда ${\widetilde {H}}_{\mu }(x;q,t)$ в приведенной выше формуле связаны с классическими полиномами Макдональда $P_{\lambda }$ через последовательность преобразований. Во-первых, интегральная форма полиномов Макдональда, обозначаемая $J_{\lambda }(x;q,t)$, представляет собой повторное масштабирование $P_{\lambda }(x;q,t)$ что очищает знаменатели коэффициентов:

$J_{\lambda }(x;q,t)=\prod _{s\in D(\lambda )}(1-q^{a(s)}t^{1+l(s)})\cdot P_{\lambda }(x;q,t)$

где $D(\lambda )$ представляет собой совокупность квадратов диаграммы Юнга $\lambda$, и $a(s)$ и $l(s)$ обозначаем руку и ногу квадрата $s$, как показано на рисунке. Примечание. На рисунке справа используется французская нотация таблицы, которая перевернута вертикально по сравнению с английской нотацией, используемой на странице Википедии для диаграмм Янга. Французские обозначения чаще используются при изучении полиномов Макдональда.

Преобразованные полиномы Макдональда ${\widetilde {H}}_{\mu }(x;q,t)$ тогда можно определить с точки зрения $J_{\mu }$х. У нас есть

${\widetilde {H}}_{\mu }(x;q,t)=t^{-n(\mu )}J_{\mu }\left[{\frac {X}{1-t^{-1}}};q,t^{-1}\right]$

где

$n(\mu )=\sum _{i}\mu _{i}\cdot (i-1).$

Обозначение скобок выше обозначает плетистическую замену .

Эту формулу можно использовать для доказательства формулы Кнопа и Сахи для полиномов Джека .

Несимметричные полиномы Макдональда

В 1995 году Макдональд представил несимметричный аналог симметричных полиномов Макдональда:а симметричные полиномы Макдональда можно легко восстановить из несимметричного аналога.В своем первоначальном определении он показывает, что несимметричные полиномы Макдональда представляют собой уникальное семейство полиномов. многочлены, ортогональные определенному скалярному произведению, а также удовлетворяющие Свойство треугольности при разложении по мономиальному базису.

В 2007 году Хаглунд, Хайман и Лоер дали комбинаторную формулу для несимметричных полиномов Макдональда.

Несимметричные полиномы Макдональда специализируются на символах Демазюра, принимая q=t=0,и ключевым полиномам, когда q=t=∞.

Комбинаторные формулы, основанные на процессе исключения

В 2018 году С. Кортил , О. Мандельштам и Л. Уильямс использовали процесс исключения, чтобы дать прямую комбинаторную характеристику как симметричных, так и несимметричных полиномов Макдональда. Их результаты отличаются от более ранних работ Хаглунда отчасти потому, что они дают формулу непосредственно для полиномов Макдональда, а не ее преобразование. Они развивают концепцию многострочной очереди, которая представляет собой матрицу, содержащую шары или пустые ячейки вместе с сопоставлением шаров и их соседей и комбинаторным механизмом маркировки. Тогда несимметричный полином Макдональда удовлетворяет:

$E_{\lambda }({\textbf {x}};q,t)=\sum _{Q}\mathrm {wt} (Q)$

где сумма равна всем $L\times n$ многострочные очереди типа $\lambda$ и $\mathrm {wt}$ — это весовая функция, сопоставляющая эти очереди с конкретными полиномами. Симметричный полином Макдональда удовлетворяет:

$P_{\lambda }({\textbf {x}};q,t)=\sum _{\mu }E_{\mu }(x_{1},...,x_{n};q,t)=\sum _{\mu }\sum _{Q}\mathrm {wt} (Q)$

где внешняя сумма рассчитывается по всем различным композициям $\mu$ которые представляют собой перестановки $\lambda$, а внутренняя сумма такая же, как и раньше.

Библиография

• Чередник, Иван (1995), «Двойные аффинные алгебры Гекке и гипотезы Макдональда», Annals of Mathematics , Вторая серия, 141 (1), Annals of Mathematics: 191–216, doi : 10.2307/2118632 , ISSN   0003-486X , JSTOR   2118632
• Гарсия, Адриано; Реммель, Джеффри Б. (15 марта 2005 г.), « Прорывы в теории полиномов Макдональда », PNAS , 102 (11): 3891–3894, Bibcode : 2005PNAS..102.3891G , doi : 10.1073/pnas.0409705102 , PMC   554818 , PMID   15753285
• Марк Хейман Комбинаторика, симметричные функции и схемы Гильберта. Современные достижения в математике. 2002, вып. 1 (2002), 39–111.
• Хайман, Марк Заметки о полиномах Макдональда и геометрии схем Гильберта. Симметричные функции 2001: обзоры событий и перспектив, 1–64, NATO Sci. Сер. II Матем. Физ. хим., 74 года, Клюверская академия. Изд., Дордрехт, 2002. МР. 2059359
• Хайман, Марк (2001), « Схемы Гильберта, полиграфы и гипотеза положительности Макдональда », J. Amer. Математика. Соц. , 14 (4): 941–1006, arXiv : math.AG/0010246 , doi : 10.1090/S0894-0347-01-00373-3 , S2CID   9253880
• Кириллов А.А. (1997), "Лекции по аффинным алгебрам Гекке и гипотезам Макдональда" , Бюлл. амер. Математика. Соц. , 34 (3): 251–292, doi : 10.1090/S0273-0979-97-00727-1
• Макдональд, И.Г. (1982), «Некоторые гипотезы о корневых системах», SIAM Journal on Mathematical Analysis , 13 (6): 988–1007, doi : 10.1137/0513070 , ISSN   0036-1410 , MR   0674768
• Макдональд, И.Г. Симметричные функции и полиномы Холла. Второе издание. Оксфордские математические монографии. Оксфордские научные публикации. The Clarendon Press, Oxford University Press, Нью-Йорк, 1995. x+475 стр. ISBN   0-19-853489-2 МР 1354144
• Макдональд, И.Г. Симметричные функции и ортогональные многочлены. Мемориальные лекции декана Жаклин Б. Льюис, прочитанные в Университете Рутгерса, Нью-Брансуик, Нью-Джерси. Серия университетских лекций, 12. Американское математическое общество, Провиденс, Род-Айленд, 1998. xvi+53 стр. ISBN   0-8218-0770-6 МР 1488699
• Макдональд, И.Г. Аффинные алгебры Гекке и ортогональные многочлены. Семинар Бурбаки 797 (1995).
• Макдональд, И.Г. (2000–2001), «Ортогональные полиномы, связанные с корневыми системами», Séminaire Lotharingien de Combinatoire , 45 : Art. B45a, arXiv : math.QA/0011046 , MR   1817334
• Макдональд, И.Г. (2003), Аффинные алгебры Гекке и ортогональные полиномы , Кембриджские трактаты по математике, том. 157, Кембридж: Издательство Кембриджского университета, стр. x+175, ISBN  978-0-521-82472-9 , г-н   : 1976581

Внешние ссылки

• Страница Майка Заброцкого о полиномах Макдональда .
• Некоторые статьи Хеймана о полиномах Макдональда.