Джованни Баттиста Риччоли

«Риччоли» перенаправляется сюда. Чтобы узнать о других значениях, см. Риччоли (значения) .

преподобный Джованни Баттиста Риччоли
Рожденный	Галеаццо Риччоли ( 1598-04-17 ) 17 апреля 1598 г. Феррара , Папская область
Умер	25 июня 1671 г. ( 1671-06-25 ) (73 года) Болонья , Папская область
Национальность	итальянский
Известный	Опыты с маятниками и падающими телами. Знакомство с действующей схемой лунной номенклатуры
Родители)	Джованни Баттиста Риччоли и Гаспара Риччоли (урожденная Орсини)
Научная карьера
Поля	Астрономия , экспериментальная физика , география , хронология

Джованни Баттиста Риччоли , SJ (17 апреля 1598 — 25 июня 1671) — итальянский астроном и католический священник ордена иезуитов . Он известен, среди прочего, своими экспериментами с маятниками и падающими телами, обсуждением 126 аргументов, касающихся движения Земли, а также введением нынешней схемы лунной номенклатуры . Он также широко известен открытием первой двойной звезды. Он утверждал, что вращение Земли должно проявляться, потому что на вращающейся Земле земля в разное время движется с разной скоростью.

Биография

Риччоли, изображенный в Атласе Целестис 1742 года (иллюстрация 3) Иоганна Габриэля Доппельмайера.

Риччоли родился в Ферраре . Он вступил в Общество Иисуса 6 октября 1614 года. После завершения послушничества он начал изучать гуманитарные науки в 1616 году, продолжая эти исследования сначала в Ферраре, а затем в Пьяченце .

колледже С 1620 по 1628 год изучал философию и теологию в Пармском . Пармские иезуиты разработали мощную программу экспериментов, например, с падающими телами. Один из самых известных итальянских иезуитов того времени, Джузеппе Бьянкани (1565–1624), преподавал в Парме, когда туда прибыл Риччоли. Бьянкани принял новые астрономические идеи, такие как существование лунных гор и текучая природа небес, и сотрудничал с астрономом-иезуитом Кристофом Шайнером (1573–1650) в наблюдениях солнечных пятен. Риччоли упоминает его с благодарностью и восхищением.

К 1628 году обучение Риччоли было завершено, и он был рукоположен . Он просил миссионерскую работу, но эта просьба была отклонена. Вместо этого ему поручили преподавать в Парме. Там он преподавал логику, физику и метафизику с 1629 по 1632 год, а также проводил эксперименты с падающими телами и маятниками. В 1632 году он стал членом группы, которой было поручено формирование молодых иезуитов, среди которых Даниэлло Бартоли . Он провел 1633–1634 учебный год в Мантуе , где сотрудничал с Никколо Кабео (1576–1650) в дальнейших исследованиях маятника. В 1635 году он вернулся в Парму, где преподавал богословие, а также провел свое первое важное наблюдение Луны. В 1636 году его отправили в Болонью в качестве профессора богословия.

Риччоли называл себя богословом, но с сильным и постоянным интересом к астрономии еще со студенческих лет, когда он учился у Бьянкани. Он сказал, что многие иезуиты были теологами, но немногие были астрономами. Он сказал, что, как только в нем возник энтузиазм к астрономии, он уже никогда не смог его погасить, и поэтому он стал более предан астрономии, чем теологии. В конце концов его начальство в ордене иезуитов официально поручил ему астрономические исследования. Однако он также продолжал писать по теологии (см. ниже ).

Риччоли построил в Болонье астрономическую обсерваторию при колледже Сент-Люсии, оснащенную множеством инструментов для астрономических наблюдений, включая телескопы , квадранты , секстанты и другие традиционные инструменты. Риччоли в своих исследованиях занимался не только астрономией, но и физикой, арифметикой, геометрией, оптикой, гномоникой , географией и хронологией. В своей работе он сотрудничал с другими, в том числе с другими иезуитами, в первую очередь с Франческо Марией Гримальди (1618–1663) в Болонье, и поддерживал обширную переписку с другими людьми, разделявшими его интересы, включая Гевелия , Гюйгенса , Кассини и Кирхера .

Он был награжден премией Людовика XIV в знак признания его деятельности и ее значения для современной культуры.

Риччоли продолжал публиковать публикации как по астрономии, так и по теологии до своей смерти. Он умер в Болонье в возрасте 73 лет.

Научная работа

Новый Завет

Фазы серпа Венеры и подробные изображения ее внешнего вида в телескоп из « Нового Альмагеста» Риччоли 1651 года .

Одной из самых значительных работ Риччоли был его Almagestum Novum ( «Новый Альмагест ») 1651 года. энциклопедический труд, состоящий из более чем 1500 страниц-листов (38 х 25 см), плотно заполненных текстом, таблицами и иллюстрациями. Он стал стандартным техническим справочником для астрономов всей Европы: Джон Флемстид (1646–1719), первый английский астроном королевской семьи, коперниканец и протестант, использовал его для своих лекций в Грешаме ; Жером Лаланд (1732–1807) из Парижской обсерватории широко цитировал его. хотя на тот момент это была старая книга; 1912 года Католическая энциклопедия называет это самым важным литературным произведением иезуитов семнадцатого века. В его двух томах было десять «книг», охватывающих все предметы астрономии, связанные с астрономией того времени:

1. небесная сфера и такие предметы, как небесные движения, экватор, эклиптика, зодиак и т. д.
2. Земля и ее размеры, гравитация и маятниковое движение и т. д.
3. Солнце, его размер и расстояние, его движение, наблюдения с его участием и т. д.
4. Луна, ее фазы, размер и расстояние и т. д. (прилагались подробные карты Луны, видимой в телескоп)
5. лунные и солнечные затмения
6. неподвижные звезды
7. планеты и их движения и т. д. (были включены изображения каждой из них, видимые в телескоп);
8. кометы и новые («новые звезды»)
9. строение Вселенной — гелиоцентрическая и геоцентрическая теории и т. д.
10. расчеты, связанные с астрономией.

Риччоли предполагал, что « Новый Альмагест» будет состоять из трех томов, но был завершен только первый (1500 страниц, разделенный на две части).

Маятники и падающие тела

Риччоли приписывают то, что он был первым человеком, точно измерившим ускорение силы тяжести падающих тел. Книги 2 и 9 « Нового Альмагеста Риччоли» включали подробное обсуждение и обширные экспериментальные отчеты о движении падающих тел и маятников.

Его интересовал маятник как прибор для точного измерения времени. Подсчитав количество качаний маятника, прошедших между прохождениями определенных звезд, Риччоли смог экспериментально убедиться, что период качания маятника с малой амплитудой постоянен с точностью до двух колебаний из 3212 (0,062%). Он также сообщил, что период маятника увеличивается, если амплитуда его качания увеличивается до 40 градусов. Он стремился разработать маятник, период которого составлял бы ровно одну секунду – такой маятник мог бы совершить 86 400 колебаний за 24 часа. Он дважды проверил это непосредственно, используя звезды для отметки времени и набрав команду из девяти коллег-иезуитов для подсчета колебаний и поддержания амплитуды колебаний в течение 24 часов. В результате получились маятники с периодами в пределах 1,85%, а затем 0,69% от желаемого значения; и Риччоли даже стремился улучшить последнее значение. Затем секундный маятник использовался в качестве эталона для калибровки маятников с разными периодами. Риччоли говорил, что маятник не является абсолютно надежным инструментом для измерения времени, но по сравнению с другими методами он является чрезвычайно надежным инструментом.

С помощью маятников, позволяющих отслеживать время (иногда дополненных хором иезуитов, поющих в такт, с маятником, обеспечивающим звуковой таймер) и высокой конструкцией в виде Болонской башни Азинелли, из которой можно было сбрасывать предметы, Риччоли мог точно эксперименты с падающими телами. Он подтвердил, что падающие тела подчиняются правилу «нечетных чисел» Галилея, так что расстояние, пройденное падающим телом, увеличивается пропорционально квадрату времени падения, что указывает на постоянное ускорение. По мнению Риччоли, падающее тело, вышедшее из состояния покоя, проходит 15 римских футов (4,44 м) за одну секунду, 60 футов (17,76 м) за две секунды, 135 футов (39,96 м) за три секунды и т. д. Другие иезуиты, такие как вышеупомянутый Кабео, утверждали, что это правило не было строго продемонстрировано. Его результаты показали, что, хотя падающие тела обычно демонстрировали постоянное ускорение, существовали различия, определяемые весом, размером и плотностью. Риччоли говорил, что если два тяжелых предмета разного веса бросить одновременно с одной и той же высоты, то более тяжелый из них опустится быстрее, если он имеет одинаковую или большую плотность; если оба объекта имеют одинаковый вес, более плотный опускается быстрее.

Например, роняя шарики из дерева и свинца, которые весили 2,5 унции, Риччоли обнаружил, что после того, как свинцовый шар прошел 280 римских футов, деревянный шар прошел только 240 футов (таблица в « Новом Альмагесте» содержит данные о двадцати одной такой паре). капли). Он объяснил такие различия воздухом и отметил, что при падении тел необходимо учитывать плотность воздуха. Он проиллюстрировал надежность своих экспериментов, предоставив подробные описания того, как они проводились, чтобы каждый мог их воспроизвести. в комплекте со схемами Торре де Азинелли с указанием высоты, мест падения и т. д.

Риччоли отмечал, что, хотя эти различия действительно противоречат утверждению Галилея о том, что шары разного веса будут падать с одинаковой скоростью, возможно, Галилей наблюдал падение тел, сделанных из одного и того же материала, но разных размеров, поскольку в этом случае разница во времени падения между двумя шарами намного меньше, чем если бы шары были одного размера, но из разных материалов, или одного и того же веса, но разных размеров и т. д., и эта разница не заметна, если только шары не выпущены с очень большой высоты. В то время разные люди выражали обеспокоенность идеями Галилея о падающих телах, утверждая, что будет невозможно различить небольшие различия во времени и расстоянии, необходимые для адекватной проверки идей Галилея, или сообщая, что эксперименты не согласуются с предсказаниями Галилея, или жалуясь на то, что для тщательной проверки идей Галилея не было подходящих высоких зданий с чистыми путями падения. Риччоли, напротив, смог показать, что он проводил повторяющиеся, последовательные и точные эксперименты в идеальном месте. Таким образом, как отмечает Д.Б. Мели,

Точные эксперименты Риччоли были широко известны во второй половине [семнадцатого] века и помогли прийти к консенсусу относительно эмпирической адекватности некоторых аспектов работы Галилея, особенно правила нечетных чисел и представления о том, что тяжелые тела падают с одинаковыми ускорениями и скоростями. не пропорционален весу. Его ограниченное согласие с Галилеем было значительным, поскольку оно исходило от несимпатичного читателя, который зашел так далеко, что включил текст осуждения Галилея в свои собственные публикации.

Работа о Луне

Карта Луны из Нового Альмагеста .

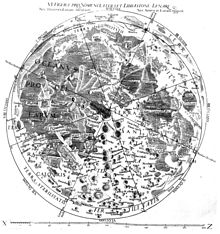
Риччоли и Гримальди тщательно изучали Луну, которую Гримальди рисовал карты. Этот материал вошел в 4-ю книгу « Нового Альмагеста» . Карты Гримальди были основаны на более ранних работах Иоганна Гевелия и Михаэля ван Лангрена . На одной из этих карт Риччоли дал названия лунным объектам — имена, которые легли в основу номенклатуры лунных объектов, которая используется до сих пор. Например, Mare Tranquillitatis (Море Спокойствия, место приземления Аполлона-11 в 1969 году) получило свое название от Риччоли. Риччоли назвал большие лунные области по погоде. Он назвал кратеры в честь выдающихся астрономов, сгруппировав их по философии и периодам времени. Хотя Риччоли отверг теорию Коперника, он назвал выдающийся лунный кратер «Коперник» , а другие важные кратеры он назвал в честь других сторонников теории Коперника, таких как Кеплер , Галилей и Лансбергиус . Поскольку кратеры, которые он и Гримальди назвали в честь себя, находятся в той же близости, что и эти, тогда как кратеры, названные в честь некоторых других астрономов-иезуитов, находятся в другой части Луны, рядом с очень выдающимся кратером, названным в честь Тихо Браге, лунная номенклатура Риччоли имеет время считалось молчаливым выражением симпатии к теории Коперника, которую он, как иезуит, не мог публично поддержать. Однако Риччоли сказал, что он погрузил всех коперниканцев в бурные воды ( Oceanus Procellarum ). Еще одной примечательной особенностью карты является то, что Риччоли включил в нее прямое заявление о том, что Луна необитаема. Это противоречило предположениям об обитаемой Луне, которые присутствовали в работах Николая Кузанского, Джордано Бруно и даже Кеплера и которые продолжались в работах более поздних писателей, таких как Бернар де Фонтенель и Уильям Гершель .

Аргументы относительно движения Земли

Фронтиспис «Нового Альмагеста» Риччоли 1651 года . Мифологические персонажи наблюдают небо в телескоп и сравнивают гелиоцентрическую теорию Коперника с его модифицированной версией геогелиоцентрической системы Тихо Браге, в которой Солнце, Луна, Юпитер и Сатурн вращаются вокруг Земли, а Меркурий, Венера и Марс вращается вокруг Солнца. Старая геоцентрическая теория Птолемея лежит заброшенной, устаревшей благодаря открытиям телескопа. Они показаны вверху и включают фазы Венеры и Меркурия, а также особенности поверхности Марса (слева), спутников Юпитера, колец Сатурна и особенности Луны (справа). Баланс склоняется в пользу системы «Тихоник» Риччоли.

Значительная часть « Нового Альмагеста» (9-я книга, состоящая из 343 страниц) посвящена анализу миросистемного вопроса: геоцентрична или гелиоцентрична Вселенная? Земля движется или неподвижна? Историк науки Эдвард Грант описал Книгу 9 как «вероятно, самый длинный, самый глубокий и авторитетный» анализ этого вопроса, сделанный «любым автором шестнадцатого и семнадцатого веков». по его мнению, очевидно, заменяя даже «Диалог Галилея о двух главных мировых системах — Птолемеевой и Коперниканской» . Действительно, один писатель недавно назвал Книгу 9 «книгой, которую должен был написать Галилей». В книге 9 Риччоли обсуждает 126 аргументов относительно движения Земли — 49 за и 77 против. Для Риччоли вопрос стоял не между геоцентрической мировой системой Птолемея и гелиоцентрической мировой системой Коперника, поскольку телескоп свергнул систему Птолемея; это было между геогелиоцентрической мировой системой, разработанной Тихо Браге в 1570-х годах. (в которой Солнце, Луна и звезды вращаются вокруг неподвижной Земли, а планеты вращаются вокруг Солнца – иногда называемая «геолиоцентрической» или «гибридной» системой) и система Коперника. Как показано на фронтисписе « Нового Альмагеста» (см. рисунок справа), Риччоли отдавал предпочтение модифицированной версии системы Тихо Браге; вот как он описал систему, которая «пришла [ему] на ум», когда он был в Парме: «она разделяет все с Тихоновой системой, кроме орбит Сатурна и Юпитера; для [мне] их центром было не Солнце, но сама Земля».

Многие авторы ссылаются на анализ Риччоли и 126 аргументов. Однако переводы аргументов « Нового Альмагеста» и обсуждение аргументов в любой степени более современными авторами редки: только для трех аргументов из 126 такие переводы и обсуждения легко доступны. Это, во-первых, аргумент, который Риччоли назвал «физико-математическим аргументом», который был связан с одной из гипотез Галилея; во-вторых, аргумент, основанный на том, что сегодня известно как « эффект Кориолиса »; в-третьих, аргумент, основанный на внешнем виде звезд, видимом в телескопы того времени.

«Физико-математический» аргумент

Риччоли обсуждает физико-математические аргументы в отношении аргументов как за, так и против движения Земли. 1632 года выдвинул гипотезу Галилей в своем «Диалоге» о том, что кажущееся линейное ускорение камня, падающего с башни, было результатом двух равномерных круговых движений, действующих совместно — суточного вращения Земли и второго равномерного кругового движения, принадлежащего камню и приобретшего чтобы его не унесло башней. Галилей говорит, что

[Т] истинное и реальное движение камня вообще никогда не ускоряется, но всегда равномерно и равномерно... Поэтому нам не нужно искать каких-либо других причин ускорения или каких-либо других движений для движущегося тела, независимо от того, остается ли оно на башне или при падении движется всегда одинаково; то есть по кругу, с той же скоростью и с той же равномерностью... если линия, описываемая падающим телом, не совсем такая, то она очень близка к ней... [и] согласно этим соображениям, прямая движение полностью исчезает, и природа вообще никогда им не пользуется.

Риччоли объяснил, что эта гипотеза не может работать: она не может применяться к падению тел вблизи полюсов Земли, где круговое движение, вызванное вращением Земли, будет незначительным или вообще отсутствовать; и даже на экваторе, где движение, вызванное вращением Земли, было бы больше, скорость падения, предсказанная идеей Галилея, была слишком медленной. Риччоли утверждал, что проблемы с гипотезой Галилея были признаком против мировой системы Коперника, но современные авторы расходятся во мнениях относительно рассуждений Риччоли по этому поводу.

Аргумент «эффекта Кориолиса»

Риччоли 1651 года, Иллюстрация из «Нового Альмагеста» показывающая, какое влияние должна оказывать вращающаяся Земля на снаряды. Когда из пушки стреляют по восточной цели B, пушка и цель движутся на восток с одинаковой скоростью, пока мяч находится в полете. Мяч попадает в цель так же, как если бы Земля была неподвижна. Когда пушка стреляет по северной цели Е, цель движется на восток медленнее, чем пушка и воздушное ядро, потому что в более северных широтах земля движется медленнее (вблизи полюса земля почти не движется). Таким образом, мяч следует по земле по изогнутой траектории, а не по диагонали, и попадает восточнее или правее мишени в точке G.

Риччоли также утверждал, что вращение Земли должно проявляться в полете артиллерийских снарядов, потому что на вращающейся Земле земля на разных широтах движется с разной скоростью. Он написал это

Если мяч выпущен по меридиану к полюсу (а не к востоку или западу), суточное движение приведет к уносу мяча [то есть траектория мяча будет отклонена), при прочих равных условиях: ибо на параллелях, расположенных ближе к полюсам, земля движется медленнее, тогда как на параллелях, расположенных ближе к экватору, земля движется быстрее.

Следовательно, если бы пушка, направленная прямо на цель на севере, выпустила шар, этот шар попал бы немного восточнее (справа) от цели благодаря вращению Земли. Но если бы пушка была выпущена на восток, отклонения не было бы, поскольку и пушка, и цель переместились бы на одинаковое расстояние в одном направлении. Риччоли говорил, что лучшие из канониров могут выстрелить снарядом прямо в жерло вражеской пушки; если бы этот эффект отклонения существовал при съемках на север, они бы его обнаружили. Риччоли утверждал, что отсутствие этого эффекта указывает на то, что Земля не вращается. Он был прав в своих рассуждениях в том, что эффект, который он описывает, действительно имеет место. Сегодня он известен как эффект Кориолиса в честь физика XIX века Гаспара-Гюстава Кориолиса (1792–1843). Однако правый отклонение действительно происходит независимо от того, в каком направлении направлена ​​пушка (для объяснения этого требуется гораздо более развитое понимание физики, чем то, что было доступно во времена Риччоли). В любом случае, эффект был слишком мал, чтобы канониры того времени могли его обнаружить.

Аргумент о размере звезды

Риччоли также использовал телескопические наблюдения звезд, чтобы опровергнуть теорию Коперника. Если смотреть в маленькие телескопы того времени, звезды выглядели как маленькие, но отчетливые диски. Эти диски были ложными – вызваны дифракцией волн света, попадающих в телескоп. Сегодня они известны как диски Эйри в честь астронома девятнадцатого века Джорджа Бидделла Эйри (1801–1892). Настоящие звездные диски, как правило, слишком малы, чтобы их можно было увидеть даже в лучшие современные телескопы. Но на протяжении большей части семнадцатого века считалось, что эти диски, видимые в телескоп, были настоящими телами звезд. Согласно теории Коперника, звезды должны были лежать на огромных расстояниях от Земли, чтобы объяснить, почему среди них не наблюдалось годового параллакса. Риччоли и Гримальди провели многочисленные измерения звездных дисков с помощью телескопа, предоставив подробное описание своей процедуры, чтобы любой желающий мог ее повторить. Затем Риччоли рассчитал физические размеры, которые должны были бы иметь измеренные звезды, чтобы они обе находились настолько далеко, насколько требовалось в теории Коперника, чтобы не было параллакса и чтобы размеры были видимы в телескоп. В результате во всех случаях звезды были огромными, затмевая Солнце. В некоторых сценариях одна-единственная звезда может превышать размер всей Вселенной, по оценкам геоцентриста, такого как Тихо Браге. Эта проблема, которую появление звезд в телескоп поставило перед теорией Коперника, была отмечена еще в 1614 году Симоном Мариусом, который сказал, что телескопические наблюдения за дисками звезд подтверждают теорию Тихона. Эту проблему признавали такие коперниканцы, как Мартин ван ден Хове (1605–1639), который также измерил диски звезд и признал, что проблема огромных размеров звезд может заставить людей отвергнуть теорию Коперника.

Другие аргументы

Другие аргументы, представленные Риччоли в девятой книге « Нового Альмагеста», были разнообразными. Были споры относительно того, смогут ли здания стоять или птицы смогут летать, если Земля вращается; какие движения естественны для тяжелых предметов; что представляет собой более простое и элегантное небесное устройство; было ли небо или Земля более приспособлены для движения и более легко и экономично перемещались; был ли центр вселенной более или менее благородным положением; и многие другие. Многие антикоперниканские аргументы в « Новом Альмагесте» имели корни в антикоперниканских аргументах Тихо Браге.

Риччоли энергично выступал против системы Коперника и даже охарактеризовал некоторые аргументы в пользу неподвижности Земли как неопровержимые. Однако он также опроверг некоторые антикоперниканские аргументы, приняв сторону коперниканцев в своих утверждениях о том, что вращение Земли не обязательно будет ощущаться, что оно не разрушит здания и не оставит птиц. Некоторые авторы предполагают, что Риччоли, возможно, был тайным коперниканецом, которому в силу своего положения иезуита приходилось притворяться, что он выступает против этой теории.

Astronomia Reformata ( Реформатская астрономия )

Другой выдающейся астрономической публикацией Риччоли была его Astronomia Reformata ( «Реформатская астрономия» ) 1665 года — еще один большой том, хотя и составлявший лишь половину « Нового Альмагеста» . Содержание этих двух существенно пересекается; Реформатскую астрономию можно рассматривать как сокращенную и обновленную версию Нового Альмагеста .

Риччоли 1665 года . из реформатской астрономии Представления об изменении внешнего вида Сатурна

« Реформированная астрономия» содержит обширный отчет об изменении внешнего вида Сатурна. В раздел, посвященный Юпитеру, включены очевидные записи очень раннего (если не самого раннего) Наблюдение Большого Красного Пятна Юпитера , сделанное Леандером Бандтиусом, аббатом Дунисбурга и владельцем особенно прекрасного телескопа, в конце 1632 года. Также в этот раздел Риччоли включает сообщения о появлении и исчезновении поясов облаков Юпитера с течением времени.

Появление физико-математического аргумента в реформатской астрономии стало поводом для Стефано дельи Анджели (1623–1697) предпринять «неожиданную, несколько неуважительную, а иногда и легкомысленную атаку». о Риччоли и споре. Джеймс Грегори опубликовал в Англии в 1668 году отчет о возникшем публичном и личном споре по поводу падающих предметов. Это было прелюдией к Роберта Гука приглашению (1635–1703) Исааку Ньютону (1642–1727) возобновить научную переписку с Королевским обществом и к их последующей дискуссии о траектории падения тел, «которая отвлекла внимание Ньютона». от «прочих дел» и обратно к изучению земной и небесной механики». Реформированная астрономия представляла собой адаптацию к накапливающимся данным наблюдений в пользу эллиптической небесной механики Иоганна Кеплера: она включила эллиптические орбиты в геогелиоцентрическую теорию Тихона. Риччоли принял идеи Кеплера, но остался противником гелиоцентрической теории. Действительно, после спора с Анджели отношение Риччоли к гелиоцентризму ужесточилось.

Другая работа

Между 1644 и 1656 годами Риччоли занимался топографическими измерениями, работая с Гримальди, определяя значения окружности Земли и соотношения воды и суши. Однако дефекты метода дали менее точные значения градусов дуги меридиана, чем Снеллиус, полученный несколькими годами ранее. Снеллиус ошибся примерно на 4000 метров; но Риччоли ошибся более чем на 10 000 метров. Риччоли нашёл 373 000 педов, несмотря на то, что ссылки на римскую степень в древности всегда составляли 75 миллиариев или 375 000 педов.

Ему часто приписывают то, что он был одним из первых, кто наблюдал в телескоп звезду Мицар и отметил, что это двойная звезда ; однако Кастелли и Галилей наблюдали это гораздо раньше.

По словам Альфредо Диниса,

Риччоли пользовался большим авторитетом и большой оппозицией как в Италии, так и за рубежом, не только как человек энциклопедических знаний, но и как человек, который мог понимать и обсуждать все актуальные вопросы космологии, наблюдательной астрономии и географии того времени.

Избранные произведения

Произведения Риччоли написаны на латыни .

Астрономия

Устройство и использование географического креста для изображения с удивительной легкостью всех дней и ночей восхода и захода солнца, а также разнообразия всех часов , 1643 г.

• Устройство географического креста и его использование для изображения… всех дней и ночей восхода и захода солнца (Феррони: 1643 г.) ( Карта мира из Галлики )
• Устройство и использование географического креста для изображения с удивительной легкостью всех дней и ночей восхода и захода солнца, а также разнообразия всех часов (на латыни). Болонья: Джованни Баттиста Феррони. 1643 г.
• Новый астрономический альмагестум, включающий старые и новые наблюдения других людей и продвигаемый его собственными новыми теоремами, проблемами и таблицами (том I–III, 1651 г.) (Или: Том 1: первая часть в Google Книгах ; вторая часть в Google Книгах )
• Geographiae et Hydrographiae reformatae libri duodecim в Google Книгах , Болонья, 1661 г.
  • Реформированная география и гидрография: двенадцать книг, недавно переработанных и дополненных в Google Книгах . 2-е изд., Венеция, 1672. 695 с.
• реформатская астрономия (т. I – II, 1665 г.)
  • Том 1 в Google Книгах : наблюдения, гипотезы и объяснения.
  • Том 2 в Google Книгах : инструкции по использованию и 102 таблицы.
• Месть григорианского календаря Фрэнсису Леверу (1666 г.)
• Физико-математический аргумент против суточного движения Земли (на итальянском языке). Болонья: Эмилио Мария Манолесси и братья. 1668.
• Извинения РП Ио. Крещение. Общество Иисуса Риччоли за физико-математический аргумент против системы Коперника (1669 г.)
• Хронологии реформированы и сведены к определенным выводам... (Т. I-IV, 1669 г.)
  • ... первый том, содержащий доктрину времени, в Google Books , 404 стр.
  • ... второй том «Эпохи мира и три хроники, содержащие его» в Google Books , 236 стр.
  • ... третий том, содержащий многочисленные каталоги известных людей и вещей с указанием их дат, в Google Книгах, 161 стр. и четвертый том 324 стр.
• Карта широт и долгот (1689 г.)
• Карта широты и долготы (на испанском языке). Кордова: Антонио Серрано. 1744 г.

Теология

• Уникальное Евангелие Господа нашего Иисуса Христа, составленное из слов четырёх евангелистов и распространяемое в медитациях в Google Books . Болонья, 1667, 466 с.
• Иммунитет как от теоретической, так и от практической ошибки в определениях ст. Апостольский престол в канонизации святых, в установлении церковных праздников и в решении догматов, которые традиционно лишь косвенно содержатся в письменном слове Божием или в достаточной степени вытекают друг из друга , Болонья, 1668 г. (перечислены в Индекс запрещенных книг 1669 г. )
• Философско-богословский трактат о различиях существ в Боге и в тварях (1669 г.)

Избранные издания книг Риччоли о просодии.

Книги Риччоли о просодии неоднократно перерабатывались и выдержали множество изданий.

• Prosodia Bonnoniensis переформатированная ... . Болонь, 1655 г.
• Reformata Prosodia Bononiensis в Google Книгах . Падуя, 1714 г. (два тома объединены в один)

См. также

• Список ученых-иезуитов
• Список римско-католических ученых-священнослужителей
• Гримальди (кратер)
• завитки (кратер)

Примечания

• Питер, Баркер. «Воксканис» . Проверено 29 ноября 2018 г.

Ссылки

• AlunSalt: «Коперник и звезда, которая была больше Вселенной» (17 января 2011 г.)
• Грейни, Кристофер М. (2011). «126 аргументов относительно движения Земли, представленные Джованни Баттистой Риччоли в его Almagestum Novum 1651 года». arXiv : 1103.2057 [ physical.hist-ph ].
• BBC News 2010: «Коричневая полоса Юпитера возвращается, говорят астрономы» (26 ноября 2010 г.)
• Болт, Марвин (редактор) 2007, Картирование Вселенной (Чикаго: Планетарий Адлера и Музей астрономии)
•  Брок, Генри Матиас (1912). « Джованни Баттиста Риччоли ». В Герберманне, Чарльз (ред.). Католическая энциклопедия . Том. 13. Нью-Йорк: Компания Роберта Эпплтона.
• Кэмпбелл, Томас Джозеф 1921, Иезуиты, 1534–1921: история Общества Иисуса от его основания до настоящего времени (Нью-Йорк: Энциклопедия Пресс)
• Коминс, Н. Ф. и Кауфманн, У. Дж. 2009, Открытие Вселенной: от звезд до планет (Нью-Йорк: WH Freeman)
• Кроу, MJ 2008 Дебаты о внеземной жизни, от древности до 1915 года: справочник (University of Notre Dame Press)
• Деламбр JBJ 1821, История современной астрономии (Париж)
• Диалог о двух главных мировых системах , 2001 г., Галилео Галилей [1632], переведенный и с исправленными примечаниями Стиллмана Дрейка и предисловием Альберта Эйнштейна (Нью-Йорк: Random House / The Modern Library)
• Discover News 2011: «Открыл ли Риччоли эффект Кориолиса?» Архивировано 7 октября 2012 г. в Wayback Machine , Дженнифер Уэллетт (27 января 2011 г.).
• Динис, Альфредо 2002, «Был ли Риччоли тайным коперниканец?» в « Джамбаттиста Риччоли и научные заслуги иезуитов в эпоху барокко » под редакцией Марии Терезы Боргато (Флоренция: Лео С. Ольшки), 49–77.
• Динис, Альфредо 2003, «Джованни Баттиста Риччоли и наука его времени» в журнале «Иезуитская наука и республика литературы» , стр. 195, в Google Книгах , под редакцией Мордехая Фейнгольда (Кембридж, Массачусетс: MIT Press), 195–224 (значительные выдержки)
• Галлоуэй, Т. 1842, Замечания о мере Фернеля степени , с. 90, в Google Книгах , Философском журнале и научном журнале , том 20, 90–98.
• Джинджерич, Оуэн 1973, «Коперник и Тихо», Scientific American , том 229, 86–101.
• Грейни, Кристофер М. (2010). «Телескоп против Коперника: наблюдения Риччоли за звездами в поддержку геоцентрической Вселенной». Журнал истории астрономии . 41 (4): 453. Бибкод : 2010JHA....41..453G . дои : 10.1177/002182861004100402 . S2CID   117782745 .
• Грейни, Кристофер М. (2010). «Изменения в облачных поясах Юпитера, 1630–1664 гг., Как сообщается в Astronomia Reformata 1665 г. Джованни Баттиста Риччоли». Балтийская астрономия . 19 (3–4): 265. arXiv : 1008.0566 . Бибкод : 2010БалтА..19..265Г . дои : 10.1515/astro-2017-0425 .
• Грейни, Кристофер М. (2011). «Эффект Кориолиса, за два столетия до Кориолиса». Физика сегодня . 64 (8): 8–9. Бибкод : 2011PhT....64h...8G . дои : 10.1063/PT.3.1195 . S2CID   121193379 .
• Грейни, Кристофер М.; Грейсон, Тимоти П. (2011). «О телескопических дисках звезд: обзор и анализ звездных наблюдений с начала семнадцатого до середины девятнадцатого веков». Анналы науки . 68 (3): 351–373. arXiv : 1003.4918 . дои : 10.1080/00033790.2010.507472 . S2CID   118007707 .
• Грейни, Кристофер М. (2012). «Анатомия падения: Джованни Баттиста Риччоли и история г ». Физика сегодня . 65 (9): 36–40. Бибкод : 2012ФТ....65и..36Г . дои : 10.1063/PT.3.1716 .
• Грейни, КМ, 2015 г., Отказ от всякой власти: Джованни Баттиста Риччоли и наука против Коперника в эпоху Галилея , University of Notre Dame Press, ISBN   978-0268029883
• Грант, Эдвард 1984, «В защиту централизации и неподвижности Земли: схоластическая реакция на коперниканство в семнадцатом веке», Труды Американского философского общества , новая серия, том 74, 1–69.
• Грант, Эдвард 1996, Планеты, звезды и сферы: Средневековый космос, 1200–1687 (Кембридж: издательство Кембриджского университета)
• Хейлброн, Дж. Л. 1999, Солнце в церкви: соборы как солнечные обсерватории (Кембридж, Массачусетс: издательство Гарвардского университета)
• Хёфер, Фердинанд 1873, История астрономии (Париж)
• Койре, Александр (1955). «Документальная история проблемы падения от Кеплера до Ньютона: о движении естественно падающих гравитационных частиц в гипотезе движущейся Земли». Труды Американского философского общества . 45 (4): 329–395. дои : 10.2307/1005755 . JSTOR   1005755 .
• Мели, Доменико Бертолони 2006, Мышление объектами: трансформация механики в семнадцатом веке (Балтимор, Мэриленд: издательство Университета Джонса Хопкинса)
• New Scientist 2010: «Юпитер теряет полосу» , Дэвид Шига (11 мая 2010 г.)
• New Scientist 2011: «Эффект Кориолиса обнаружен за 184 года до Кориолиса» , МакГрегор Кэмпбелл (14 января 2011 г.); «Силы и судьба», New Scientist (печатное издание от 8 января 2011 г.), 6
• Рафаэль, Рене 2011, «Неастрономическое изображение в астрономическом тексте: визуализация движения в Almagestum Novum Риччоли », Журнал истории астрономии , том 42, 73–90
• Ролик TOF: «Книга, которую должен был написать Галилей» (21 апреля 2011 г.)
• Ван Хелден, Альберт 1984, «Галилей, телескопическая астрономия и система Коперника», в «Всеобщей истории астрономии » под редакцией М. А. Хоскина, том 2A (Кембридж: Cambridge University Press)
• Уитакер, Э.А. 1999, Картирование и наименование Луны: история лунной картографии и номенклатуры (издательство Кембриджского университета)
• Ф. Маркаччи, Противоречивое небо: Джованни Баттиста Риччоли и система третьего мира , Модена-Перуджа, Академия наук-Агуаплано, 2018.
• Маркаччи, Флавия (2023). «Геогелиоцентрическое использование Эпицепициклов , эллипсов и спиралей ГБ Риччоли». Журнал истории астрономии . 54 (2): 171–192. Бибкод : 2023JHA....54..171M . дои : 10.1177/00218286231165331 . S2CID   258548319 .
• Маркаччи, Флавия (2018). «Наука и абсолютная гипотеза. Методология и логика исследования в « Almagestum Новом » Джованни Баттисты Риччоли ». Международные архивы истории наук . 68 (180–181): 72–107. дои : 10.1484/J.ARIHS.5.120152 .
• Маркаччи, Флавия (2021). «Взгляд с первого взгляда». Нунций . 36 : 119–142. дои : 10.1163/18253911-bja10010 . S2CID   233568069 .

Внешние ссылки

• медиафайлы по теме: Джованни Риччоли. Викискладе есть
• Краткая биография Риччоли из Католической энциклопедии .
• Факты о Риччоли из Университета Райса . проекта Галилео
• Риччоли, Иоанн Креститель (французский)
• Альмагестум новой астрономии в формате PDF