Кубическая гармоника

Кубические гармоники

В таких областях, как вычислительная химия и физика твердого тела и конденсированного состояния , так называемые атомные орбитали или спин-орбитали , как они появляются в учебниках. по квантовой физике, часто частично заменяются кубическими гармониками по ряду причин. Эти гармоники обычно называют тессеральными гармониками в области физики конденсированного состояния, в которой название «кубические гармоники» скорее относится к неприводимым представлениям в кубической точечной группе.

Введение

The $2l+1$ водородоподобные атомные орбитали с главным квантовым числом $n$ и квантовое число углового момента $l$ часто выражаются как

$\psi _{nlm}(\mathbf {r} )=R_{nl}(r)Y_{l}^{m}(\theta ,\varphi )$

в котором $R_{nl}(r)$ — радиальная часть волновой функции и $Y_{l}^{m}(\theta ,\varphi )$ – угловая зависимая часть. $Y_{l}^{m}(\theta ,\varphi )$ являются сферическими гармониками , которые являются решениями оператора углового момента . Сферические гармоники являются представлениями функций группы полного вращения SO(3) с вращательной симметрией. Во многих областях физики и химии эти сферические гармоники заменяются кубическими гармониками, потому что вращательная симметрия атома и его окружения искажается или потому, что кубические гармоники дают вычислительные преимущества.

Симметрия и система координат

Во многих случаях, особенно в химии , физике твердого тела и конденсированного состояния , исследуемая система не обладает вращательной симметрией. Часто он имеет какую-то более низкую симметрию с особым представлением точечной группы или вообще не имеет пространственной симметрии . Биологические и биохимические системы, такие как аминокислоты и ферменты, часто принадлежат к точечным группам с низкой молекулярной симметрией . Твердые кристаллы элементов часто относятся к пространственным группам и точечным группам с высокой симметрией. (Представления кубических гармоник часто перечисляются и упоминаются в таблицах групп точек .) Система имеет, по крайней мере, фиксированную ориентацию в трехмерном евклидовом пространстве . Поэтому система координат, которая используется в таких случаях, чаще всего представляет собой декартову систему координат, а не сферическую систему координат . В декартовой системе координат атомные орбитали часто выражаются как

$\psi _{nlc}(\mathbf {r} )=R_{nl}(r)X_{lc}(\mathbf {r} )$

с кубическими гармониками , $X_{lc}(\mathbf {r} )$, в качестве базового набора . В расчетах LCAO и MO в вычислительной химии или расчетах сильной связи в физике твердого тела кубические гармоники используются в качестве основы атомных орбит. Индексы lc обозначают некоторое декартово представление.

Базовые преобразования

Для представления сферических гармоник выбрана сферическая система координат с главной осью в направлении z . Для кубических гармоник эта ось также является наиболее удобным выбором. Для состояний с более высоким квантовым числом углового момента $l$ и более высокое измерение $l(l+1)$ число возможных вращений или базисных преобразований в гильбертовом пространстве растет, а вместе с ним и число возможных ортогональных представлений, которые можно построить на основе $l(l+1)$базисный набор -мерных сферических гармоник. Существует больше свободы в выборе представления, которое соответствует симметрии точечной группы задачи. Кубические представления, перечисленные в таблице, являются результатом преобразований, которые представляют собой двумерный поворот на 45 ° и поворот на 90 ° к реальной оси, если это необходимо, например

$X_{lc}(\mathbf {r} )=Y_{l}^{0}$

$X_{lc'}(\mathbf {r} )={\frac {1}{i^{n_{c'}}{\sqrt {2}}}}\left(Y_{l}^{m}-Y_{l}^{-m}\right)$

$X_{lc''}(\mathbf {r} )={\frac {1}{i^{n_{c''}}{\sqrt {2}}}}\left(Y_{l}^{m}+Y_{l}^{-m}\right)$

Значительное количество сферических гармоник занесено в Таблицу сферических гармоник .

Вычислительные преимущества

Ион феррицианида , используемый для получения «синего цвета Тернбулла» с октаэдрически окруженным центральным Fe. ³⁺ -ион.

Прежде всего, кубические гармоники являются вещественными функциями , а сферические гармоники — комплексными функциями . Комплексные числа двумерны и имеют действительную и мнимую части. Комплексные числа предлагают очень красивые и эффективные инструменты для аналитического решения математических задач, но они не очень эффективны, когда используются для численных расчетов. Пропуск мнимой части экономит половину вычислительных усилий при суммировании, в четыре раза при умножении и часто в восемь или даже больше раз, когда дело доходит до вычислений с использованием матриц.

Кубические гармоники часто соответствуют симметрии потенциала или окружения атома. Обычное окружение атомов в твердых телах и химических комплексах представляет собой октаэдрическое окружение с симметрией октаэдрической кубической точечной группы . Представления кубических гармоник часто обладают высокой симметрией и множественностью, поэтому такие операции, как интегрирование, можно свести к ограниченной или неприводимой части области определения функции, которую необходимо вычислить. Задачу с 48-кратной октаэдрической _{симметрией Oh} можно вычислить гораздо быстрее, если ограничить вычисление, например интегрирование, неприводимой частью области определения функции.

Таблица кубических гармоник

S-орбитали

имеют S-орбитали только радиальную часть.

$\psi _{n00}(\mathbf {r} )=R_{n0}(r)Y_{0}^{0}$

$s=X_{00}=Y_{0}^{0}={\frac {1}{\sqrt {4\pi }}}$

	п=1	2	3	4	5	6	7
Р н0

P-орбитали

Три p-орбитали представляют собой атомные орбитали с квантовым числом углового момента ℓ = 1 . Кубическое гармоническое выражение p-орбиталей

$p_{z}=N_{1}^{c}{\frac {z}{r}}=Y_{1}^{0}$

$p_{x}=N_{1}^{c}{\frac {x}{r}}={\frac {1}{\sqrt {2}}}\left(Y_{1}^{-1}-Y_{1}^{1}\right)$

$p_{y}=N_{1}^{c}{\frac {y}{r}}={\frac {i}{\sqrt {2}}}\left(Y_{1}^{-1}+Y_{1}^{1}\right)$

с

$N_{1}^{c}=\left({\frac {3}{4\pi }}\right)^{1/2}$

п з	п х	п да

D-орбитали

Пять d-орбиталей представляют собой атомные орбитали с квантовым числом углового момента ℓ = 2 . Угловая часть d-орбиталей часто выражается как

$\psi _{n2c}(\mathbf {r} )=R_{n2}(r)X_{2c}(\mathbf {r} )$

Угловая часть d-орбиталей представляет собой кубические гармоники $X_{2c}(\mathbf {r} )$

$d_{z^{2}}=N_{2}^{c}{\frac {3z^{2}-r^{2}}{2r^{2}{\sqrt {3}}}}=Y_{2}^{0}$

$d_{xz}=N_{2}^{c}{\frac {xz}{r^{2}}}={\frac {1}{\sqrt {2}}}\left(Y_{2}^{-1}-Y_{2}^{1}\right)$

$d_{yz}=N_{2}^{c}{\frac {yz}{r^{2}}}={\frac {i}{\sqrt {2}}}\left(Y_{2}^{-1}+Y_{2}^{1}\right)$

$d_{xy}=N_{2}^{c}{\frac {xy}{r^{2}}}={\frac {i}{\sqrt {2}}}\left(Y_{2}^{-2}-Y_{2}^{2}\right)$

$d_{x^{2}-y^{2}}=N_{2}^{c}{\frac {x^{2}-y^{2}}{2r^{2}}}={\frac {1}{\sqrt {2}}}\left(Y_{2}^{-2}+Y_{2}^{2}\right)$

с

$N_{2}^{c}=\left({\frac {15}{4\pi }}\right)^{1/2}$

д з 2	д хз	д трек	д ху	д х 2 -и 2

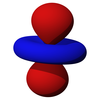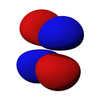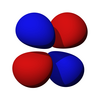f-орбитали

Семь f-орбиталей представляют собой атомные орбитали с квантовым числом углового момента ℓ = 3 . часто выражается как

$\psi _{n3c}(\mathbf {r} )=R_{n3}(r)X_{3c}(\mathbf {r} )$

Угловая часть f-орбиталей представляет собой кубические гармоники $X_{3c}(\mathbf {r} )$. Во многих случаях для построения кубического базисного набора f-орбиталей выбираются различные линейные комбинации сферических гармоник.

$f_{z^{3}}=N_{3}^{c}{\frac {z(2z^{2}-3x^{2}-3y^{2})}{2r^{3}{\sqrt {15}}}}=Y_{3}^{0}$

$f_{xz^{2}}=N_{3}^{c}{\frac {x(4z^{2}-x^{2}-y^{2})}{2r^{3}{\sqrt {10}}}}={\frac {1}{\sqrt {2}}}\left(Y_{3}^{-1}-Y_{3}^{1}\right)$

$f_{yz^{2}}=N_{3}^{c}{\frac {y(4z^{2}-x^{2}-y^{2})}{2r^{3}{\sqrt {10}}}}={\frac {i}{\sqrt {2}}}\left(Y_{3}^{-1}+Y_{3}^{1}\right)$

$f_{xyz}=N_{3}^{c}{\frac {xyz}{r^{3}}}={\frac {i}{\sqrt {2}}}\left(Y_{3}^{-2}-Y_{3}^{2}\right)$

$f_{z(x^{2}-y^{2})}=N_{3}^{c}{\frac {z\left(x^{2}-y^{2}\right)}{2r^{3}}}={\frac {1}{\sqrt {2}}}\left(Y_{3}^{-2}+Y_{3}^{2}\right)$

$f_{x(x^{2}-3y^{2})}=N_{3}^{c}{\frac {x\left(x^{2}-3y^{2}\right)}{2r^{3}{\sqrt {6}}}}={\frac {1}{\sqrt {2}}}\left(Y_{3}^{-3}-Y_{3}^{3}\right)$

$f_{y(3x^{2}-y^{2})}=N_{3}^{c}{\frac {y\left(3x^{2}-y^{2}\right)}{2r^{3}{\sqrt {6}}}}={\frac {i}{\sqrt {2}}}\left(Y_{3}^{-3}+Y_{3}^{3}\right)$

с

$N_{3}^{c}=\left({\frac {105}{4\pi }}\right)^{1/2}$

ж ж 3	ж хз 2	ж ыз 2	xyz ж	f z(x 2 -и 2 )	f х(х 2 -3 года 2 )	f y(3x 2 -и 2 )

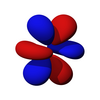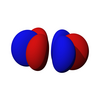См. также

• Атомные орбитали
• Атомная физика
• Сферические гармоники
• Сферическая система координат
• Декартова система координат
• Евклидово пространство
• Гильбертово пространство
• Базовый набор (химия)
• Базис (линейная алгебра)
• Координатный вектор
• метод ЛКАО
• Метод жесткого связывания