Последовательность с низким расхождением
В математике последовательность с низким расхождением — это последовательность , обладающая тем свойством, что для всех значений N ее подпоследовательность x 1 , ..., x N имеет низкую невязку .
Грубо говоря, расхождение последовательности мало, если доля точек последовательности, попадающих в произвольное множество B , близка к пропорциональной мере B , как это происходило бы в среднем (но не для отдельных выборок) в случае последовательность равнораспределенная . Конкретные определения расхождения различаются в зависимости от выбора B ( гиперсферы , гиперкубы и т. д.) и того, как расхождение для каждого B вычисляется (обычно нормализуется) и комбинируется (обычно путем принятия наихудшего значения).
Последовательности с низким расхождением также называются квазислучайными последовательностями из-за их общего использования в качестве замены равномерно распределенных случайных чисел . Модификатор «квази» используется для более четкого обозначения того, что значения последовательности с низким расхождением не являются ни случайными, ни псевдослучайными , но такие последовательности имеют некоторые общие свойства случайных величин, а в некоторых приложениях, таких как метод квази-Монте-Карло, их меньшее несоответствие. является важным преимуществом.
Приложения
[ редактировать ]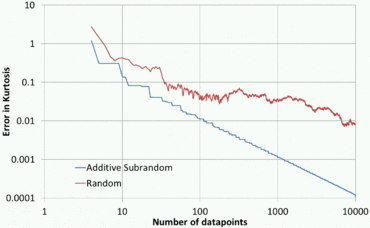
Квазислучайные числа имеют преимущество перед чисто случайными числами в том, что они быстро и равномерно покрывают интересующую область.
Двумя полезными приложениями являются поиск характеристической функции функции плотности вероятности и поиск производной функции детерминированной функции с небольшим количеством шума. более высокого порядка моменты Квазислучайные числа позволяют очень быстро рассчитывать с высокой точностью.
Приложениями, не использующими сортировку, могут быть поиск среднего значения , стандартного отклонения , асимметрии и эксцесса статистического распределения, а также поиск интегральных и глобальных максимумов и минимумов сложных детерминированных функций. Квазислучайные числа также можно использовать в качестве отправной точки для детерминированных алгоритмов, которые работают только локально, таких как итерация Ньютона-Рафсона .
Квазислучайные числа также можно комбинировать с алгоритмами поиска. С помощью алгоритма поиска квазислучайные числа можно использовать для нахождения режима , медианы , доверительных интервалов и кумулятивного распределения статистического распределения, а также всех локальных минимумов и всех решений детерминированных функций.
Последовательности с малым расхождением в численном интегрировании
[ редактировать ]Различные методы численного интегрирования можно сформулировать как аппроксимацию интеграла функции f в некотором интервале, например [0,1], как среднего значения функции, вычисленной в наборе { x 1 , ..., x N } в этом интервал:
Если точки выбраны как x i = i / N , это правило прямоугольника . Если точки выбраны случайным (или псевдослучайным ) распределением, это метод Монте-Карло . Если точки выбираются как элементы последовательности с малым расхождением, это и есть метод квази-Монте-Карло . Замечательный результат — неравенство Коксмы–Главки (приведенное ниже) показывает, что погрешность такого метода может быть ограничена произведением двух слагаемых, одно из которых зависит только от f , а другое — невязка множества { х 1 , ..., х N }.
Удобно построить набор { x 1 , ..., x N } таким образом, что если набор из N построен +1 элементов, предыдущие N элементов не нужно пересчитывать. Правило прямоугольника использует набор точек, которые имеют небольшое расхождение, но обычно элементы необходимо пересчитывать, если N увеличивается. Элементы не нужно пересчитывать случайным методом Монте-Карло, если N увеличивается, но наборы точек не имеют минимального расхождения. Используя последовательности с низким расхождением, мы стремимся к малому расхождению и отсутствию необходимости в повторных вычислениях, но на самом деле последовательности с низким расхождением могут быть только постепенно эффективными в отношении несоответствий, если мы не допускаем повторных вычислений.
Определение расхождения
[ редактировать ]Невязка 1 набора P = { x как , ..., x N } определяется с использованием Нидеррайтера обозначений
где λ s – s -мерная мера Лебега , A ( B ; P ) — количество точек из P , попадающих в B , — J множество s- мерных интервалов или ящиков вида
где .
Звездное несоответствие D * N ( P ) определяется аналогично, за исключением того, что верхняя грань берется по множеству J * прямоугольных коробок формы
где u i находится в полуинтервале [0, 1).
Эти два связаны
Примечание. Согласно этим определениям, несоответствие представляет собой наихудшее или максимальное отклонение плотности точек однородного набора. Однако имеют значение и другие меры ошибок, что приводит к другим определениям и мерам вариации. Например, расхождение L2 или модифицированное центрированное расхождение L2 также интенсивно используются для сравнения качества однородных наборов точек. И то, и другое гораздо проще вычислить при больших N и s.
Неравенство Коксмы–Профита.
[ редактировать ]Пусть я с быть s -мерным единичным кубом, Я с = [0, 1] × ... × [0, 1]. Пусть f имеет ограниченную вариацию V ( f ) на Ī с в смысле Харди и Краузе. Тогда для любого x 1 , ..., x N во мне с = [0, 1) × ... × [0, 1),
Неравенство Коксмы I – Главки является точным в следующем смысле: для любого множества точек { 1 , ..., x N } в x с и любой , существует функция f с ограниченной вариацией и V ( f ) = 1 такая, что
Поэтому качество правила численного интегрирования зависит только от невязки D * Н ( х 1 ,..., х Н ).
Формула Фри-Зарембы
[ редактировать ]Позволять . Для мы писать
и обозначим через точка, полученная из x заменой координаты не тебе в . Затем
где – функция несоответствия.
Л 2 вариант неравенства Коксмы – Профита
[ редактировать ]Применяя неравенство Коши–Шварца для интегралов и сумм к тождеству Главки–Зарембы, получаем вариант неравенства Коксмы – Профита:
где
и
Расхождение имеет большое практическое значение, поскольку для данного набора точек возможны быстрые явные вычисления. Таким образом, можно легко создавать оптимизаторы набора точек, используя несоответствие как критерий.
Неравенство Эрдеша–Турана–Коксмы
[ редактировать ]Трудно с вычислительной точки зрения найти точное значение невязки больших наборов точек. Неравенство Эрдеша – – Турана . Коксмы дает верхнюю границу
Пусть x 1 ,..., x N — точки в I с и H — произвольное положительное целое число. Затем
где
Основные предположения
[ редактировать ]Гипотеза 1. Существует константа cs , зависящая только от размерности s , такая, что
для любого конечного множества точек { x 1 ,..., x N }.
Гипотеза 2. Существует константа c ' s зависит только от s , такого, что
для бесконечного числа N для любой бесконечной последовательности x 1 , x 2 , x 3 ,....
Эти предположения эквивалентны. они были доказаны Для s ≤ 2 В.М. Шмидтом . В более высоких измерениях соответствующая проблема все еще остается открытой. Наиболее известные нижние оценки принадлежат Майклу Лэйси и его сотрудникам.
Нижние границы
[ редактировать ]Пусть s = 1. Тогда
для любого конечного множества точек { x 1 , ..., x N }.
Пусть s = 2. В.М. Шмидт доказал, что для любого конечного множества точек { x 1 , ..., x N }
где
Для произвольных размерностей s > 1 К. Ф. Рот доказал, что
для любого конечного множества точек { x 1 , ..., x N }. Йозеф Бек [1] установили двойное логарифмическое улучшение этого результата в трех измерениях. Это было улучшено Д. Билыком и М. Т. Лейси до степени одиночного логарифма. Самая известная оценка для s > 2 обусловлена Д. Билык и М.Т. Лейси и А. Вагаршакян. [2] Для s > 2 существует такое t > 0, что
для любого конечного множества точек { x 1 , ..., x N }.
Построение последовательностей с низким расхождением
[ редактировать ]Поскольку любое распределение случайных чисел может быть отображено на равномерное распределение, а квазислучайные числа отображаются таким же образом, эта статья касается только генерации квазислучайных чисел на многомерном равномерном распределении.
Известны конструкции последовательностей такие, что
где C — некоторая константа, зависящая от последовательности. После гипотезы 2 считается, что эти последовательности имеют наилучший возможный порядок сходимости. Ниже приведены примеры последовательности Ван дер Корпута , последовательности Холтона и последовательности Соболя . Одним из общих ограничений является то, что методы построения обычно могут гарантировать только порядок сходимости. Практически, низкое расхождение может быть достигнуто только в том случае, если N достаточно велико, а при больших заданных s этот минимум N может быть очень большим. Это означает, что выполнение анализа Монте-Карло, например, с s=20 переменными и N=1000 точками с помощью генератора последовательностей с низким расхождением, может дать лишь очень незначительное улучшение точности. [ нужна ссылка ] .
Случайные числа
[ редактировать ]Последовательности квазислучайных чисел можно генерировать из случайных чисел, налагая на эти случайные числа отрицательную корреляцию. Один из способов сделать это — начать с набора случайных чисел. на и построить квазислучайные числа которые однородны по с использованием:
для странный и для даже.
Второй способ сделать это с начальными случайными числами — построить случайное блуждание со смещением 0,5, как показано ниже:
То есть возьмите предыдущее квазислучайное число, добавьте 0,5 и случайное число и возьмите результат по модулю 1.
Для более чем одного измерения можно использовать латинские квадраты соответствующего размера для обеспечения смещения, чтобы обеспечить равномерное покрытие всей области.

Аддитивная повторяемость
[ редактировать ]Для любого иррационального , последовательность
имеет несоответствие, имеющее тенденцию к . Обратите внимание, что последовательность может быть определена рекурсивно с помощью
Хорошее соотношение цены и качества дает меньшее расхождение, чем последовательность независимых однородных случайных чисел.
Расхождение может быть ограничено аппроксимации показателем . Если показатель аппроксимации равен , то для любого , имеет место следующая оценка: [3]
По теореме Туэ-Зигеля-Рота показатель аппроксимации любого иррационального алгебраического числа равен 2, что дает оценку выше.
Приведенное выше рекуррентное соотношение похоже на рекуррентное соотношение, используемое линейным конгруэнтным генератором — генератором псевдослучайных чисел низкого качества: [4]
Для аддитивной повторяемости с низким расхождением, описанной выше, a и m выбраны равными 1. Однако обратите внимание, что это не приведет к генерации независимых случайных чисел, поэтому их не следует использовать для целей, требующих независимости.
Стоимость с наименьшим расхождением является дробная часть золотого сечения : [5]
Другая величина, которая почти так же хороша, — это дробная часть отношения серебра , которая представляет собой дробную часть квадратного корня из 2:
В более чем одном измерении для каждого измерения необходимы отдельные квазислучайные числа. Удобный набор используемых значений — это квадратные корни простых чисел от двух и выше, взятые по модулю 1:
Однако было показано, что набор значений, основанный на обобщенном золотом сечении, дает более равномерно распределенные точки. [6]
В списке генераторов псевдослучайных чисел перечислены методы генерации независимых псевдослучайных чисел. Примечание. В небольшом количестве измерений рекурсивная рекурсия приводит к однородным наборам хорошего качества, но для больших s (например, s>8) другие генераторы наборов точек могут обеспечить гораздо меньшие расхождения.
последовательность Ван дер Корпута
[ редактировать ]Позволять
быть b -арным представлением натурального числа n ≥ 1, т.е. 0 ≤ d k ( n ) < b . Набор
Тогда существует константа C, зависящая только от b, такая, что ( g b ( n )) n ≥ 1 удовлетворяет условию
где Д * N - это звездное несоответствие .
Последовательность Холтона
[ редактировать ]
Последовательность Холтона является естественным обобщением последовательности Ван дер Корпута на более высокие измерения. Пусть s — произвольная размерность, а b 1 , ..., b s — произвольные взаимно простые целые числа, большие 1. Определим
Тогда существует константа C, зависящая только от b 1 , ..., b s , такая, что последовательность { x ( n )} n ≥1 является s -мерной последовательностью с
Набор Хаммерсли
[ редактировать ]
Пусть b 1 ,..., b s −1 — взаимно простые большие 1. Для заданных s и N s -мерное положительные целые числа , множество Хаммерсли размера N определяется формулой [7]
для n = 1, ..., N . Затем
где C — константа, зависящая только от b 1 , ..., b s −1 . Примечание. Формулы показывают, что множество Хаммерсли на самом деле является последовательностью Холтона, но мы получаем еще одно измерение бесплатно, добавляя линейную прогонку. Это возможно только в том случае, если N известно заранее. Линейный набор также является набором с наименьшей возможной одномерной невязкой в целом. К сожалению, для более высоких размерностей такие «наборы записей несоответствий» неизвестны. Для s = 2 большинство генераторов наборов точек с низким расхождением обеспечивают по крайней мере почти оптимальные расхождения.
Последовательность Соболь
[ редактировать ]Вариант Антонова-Салеева последовательности Соболя генерирует числа от нуля до единицы непосредственно как двоичные дроби длины. , из набора специальные бинарные дроби, называются номерами направлений. Биты Грея кода , , используются для выбора номеров направлений. Чтобы получить значение последовательности Соболя возьмите исключительное или двоичное значение кода Грея с соответствующим номером направления. Количество требуемых размеров влияет на выбор .
Выборка диска Пуассона
[ редактировать ]Выборка диска Пуассона популярна в видеоиграх для быстрого размещения объектов так, чтобы они выглядели случайными. но гарантирует, что каждые две точки разделены как минимум указанным минимальным расстоянием. [8] Это не гарантирует низкое расхождение (как, например, у Соболь), но, по крайней мере, значительно меньшее расхождение, чем чисто случайная выборка. Целью этих шаблонов выборки является частотный анализ, а не несоответствие, тип так называемого «синего шума».
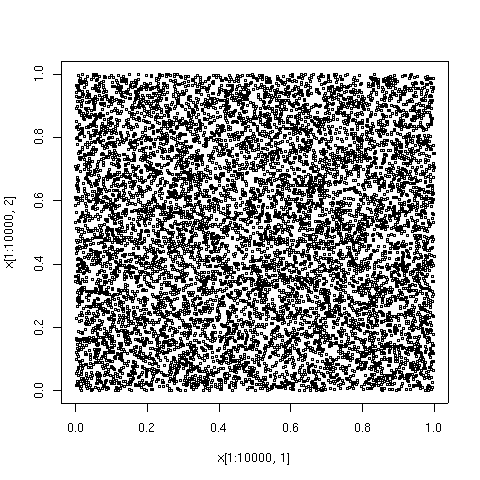
Графические примеры
[ редактировать ]Точки, нанесенные ниже, представляют собой первые 100, 1000 и 10000 элементов последовательности типа Соболь. Для сравнения также показаны 10000 элементов последовательности псевдослучайных точек. Последовательность с низким расхождением была сгенерирована алгоритмом TOMS 659. [9] Реализация алгоритма на Фортране доступна на Netlib .
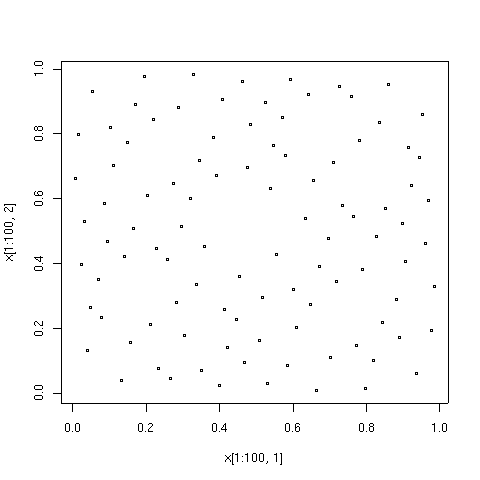
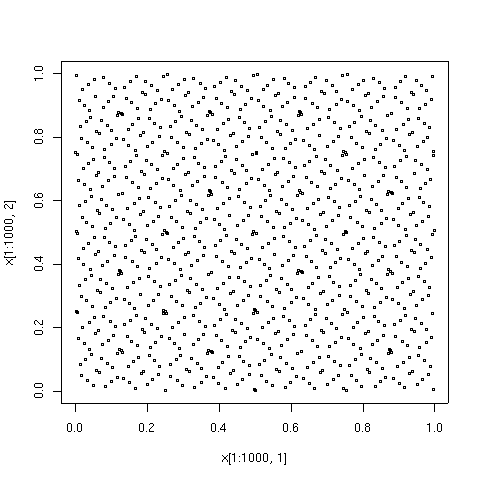
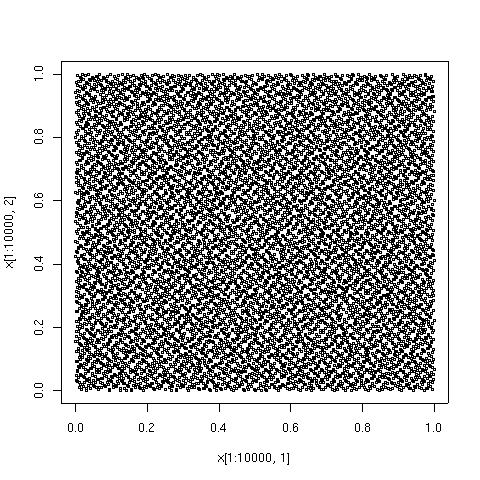
См. также
[ редактировать ]- Теория несоответствия
- Цепь Маркова Монте-Карло
- Метод квази-Монте-Карло
- Разреженная сетка
- Систематический отбор проб
Примечания
[ редактировать ]- ^ Бек, Джозеф (1989). «Двумерная теорема Ван Аарденна-Эренфеста о неоднородностях распределения » Математическая композиция . 72 (3): 269–339. МР 1032337 . S2CID 125940424 . Збл 0691.10041 .
- ^ Билык, Дмитрий; Лейси, Майкл Т.; Вагаршакян, Армен (2008). «О неравенстве малого мяча во всех измерениях» . Журнал функционального анализа . 254 (9): 2470–2502. arXiv : 0705.4619 . дои : 10.1016/j.jfa.2007.09.010 . S2CID 14234006 .
- ^ Kuipers & Niederreiter 2005 , с. 123
- ^ Кнут, Дональд Э. «Глава 3 – Случайные числа». Искусство компьютерного программирования . Том. 2.
- ^
Скарупке, Мальта (16 июня 2018 г.). «Хеширование Фибоначчи: оптимизация, о которой мир забыл» .
Одним из свойств золотого сечения является то, что вы можете использовать его для примерно равномерного разделения любого диапазона... если вы заранее не знаете, сколько шагов вы собираетесь сделать.
- ^ Робертс, Мартин (2018). «Необоснованная эффективность квазислучайных последовательностей» .
- ^ Хаммерсли, Дж. М.; Хэндскомб, округ Колумбия (1964). Методы Монте-Карло . дои : 10.1007/978-94-009-5819-7 . ISBN 978-94-009-5821-0 .
- ^ Герман Туллекен. Туллекен, Герман (март 2008 г.). «Выборка по диску Пуассона» . Дев.Маг . № 21. С. 21–25.
- ^ Братли, Пол; Фокс, Беннетт Л. (1988). «Алгоритм 659» . Транзакции ACM в математическом программном обеспечении . 14 : 88–100. дои : 10.1145/42288.214372 . S2CID 17325779 .
Ссылки
[ редактировать ]- Дик, Йозеф; Пиллихшаммер, Фридрих (2010). Цифровые сети и последовательности: теория несоответствия и интеграция квазимонте-карло . ISBN 978-0-521-19159-3 .
- Койперс, Л.; Нидеррайтер, Х. (2005), Равномерное распределение последовательностей , Dover Publications , ISBN 0-486-45019-8
- Харальд Нидеррайтер (1992). Генерация случайных чисел и методы квази-Монте-Карло . Общество промышленной и прикладной математики. ISBN 0-89871-295-5 .
- Дрмота, Майкл; Тичи, Роберт Ф. (1997). Последовательности, расхождения и приложения . Конспект лекций по математике. Том. 1651. Спрингер. ISBN 3-540-62606-9 .
- Пресс, Уильям Х.; Фланнери, Брайан П.; Теукольский, Саул А.; Веттерлинг, Уильям Т. (1992). Численные рецепты на языке C (2-е изд.). Издательство Кембриджского университета. см. раздел 7.7 для менее технического обсуждения последовательностей с низким расхождением. ISBN 0-521-43108-5 .
Внешние ссылки
[ редактировать ]- Сборник алгоритмов АКМ (см. алгоритмы 647, 659 и 738.)
- Квазислучайные последовательности из научной библиотеки GNU
- Квазислучайная выборка с учетом ограничений на FinancialMathematics.Com
- C++-генератор последовательности Соболя
- Ссылка на API SciPy QMC: scipy.stats.qmc














![{\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}f(x_{i})-\int _{{\bar {I}}^{s}}f (u)\,du=\sum _{\emptyset \neq u\subseteq D}(-1)^{|u|}\int _{[0,1]^{|u|}}\operatorname {disc } (x_{u},1){\frac {\partial ^{|u|}}{\partial x_{u}}}f(x_{u},1)\,dx_{u},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/646d05c4c12cae58e128651816856d90c9a25e51)



![{\displaystyle \operatorname {disc} _{d}(\{t_{i}\})=\left(\sum _{\emptyset \neq u\subseteq D}\int _{[0,1]^{ |u|}}\operatorname {диск} (x_{u},1)^{2}\,dx_{u}\right)^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609a886b91fa44773d2ddd89c752bc1a037309a6)
![{\displaystyle \|f\|_{d}=\left(\sum _{u\subseteq D}\int _{[0,1]^{|u|}}\left|{\frac {\partial ^{|u|}}{\partial x_{u}}}f(x_{u},1)\right|^{2}dx_{u}\right)^{1/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee8232a0985af6392e00e77e9bdfa8c4f98fe77)








































