Уравнение Ван Деемтера
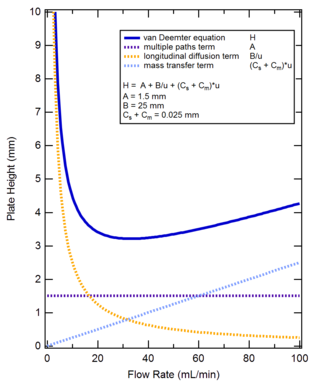
Уравнение Ван Деемтера в хроматографии , названное в честь Яна ван Деемтера , связывает дисперсию на единицу длины разделительной колонны с линейной подвижной фазы скоростью , учитывая физические, кинетические и термодинамические свойства разделения. [1] Эти свойства включают пути внутри колонны, диффузию ( осевую и продольную) и массопереноса кинетику между неподвижной и подвижной фазами. В жидкостной хроматографии скорость подвижной фазы принимается за скорость на выходе, то есть отношение скорости потока в мл/секунду к площади поперечного сечения «пути потока на выходе из колонки». Для насадочной колонны площадь поперечного сечения выходного тракта колонны обычно принимается равной 0,6 площади поперечного сечения колонны. Альтернативно линейную скорость можно принять как отношение длины колонны к мертвому времени. Если подвижной фазой является газ, то по давлению необходимо применить поправку . Дисперсия на единицу длины колонны принимается как отношение длины колонны к эффективности колонны в теоретических тарелках . Уравнение Ван Деемтера представляет собой гиперболическую функцию , которая предсказывает, что существует оптимальная скорость, при которой будет минимальная дисперсия на единицу длины столбца и, следовательно, максимальная эффективность. Уравнение Ван Деемтера было результатом первого применения теории скорости к процессу хроматографического элюирования.
Уравнение Ван Деемтера
[ редактировать ]Уравнение Ван Деемтера связывает высоту, эквивалентную теоретической тарелке (HETP) хроматографической колонки, с различными параметрами потока и кинетикой, которые вызывают уширение пика, а именно:
Где
- HETP = мера разрешающей способности колонки [м]
- A = параметр вихревой диффузии , связанный с каналированием через неидеальную насадку [м]
- B = коэффициент диффузии элюирующих частиц в продольном направлении, приводящий к дисперсии [м 2 с −1 ]
- C = сопротивление коэффициенту массопереноса аналита между подвижной и неподвижной фазой [с]
- u = скорость [мс −1 ]
В открытых трубчатых капиллярах член А будет равен нулю, поскольку отсутствие упаковки означает, что каналообразование не происходит. Однако в упакованных столбцах через упаковку столбцов существует несколько различных маршрутов («каналов»), что приводит к расширению полос. В последнем случае А не будет равно нулю.
Форма уравнения Ван Деемтера такова, что HETP достигает минимального значения при определенной скорости потока. При такой скорости потока разрешающая способность колонки максимальна, хотя на практике время элюирования, скорее всего, будет нецелесообразным. Дифференцируя уравнение Ван Деемтера по скорости, приравнивая полученное выражение к нулю и находя оптимальную скорость, получаем следующее:
Количество тарелок
[ редактировать ]
Высота пластины определяется как:
с длина столбца и количество теоретических тарелок можно оценить по хроматограмме путем анализа времени удерживания . для каждого компонента и его стандартного отклонения в качестве меры ширины пика при условии, что кривая элюирования представляет собой кривую Гаусса .
В этом случае количество тарелок определяется по формуле: [2]
Используя более практичную ширину пика на половине высоты уравнение:
или с шириной у основания вершины:
Расширено из Димтера
[ редактировать ]Уравнение Ван Деемтера можно расширить до: [3]
Где:
- H — высота тарелки
- λ — форма частицы (с учетом упаковки)
- d p — диаметр частиц
- γ, ω и R — константы
- D m – коэффициент диффузии подвижной фазы
- d c – диаметр капилляра
- d f – толщина пленки
- D s – коэффициент диффузии неподвижной фазы.
- u - линейная скорость
Уравнение Родригеса
[ редактировать ]Уравнение Родригеса , названное в честь Алирио Родригеса , является расширением уравнения Ван Деемтера, используемого для описания эффективности слоя проницаемых (крупнопористых) частиц. [4]
Уравнение:
где
и — внутричастное число Пекле .
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ ван Деемтер Дж. Дж., Зюйдервег Ф. Дж. и Клинкенберг А. (1956). «Продольная диффузия и сопротивление массопереносу как причины неидеальности в хроматографии». хим. англ. наук. 5 (6): 271–289. Бибкод : 1956ЧЭнС...5..271В . дои : 10.1016/0009-2509(56)80003-1 .
- ^ ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Номерной знак N ». два : 10.1351/goldbook.P04694
- ^ Казакевич Юрий. «Теория расширения зон (уравнение Ван Деемтера)» . Университет Сетон Холл . Проверено 5 февраля 2014 г.
- ^ Алирио Э. Родригес (10 октября 1997 г.). «Проницаемые упаковки и перфузионная хроматография при разделении белков». Журнал хроматографии Б. 699 (1–2): 47–61. дои : 10.1016/S0378-4347(97)00197-7 . ПМИД 9392367 .













![{\displaystyle f(\lambda)={\frac {3}{\lambda }}\left[{\frac {1}{\tanh(\lambda)}} - {\frac {1}{\lambda }} \верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5beb8548a472afdc6f139e90cbe8344efa341704)
