Теорема Долда – Тома

В алгебраической топологии теорема Дольда-Тома утверждает, что гомотопические группы бесконечного симметричного произведения связного комплекса CW такие же, как и его приведенные группы гомологий. Наиболее распространенная версия его доказательства состоит в том, чтобы показать, что композиция функторов гомотопической группы с бесконечным симметричным произведением определяет приведенную теорию гомологии. Одним из основных инструментов, используемых при этом, являются квазирасслоения . Теорема была обобщена различными способами, например, теоремой об изоморфизме Альмгрена .

Существует несколько других теорем, устанавливающих отношения между гомотопией и гомологиями, например теорема Гуревича . Другой подход даёт стабильная теория гомотопий . Благодаря теореме Фрейденталя о подвеске можно видеть, что последняя фактически определяет теорию гомологии. Тем не менее ни один из них не позволяет напрямую свести гомологию к гомотопии. Это преимущество теоремы Долда-Тома делает ее особенно интересной для алгебраической геометрии .

Теорема

Теорема Долда-Тома. Для связного комплекса CW X имеем π _n SP( X ) ≅ H̃ _n ( X ), где H̃ _n обозначает приведенные гомологии, а SP обозначает бесконечное симметрическое произведение.

Также очень полезно, что существует изоморфизм φ : π _n SP( X ) → H̃ _n ( X ), который совместим с гомоморфизмом Гуревича h : π _n ( X ) → H̃ _n ( X ), что означает, что существует коммутативная диаграмма

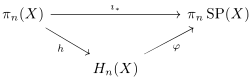
где i _* — отображение, индуцированное включением i : X = SP ¹( Икс ) → СП( Икс ).

Следующий пример показывает, что требование, чтобы X был комплексом CW, нельзя сразу отбросить:Пусть X = CH гавайской ∨ CH — клиновая сумма двух копий конуса над серьгой . Предполагается, что общей точкой двух копий является точка 0 ∈ H, пересекающая каждую окружность. С одной стороны, H ₁ ( X ) — бесконечная группа ^[1] в то время как 1 ₍ CH ) H тривиально. С другой стороны, π ₁ (SP( X )) ≅ π ₁ (SP( CH ) ) × π ₍ SP( CH Y )) имеет место, поскольку φ : SP( X ) × SP( 1 ) → SP( X ∨ Y ), определяемый формулой φ([ x ₁ , ..., x _n ], [ y ₁ , ..., y _n ]) = ([ x ₁ , ..., x _n , y ₁ , ... , y _n ]) — гомеоморфизм компактных X и Y .

Но это означает, что либо π ₁ (SP( CH ) ) ≅ H ₁ ( CH ) , либо π ₁ (SP( X )) ≅ H ₁ ( X ) не выполняется.

Эскиз доказательства

Хотим показать, что семейство функторов h _n = π _n ∘ SP определяет теорию гомологии . Дольд и Том выбрали в своем первоначальном доказательстве небольшую модификацию аксиом Эйленберга-Стинрода , а именно назвав семейство функторов ( h̃ _n ) _{n ∈ N ₀} из категории связных комплексов CW с базовой точкой в категорию абелевых групп приведенной гомологией. теории, если они удовлетворяют

Если f ≃ g : X → Y , то f _* = g _* : h̃ _n ( X ) → h̃ _n ( Y ), где ≃ обозначает точечную гомотопическую эквивалентность .
Существуют естественные граничные гомоморфизмы ∂ : h̃ _n ( X / A ) → h̃ _{n −1} ( A ) для каждой пары ( X , A ), где X и A соединены, что дает точную последовательность
$\qquad \dots \xrightarrow {\partial } {\tilde {h}}_{n}(A)\xrightarrow {i_{*}} {\tilde {h}}_{n}(X)\xrightarrow {q_{*}} {\tilde {h}}_{n}(X/A)\xrightarrow {\partial } {\tilde {h}}_{n-1}(A)\xrightarrow {i_{*}} \dots$
где i : A → X — включение, а q : X → X / A — фактор-отображение.
h̃ _n ( S ¹) = 0 при n ≠ 1, где S ¹ обозначает круг.
Пусть ( X _λ ) — система компактных подпространств точечного пространства X, содержащая базовую точку. Тогда ( X _λ ) — прямая система вместе с включениями. Обозначим через $i_{\lambda }\colon X_{\lambda }\to X$ соответственно $i_{\lambda }^{\mu }\colon X_{\lambda }\to X_{\mu }$ включение, если X _λ ⊂ X _µ . h̃ _n ( X _λ ) также является прямой системой с морфизмами ${i_{\lambda }^{\mu }}_{*}$ . Тогда гомоморфизм
$\qquad i_{*}\colon \varinjlim {\tilde {h}}_{n}(X_{\lambda })\to {\tilde {h}}_{n}(X),$
вызванный $i_{\lambda *}$ должен быть изоморфизмом.

Можно показать, что для приведенной теории гомологии ( h̃ _n ) _{n ∈ N ₀} существует естественный изоморфизм h̃ _n ( X ) ≅ H̃ _n ( X ; G ) с G = h̃ ₁ ( S ¹). ^[2]

Ясно, что h _n — функтор, обладающий свойством 1, поскольку SP — гомотопический функтор. Более того, третье свойство очевидно, поскольку SP( S ¹) ≃ С ¹. Так что остается только проверить аксиомы 2 и 4. Сутью этой затеи будет первый пункт. Здесь в игру вступают квазирасслоения :

Цель состоит в том, чтобы доказать, что отображение p _* : SP( X ) → SP( X / A ), индуцированное фактор-отображением p : X → X / A, является квазирасслоением для пары CW ( X , A ), состоящей из связных комплексов. . Прежде всего, поскольку каждый комплекс CW гомотопически эквивалентен симплициальному комплексу, ^[3] X и A можно считать симплициальными комплексами . При этом X будет заменен цилиндром отображения включения A → X . Это ничего не изменит, поскольку SP — гомотопический функтор. Достаточно по индукции доказать, что * _: En → _p B n _— квазирасслоение такое, что B _n = SP ^н( X / A ) и E _n = p _*⁻¹( Б _н ). При n = 0 это выполняется тривиально. На этапе индукции B _n разлагается на открытую окрестность B _{n −1} и B _n − B _{n −1} и показывается, что эти два множества вместе с их пересечением различимы, т. е. что p ограничено каждым из прообразов. из этих трех множеств является квазирасслоением. Можно показать, что тогда B _n уже отличится. Следовательно, p _* действительно является квазирасслоением на всем SP( X ), и из длинной точной последовательности такого квазирасслоения следует, что аксиома 2 выполняется при p _*⁻¹([e]) ≅ SP( A ).

Можно задаться вопросом, не является ли p _* даже расслоением. Однако оказывается, что это не так: возьмите произвольный путь x _t для t ∈ [0, 1) в X − A , приближающийся к некоторому a ∈ A , и интерпретируйте его как путь в X / A ⊂ SP( X / A ). любой подъем этого пути до SP( X имеет вид xtαt _, Тогда _для где αt _∈ A ) каждого t . Но это означает, что его конечная точка a α ₁ кратна a и, следовательно, отличается от базовой точки, поэтому свойство гомотопического подъема не может быть выполнено.

Проверка четвертой аксиомы может быть произведена достаточно элементарно, в отличие от предыдущей.

Следует иметь в виду, что существует множество различных доказательств, хотя это, по-видимому, самое популярное. Например, доказательства были установлены с помощью факторизации гомологии или симплициальных множеств . Можно также доказать теорему, используя другие понятия теории гомологии (например, аксиомы Эйленберга-Стинрода).

Совместимость с гомоморфизмом Гуревича.

Чтобы проверить совместимость с гомоморфизмом Гуревича, достаточно показать, что утверждение справедливо для X = S ^н. Это потому, что тогда получается призма

для каждого элемента [ f ] ∈ π _n ( X ), представленного картой f : S ^н → Х. На этой диаграмме все стороны, кроме, возможно, нижней, коммутируют. Следовательно, видно, что вся диаграмма коммутирует, если рассмотреть, где 1 ∈ π _n ( S ^н) ≅ Z отображается. Однако при использовании изоморфизмов надстройки для гомотопических групп гомологий задача сводится к доказательству утверждения для S ¹. Но в этом случае включение SP ¹( С ¹) → SP( S ¹) является гомотопической эквивалентностью.

Приложения

Последовательность Майера-Виеториса

Одним из прямых следствий теоремы Дольда-Тома является новый способ вывода последовательности Майера-Виеториса . Результат получается, если сначала сформировать квадрат гомотопического выталкивания включений пересечения A ∩ B двух подпространств A , B ⊂ X в A и B. сами Затем к этому квадрату применяется SP и, наконец, π _* к полученному квадрату отката. ^[4]

Теорема Мура

Другое применение — новое доказательство теоремы, впервые сформулированной Муром. В основном это предписывает следующее:

Теорема. Линейно-связное, коммутативное и ассоциативное H-пространство X со строгой единицей имеет слабый гомотопический тип обобщенного пространства Эйленберга-Маклейна .

Обратите внимание, что SP( Y ) обладает этим свойством для каждого связного комплекса CW Y и, следовательно, имеет слабый гомотопический тип обобщенного пространства Эйленберга-Маклейна. Теорема сводится к тому, что все k -инварианты линейно связного, коммутативного и ассоциативного H-пространства со строгой единицей равны нулю.

Доказательство

Пусть Gn _X = _πn ( ) . Тогда существуют отображения M ( Gn _, ( n → X, изоморфизм на πn _, если n ≥ 2, и изоморфизм на H1 _, если n = 1 для пространства Мура M ) Gn _{индуцирующие} , n ). ^[5] Они дают карту

\bigvee _{n}M(G_{n},n)\to X

если считать, что карты сохраняют базовую точку. Тогда специальная структура H-пространства X дает отображение

f\colon \operatorname {SP} \left(\bigvee _{n}M(G_{n},n)\right)\to X

дается суммированием изображений координат. Но поскольку существуют естественные гомеоморфизмы

\operatorname {SP} \left(\bigvee _{\alpha }X_{\alpha }\right)\cong \prod _{\alpha }\operatorname {SP} (X_{\alpha }),

где Π обозначает слабое произведение, f индуцирует изоморфизмы на π _n для n ≥ 2. Но при π ₁ ( X ) → π ₁ SP( X ) = H ₁ ( X ), индуцированном включением X → SP( X ), является Гомоморфизм Гуревича, а поскольку H-пространства имеют абелевы фундаментальные группы, f также индуцирует изоморфизмы на π ₁ . Благодаря теореме Долда-Тома каждый SP( ) ) теперь _{является} M(Gn, пространством Эйленберга-Маклейна K ( Gn _n , n ). Отсюда также следует, что естественное включение слабого произведения Π _n SP( M ( G _n , n )) в декартово произведение является слабой гомотопической эквивалентностью. Следовательно, X имеет слабый гомотопический тип обобщенного пространства Эйленберга-Маклейна.

Алгебраическая геометрия

Что отличает теорему Долда-Тома от других альтернативных оснований гомологии, таких как когомологии Чеха или Александера-Спанье, так это то, что она представляет особый интерес для алгебраической геометрии, поскольку позволяет переформулировать гомологии только с использованием гомотопии. Поскольку применение методов алгебраической топологии может быть весьма полезным в этой области, их пытаются перенести в алгебраическую геометрию. Этого можно было достичь для теории гомотопий, но для теории гомологии лишь весьма ограниченным образом, используя формулировку через пучки . Таким образом, теорема Дольда-Тома дает основу гомологии, имеющую алгебраический аналог. ^[6]

Примечания

^ Дольд и Том (1958), Пример 6.11.
^ Дольд и Том (1958), Теорема 6.8
^ Хэтчер (2002), Теорема 2C.5
^ Теорема Долда-Тома о nLab
^ Хэтчер (2002), Лемма 4.31.
^ Теорема Долда-Тома. Эссе Томаса Барнета-Лэмба.

Ссылки

Агилар, Марсело; Гитлер, Самуэль; Прието, Карлос (2008). Алгебраическая топология с гомотопической точки зрения . Springer Science & Business Media. ISBN 978-0-387-22489-3 .
Бандклайдер, Лорен (2019), «Теорема Долда-Тома через факториационную гомологию», Журнал гомотопии и связанных источников , 14 (2): 579–593, doi : 10.1007/s40062-018-0219-1 , S2CID 256333418
Дольд, Альбрехт; Том, Рене (1958), «Квазирасслоения и бесконечные симметричные произведения», Annals of Mathematics , Second Series, 67 (2): 239–281, doi : 10.2307/1970005 , ISSN 0003-486X , JSTOR 1970005 , MR 0097062
Хэтчер, Аллен (2002). Алгебраическая топология . Издательство Кембриджского университета . ISBN 978-0-521-79540-1 .
Мэй, Дж. Питер (1990), «Слабые эквивалентности и квазирасслоения», Конспекты лекций Springer , Конспекты лекций по математике, 1425 : 91–101, doi : 10.1007/BFb0083834 , ISBN 978-3-540-52658-2
Пиччинини, Ренцо А. (1992). Лекции по теории гомотопии . Эльзевир. ISBN 9780080872827 .
Спанье, Эдвин (1959), «Бесконечные симметричные произведения, функциональные пространства и двойственность», Annals of Mathematics : 142–198, doi : 10.2307/1970099 , JSTOR 1970099

Внешние ссылки

[1] Дольд и Том (1958), Пример 6.11.

[2] Дольд и Том (1958), Теорема 6.8

[3] Хэтчер (2002), Теорема 2C.5

[4] Теорема Долда-Тома о nLab

[5] Хэтчер (2002), Лемма 4.31.

[6] Теорема Долда-Тома. Эссе Томаса Барнета-Лэмба.

[1]

[2]

[3]

[4]

[5]

[6]