Боковое давление грунта

Пример бокового давления грунта, опрокидывающего подпорную стену

Боковое давление грунта – это давление , которое грунт оказывает в горизонтальном направлении. Это важно, поскольку оно влияет на характеристики консолидации и прочность грунта, а также потому, что оно учитывается при проектировании инженерно-геологических сооружений, таких как подпорные стены , подвалы , туннели , глубокие фундаменты и раскопки.

Проблема давления земли возникла в начале 18 века, когда Готье перечислил пять областей, требующих исследования, одной из которых были размеры гравитационных подпорных стен, необходимых для удержания почвы. Однако первый крупный вклад в область давления Земли был сделан несколько десятилетий спустя Кулоном. который рассматривал твердую массу почвы, скользящую по поверхности сдвига. Рэнкин расширенная теория давления грунта путем получения решения для всего массива грунта в состоянии разрушения по сравнению с решением Кулона, которое рассматривало массив грунта, ограниченный единственной поверхностью разрушения. Первоначально теория Рэнкина рассматривала случай только несвязных грунтов, причем Белл впоследствии расширив его, чтобы охватить случай грунтов, обладающих как сцеплением, так и трением. Како и Керисель модифицированные уравнения Мюллера-Бреслау для учета неплоской поверхности разрыва.

Коэффициент бокового давления грунта

Коэффициент бокового давления грунта K определяется как отношение горизонтального эффективного напряжения σ' _h к вертикальному эффективному напряжению σ' _v . Эффективное напряжение — это межзеренное напряжение, рассчитанное путем вычитания порового давления воды из общего напряжения, как описано в механике грунтов . K для конкретного почвенного отложения является функцией свойств почвы и истории напряжений. Минимальное стабильное значение K называется коэффициентом активного давления грунта K _a ; активное давление грунта получается, например, при удалении подпорной стенки от грунта. Максимальное стабильное значение K называется коэффициентом пассивного давления грунта K _p ; пассивное давление грунта будет развиваться, например, против вертикального плуга, который толкает почву горизонтально. Для ровного грунта с нулевой боковой деформацией в почве _{коэффициент бокового давления грунта «в состоянии покоя» K 0} получен .

Существует множество теорий прогнозирования бокового давления земли; некоторые из них основаны эмпирически , а некоторые получены аналитическим путем.

Определения символов

В этой статье следующие переменные в уравнениях определяются следующим образом:

оптическое распознавание символов

Коэффициент сверхконсолидации

б

Угол обратного откоса, измеренный к горизонту

д

Угол трения стены

я

Угол стены, измеренный к вертикали

ж

Угол трения напряжения в почве

е'

Эффективный угол трения напряжения грунта

φ' _cs

Эффективный угол трения напряжения грунта в критическом состоянии

В состоянии покоя давление

Боковое давление грунта на месте называется давлением грунта в состоянии покоя и обычно рассчитывается как произведение напряжения вскрышных пород на коэффициент K ₀ ; последний называется коэффициентом давления грунта в состоянии покоя. K ₀ может быть получен непосредственно в полевых условиях, например, с помощью дилатометрического испытания (DMT) или скважинного прессиометрического испытания (PMT), хотя его чаще рассчитывают с использованием хорошо известной формулы Джаки. Для рыхлоотложенных песков в состоянии покоя Джаки аналитически показал, что K ₀ отклоняется от единицы с тенденцией к снижению по мере увеличения синусоидального члена угла внутреннего трения материала, т.е.

$K_{0(NC)}=1-\sin \phi '$

Позже было доказано, что коэффициент Джаки справедлив и для нормально консолидированных зернистых отложений. и нормально консолидированные глины.

С чисто теоретической точки зрения очень простой $1-\sin \phi '$ формула идеально работает для двух крайних значений $\phi '$, где для $\phi '$ = 0 ^тот это дает $K_{0}=1$ ссылаясь на гидростатические условия и для $\phi '$ = 90 ^тот (теоретическое значение) это дает $K_{0}=0$ относится к фрикционному материалу, который может стоять вертикально без поддержки, не оказывая таким образом бокового давления. Эти крайние случаи являются достаточным доказательством того, что правильным выражением для коэффициента давления грунта в состоянии покоя является $K_{0}=1-\sin \phi '$.

Существует общее впечатление, что коэффициент давления грунта в состоянии покоя, предложенный Джаки (1944), является эмпирическим и, действительно, $K_{0}=1-\sin \phi '$ выражение является просто упрощением выражения ниже:

$K_{0(NC)}={\frac {1+2/3\sin \phi '}{1+\sin \phi '}}(1-\sin \phi ')$

Однако последнее происходит в результате полностью аналитической процедуры и соответствует промежуточному состоянию между состоянием покоя и активным состоянием (дополнительную информацию см. в Пантелидисе). ).

Как упоминалось ранее, согласно литературе, Джеки $K_{0}=1-\sin \phi '$ уравнение очень хорошо соответствует экспериментальным данным как для нормально консолидированных песков, так и для глин. Однако некоторые исследователи утверждают, что слегка измененные формы уравнения Джеки лучше соответствуют их данным. Однако, хотя некоторые из этих модификаций приобрели большую популярность, они не дают лучших оценок $K_{0}$. Например, Брукер и Айрлендс $K_{0}=0.95-\sin \phi '$ основано на лабораторном определении $K_{0}$ только пяти образцов, тогда как эффективный угол сопротивления сдвигу трех из них был получен из литературы, не имея никакого контроля над ними. Более того, уточнения порядка нескольких процентных пунктов скорее подтверждают обоснованность $K_{0}=1-\sin \phi '$ выражения, чем превосходство утонченного выражения.

Для переуплотненных почв Mayne & Kulhawy предложил следующее выражение:

$K_{0(OC)}=K_{0(NC)}*OCR^{(\sin \phi ')}\$

Последнее требует профиля OCR определения с глубиной. OCR – это коэффициент сверхконсолидации и $\phi '$ – эффективный угол трения напряжения.

Чтобы оценить K ₀ из-за давления уплотнения , обратитесь к Ingold (1979).

Пантелидис предложил аналитическое выражение для коэффициента давления грунта в состоянии покоя, применимое к связно-фрикционным грунтам и как горизонтальным, так и вертикальным псевдостатическим условиям, что является частью единого подхода механики сплошных сред (рассматриваемое выражение приведено в разделе ниже) .

Боковое активное давление и пассивное сопротивление почвы

Различные типы стеновых конструкций могут быть спроектированы так, чтобы противостоять давлению грунта.

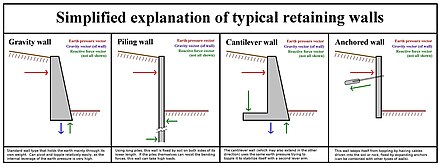
Активное состояние возникает, когда удерживаемой массе почвы позволяют расслабиться или деформироваться вбок и наружу (от массы почвы) до такой степени, что она мобилизует все свое доступное сопротивление сдвигу (или задействует свою прочность на сдвиг) в попытке противостоять боковой деформации. То есть почва находится в точке начального разрушения в результате сдвига из-за разгрузки в боковом направлении. Это минимальное теоретическое боковое давление, которое данная масса грунта будет оказывать на подпорную стенку, которая будет перемещаться или вращаться в направлении от грунта до тех пор, пока не будет достигнуто активное состояние грунта (не обязательно фактическое боковое давление в процессе эксплуатации на стены, которые не двигаются). при воздействии бокового давления почвы, превышающего активное давление).

Пассивное состояние возникает, когда масса почвы подвергается внешнему давлению вбок и внутрь (по направлению к массе почвы) до такой степени, что мобилизует свое полное сопротивление сдвигу в попытке противостоять дальнейшей боковой деформации. То есть масса грунта находится в точке начального разрушения в результате сдвига из-за нагрузки в боковом направлении. Это максимальное боковое сопротивление, которое данный массив грунта может оказать подпорной стенке, прижимаемой к массиву грунта. То есть почва находится на начальном этапе разрушения в результате сдвига, но на этот раз из-за нагрузки в боковом направлении. Таким образом, активное давление и пассивное сопротивление определяют минимальное боковое давление и максимальное боковое сопротивление, возможное для данной массы почвы.

Коэффициенты давления Земли Кулона

Кулон (1776 г.) впервые изучил проблему бокового давления грунта на подпорные конструкции. Он использовал теорию предельного равновесия, которая рассматривает разрушающийся блок грунта как свободное тело , чтобы определить предельное горизонтальное давление грунта.

Предельное горизонтальное давление при разрушении при растяжении или сжатии используется для определения $K_{a}$ и $K_{p}$ соответственно. Поскольку проблема неопределенная , необходимо проанализировать ряд потенциальных поверхностей разрушения, чтобы определить критическую поверхность разрушения (т. е. поверхность, которая создает максимальную или минимальную нагрузку на стену). Основное предположение Кулона состоит в том, что поверхность разрушения плоская.

Мейньел (1808) позже расширил уравнения Кулона, чтобы учесть трение стенок, обозначенное $\delta$. Мюллер-Бреслау (1906) дальнейшее обобщение уравнений Мейнеля для негоризонтальной засыпки и невертикальной границы раздела грунт-стена (представленной углом $\theta$ от вертикали).

$K_{a}={\frac {\cos ^{2}\left(\phi '-\theta \right)}{\cos ^{2}\theta \cos \left(\delta +\theta \right)\left(1+{\sqrt {\frac {\sin \left(\delta +\phi '\right)\sin \left(\phi '-\beta \right)}{\cos \left(\delta +\theta \right)\cos \left(\beta -\theta \right)}}}\ \right)^{2}}}$

$K_{p}={\frac {\cos ^{2}\left(\phi '+\theta \right)}{\cos ^{2}\theta \cos \left(\delta -\theta \right)\left(1-{\sqrt {\frac {\sin \left(\delta +\phi '\right)\sin \left(\phi '+\beta \right)}{\cos \left(\delta -\theta \right)\cos \left(\beta -\theta \right)}}}\ \right)^{2}}}$

Вместо вычисления приведенных выше уравнений или использования для этого коммерческих программных приложений можно использовать сборники таблиц для наиболее распространенных случаев. Обычно вместо $K_{a}$, горизонтальная часть $K_{ah}$ сведено в таблицу. Это то же самое, что $K_{a}$ раз $\cos(\delta +\theta )$. [Обратите внимание, что при определенных условиях уравнение для $K_{p}$ «взрывается». Например, если $\theta =\beta =0$ и $\phi '=\delta =45^{\circ }$, затем $K_{p}\to \infty$.]

Фактическая сила давления земли $E_{a}$ это сумма части $E_{ag}$ из-за веса земли часть $E_{ap}$ из-за дополнительных нагрузок, таких как транспорт, минус часть $E_{ac}$ из-за наличия какой-либо сплоченности.

$E_{ag}$ – интеграл от давления по высоте стены, который равен $K_{a}$ умножить на удельный вес земли и на половину высоты стены в квадрате.

В случае равномерной сжимающей нагрузки на террасу над подпорной стеной: $E_{ap}$ соответствует этому давлению раз $K_{a}$ раза больше высоты стены. Это применимо, если терраса горизонтальна, а стена вертикальна. В противном случае, $E_{ap}$ необходимо умножить на ${\frac {\cos \theta \cdot \cos \beta }{\cos(\theta -\beta )}}$.

$E_{ac}$ обычно считается равным нулю, если только значение связности не может поддерживаться постоянно.

$E_{ag}$ действует на поверхность стены на трети ее высоты снизу и под углом $\delta$ относительно прямого угла у стены. $E_{ap}$ действует под тем же углом, но на половине высоты.

Коэффициенты давления земли Рэнкина и расширение Белла для связных грунтов

Теория Рэнкина , разработанная в 1857 году, представляет собой решение для определения поля напряжений, которое прогнозирует активное и пассивное давление грунта. Предполагается, что грунт несвязный, стена не повреждена и не подвержена трению, а засыпка горизонтальна. Поверхность разрушения, по которой движется грунт, плоская . Ниже приведены выражения для активных и пассивных коэффициентов бокового давления грунта.

$K_{a}=\tan ^{2}\left(45-{\frac {\phi '}{2}}\right)={\frac {1-\sin(\phi ')}{1+\sin(\phi ')}}$

$K_{p}=\tan ^{2}\left(45+{\frac {\phi '}{2}}\right)={\frac {1+\sin(\phi ')}{1-\sin(\phi ')}}$

Для связных почв Bell разработал аналитическое решение, которое использует квадратный корень из коэффициента давления для прогнозирования вклада сцепления в общее результирующее давление. Эти уравнения представляют общее боковое давление грунта. Первый член представляет несвязный вклад, а второй член - связный вклад. Первое уравнение относится к состоянию активного давления грунта, а второе — к состоянию пассивного давления грунта.

$\sigma _{a}=K_{a}\sigma _{v}-2c'{\sqrt {K_{a}}}\$

$\sigma _{p}=K_{p}\sigma _{v}+2c'{\sqrt {K_{p}}}\$

Обратите внимание, что c' и φ' — это эффективное сцепление и угол сопротивления грунта сдвигу соответственно. Для связных грунтов глубина трещины растяжения (относительно активного состояния) равна: $$z_{tc}={\frac {2c'}{\gamma \tan {(45^{o}-\phi '/2)}}}$$Для чисто фрикционных грунтов с наклонной засыпкой, оказывающей давление на ненарушенную, не трущуюся стену, коэффициенты составляют:

$K_{a}=\cos \beta {\frac {\cos \beta -{\sqrt {\cos ^{2}\beta -\cos ^{2}\phi '}}}{\cos \beta +{\sqrt {\cos ^{2}\beta -\cos ^{2}\phi '}}}}$

$K_{p}=\cos \beta {\frac {\cos \beta +{\sqrt {\cos ^{2}\beta -\cos ^{2}\phi '}}}{\cos \beta -{\sqrt {\cos ^{2}\beta -\cos ^{2}\phi '}}}}$

с горизонтальными составляющими давления грунта:

$\sigma _{a}=K_{a}\gamma z\cos \beta$

$\sigma _{p}=K_{p}\gamma z\cos \beta$

где β – угол наклона засыпки.

Анализ Какота и Керизеля для поверхностей разрушения в виде бревенчатой ​​спирали

В 1948 году Альберт Како (1881–1976) и Жан Керизель (1908–2005) разработал продвинутую теорию, которая модифицировала уравнения Мюллера-Бреслау для учета неплоской поверхности разрыва. Вместо этого они использовали логарифмическую спираль для изображения поверхности разрыва. Эта модификация чрезвычайно важна для пассивного давления грунта, когда существует трение грунта о стенки. Уравнения Майниеля и Мюллера-Бреслау в этой ситуации неконсервативны и их опасно применять. По коэффициенту активного давления логарифмическая спиральная поверхность разрыва обеспечивает незначительную разницу по сравнению с Мюллером-Бреслау. Эти уравнения слишком сложны для использования, поэтому вместо них используются таблицы или компьютеры.

Коэффициенты давления грунта Мононобе-Окабе и Капиллы для динамических условий.

Мононобе-Окабе и Капилла Коэффициенты давления грунта для динамических активных и пассивных условий соответственно были получены на той же основе, что и решение Кулона. Эти коэффициенты приведены ниже:

$$K_{ae}={\frac {\cos ^{2}{(\phi '-\psi -\beta )}}{\cos {\psi }\cos ^{2}{\beta }\cos(\delta +\beta +\psi ){\Bigl (}1+{\sqrt {\frac {\sin {(\phi '+\delta )}\sin {(\phi '-\psi +\alpha )}}{\sqrt {\cos {(\delta +\beta +\phi )}\cos {(\alpha -\beta )}}}}}{\Bigr )}^{2}}}$$$$K_{pe}={\frac {\cos ^{2}{(\phi '-\psi +\beta )}}{\cos {\psi }\cos ^{2}{\beta }\cos(\delta -\beta +\psi ){\Bigl (}1-{\sqrt {\frac {\sin {(\phi '+\delta )}\sin {(\phi '-\psi +\alpha )}}{\sqrt {\cos {(\delta -\beta +\phi )}\cos {(\alpha -\beta )}}}}}{\Bigr )}^{2}}}$$с горизонтальными составляющими давления грунта: $\sigma _{a}=K_{a}\gamma z\cos \beta$

$\sigma _{p}=K_{p}\gamma z\cos \beta$

где, ${\textstyle k_{h}}$ и ${\textstyle k_{v}}$ – сейсмические коэффициенты горизонтального и вертикального ускорения соответственно, ${\textstyle \psi =\arctan {(k_{h}/(1-k_{v}))}}$, ${\textstyle \beta }$ - угол наклона задней грани конструкции относительно вертикали, ${\textstyle \delta }$ - угол трения между конструкцией и грунтом и ${\textstyle \alpha }$ - наклон заднего склона.

Вышеуказанные коэффициенты включены в многочисленные нормы сейсмического проектирования по всему миру (например, EN1998-5, ААШТО ), поскольку Сид и Уитмен предложили его в качестве стандартных методов. Проблемы с этими двумя решениями известны (см., например, Anderson ]), причем наиболее важным из них является квадратный корень из отрицательного числа для ${\textstyle \phi '<\psi \mp \beta }$ (знак минус обозначает активный случай, а знак плюс — пассивный).

Различные нормы проектирования признают проблему с этими коэффициентами и либо пытаются интерпретировать, либо диктуют модификацию этих уравнений, либо предлагают альтернативы. В этом отношении:

• Еврокод 8 диктует (без каких-либо объяснений), что весь квадратный корень в формуле Мононобе-Окабе, если он отрицательный, должен быть произвольно заменен единицей
• ААШТО, В дополнение к проблеме с квадратным корнем, признал консервативность решения Мононобе-Окабе, приняв в качестве стандартной практики проектирования использование коэффициента уменьшения для ожидаемого пикового ускорения грунта, предполагая ${\textstyle k_{h}=(1/2)PGA}$ (где ${\textstyle PGA}$ это пиковое ускорение относительно земли)
• Совет по сейсмической безопасности зданий предполагает, что ${\textstyle k_{h}=(2/3)PGA}$ по той же причине, что и выше
• Отчет ГЕО № 45 Инженерно-геологического управления Гонконга предписывает использовать метод пробного клина, когда число под квадратным корнем отрицательно.

Отмечается, что приведенные выше эмпирические поправки на ${\textstyle k_{h}}$ сделано AASHTO и Совет по сейсмической безопасности зданий Коэффициенты возврата давления грунта очень близки к тем, которые получены с помощью аналитического решения, предложенного Пантелидисом. (см. ниже).

Подход Мазиндрани и Ганджале для связно-фрикционных грунтов с наклонной поверхностью.

Мазиндрани и Гянджале представил аналитическое решение проблемы давления грунта, оказываемого на гладкую, неразрушенную стену связно-фрикционным грунтом с наклонной поверхностью. Выведенные уравнения приведены ниже как для активного, так и для пассивного состояний:

$K_{a}={\frac {1}{\cos ^{2}\phi '}}{\biggl (}2\cos ^{2}\beta +2{\frac {c'}{\gamma z}}\cos \phi '\sin \phi '-{\sqrt {4\cos ^{2}\beta {\Bigl (}\cos ^{2}\beta -\cos ^{2}\phi '{\Bigr )}+4{\biggl (}{\frac {c'}{\gamma z}}{\biggl )}^{2}\cos ^{2}\phi '+8{\biggl (}{\frac {c'}{\gamma z}}{\biggl )}\cos ^{2}\beta \sin \phi '\cos \phi '}}{\biggl )}-1$

$K_{p}={\frac {1}{\cos ^{2}\phi '}}{\biggl (}2\cos ^{2}\beta +2{\frac {c'}{\gamma z}}\cos \phi '\sin \phi '+{\sqrt {4\cos ^{2}\beta {\Bigl (}\cos ^{2}\beta -\cos ^{2}\phi '{\Bigr )}+4{\biggl (}{\frac {c'}{\gamma z}}{\biggl )}^{2}\cos ^{2}\phi '+8{\biggl (}{\frac {c'}{\gamma z}}{\biggl )}\cos ^{2}\beta \sin \phi '\cos \phi '}}{\biggl )}-1$

с горизонтальными составляющими активного и пассивного давления грунта составляют:

$\sigma _{a}=K_{a}\gamma z\cos \beta$

$\sigma _{p}=K_{p}\gamma z\cos \beta$

коэффициенты ka и kp для различных значений ${\textstyle \phi '}$, ${\textstyle \beta }$, и ${\textstyle c'/(\gamma z)}$ в табличной форме можно найти в Мазиндрани и Гянджале.

На основе аналогичной аналитической процедуры Гнанапрагасам дал другое выражение для ка. Однако отмечается, что выражения Мазиндрани, Ганджале и Гнанапрагасама приводят к идентичным значениям активного давления земли.

При любом подходе к активному давлению грунта глубина трещины растяжения оказывается такой же, как и в случае нулевого наклона обратной засыпки (см. расширение Беллом теории Рэнкина).

Единый подход Пантелидиса: обобщенные коэффициенты давления грунта

Пантелидис предложил единый полностью аналитический подход механики сплошной среды (основанный на первом законе движения Коши) для получения коэффициентов давления грунта для всех состояний почвы, применимый к связно-фрикционным грунтам, а также к горизонтальным и вертикальным псевдостатическим условиям.

Используются следующие символы:

${\textstyle k_{h}}$ и ${\textstyle k_{v}}$ - сейсмические коэффициенты горизонтального и вертикального ускорения соответственно

${\textstyle c'}$, ${\textstyle \phi '}$ и ${\textstyle \gamma }$ — эффективное сцепление, эффективный угол внутреннего трения (максимальные значения) и удельный вес грунта соответственно.

${\textstyle c_{m}}$ – это мобилизованное сцепление грунта (мобилизованная прочность грунта на сдвиг, т.е. ${\textstyle c_{m}}$и ${\textstyle \phi _{m}}$ параметры могут быть получены аналитически или с помощью соответствующих графиков; см. Пантелидис )

${\textstyle E}$ и ${\textstyle \nu }$ — эффективные упругие константы грунта (т.е. модуль Юнга и коэффициент Пуассона соответственно)

${\textstyle H}$ высота стены

${\textstyle z}$ это глубина, на которой рассчитывается давление грунта

Коэффициент давления грунта в состоянии покоя

$$K_{oe}=(1-\sin \phi ')\left(1+{\frac {k_{h}}{1-k_{v}}}\tan \phi '\right)-{\frac {1}{1-k_{v}}}{\frac {2c_{m}}{\gamma z}}\tan \left(45^{o}-{\frac {\phi '}{2}}\right)$$с ${\textstyle \sigma _{o}=K_{oe}(1-k_{v})\gamma z}$

Коэффициент активного давления грунта

$$K_{ae}={\frac {1-\sin \phi '}{1+\sin \phi '}}\left(1+2{\frac {k_{h}}{1-k_{v}}}\tan \phi '\right)-{\frac {1}{1-k_{v}}}{\frac {2c_{m}}{\gamma z}}\tan \left(45^{o}-{\frac {\phi '}{2}}\right)$$с ${\textstyle \sigma _{a}=K_{ae}(1-k_{v})\gamma z}$

Коэффициент пассивного давления грунта

$$K_{pe}={\frac {1+\sin \phi '}{1-\sin \phi '}}\left(1-2{\frac {k_{h}}{1-k_{v}}}\tan \phi '\right)+{\frac {1}{1-k_{v}}}{\frac {2c_{m}}{\gamma z}}\tan \left(45^{o}+{\frac {\phi '}{2}}\right)$$с ${\textstyle \sigma _{p}=K_{pe}(1-k_{v})\gamma z}$

Коэффициент промежуточного давления грунта на активной «стороне»

$$K_{xe,a}={\biggl (}{\frac {1-\sin \phi '}{1+\sin \phi '}}{\biggr )}{\biggl (}\left(1-\xi \sin \phi '\right)-{\frac {k_{h}}{1-k_{v}}}\tan \phi '(2+\xi (1-\sin \phi ')){\biggl )}-{\frac {1}{1-k_{v}}}{\frac {2c_{m}}{\gamma z}}\tan \left(45^{o}-{\frac {\phi '}{2}}\right)$$с ${\textstyle \sigma _{x,a}=K_{xe,a}(1-k_{v})\gamma z}$

Коэффициент промежуточного давления грунта на пассивной «стороне»

$$K_{xe,p}={\biggl (}{\frac {1+\sin \phi '}{1-\sin \phi '}}{\biggr )}^{\xi _{1}}{\biggl (}\left(1+\xi \sin \phi '\right)+\xi _{2}{\frac {k_{h}}{1-k_{v}}}\tan \phi '(2+\xi (1+\sin \phi ')){\biggl )}+{\frac {1}{1-k_{v}}}{\frac {2c_{m}}{\gamma z}}{\Biggl (}{\frac {\tan \left(45^{o}+{\frac {\phi '}{2}}\right)}{\tan \left(45^{o}-{\frac {\phi '}{2}}\right)}}{\Biggr )}^{\xi _{1}}\tan \left(45^{o}-{\frac {\phi '}{2}}\right)$$где, ${\textstyle \xi _{1}=1+\xi }$, ${\textstyle \xi _{2}={\frac {2}{m}}-1}$, ${\textstyle \xi ={\frac {m-1}{m+1}}{\Bigl (}1-{\frac {1}{m}}{\Bigr )}-1}$ и ${\textstyle m={\Bigl (}1-{\frac {\Delta x}{\Delta x_{max}}}{\Bigr )}^{-1}}$

с ${\textstyle \sigma _{x,p}=K_{xe,p}(1-k_{v})\gamma z}$

${\textstyle \xi _{1}}$ и ${\textstyle \xi _{2}}$ – параметры, связанные с переходом от грунтового клина состояния покоя к грунтовому клину пассивного состояния (т.е. угол наклона грунтового клина, изменяющийся от ${\textstyle 45^{o}+\phi '/2}$ к ${\textstyle 45^{o}-\phi '/2}$.Также, ${\textstyle \Delta x}$ и ${\textstyle \Delta x_{max}}$ – боковое смещение стенки и боковое (максимальное) смещение стенки, соответствующее активному или пассивному состоянию (как на глубине ${\textstyle z}$). Последний приведен ниже.

Максимальное боковое смещение стены, соответствующее активному или пассивному состоянию.

$$\Delta x_{max}={\frac {\pi }{4}}{\frac {1-\nu ^{2}}{E}}{\frac {(H+z)^{3}(H-z)}{H^{2}z}}\Delta \mathrm {K} (1-k_{v})\gamma z$$для гладкой подпорной стены и $$\Delta x_{max}={\frac {\pi }{4}}{\frac {(3-\nu -4\nu ^{2})(1+\nu )}{E}}{\Biggl (}{\frac {1-\nu ^{2}}{H^{2}-z^{2}}}+{\frac {\nu (1+\nu )H-(1-\nu ^{2})z}{(H+z)^{3}}}{\Biggl )}^{-1}{\frac {1}{H}}\Delta \mathrm {K} (1-k_{v})\gamma z$$для грубой подпорной стены

с ${\textstyle \Delta \mathrm {K} =K_{oe}-K_{xe,a}}$ или ${\textstyle \Delta \mathrm {K} =K_{xe,p}-K_{oe}}$ для активной и пассивной «стороны» соответственно.

Глубина трещины растяжения (активное состояние) или нейтральной зоны (состояние покоя)

Глубина нейтральной зоны в состоянии покоя составляет: $$z_{nz}={\frac {c'}{(1-k_{v})\gamma \tan {\phi '}}}{\Biggl [}{\frac {1}{{\biggl (}\cos {\phi '}+{\frac {k_{h}}{1-k_{v}}}\sin {\phi '}{\biggl )}^{2}}}-1{\Biggl ]}$$при этом глубина трещины растяжения в активном состоянии составляет: $$z_{tc}={\frac {c'}{(1-k_{v})\gamma \tan {\phi '}}}{\Biggl [}{\frac {\tan ^{2}(45+\phi '/2)}{{\biggl (}1+2{\frac {k_{h}}{1-k_{v}}}\tan {\phi '}{\biggl )}^{2}}}-1{\Biggl ]}$$В статических условиях ( $k_{h}$= $k_{v}$=0), где мобилизованная сплоченность, $c_{m}$, равен значению сцепления в критическом состоянии, $c'$, приведенное выше выражение преобразуется к известному: $$z_{tc}={\frac {2c'}{\gamma \tan {(45^{o}-\phi '/2)}}}$$

Вывод давления покоя грунта по коэффициенту активного давления грунта

Собственно, это и было предусмотрено в EM1110-2-2502. с применением коэффициента мобилизации силы (SMF) к c' и tanφ'. Согласно данному Руководству инженера, подходящее значение SMF позволяет рассчитать давление грунта, превышающее активное, с использованием уравнения активной силы Кулона. Приняв среднее значение SMF, равное 2/3 вдоль кулоновской поверхности разрушения, было показано, что для чисто фрикционных грунтов полученное значение коэффициента давления грунта довольно хорошо совпадает с соответствующим значением, полученным из расчета Джаки. $K_{0}=1-\sin \phi '$ уравнение.

В решении, предложенном Пантелидисом, фактор SMF – это $1/f_{m}$ соотношение и то, что было предусмотрено EM1110-2-2502, можно точно рассчитать.

Пример №1: Для $c'$=20 кПа, $\phi '$=30 ^тот , γ=18 кН/м ³ , $k_{h}$= $k_{v}$=0, и $z$=2 м, для состояния покоя $K_{0}$=0.211, $c_{m}$=9,00 кПа и $\phi _{m}$=14.57 ^тот . Используя это ( $c_{m}$, $\phi _{m}$) пара значений вместо ( $c'$, $\phi '$) пара значений коэффициента активного давления грунта ( ${\textstyle K_{ae}}$), указанный ранее, последний возвращает коэффициент давления грунта, равный 0,211, то есть коэффициент давления грунта в состоянии покоя.

Пример №2: Для $c'$=0 кПа, $\phi '$=30 ^тот , γ=18 кН/м ³ , $k_{h}$=0.3, $k_{v}$=0,15, и $z$=2 м, для состояния покоя $K_{oe}$=0.602, $c_{m}$=0 кПа и $\phi _{m}$=14.39 ^тот . Используя это ( $c_{m}$, $\phi _{m}$) пара значений вместо ( $c'$, $\phi '$) пара значений и $k_{h}$= $k_{v}$=0 в коэффициенте активного давления грунта ( ${\textstyle K_{ae}}$), указанный ранее, последний возвращает коэффициент давления грунта, равный 0,602, то есть снова коэффициент давления грунта в состоянии покоя.

Сравнение методов Еврокода 8-5 и AASHTO для анализа давления грунта с испытаниями на центрифуге, методом конечных элементов и обобщенными коэффициентами давления грунта.

Исчерпывающее сравнение методов измерения давления грунта, включенных в стандарты EN1998-5:2004 (использование метода Мононобе-Окабе, MO), prEN1998-5:2021 и AASHTO (MO с полупиковым ускорением грунта), с современными центрифужными испытаниями, методом конечных элементов. и обобщенные коэффициенты давления грунта был осуществлен Пантелидисом и Христодулу. Последние включают, среди прочего, результаты 157 численных случаев с использованием двух программ конечных элементов (Rocscience RS2 и mrearth2d) и двух различных современных исследований по испытаниям на центрифугах.

См. также

• Теория Мора-Кулона
• Механика грунтов

Ссылки

• Кодуто, Дональд (2001), Foundation Design , Прентис-Холл, ISBN  0-13-589706-8
• Материалы Министерства транспорта Калифорнии о боковом давлении грунта