Анализ устойчивости склона

Метод срезов

Анализ устойчивости склонов - это статический или динамический, аналитический или эмпирический метод оценки устойчивости откосов грунтовых и каменно-насыпных плотин, насыпей, выкопанных откосов и естественных откосов в почве и скалах. Он выполняется для оценки безопасности проектирования искусственных или естественных склонов (например , насыпей , выемок дорог , открытых горных работ , раскопок, свалок и т. д.) и условий равновесия. Устойчивость склона – это устойчивость наклонной поверхности к разрушению в результате скольжения или обрушения. Основными задачами анализа устойчивости склонов являются поиск зон, находящихся под угрозой исчезновения, исследование потенциальных механизмов отказа, определение чувствительности склона к различным пусковым механизмам, проектирование оптимальных склонов с точки зрения безопасности , надежности и экономики , а также разработка возможных мер по исправлению положения, например, барьеров и стабилизация .

Для успешного проектирования склона необходима геологическая информация и характеристики площадки, например, свойства почвы / горной массы, геометрия склона , состояние грунтовых вод , чередование материалов в результате разломов , трещин или разрывов систем , движений и напряжений в суставах, сейсмической активности и т. д. Наличие воды отрицательно влияет на устойчивость склона. Давление воды, действующее в поровых пространствах, трещинах или других неоднородностях материалов, составляющих откос карьера, снижает прочность этих материалов. Выбор правильного метода анализа зависит как от условий на месте, так и от потенциального характера отказа, при этом тщательное внимание уделяется различным сильным и слабым сторонам и ограничениям, присущим каждой методологии .

До компьютерного возраста анализ стабильности проводился графически или с помощью ручного калькулятора. Сегодня у инженеров есть много возможностей использовать программное обеспечение для анализа , начиная от простых методов предельного равновесия и заканчивая подходами к вычислительному анализу пределов (например, анализ пределов конечных элементов , оптимизация схемы разрывов ) и заканчивая сложными и сложными численными решениями ( коды конечных / отдельных элементов). . Инженер должен полностью понимать ограничения каждого метода. Например, предельное равновесие является наиболее часто используемым и простым методом решения, но он может стать неадекватным, если склон разрушается по сложным механизмам (например, внутренняя деформация и хрупкое разрушение , прогрессирующая ползучесть , разжижение более слабых слоев грунта и т. д.). В этих случаях численного моделирования следует использовать более сложные методы . Кроме того, даже для очень простых наклонов результаты, полученные с помощью типичных методов предельного равновесия, используемых в настоящее время (Бишоп, Спенсер и т. д.), могут значительно отличаться. использование концепции оценки рисков Кроме того, сегодня расширяется . Оценка риска касается как последствий разрушения склона, так и вероятности разрушения (оба требуют понимания механизма разрушения).

Анализ предельного равновесия

Типичное сечение уклона, используемое в двумерном анализе.

Традиционные методы анализа устойчивости склонов можно разделить на три группы: кинематический анализ, анализ предельного равновесия и камнепадов симуляторы . для анализа устойчивости склонов Большинство компьютерных программ основаны на концепции предельного равновесия для двух- или трехмерной модели. Двумерные сечения анализируются в предположении условий плоской деформации . Анализ устойчивости двумерной геометрии склонов с использованием простых аналитических подходов может дать важную информацию о первоначальном проектировании и оценке рисков откосов.

Методы предельного равновесия исследуют равновесие грунтового массива, стремящегося сползти вниз под действием силы тяжести . Поступательное или вращательное движение рассматривается на предполагаемой или известной потенциальной поверхности скольжения под почвой или горной массой. При проектировании горных склонов методы могут иметь большое значение для простого разрушения блоков вдоль отдельных разрывов. Все эти методы основаны на сравнении сил , моментов или напряжений, сопротивляющихся движению массы, с теми, которые могут вызвать неустойчивое движение (возмущающие силы). Результатом анализа является коэффициент безопасности , определяемый как отношение прочности на сдвиг (или, альтернативно, эквивалентной меры сопротивления сдвигу или емкости) к напряжению сдвига (или другой эквивалентной мере), необходимому для равновесия. Если значение коэффициента запаса меньше 1,0, наклон неустойчив.

Все методы предельного равновесия предполагают, что на сдвиг прочность материалов вдоль потенциальной поверхности разрушения определяется линейными ( Мора-Кулона ) или нелинейными соотношениями между прочностью на сдвиг и нормальным напряжением на поверхности разрушения. Наиболее часто используемым вариантом является Терзаги теория прочности на сдвиг , которая утверждает, что

$\tau =\sigma '\tan \phi '+c'$

где $\tau$ - прочность границы раздела на сдвиг, $\sigma '=\sigma -u$ – эффективное напряжение ( $\sigma$ общее напряжение, нормальное к интерфейсу и $u$ поровое давление воды на границе раздела), $\phi '$ - эффективный угол трения, а $c'$ это эффективная сплоченность.

Метод срезов является наиболее популярным методом предельного равновесия. В этом подходе почвенная масса дискретизируется на вертикальные срезы. Используются несколько вариантов метода. Эти вариации могут давать разные результаты (коэффициент запаса прочности) из-за разных предположений и граничных условий между срезами.

Местоположение интерфейса обычно неизвестно, но его можно найти с помощью методов численной оптимизации. Например, При проектировании функционального уклона поверхность скольжения рассматривается критическая как место, где она имеет наименьшее значение коэффициента безопасности из ряда возможных поверхностей. В широком спектре программного обеспечения для стабилизации склонов используется концепция предельного равновесия с автоматическим определением критической поверхности скольжения.

Типичное программное обеспечение для обеспечения устойчивости склонов может анализировать устойчивость обычно слоистых грунтовых откосов, насыпей, выемок земли и закрепленных настилов . Также могут быть включены эффекты землетрясения, внешняя нагрузка , состояние грунтовых вод, силы стабилизации (т.е. якоря, геоармирование и т. д.).

Аналитические методы: метод срезов.

Схема метода срезов с указанием центра вращения.

Многие инструменты анализа устойчивости склонов используют различные версии методов срезов, таких как упрощенный метод Бишопа , обычный метод срезов ( метод шведского круга/Петтерсона/Феллениуса ), Спенсера , Сармы и т. д. Сарма и Спенсер называются строгими методами, поскольку они удовлетворяют всем трем условиям. равновесия: равновесие сил в горизонтальном и вертикальном направлении и состояние равновесия моментов. Строгие методы могут дать более точные результаты, чем нестрогие. Упрощенный метод Бишопа или метод Феллениуса — это нестрогие методы, удовлетворяющие лишь некоторым условиям равновесия и делающие некоторые упрощающие предположения. Некоторые из этих подходов обсуждаются ниже.

Шведский метод анализа скользящего круга

Шведский метод круга скольжения предполагает, что угол трения грунта или породы равен нулю, т.е. $\tau =c'$. Другими словами, когда угол трения считается равным нулю, член эффективного напряжения обращается в ноль, таким образом приравнивая прочность на сдвиг к параметру сцепления данного грунта. Шведский метод круга скольжения предполагает наличие круговой границы разрушения и анализирует параметры напряжения и прочности с использованием круговой геометрии и статики. Момент, вызванный внутренними движущими силами склона, сравнивается с моментом, вызванным силами, противодействующими разрушению склона. Если силы сопротивления превышают движущие силы, наклон считается стабильным.

Обычный метод срезов

Деление наклонной массы методом срезов.

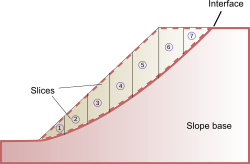
В методе срезов, также называемом OMS или методом Феллениуса, скользящая масса над поверхностью разрушения делится на несколько срезов. Силы, действующие на каждый срез, получаются путем рассмотрения механического (силового и моментного) равновесия срезов. Каждый срез рассматривается отдельно, а взаимодействием между срезами пренебрегают, поскольку результирующие силы параллельны основанию каждого среза. Однако этот метод не удовлетворяет третьему закону Ньютона, поскольку, как правило, результирующие значения слева и справа от среза не имеют одинаковой величины и не коллинеарны.

Это позволяет провести простой расчет статического равновесия, учитывая только вес грунта, а также сдвиговые и нормальные напряжения вдоль плоскости разрушения. Для каждого среза можно учитывать как угол трения, так и сцепление. В общем случае метода срезов силы, действующие на срез, показаны на рисунке ниже. Нормальный( $E_{r},E_{l}$) и сдвиг ( $S_{r},S_{l}$) силы между соседними срезами ограничивают каждый срез и делают задачу статически неопределенной, когда они включаются в вычисление.

Силовое равновесие среза в методе срезов. Предполагается, что блок имеет толщину $b$. На срезы слева и справа действуют нормальные силы. $E_{l},E_{r}$ и поперечные силы $S_{l},s_{r}$, вес ломтика вызывает силу $W$. Эти силы уравновешиваются поровым давлением и реакциями основания. $N,T$.

Для обычного метода срезов результирующие вертикальные и горизонтальные силы равны

${\begin{aligned}\sum F_{v}=0&=W-N\cos \alpha -T\sin \alpha \\\sum F_{h}=0&=kW+N\sin \alpha -T\cos \alpha \end{aligned}}$

где $k$ представляет собой линейный коэффициент, определяющий увеличение горизонтальной силы с глубиной среза. Решение для $N$ дает

$N=W\cos \alpha -kW\sin \alpha \,.$

Далее, метод предполагает, что каждый срез может вращаться вокруг центра вращения и что баланс моментов вокруг этой точки также необходим для равновесия. Баланс моментов для всех срезов, взятых вместе, дает

$\sum M=0=\sum _{j}(W_{j}x_{j}-T_{j}R_{j}-N_{j}f_{j}-kW_{j}e_{j})$

где $j$ индекс среза, $x_{j},R_{j},f_{j},e_{j}$ являются плечами момента, а нагрузки на поверхности не учитываются. Уравнение момента можно использовать для определения поперечных сил на границе раздела после подстановки выражения для нормальной силы:

$\sum _{j}T_{j}R_{j}=\sum _{j}[W_{j}x_{j}-(W_{j}\cos \alpha _{j}-kW_{j}\sin \alpha _{j})f_{j}-kW_{j}e_{j}]$

Используя теорию прочности Терцаги и преобразуя напряжения в моменты, мы имеем

$\sum _{j}\tau l_{j}R_{j}=l_{j}R_{j}\sigma _{j}'\tan \phi '+l_{j}R_{j}c'=R_{j}(N_{j}-u_{j}l_{j})\tan \phi '+l_{j}R_{j}c'$

где $u_{j}$ это поровое давление.Коэффициент запаса прочности - это отношение максимального момента по теории Терзаги к расчетному моменту,

${\text{Factor of safety}}={\frac {\sum _{j}\tau l_{j}R_{j}}{\sum _{j}T_{j}R_{j}}}\,.$

Модифицированный метод анализа Бишопа

Модифицированный метод Бишопа немного отличается от обычного метода срезов тем, что нормальные силы взаимодействия между соседними срезами считаются коллинеарными, а результирующая сила сдвига между срезами равна нулю. Этот подход был предложен Аланом В. Бишопом из Имперского колледжа . Ограничение, введенное нормальными силами между срезами, делает задачу статически неопределимой. В результате для расчета коэффициента безопасности приходится использовать итерационные методы. Было показано, что этот метод дает значения коэффициента безопасности в пределах нескольких процентов от «правильных» значений.

Фактор запаса прочности моментного равновесия в методе Бишопа можно выразить как

$F={\cfrac {\sum _{j}{\cfrac {\left[c'l_{j}+(W_{j}-u_{j}l_{j})\tan \phi '\right]}{\psi _{j}}}}{\sum _{j}W_{j}\sin \alpha _{j}}}$

где

$\psi _{j}=\cos \alpha _{j}+{\frac {\sin \alpha _{j}\tan \phi '}{F}}$

где, как и прежде, $j$ индекс среза, $c'$ это эффективная сплоченность, $\phi '$ – эффективный внутренний угол внутреннего трения, $l$ ширина каждого среза, $W$- вес каждого ломтика, а $u$ — давление воды у основания каждого среза. Для решения задачи необходимо использовать итерационный метод. $F$ потому что коэффициент безопасности появляется как в левой, так и в правой частях уравнения.

метод Лоримера

Метод Лоримера — это метод оценки устойчивости склонов в связных грунтах. Он отличается от метода Бишопа тем, что в нем используется клотоидная вместо круга поверхность скольжения. Этот вид разрушения был определен экспериментально для учета эффектов цементации частиц. Метод был разработан в 1930-х годах Герхардтом Лоримером (20 декабря 1894 — 19 октября 1961), учеником пионера геотехники Карла фон Терцаги .

Метод Спенсера

Метод анализа Спенсера требуется компьютерная программа, поддерживающая циклические алгоритмы, но облегчающая анализ устойчивости склона. Алгоритм Спенсера удовлетворяет всем состояниям равновесия (горизонтальному, вертикальному и движущему моменту) на каждом срезе. Метод учитывает неограниченные плоскости скольжения и, следовательно, позволяет определить коэффициент запаса прочности вдоль любой поверхности скольжения. Жесткое равновесие и неограниченная поверхность скольжения обеспечивают более точные коэффициенты запаса, чем, например, метод Бишопа или обычный метод срезов.

Метод Сармы

Основная статья: Метод Сармы

Метод Сармы , предложенный Сарадой К. Сармой из Имперского колледжа , это метод предельного равновесия, используемый для оценки устойчивости склонов в сейсмических условиях. Его также можно использовать для статических условий, если значение горизонтальной нагрузки принять равным нулю. Этот метод позволяет анализировать широкий спектр разрушений на склонах, поскольку он может учитывать механизм разрушения с несколькими клиньями и, следовательно, не ограничивается плоскими или круглыми поверхностями разрушения. Он может предоставить информацию о факторе безопасности или о критическом ускорении, необходимом для того, чтобы вызвать обрушение.

Сравнения

Допущения, сделанные с помощью ряда методов предельного равновесия, перечислены в таблице ниже.

Метод	Предположение
Обычный метод срезов	Межсрезовые силы не учитываются.
Упрощенный/модифицированный Бишоп	Результирующие силы между срезами горизонтальны. Силы сдвига между срезами отсутствуют.
Джанбу упрощенный	Результирующие силы между срезами горизонтальны. Эмпирический поправочный коэффициент используется для учета сил сдвига между срезами.
Обобщенный Джанбу	Предполагаемая линия тяги используется для определения местоположения нормальной силы между срезами.
Спенсер	Результирующие межсрезные силы имеют постоянный наклон по всей скользящей массе. Линия тяги – это степень свободы.
чух	То же, что метод Спенсера, но с постоянной силой ускорения на каждом срезе.
Моргенштерн-Прайс	Направление результирующих сил между срезами определяется с помощью произвольной функции. Вычисляются доли значения функции, необходимые для баланса сил и моментов.
Фредлунд-Кран (GLE)	Похоже на: Моргенштерн-Прайс.
Инженерный корпус	Результирующая межсрезная сила либо параллельна поверхности земли, либо равна среднему уклону от начала до конца поверхности скольжения.
Лоу и Карафиат	Направление результирующей силы между срезами равно среднему значению поверхности земли и наклону основания каждого среза.
Сарма	Критерий прочности на сдвиг применяется к сдвигам по бокам и снизу каждого среза. Наклоны границ разделов изменяются до тех пор, пока не будет достигнут критический критерий.

В таблице ниже показаны условия статического равновесия, которым удовлетворяют некоторые популярные методы предельного равновесия.

Метод	Баланс сил (вертикальный)	Баланс сил (горизонтальный)	Моментный баланс
Обычный МС	Да	Нет	Да
упрощенная версия епископа	Да	Нет	Да
Джанбу упрощенный	Да	Да	Нет
Обобщенный Джанбу	Да	Да	Используется для расчета сил сдвига между срезами.
Спенсер	Да	Да	Да
чух	Да	Да	Да
Моргенштерн-Прайс	Да	Да	Да
Фредлунд-Кран	Да	Да	Да
Инженерный корпус	Да	Да	Нет
Лоу и Карафиат	Да	Да	Нет
Сарма	Да	Да	Да

Анализ устойчивости скальных склонов

Анализ устойчивости горных откосов, основанный на методах предельного равновесия, может учитывать следующие виды отказов:

• Плоское разрушение -> случай скольжения горной массы по одной поверхности (частный случай общего клинового разрушения); двумерный анализ может быть использован в соответствии с концепцией сопротивления блока на наклонной плоскости при предельном равновесии.
• Полигональное разрушение -> скольжение природных камней обычно происходит по многоугольной формы поверхностям ; расчет основан на определенных допущениях (например, скольжение по многоугольной поверхности, составленной из N частей, кинематически возможно только в случае развития не менее (N - 1) внутренних поверхностей сдвига; горная порода разделена на блоки внутренними поверхностями сдвига; блоки считаются жесткими; предел прочности на растяжение не допускается и т. д.).
• Разрушение клина -> трехмерный анализ позволяет моделировать скольжение клина в двух плоскостях в направлении вдоль линии пересечения.
• Обрушение -> длинные тонкие колонны породы, образованные крутопадающими разрывами, могут вращаться вокруг точки поворота, расположенной в самом нижнем углу блока; сумма моментов, вызывающих опрокидывание блока (т.е. горизонтальная составляющая веса блока и сумма движущих сил соседних блоков за рассматриваемым блоком) сравнивается с суммой моментов, сопротивляющихся опрокидыванию (т.е. вертикальная составляющая веса блок и сумма сил сопротивления соседних блоков перед рассматриваемым блоком); опрокидывание происходит, если движущие моменты превышают моменты сопротивления

Предельный анализ

См. Также: Устойчивость склона.

Более строгий подход к анализу устойчивости склона – это анализ пределов . В отличие от анализа предельного равновесия, который делает специальные, хотя зачастую разумные предположения, предельный анализ основан на строгой теории пластичности. Это позволяет, среди прочего, вычислить верхнюю и нижнюю границы истинного коэффициента запаса прочности.

Программы, основанные на анализе лимитов, включают в себя:

• OptumG2 (2014-) Программное обеспечение общего назначения для геотехнических приложений (также включает упругопластичность, просачивание, консолидацию, поэтапное строительство, прокладку туннелей и другие соответствующие типы геотехнического анализа).
• LimitState:GEO (2008-) Геотехническое программное обеспечение общего назначения, основанное на оптимизации схемы разрывов для решения проблем плоской деформации, включая устойчивость склонов.

Стереографический и кинематический анализ

См. Также: Стереонет § Геология

Кинематический анализ исследует, какие виды разрушения могут возникнуть в массиве горных пород. Анализ требует детальной оценки структуры горного массива и геометрии существующих неоднородностей, способствующих нестабильности блоков . Используется стереографическое изображение ( стереосети ) плоскостей и линий. Стереосети полезны для анализа прерывистых блоков горных пород. Программа DIPS позволяет осуществлять визуализацию структурных данных с помощью стереосетей, определение кинематической целесообразности горного массива и статистический анализ свойств неоднородностей.

Симуляторы камнепада

Анализ устойчивости скальных откосов может помочь разработать защитные меры вблизи или вокруг сооружений, которым угрожают падающие блоки. Симуляторы камнепада определяют траектории перемещения нестабильных блоков, отделившихся от скального склона. Метод аналитического решения, описанный Hungr & Evans предполагает каменный блок как точку с массой и скоростью, движущуюся по баллистической траектории с учетом потенциального контакта с поверхностью склона. Для расчета необходимы два коэффициента восстановления, которые зависят от формы фрагмента, шероховатости поверхности склона, импульсных и деформационных свойств, а также от вероятности наступления определенных условий при данном ударе.

Численные методы анализа

Методы численного моделирования обеспечивают приближенное решение проблем, которые иначе не могут быть решены обычными методами, например, сложная геометрия, анизотропия материала , нелинейное поведение, напряжения на месте. Численный анализ позволяет проводить деформацию и разрушение материала, моделировать поровое давление , деформацию ползучести , динамическую нагрузку, оценивать влияние изменений параметров и т. д. Однако численное моделирование ограничено некоторыми ограничениями. Например, входные параметры обычно не измеряются, а доступность этих данных обычно неудовлетворительна. Пользователь также должен знать о граничных эффектах, ошибках построения сетки, аппаратной памяти и ограничениях по времени. Численные методы, используемые для анализа устойчивости склонов, можно разделить на три основные группы: континуальное , дискретное и гибридное моделирование.

Континуальное моделирование

См. также: Метод конечных элементов и Метод конечных разностей.

Рисунок 3: Сетка конечных элементов

Моделирование континуума подходит для анализа почвенных склонов, массивных неповрежденных горных пород или массивов горных пород с сильными трещинами. Этот подход включает в себя конечных разностей и конечных элементов методы , которые дискретизируют всю массу до конечного числа элементов с помощью сгенерированной сетки (рис. 3). В методе конечных разностей (FDM) дифференциальные уравнения равновесия (т.е. соотношения деформации-перемещения и напряжения-деформации решаются ). Метод конечных элементов (МКЭ) использует приближения к связности элементов, непрерывности перемещений и напряжений между элементами. Большинство числовых кодов позволяют моделировать дискретные трещины , например, плоскости напластования , разломы . Обычно доступно несколько конститутивных моделей, например эластичность , упругопластичность, размягчение деформации, упруговязкопластичность и т. д.

Дисконтинуальное моделирование

См. также: Метод дискретных элементов и анализ разрывной деформации.

Подход разрыва полезен для склонов горных пород, контролируемых неоднородностями. Горный массив рассматривается как совокупность отдельных взаимодействующих блоков, подвергающихся внешним нагрузкам и предположительно находящихся в движении со временем. Эта методология в совокупности называется методом дискретных элементов (МДЭ). Моделирование дисконтинуума позволяет скользить между блоками или частицами. ЦМР основана на многократном решении динамического уравнения равновесия для каждого блока до тех пор, пока не будут выполнены граничные условия и законы контакта и движения . Моделирование разрыва относится к наиболее часто применяемому численному подходу к анализу откосов горных пород, и существуют следующие варианты ЦМР:

• метод отдельных элементов
• Анализ прерывистой деформации (DDA)
• коды потока частиц

Подход отдельных элементов описывает механическое поведение как разрывов, так и твердого материала. Эта методика основана на законе силы-перемещения (определяющем взаимодействие между деформируемыми блоками породы) и законе движения (определяющем перемещения, вызванные в блоках дисбалансными силами). Соединения рассматриваются как [граничные условия. Деформируемые блоки дискретизируются на внутренние элементы постоянной деформации.

Прерывистая программа UDEC (Универсальный отдельный код элемента) подходит для скальных откосов с высокими трещинами, подвергающихся статическим или динамическим нагрузкам. Двумерный анализ механизма поступательного разрушения позволяет моделировать большие перемещения, моделировать деформацию или текучесть материала. Трехмерный дискретный код 3DEC содержит моделирование множества пересекающихся разрывов и поэтому подходит для анализа нестабильности клина или влияния крепи горной породы (например, анкерных болтов, тросов).

В анализе разрывной деформации (DDA) смещения являются неизвестными, и затем уравнения равновесия решаются аналогично методу конечных элементов . Каждая единица сетки типа конечных элементов представляет собой изолированный блок, ограниченный разрывами. Преимуществом этой методологии является возможность моделировать большие деформации, движения твердого тела, состояния сцепления или разрушения между блоками породы.

Прерывистый массив горных пород можно смоделировать с помощью методологии отдельных элементов в виде кода потока частиц , например, программы PFC2D/3D . Сферические частицы взаимодействуют посредством фрикционных скользящих контактов. Моделирование объединенных блоков может быть реализовано за счет заданной прочности связей. Закон движения многократно применяется к каждой частице, а закон силы-перемещения — к каждому контакту. Методология потока частиц позволяет моделировать поток гранул, разрушение неповрежденной породы, движения переходных блоков, динамическую реакцию на взрывные работы или сейсмичность, деформацию между частицами, вызванную силами сдвига или растяжения. Эти коды также позволяют моделировать последующие процессы разрушения склона горной породы, например, моделирование

Гибридное/связанное моделирование

Гибридные кодексы предполагают объединение различных методологий для максимизации их ключевых преимуществ, например, анализ предельного равновесия в сочетании с анализом потоков грунтовых вод методом конечных элементов и анализом напряжений; анализ связанных потоков частиц и анализ конечных разностей ; гидромеханически связанные методы конечных элементов и материальных точек для моделирования всего процесса оползней, вызванных дождями. Гибридные методы позволяют исследовать провалы откосов трубопроводов и влияние высокого давления грунтовых вод на провалы слабых откосов горных пород. Связанные коды с конечными различными элементами позволяют моделировать как поведение неповрежденной породы, так и развитие и поведение трещин.

См. также

• Анализ прерывистой деформации
• Оптимизация компоновки разрывов
• Метод дискретных элементов
• Метод конечных разностей
• Предельный анализ методом конечных элементов
• Метод конечных элементов
• Теория Мора-Кулона
• ПЛАКСИС
• Классификация СМР
• Стереонет

Дальнейшее чтение

• Витек, Б. (2021). Откосы и котлованы - Проектирование и расчет . Спрингер Вьюег . п. 381. ИСБН  978-3-658-35852-5 .
• Девото, С.; Кастелли, Э. (сентябрь 2007 г.). Устойчивость склона в старом известняковом карьере, заинтересованном в туристическом проекте . 15-е заседание Ассоциации европейских геологических обществ: георесурсная политика, менеджмент, окружающая среда. Таллинн.
• Дау, В. (2009). Разработка схемы использования массовых гравитационных движений при добыче кварцитов в Рейнских Сланцевых горах . Хакенхайм, Германия: ConchBooks. п. 358. ИСБН  978-3-939767-10-7 .
• Хак, HRGK (25–28 ноября 2002 г.). «Оценка классификации устойчивости склонов. Основная лекция». В Динише да Гаме, К.; Рибейра и Соуза, Л. (ред.). Учеб. ИСРМ ЕВРОК'2002 . Фуншал, Мадейра, Португалия: Португальское геотехническое общество, Лиссабон, Португалия. стр. 3–32. ISBN  972-98781-2-9 .
• Лю, Ю.-К.; Чен, К.-С. (2005). «Новый подход к применению классификации горных пород при оценке устойчивости горных откосов». Инженерная геология . 89 (1–2): 129–143. дои : 10.1016/j.enggeo.2006.09.017 .
• Пантелидис, Л. (2009). «Оценка устойчивости горных откосов с помощью систем классификации горных массивов». Международный журнал механики горных пород и горных наук . 46 (2, номер 2): 315–325. Бибкод : 2009IJRMM..46..315P . дои : 10.1016/j.ijrmms.2008.06.003 .
• Рупке, Дж.; Хейсман, М.; Крузе, HMG (2007). «Устойчивость искусственных склонов». Инженерная геология . 91 (1): 16–24. Бибкод : 2007EngGe..91...16R . дои : 10.1016/j.enggeo.2006.12.009 .
• Сингх, Б.; Гоэл, РК (2002). Программное обеспечение для инженерного контроля оползневой и туннельной опасности . Том. 1. Тейлор и Фрэнсис . п. 358. ИСБН  978-90-5809-360-8 .

• Кодуто, Дональд П. (1998). Геотехническая инженерия: принципы и практика. Прентис-Холл. ISBN   0-13-576380-0
• Фредлунд, Д.Г., Х. Рахарджо, доктор медицинских наук Фредлунд (2014). Механика ненасыщенных грунтов в инженерной практике. Уайли-Интерсайенс. ISBN   978-1118133590
• Кличе, Чарльз А. (1999), Устойчивость горных склонов , Колорадо, США: Общество горнодобывающей промышленности, металлургии и геологоразведки, ISBN  0-87335-171-1
• Эберхардт, Эрик (2003), Анализ устойчивости горных склонов - использование передовых численных методов (PDF) , Ванкувер, Канада: Науки о Земле и океане, Университет Британской Колумбии
• Инженерный корпус армии США (2003 г.), Проектирование и проектирование - устойчивость склонов (PDF) , Вашингтон, округ Колумбия, США: Инженерный корпус армии США
• Стед, Дуг; Эберхардт, Э.; Когган, Дж.; Бенко, Б. (2001). М. Кюне; Его Святейшество Эйнштейн; Э. Краутер; Х. Клапперих; Р. Пёттлер (ред.). Передовые численные методы анализа устойчивости горных откосов — Приложения и ограничения (PDF) . Международная конференция UEF по оползням: причины, последствия и меры противодействия. Давос, Швейцария: Verlag Glückauf GmbH. стр. 615–624.
• Абрамсон, Ли В.; Ли, Томас С.; Шарма, Сунил; Бойс, Гленн М. (2002), Устойчивость склона и методы стабилизации (2-е изд.), Нью-Йорк, США: John Wiley & Sons, ISBN  0-471-38493-3
• Чжу, Д.Ю.; Ли, CF; Цзян, Х.Д. (2003), «Обобщенная структура методов предельного равновесия для анализа устойчивости склонов», Geotechnique , 53 (4), Телфорд, Лондон, Великобритания: 377–395, Bibcode : 2003Getq...53..377Z , doi : 10.1680/geot.2003.53.4.377 , hdl : 10722/71758 , ISSN   0016-8505
• Ковари, Кальман; Фриц, П. (1978). Устойчивость склона с плоскими, клиновыми и многоугольными поверхностями скольжения . Международный симпозиум по механике горных пород, посвященный фундаментам плотин. Рио-де-Жанейро, Бразилия. стр. 103–124.
• Ян, Сяо-Ли; Ли, Л.; Инь, Дж. Х. (2004), «Анализ устойчивости горных пород с модифицированным критерием разрушения Хука-Брауна», Международный журнал численных и аналитических методов в геомеханике , 28 (2), Чичестер, Великобритания: John Wiley & Sons: 181– 190, Bibcode : 2004IJNAM..28..181Y , doi : 10.1002/nag.330 , ISSN   0363-9061 , S2CID   120421002
• Бартон, Северная Каролина; Бандис, Южная Каролина (1990). «Обзор прогнозирующих возможностей модели JRC-JCS в инженерной практике» . В Бартоне, Ник (ред.). Скальные соединения . Международный симпозиум по соединениям горных пород. Роттердам: Балкема. стр. 603–610. ISBN  978-90-6191-109-8 .
• Хунгр, О.; Эванс, С.Г. (1988). «Инженерная оценка опасности обломочных камнепадов». В Боннаре, К. (ред.). Оползни . Международный симпозиум по оползням, Лозанна. Роттердам: Балкема. стр. 685–690.

Внешние ссылки

• Геотехническое программное обеспечение в Curlie