Аналемма

О книге Птолемея см. Аналемма (Птолемей) . Более общее значение графической процедуры см. в разделе Ортографическая проекция .

Послеобеденная фотография аналеммы, сделанная Джеком Фишберном в 1998–1999 годах в Мюррей-Хилл, штат Нью-Джерси, США. На переднем плане здание Bell Laboratories.

Аналемма с отметками даты, напечатанная на глобусе, Музей глобуса , Вена, Австрия.

В астрономии ( — аналемма / ˌ æ n ə ˈ l ɛ m ə / ; от древнегреческого ἀνάλημμα (analēmma) 'поддержка'). Это диаграмма, показывающая положение Солнца на небе , как видно из фиксированного места на Земле в одно и то же среднее солнечное время , поскольку это положение меняется в течение года . Схема будет напоминать восьмерку . На земных шарах часто отображается аналемма в виде двумерной фигуры уравнения времени и склонения Солнца.

Компонент аналеммы с севера на юг возникает в результате изменения склонения Солнца из-за наклона Земли оси вращения при ее вращении вокруг Солнца. Компонент восток-запад является результатом неравномерной скорости изменения Солнца прямого восхождения , определяемой совместным воздействием наклона оси Земли и эксцентриситета ее орбиты .

можно сфотографировать, Аналемму удерживая камеру в фиксированном месте и в фиксированной ориентации и делая несколько экспозиций в течение года, всегда в одно и то же время суток (не учитывая летнее время ).

Аналеммы (в современном смысле этого слова) использовались вместе с солнечными часами с 18 века для преобразования видимого и среднего солнечного времени. До этого этот термин имел более общее значение, которое относилось к графической процедуре представления трехмерных объектов в двух измерениях , теперь известной как ортогональная проекция .

Хотя термин «аналемма» обычно относится к солнечной аналемме Земли, его можно применять к другим небесным телам и .

Описание

Аналемма на Земле, поскольку Солнце находится прямо над головой каждые 24 часа в течение года.

Солнца Аналемму можно отследить, построив график положения Солнца, если смотреть из фиксированной точки на Земле, в одно и то же время каждый день в течение всего года или построив график склонения в зависимости от уравнения времени . Получающаяся кривая напоминает длинную стройную восьмерку, у которой одна доля намного больше другой. Эту кривую обычно печатают на земных глобусах , обычно в восточной части Тихого океана, единственном большом тропическом регионе с очень небольшой территорией. Сфотографировать аналемму можно, хотя и сложно, оставив камеру в фиксированном положении на целый год и делая снимки с 24-часовыми интервалами (или с интервалами, кратными им); см. раздел ниже.

Длинная ось фигуры — отрезок линии, соединяющий самую северную точку аналеммы с самой южной — разделена пополам небесным экватором , к которому она примерно перпендикулярна , и имеет «длину», в два раза превышающую наклон эклиптики , т. е. , около 47°. Компонента видимого движения Солнца вдоль этой оси является результатом известного сезонного изменения склонения Солнца в течение года. «Ширина» фигуры обусловлена ​​уравнением времени, а ее угловая протяженность — это разница между наибольшими положительными и отрицательными отклонениями местного солнечного времени от местного среднего времени, когда эта разница во времени связана с углом со скоростью 15° в час, т.е. 360° за 24 часа. Ширина аналеммы составляет примерно 7,7°, поэтому длина фигуры более чем в шесть раз превышает ее ширину. Разница в размерах долей восьмерочной формы возникает главным образом из-за того, что перигелий и афелий располагаются далеко от точек равноденствия . Они также происходят всего через пару недель после солнцестояний , что, в свою очередь, вызывает небольшой наклон восьмерки и ее незначительную боковую асимметрию.

Есть три параметра, которые влияют на размер и форму аналеммы — наклон , эксцентриситет и угол между точкой северного равноденствия и перицентром . Если смотреть с объекта с идеально круглой орбитой и без наклона оси, Солнце всегда будет появляться в одной и той же точке неба в одно и то же время суток в течение года, а аналемма будет представлять собой точку. Для объекта с круговой орбитой, но значительным осевым наклоном аналемма будет иметь форму восьмерки с равными по размеру северной и южной долями. Для объекта с эксцентричной орбитой, но без наклона оси, аналемма будет представлять собой прямую линию восток-запад вдоль небесного экватора.

Компонент аналеммы с севера на юг показывает склонение Солнца , его широту на небесной сфере или широту на Земле, на которой Солнце находится прямо над головой. Компонент восток-запад показывает уравнение времени или разницу между солнечным временем и местным средним временем . Это можно интерпретировать как то, насколько «впереди» или «позади» Солнца (или аналемматических солнечных часов ) по сравнению с временем часов. Он также показывает, насколько далеко на западе или востоке находится Солнце по сравнению с его средним положением. Аналемму можно рассматривать как график, на котором показаны склонение Солнца и уравнение времени. Во многие диаграммы аналеммы также включено третье измерение, измерение времени, которое показано метками, обозначающими положение Солнца в различные, довольно близко расположенные даты в течение года.

На диаграммах аналемма изображается такой, какой ее видел бы на небе наблюдатель, смотрящий вверх. Если север вверху, запад справа то . Это соответствует знаку уравнения времени, который положителен в западном направлении. Чем дальше на запад находится Солнце по сравнению со своим средним положением, тем более «быстрыми» являются солнечные часы по сравнению с часами. (См. Уравнение времени#Знак уравнения времени .) Если аналемма представляет собой график с положительным склонением (север), нанесенным вверх, положительное уравнение времени (запад) отображается справа. Это обычная ориентация графиков. Когда аналемма отмечена на географическом глобусе, запад в аналемме находится справа, а географические объекты на земном шаре показаны западом слева. Чтобы избежать этой путаницы, было предложено печатать аналеммы на глобусах западом слева, но это делается нечасто, по крайней мере. На практике аналемма настолько почти симметрична, что формы зеркальных изображений нелегко различить, но если присутствуют отметки даты, они идут в противоположных направлениях. Солнце движется на восток по аналемме вблизи солнцестояний. Это можно использовать, чтобы определить, каким образом печатается аналемма. Смотрите изображение выше, при большом увеличении .

Аналемма, включающая изображение солнечного затмения, была названа тутулеммой — термин, придуманный фотографами Дженком Э. Тезелем и Тунч Тезелем на основе турецкого слова, обозначающего затмение.

Как видно с Земли

Аналемма изображена в полдень по Гринвичу из Королевской обсерватории в Гринвиче ( широты 51,48 ° северной долготы ). , 0,0015 ° западной

Из-за наклона оси Земли (23,439 °) и эксцентриситета орбиты Земли относительное расположение Солнца над горизонтом не является постоянным изо дня в день, если наблюдать каждый день в одно и то же время. Если время наблюдения не 12:00 по местному времени, то в зависимости от географической широты эта петля будет наклонена под разными углами.

Рисунок в этом разделе представляет собой пример аналеммы, видимой из северного полушария Земли . Это график положения Солнца в 12:00 в Королевской обсерватории в Гринвиче , Англия ( широты 51,48° северной , 0,0015° западной долготы ) в 2006 году. Горизонтальная ось представляет собой угол азимута в градусах (180°). смотрит на юг). Вертикальная ось — высота над горизонтом в градусах. Первый день каждого месяца показан черным цветом, а дни солнцестояния и равноденствия показаны зеленым. Видно, что равноденствия происходят примерно на высоте φ = 90° − 51,5° = 38,5° , а солнцестояния происходят примерно на высотах φ ± ε, где ε — наклон оси Земли, 23,4°. Аналемма изображена с сильно преувеличенной шириной, что демонстрирует небольшую асимметрию (из-за двухнедельного смещения между апсидами орбиты Земли и точками ее солнцестояний ).

Аналемма ориентирована так, что меньшая петля оказывается к северу от большей петли. На Северном полюсе аналемма будет полностью вертикальной (цифра 8 с маленькой петлей наверху), и будет видна только верхняя ее половина. Направляясь на юг, однажды южнее Полярного круга , вся аналемма станет видимой. Если смотреть в полдень, он продолжает оставаться в вертикальном положении и поднимается выше над горизонтом по мере того, как зритель движется на юг. На экваторе он находится прямо над головой. Дальше на юг он движется к северному горизонту, и тогда его можно увидеть с большей петлей наверху. Если смотреть на аналемму рано утром или вечером, она начнет наклоняться в одну сторону по мере того, как зритель движется на юг от Северного полюса. На экваторе аналемма будет полностью горизонтальной. По мере того как зритель продолжал двигаться на юг, он вращался так, что маленькая петля находилась под большой петлей в небе. Пересекая Южный полярный круг , аналемма, теперь почти полностью перевернутая, начала исчезать, пока только 50%, часть большей петли, не стала видна с высоты. Южный полюс .

См. уравнение времени для более подробного описания характеристик аналеммы с востока на запад.

Фотография

Первая успешная фотография аналеммы была сделана в 1978–79 годах фотографом Деннисом ди Чикко над Уотертауном, штат Массачусетс . Не перемещая камеру, он сделал 44 кадра в одном кадре пленки, причем все они были сняты в одно и то же время суток с разницей как минимум в неделю. Изображение переднего плана и три изображения с длинной выдержкой также были включены в один кадр, в результате чего общее количество экспозиций достигло 48.

Рассчитанные аналеммы

«Венок Аналеммы». Аналеммы рассчитаны с интервалом в 1 час друг от друга для географического центра сопредельных Соединенных Штатов. Серая часть указывает на то, что сейчас ночь.

Хотя фотографирование аналемм может представлять технические и практические проблемы, их можно удобно рассчитать и представить в виде трехмерных графиков для любого заданного места на поверхности Земли.

Идея основана на единичном векторе, начало координат которого зафиксировано в выбранной точке на поверхности Земли, а направление все время указывает на центр Солнца. Если мы вычислим положение Солнца, а именно зенитный угол Солнца и угол азимута Солнца , скажем, с шагом в один час, в течение всего года, голова единичного вектора прочертит 24 аналеммы на единичной сфере с центром в выбранной точка, и эта единичная сфера эквивалентна небесной сфере . Рисунок справа — «венок аналемм», рассчитанный для географического центра сопредельных США .

Аналемма: Уравнение времени и склонения Солнца. Рассчитано на 2020 год по формулам Астрономического альманаха на 2019 год .

Как это часто можно увидеть на глобусе, аналемму также часто изображают как двумерную фигуру уравнения времени в зависимости от склонения Солнца. Соседний рисунок («Аналемма: Уравнение времени...») рассчитывается по алгоритму, представленному в ссылке. который использует формулы, приведенные в Астрономическом альманахе на 2019 год .

Оценка данных о восходе и закате солнца

Если аналемма отмечена так, чтобы показывать положение Солнца на нем через довольно регулярные промежутки времени (например, 1-й, 11-й и 21-й дни каждого календарного месяца ), аналемма суммирует видимое движение Солнца относительно его среднего положения в течение года. . Диаграмма аналеммы с отметкой даты и равными масштабами в направлениях север - юг и восток - запад может использоваться в качестве инструмента для оценки таких величин, как время восхода и захода солнца , которые зависят от положения Солнца. Как правило, выполнение этих оценок зависит от визуализации аналеммы как жесткой структуры на небе, которая движется вокруг Земли с постоянной скоростью, поэтому она восходит и заходит один раз в день, а Солнце медленно движется вокруг нее один раз в год.

В этом процессе задействованы некоторые приближения, в основном использование плоской диаграммы для изображения объектов на небесной сфере, а также использование чертежей и измерений вместо численных расчетов. По этой причине оценки не являются абсолютно точными, но обычно они достаточно хороши для практических целей. Кроме того, они имеют обучающее значение, поскольку в простой наглядной форме показывают, как меняется время восхода и захода солнца.

Самый ранний и поздний восход и закат

Схема аналеммы, смотрящей на восток в Северном полушарии . Показаны даты положения Солнца. Эта аналемма рассчитана на 9 утра, не фотографировалась.

Аналемму можно использовать для определения дат самого раннего и самого позднего восхода и захода солнца в году. Они не происходят в дни солнцестояний .

Что касается изображения моделируемой аналеммы на восточном небе, то самая нижняя точка аналеммы только что поднялась над горизонтом. Если бы Солнце находилось в этой точке, восход Солнца только что произошел бы. Это будет самый поздний восход солнца в году, поскольку все остальные точки аналеммы взойдут раньше. Следовательно, дата последнего восхода солнца — это момент, когда Солнце находится в этой самой низкой точке (29 декабря, когда аналемма наклонена, если смотреть с 50 ° северной широты, как показано на диаграмме); однако в некоторых регионах, где используется летнее время , дата последнего восхода солнца приходится на день до окончания летнего времени. Точно так же, когда Солнце находится в самой высокой точке аналеммы, возле ее верхнего левого конца (15 июня), произойдет самый ранний восход солнца в году. Аналогично, на закате самый ранний закат произойдет, когда Солнце находится в самой низкой точке аналеммы, когда оно находится близко к западному горизонту, а самый поздний закат произойдет, когда оно будет в самой высокой точке.

Ни одна из этих точек не находится точно на одном из концов аналеммы, где Солнце находится в период солнцестояния. Как видно из северных средних широт , как показано на диаграмме, самый ранний закат происходит за некоторое время до декабрьского солнцестояния – обычно за неделю или две до него – а самый поздний восход солнца происходит через неделю или две после солнцестояния. Таким образом, самый темный вечер приходится на начало-середину декабря, но утро продолжает темнеть примерно до Нового года.

График времени восхода солнца в Либревиле , Габон , который находится очень близко к экватору . Обратите внимание, что есть два максимума и два минимума.

Точные даты — это те, в которые Солнце находится в точках, где горизонт касается аналеммы, что, в свою очередь, зависит от того, насколько аналемма, или проходящий через нее меридиан север-юг, наклонена от вертикали. Этот угол наклона по существу равен широте (90 ° минус широта) наблюдателя. Численный расчет этих дат является сложным, но их можно оценить довольно точно, поместив линейку, наклоненную под соответствующим углом, по касательной к диаграмме аналеммы, и прочитав даты (при необходимости интерполируя), когда Солнце находится в позиции контакта.

В средних широтах даты отклоняются дальше от солнцестояний по мере уменьшения абсолютного значения широты. В околоэкваториальных широтах ситуация сложнее. Аналемма лежит почти горизонтально, поэтому горизонт может касаться ее в двух точках, по одной в каждой петле аналеммы. Таким образом, в году есть две сильно разнесенные даты, когда Солнце восходит раньше, чем в соседние дни, и так далее.

Время восхода и захода солнца

Подобный геометрический метод, основанный на аналемме, можно использовать для определения времени восхода и захода солнца в любом месте на Земле (за исключением Полярного или Антарктического круга или вблизи него ) в любую дату.

Начало по аналеммы, где солнечное склонение и уравнение времени равны нулю, восходит и заходит в 6 часов утра и 18 часов вечера местному времени в каждый день года, независимо от широты наблюдателя . (Эта оценка не учитывает атмосферную рефракцию .) Если аналемма нарисована на диаграмме, наклонена под углом, соответствующим широте наблюдателя (как описано выше), и если проведена горизонтальная линия, проходящая через положение Солнце на аналемме в любую дату (при необходимости интерполируя между отметками даты), затем на восходе солнца эта линия представляет собой горизонт.

Кажется, что начало координат движется вдоль небесного экватора со скоростью 15° в час — скорости вращения Земли . Расстояние по небесному экватору от точки его пересечения с горизонтом до положения начала аналеммы при восходе Солнца — это расстояние, на которое перемещается начало координат между 6 часами утра и временем восхода солнца в данную дату. Таким образом, измерение длины этого экваториального сегмента дает разницу между 6 часами утра и временем восхода солнца.

Измерение, конечно, следует производить на диаграмме, но выражать его следует через угол, который будет составлять у наблюдателя на земле соответствующее расстояние в аналемме на небе. Полезно сравнить ее с длиной аналеммы, составляющей 47°. Так, например, если длина экваториального сегмента на диаграмме в 0,4 раза превышает длину аналеммы на диаграмме, то сегмент небесной аналеммы будет стягивать 0,4 × 47 ° = 18,8 ° у наблюдателя на земле. Угол в градусах следует разделить на 15, чтобы получить разницу во времени в часах между восходом солнца и 6 часами утра. Знак разницы виден из диаграммы. Если линия горизонта при восходе Солнца проходит выше начала аналеммы, Солнце восходит до 6 часов утра, и наоборот .

Тот же метод можно использовать с соответствующими изменениями для оценки времени захода солнца. Расчетное время указано по местному времени. Необходимо внести поправки для перевода их в стандартное или летнее время . наблюдателя Эти поправки будут включать в себя термин, включающий долготу , поэтому и широта, и долгота влияют на конечный результат.

Азимуты восхода и захода солнца

Азимуты , где восходит и заходит Солнце , (истинные компасные направления) точек на горизонте можно легко оценить, используя ту же диаграмму, которая используется для определения времени восхода и захода солнца , как описано выше.

Точка, где горизонт пересекает небесный экватор, соответствует востоку или западу. Точка, в которой Солнце находится на восходе или закате, представляет направление восхода или заката. Простое измерение расстояния вдоль горизонта между этими точками в угловом выражении (сравнивая его с длиной аналеммы, как описано выше), дает угол между прямым востоком или западом и направлением восхода или заката. Из диаграммы ясно видно, находится ли восход или закат севернее или южнее восточного или западного направления. Большая петля аналеммы находится на ее южном конце.

Видно с других планет

Аналемма, вид с Марса

На Земле аналемма выглядит как восьмерка , но на других Солнечной системы она может быть совсем другой. телах тела из-за взаимодействия между осевым наклоном , некруглостью его орбиты (что характеризуется эксцентриситетом орбиты ) и углом между северным равноденствием и периапсисом . Наклон имеет тенденцию превращать аналемму в восьмерку, поскольку из-за него фактическое положение Солнца дважды в течение года опережает среднее солнечное время (и, следовательно, также дважды отстает от солнечного времени). Некруглость орбиты имеет тенденцию превращать аналемму в цифру ноль, а положение Солнца опережает среднее солнечное время один раз в году из-за второго закона движения планет Кеплера . В случае Марса сумма двух эффектов дает аналемму каплевидной формы. Юпитер , наклон которого составляет всего 3°, имеет аналемму, имеющую форму эллипса .

Продолжительность: 49 секунд. 0:49

Покадровая съемка аналеммы ​ на Марсе . Создано с использованием изображений MarsDial на марсоходе Opportunity .

В следующем списке день и год относятся к синодическому дню и звездному году конкретного тела:

Меркурий

Поскольку орбитальный резонанс продлевает день ровно на два года, метод построения графика положения Солнца в одно и то же время каждый день даст только одну точку. Однако уравнение времени по-прежнему можно рассчитать для любого времени года, поэтому с помощью этой информации можно построить график аналеммы. Полученная кривая представляет собой почти прямую линию с востока на запад.

Венера

Дней в году чуть меньше двух, поэтому для накопления полной аналеммы обычным способом потребуется несколько лет. Полученная кривая представляет собой эллипс.

Марс

Слезинка.

Юпитер

Эллипс.

Сатурн

Технически это восьмерка, но северная петля настолько мала, что больше напоминает слезинку.

Уран

Восьмерка. (Уран наклонен вбок на угол 98°. Его орбита примерно такая же эксцентричная, как у Юпитера, и более эксцентричная, чем у Земли.)

Нептун

Восьмерка.

О геосинхронных спутниках

Путь геосинхронной орбиты QZSS . Если смотреть с земли, его аналемма будет иметь аналогичную форму.

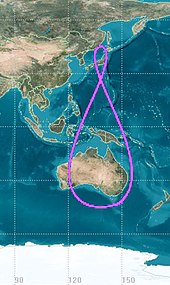
Геосинхронные спутники обращаются вокруг Земли с периодом в один звездный день . Если смотреть с фиксированной точки на поверхности Земли, они прослеживают пути в небе, которые повторяются каждый день, и поэтому представляют собой простые и содержательные аналеммы. Обычно они имеют примерно эллиптическую, каплевидную форму или форму восьмерки. Их форма и размеры зависят от параметров орбит. Подмножеством геосинхронных спутников являются геостационарные спутники , которые в идеале имеют идеально круговые орбиты, расположенные точно в экваториальной плоскости Земли. Таким образом, геостационарный спутник в идеале остается неподвижным относительно поверхности Земли, находясь над одной точкой на экваторе. Ни один настоящий спутник не является строго геостационарным, поэтому настоящие спутники прорисовывают в небе небольшие аналеммы. Поскольку размеры орбит геосинхронных спутников аналогичны размерам Земли, возникает существенный параллакс в зависимости от положения наблюдателя на поверхности Земли, поэтому наблюдатели в разных местах видят разные аналеммы.

Параболоидным антеннам, которые используются для радиосвязи с геосинхронными спутниками, часто приходится перемещаться, чтобы следить за ежедневным движением спутника вокруг его аналеммы. Поэтому механизмы, приводящие их в движение, должны быть запрограммированы с учетом параметров аналеммы. Исключением являются тарелки, которые используются с (приблизительно) геостационарными спутниками, поскольку эти спутники перемещаются настолько мало, что фиксированная тарелка может всегда адекватно функционировать.

О квазиспутниках

Орбитальная схема квазиспутника

Квазиспутник ) , подобный показанному на этой схеме, движется по прямой орбите вокруг Солнца с тем же периодом обращения (который также называется годом), что и сопровождающая его планета, но с другим (обычно большим эксцентриситет орбиты. Если смотреть с планеты, кажется, что он вращается вокруг планеты один раз в год в ретроградном направлении, но с различной скоростью и, вероятно, не в плоскости эклиптики. Относительно своего среднего положения, двигаясь с постоянной скоростью по эклиптике, квазиспутник следует за аналеммой на небе планеты, совершая оборот вокруг нее один раз в год.

См. также

• Анафем
• Армиллярная сфера
• Об архитектуре
• Эпицикл
• Лемниската
• О Диоптре

Дальнейшее чтение

• Оливер, Бернард М. (1972). «Форма аналеммы». Небо и телескоп . 44 : 20. Бибкод : 1972S&T....44...20O .
• Киттлер, Ричард; Дарула, Стэн (2005). «Аналемма, древний набросок вымышленной геометрии солнечной тропы - Солнце, время и история математики». Обзор архитектурной науки . 47 (2): 141–4. дои : 10.1080/00038628.2004.9697037 . S2CID   122005748 .
• Сидоли, Натан (2005). «Методы диоптры 35 Герона и аналеммы: астрономическое определение расстояния между двумя городами». Центавр . 47 (3): 236–58. Бибкод : 2005Cent...47..236S . дои : 10.1111/j.1600-0498.2005.470304.x .
• Семацци, Фредрик Х.М.; Скроггс, Джеффри С.; Пулио, Джордж А.; Макки-Берроуз, Аналемма Лея; Норман, Мэтью; Пуджари, Викрам; Цай, Ю-Мин (2005). «О точности полулагранжевого численного моделирования движения внутренних гравитационных волн в атмосфере» . Журнал Метеорологического общества Японии . 83 (5): 851–69. Бибкод : 2005JMeSJ..83..851S . дои : 10.2151/jmsj.83.851 .
• Лаки, П. (1927). «Аналемма Птолемея» [Аналемма Птолемея]. Астрономические новости (на немецком языке). 230 (2): 17–46. Нагрудный код : 1927AN....230...17L . дои : 10.1002/asna.19272300202 .
• Ид, Юсиф (декабрь 1969 г.). «Построение аналеммы для прямого и косого восхождения». Учитель математики . 62 (8): 669–72. дои : 10.5951/MT.62.8.0669 . JSTOR   27958259 .
• Йеу, Тео Шин (2002). Аналемма для людей с ограниченными возможностями в широтном направлении (PDF) (Диссертация бакалавра). Национальный университет Сингапура. Архивировано из оригинала (PDF) 17 мая 2011 г. Проверено 5 февраля 2006 г.

Внешние ссылки

• Серия «Аналемма» от восхода до заката
• Фотография дня в области науки о Земле (22 января 2005 г.)
• Уравнение времени и аналемма — Кирон Тейлор
• Использование аналеммы - из вставки из «Новой и точной карты мира» Боулза (1780 г.)
• Фигура восемь в небе — содержит ссылку на программу на языке C, использующую более точную формулу, чем большинство других (особенно при больших наклонах и эксцентриситетах).
• Analemma.com — посвящен аналемме.
• Вычислите и нанесите на карту аналемму - веб-сайт, предлагаемый планетарием государственных школ округа Фэрфакс , на котором описывается аналемма, а также предлагается загружаемая электронная таблица, которая позволяет пользователю экспериментировать с аналеммами различной формы.
• Аплет Analemma Sundial — включает в себя множество справочных таблиц.
• Аналеммы — Стивен Вольфрам на основе программы Майкла Тротта, Wolfram Demonstrations Project .
• Аналемма в стихах Тэда Данна
• Создание тутулеммы Тунч Тезеля
• Создание аналеммы солярографии Мацея Запёра и Лукаша Файфровского
• Equation-of-Time.info - многостраничный сайт с множеством иллюстраций и видео, посвященный Уравнению Времени, его компонентам, его истории, способам его отображения в таблицах, кривых, аналеммах и т. д., его использованию для коррекции солнечных часов, астрономия, часы, способы их производства механическим путем и многое другое: Кевин Карни
• Земля и Солнце — интерактивная запись в блоге, объясняющая это явление
• Астрономическая картина дня
  • 09.07.2002 — Аналемма
  • 2003-03-20 — Санрайз Аналемма
  • 2004-06-21 — Аналемма над древней Немеей
  • 2005-07-13 — Аналемма Луны
  • 2006-12-23 — Аналемма над храмом Зевса Олимпийского
  • 30 декабря 2006 г. - Марсианская Аналемма на Мемориальной станции Саган (смоделировано)
  • 2007-06-17 — Аналемма над Украиной
  • 2007-12-04 — Аналемма над Нью-Джерси (фильм)
  • 2008-12-21 — Аналемма над Девичьим крыльцом
  • 2009-12-20 — Тутулемма: Аналемма солнечного затмения
  • 2010-12-31 — Аналемма 2010
  • 20.09.2012 — Sunrise Analemma (с небольшим дополнением)
  • 14.10.2013 — Аналемма в полдень над Азербайджаном
  • 20.03.2014 — Аналемма Солярографии