Измерение расстояния

Меры расстояния используются в физической космологии, чтобы дать естественное представление о расстоянии между двумя объектами или событиями во Вселенной . Их часто используют для привязки некоторой наблюдаемой величины (например, светимости далекого квазара , красного смещения далекой галактики или углового размера акустических пиков в спектре мощности космического микроволнового фона (CMB)) с другой величиной, которая не наблюдаем непосредственно , но более удобен для вычислений (например, сопутствующие координаты квазара, галактики и т. д.). Все обсуждаемые здесь меры расстояния сводятся к общему понятию евклидова расстояния при низком красном смещении.

В соответствии с нашим нынешним пониманием космологии, эти меры рассчитываются в контексте общей теории относительности , где Фридмана-Леметра-Робертсона-Уокера для описания Вселенной используется решение .

Обзор

В космологии существует несколько различных определений «расстояния», которые асимптотичны друг другу для небольших красных смещений . Выражения для этих расстояний наиболее практичны, если они записаны как функции красного смещения. $z$ , поскольку красное смещение всегда является наблюдаемым. Их также можно записать как функции масштабного коэффициента. $a=1/(1+z).$

В оставшейся части статьи пекулярная скорость предполагается пренебрежимо малой, если не указано иное.

Сначала мы приведем формулы для нескольких мер расстояния, а затем опишем их более подробно ниже. Определение «расстояния Хаббла» как $d_{H}={\frac {c}{H_{0}}}\approx 3000h^{-1}{\text{Mpc}}\approx 9.26\cdot 10^{25}h^{-1}{\text{m}}$ где $c$ это скорость света , $H_{0}$ — сегодняшний параметр Хаббла, а $h$ — безразмерная постоянная Хаббла , все расстояния асимптотичны $z\cdot d_{H}$ для малого $z$ .

Согласно уравнениям Фридмана мы также определяем безразмерный параметр Хаббла : ^[1] $E(z)={\frac {H(z)}{H_{0}}}={\sqrt {\Omega _{r}(1+z)^{4}+\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }}}$

Здесь, $\Omega _{r},\Omega _{m},$ и $\Omega _{\Lambda }$ являются нормализованными значениями текущей плотности энергии излучения, плотности материи и « плотности темной энергии » соответственно (последняя представляет собой космологическую постоянную ), и $\Omega _{k}=1-\Omega _{r}-\Omega _{m}-\Omega _{\Lambda }$ определяет кривизну. Тогда параметр Хаббла при данном красном смещении равен $H(z)=H_{0}E(z)$ .

Формула сопутствующего расстояния, которая служит основой для большинства других формул, включает в себя интеграл . Хотя для некоторого ограниченного выбора параметров (см. ниже) интеграл сопутствующего расстояния имеет замкнутую аналитическую форму, в целом — и конкретно для параметров нашей Вселенной — мы можем найти решение только численно . Космологи обычно используют следующие меры для определения расстояний от наблюдателя до объекта с красным смещением. $z$ по линии визирования (LOS): ^[2]

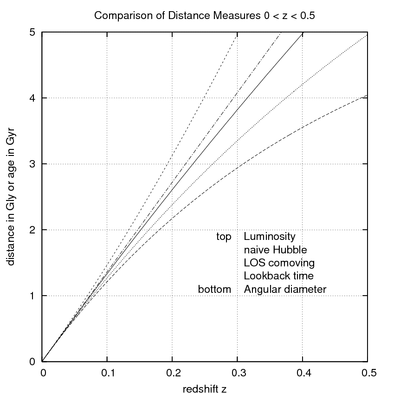
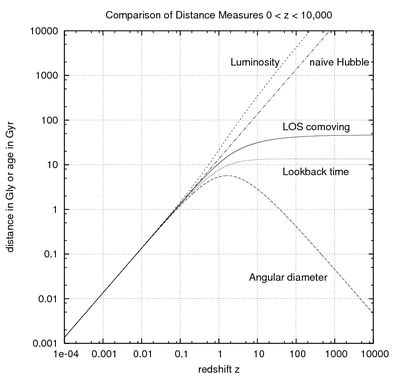
Расстояние перемещения: $d_{C}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{E(z')}}$
Поперечное встречное расстояние: $d_{M}(z)={\begin{cases}{\frac {d_{H}}{\sqrt {\Omega _{k}}}}\sinh \left({\frac {{\sqrt {\Omega _{k}}}d_{C}(z)}{d_{H}}}\right)&\Omega _{k}>0\\d_{C}(z)&\Omega _{k}=0\\{\frac {d_{H}}{\sqrt {|\Omega _{k}|}}}\sin \left({\frac {{\sqrt {|\Omega _{k}|}}d_{C}(z)}{d_{H}}}\right)&\Omega _{k}<0\end{cases}}$
Расстояние углового диаметра: $d_{A}(z)={\frac {d_{M}(z)}{1+z}}$
Расстояние освещенности: $d_{L}(z)=(1+z)d_{M}(z)$
Расстояние светового путешествия: $d_{T}(z)=d_{H}\int _{0}^{z}{\frac {dz'}{(1+z')E(z')}}$

Альтернативная терминология

Пиблз называет поперечное сопутствующее расстояние «расстоянием углового размера», которое не следует путать с расстоянием углового диаметра. ^[1] Иногда символы $\chi$ или $r$ используются для обозначения как сопутствующего, так и углового диаметра расстояния. Иногда расстояние прохождения света также называют «расстоянием обратного обзора» и/или «временем обратного обзора». ^{[ нужна ссылка ]}

Подробности

Своеобразная скорость

движение Земли относительно потока Хаббла . В реальных наблюдениях на наблюдаемое красное смещение влияет ^{[ нужна ссылка ]}

На самом деле существует два понятия красного смещения. Одним из них является красное смещение, которое наблюдалось бы, если бы и Земля, и объект не двигались относительно «движущегося» окружения ( поток Хаббла ), определяемого космическим микроволновым фоном. Другой — это фактическое измеренное красное смещение, которое зависит как от пекулярной скорости наблюдаемого объекта, так и от его пекулярной скорости. Поскольку Солнечная система движется со скоростью около 370 км/с в направлении между Львом и Кратером , это уменьшает $1+z$ для удаленных объектов в этом направлении примерно в 1,0012 раза и увеличивает его в такой же раз для удаленных объектов в противоположном направлении. (Скорость движения Земли вокруг Солнца всего 30 км/с.) ^{[ нужна ссылка ]}

Расстояние перемещения

Предстоящее расстояние $d_{C}$ между фундаментальными наблюдателями, то есть наблюдателями, которые оба движутся вместе с потоком Хаббла , не меняется со временем, поскольку сопутствующее расстояние объясняет расширение Вселенной. Сопутствующее расстояние получается путем интегрирования правильных расстояний до ближайших фундаментальных наблюдателей вдоль луча зрения ( LOS ), тогда как правильное расстояние — это то, что дало бы измерение в постоянное космическое время. ^{[ нужна ссылка ]}

В стандартной космологии сопутствующее расстояние и собственное расстояние — это две тесно связанные меры расстояния, используемые космологами для измерения расстояний между объектами; Сопутствующее расстояние — это правильное расстояние в настоящее время. ^{[ нужна ссылка ]}

Сопутствующее расстояние (с небольшой поправкой на наше собственное движение) — это расстояние, которое можно было бы получить из параллакса, поскольку параллакс в градусах равен отношению астрономической единицы к длине окружности, проходящей в настоящее время через Солнце и по центру удаленного объекта, умноженный на 360°. Однако объекты, превышающие мегапарсек, имеют параллакс слишком мал, чтобы его можно было измерить ( космический телескоп Gaia измеряет параллакс ярчайших звезд с точностью до 7 микросекунд дуги), поэтому параллакс галактик за пределами нашей Местной группы слишком мал, чтобы его можно было измерить.

Существует выражение в замкнутой форме для интеграла в определении сопутствующего расстояния, если $\Omega _{r}=\Omega _{m}=0$ или, заменив масштабный коэффициент $a$ для $1/(1+z)$ , если $\Omega _{\Lambda }=0$ . Наша Вселенная теперь, кажется, тесно представлена $\Omega _{r}=\Omega _{k}=0.$ В этом случае мы имеем: $d_{C}(z)=d_{H}\Omega _{m}^{-1/3}\Omega _{\Lambda }^{-1/6}[f((1+z)(\Omega _{m}/\Omega _{\Lambda })^{1/3})-f((\Omega _{m}/\Omega _{\Lambda })^{1/3})]$ где $f(x)\equiv \int _{0}^{x}{\frac {dx}{\sqrt {x^{3}+1}}}$

Сопутствующее расстояние следует рассчитывать, используя значение $z$ , которое имело бы место, если бы ни объект, ни мы не имели своеобразной скорости.

Вместе с масштабным коэффициентом он дает правильное расстояние до объекта, когда свет, который мы видим сейчас, был испущен им и направился к нам: $d=ad_{C}$

Правильное расстояние

Правильное расстояние примерно соответствует тому, где удаленный объект будет находиться в определенный момент космологического времени , который может меняться со временем из-за расширения Вселенной . Сопутствующее расстояние учитывает расширение Вселенной, что дает расстояние, которое не меняется во времени из-за расширения пространства (хотя оно может измениться из-за других, локальных факторов, таких как движение галактики внутри скопления); Сопутствующее расстояние — это правильное расстояние в настоящее время. ^{[ нужна ссылка ]}

Поперечное встречное расстояние

Два сопутствующих объекта с постоянным красным смещением $z$ которые разделены углом $\delta \theta$ Говорят, что на небе есть расстояние $\delta \theta d_{M}(z)$ , где поперечное сопутствующее расстояние $d_{M}$ определяется соответствующим образом. ^{[ нужна ссылка ]}

Расстояние углового диаметра

Объект размером $x$ на красном смещении $z$ похоже, имеет угловой размер $\delta \theta$ имеет угловое расстояние диаметра $d_{A}(z)=x/\delta \theta$ . Это обычно используется для наблюдения за так называемыми стандартными линейками , например, в контексте барионных акустических колебаний .

При учете пекулярной скорости Земли следует использовать красное смещение, которое имело бы место в этом случае, но $d_{A}$ следует внести поправку на движение Солнечной системы с коэффициентом от 0,99867 до 1,00133, в зависимости от направления. (Если начать двигаться со скоростью $v$ к объекту на любом расстоянии, угловой диаметр этого объекта уменьшится в раз. ${\textstyle {\sqrt {(1+v/c)/(1-v/c)}}.}$ )

Расстояние освещенности

Если собственная светимость $L$ удаленного объекта, мы можем вычислить расстояние его светимости, измерив поток $S$ и определить ${\textstyle d_{L}(z)={\sqrt {L/4\pi S}}}$ , что оказывается эквивалентным приведенному выше выражению для $d_{L}(z)$ . Эта величина важна для измерения стандартных свечей, таких как сверхновые типа Ia , которые впервые были использованы для открытия ускорения расширения Вселенной .

При учете пекулярной скорости Земли красное смещение, которое имело бы место в этом случае, следует использовать для $d_{M},$ но фактор $(1+z)$ следует использовать измеренное красное смещение и внести еще одну поправку на пекулярную скорость объекта, умножив ее на ${\textstyle {\sqrt {(1+v/c)/(1-v/c)}},}$ где теперь $v$ — составляющая пекулярной скорости объекта вдали от нас. Таким образом, расстояние светимости будет равно расстоянию углового диаметра, умноженному на $(1+z)^{2},$ где $z$ — измеренное красное смещение в соответствии с теоремой взаимности Этерингтона (см. ниже).

Расстояние светового путешествия

(также известное как « время ретроспективного анализа » или « расстояние ретроспективного анализа ») ^[3]

Это расстояние $d_{T}$ это время, за которое свет достиг наблюдателя от объекта, умноженное на скорость света . Например, радиус наблюдаемой Вселенной в этой мере расстояния равен возрасту Вселенной, умноженному на скорость света (1 световой год/год), что оказывается примерно 13,8 миллиарда световых лет. ^{[ нужна ссылка ]}

Существует решение в замкнутой форме расстояния прохождения света, если $\Omega _{r}=\Omega _{m}=0$ с участием обратных гиперболических функций ${\text{arcosh}}$ или ${\text{arsinh}}$ (или с использованием обратных тригонометрических функций , если космологическая постоянная имеет другой знак). Если $\Omega _{r}=\Omega _{\Lambda }=0$ то существует решение в замкнутой форме для $d_{T}(z)$ но не для $z(d_{T}).$

Обратите внимание, что сопутствующее расстояние восстанавливается из поперечного сопутствующего расстояния путем принятия предела $\Omega _{k}\to 0$ , так что две меры расстояния эквивалентны в плоской Вселенной .

Существуют веб-сайты для расчета расстояния прохождения света по красному смещению. ^[4]^[5]^[6]^[7]

Тогда возраст Вселенной станет $\lim _{z\to \infty }d_{T}(z)/c$ , и время, прошедшее с момента красного смещения $z$ до сих пор это: $t(z)=d_{T}(z)/c.$

Дистанционная двойственность Этерингтона

Уравнение дистанционной двойственности Этерингтона ^[8] - это соотношение между расстоянием светимости стандартных свечей и расстоянием углового диаметра. Это выражается следующим образом: $d_{L}=(1+z)^{2}d_{A}$

См. также

Ссылки

^ Jump up to: ^а ^б Пиблс, PJE (1993). Принципы физической космологии . Издательство Принстонского университета . стр. 310–320 . Бибкод : 1993ppc..книга.....P . ISBN 978-0-691-01933-8 .
^ Дэвид В. Хогг (2000). «Дистанционные меры в космологии». arXiv : astro-ph/9905116v4 .
^ Персонал (2022 г.). «Космологический калькулятор» . Международный центр радиоастрономических исследований . Проверено 4 августа 2022 г.
^ Персонал (2015). «Космологический калькулятор Калифорнийского университета в Лос-Анджелесе» . Калифорнийский университет в Лос-Анджелесе . Проверено 6 августа 2022 г. Расстояние прохождения света было рассчитано на основе значения красного смещения с использованием Космологического калькулятора Калифорнийского университета в Лос-Анджелесе со значениями параметров по состоянию на 2015 год: H ₀ = 67,74 и Omega _M = 0,3089 (см. Таблицу / Planck2015 в разделе « Модель Lambda-CDM # Параметры »).
^ Персонал (2018). «Космологический калькулятор Калифорнийского университета в Лос-Анджелесе» . Калифорнийский университет в Лос-Анджелесе . Проверено 6 августа 2022 г. Расстояние прохождения света было рассчитано на основе значения красного смещения с использованием Космологического калькулятора Калифорнийского университета в Лос-Анджелесе со значениями параметров по состоянию на 2018 год: H ₀ = 67,4 и Omega _M = 0,315 (см. Таблицу / Planck2018 в разделе « Модель Lambda-CDM # Параметры »).
^ Персонал (2022 г.). «Космологический калькулятор ICRAR» . Международный центр радиоастрономических исследований . Проверено 6 августа 2022 г. Космологический калькулятор ICRAR - установите H ₀ = 67,4 и Omega _M = 0,315 (см. Таблицу / Planck2018 в разделе « Модель Lambda-CDM # Параметры »).
^ Кемпнер, Джошуа (2022). «Космологический калькулятор КЕМПНЕРА» . Кемпнер.нет . Проверено 6 августа 2022 г. Космологический калькулятор KEMP — установите H ₀ = 67,4, Omega _M = 0,315 и Omega _Λ = 0,6847 (см. Таблицу/Planck2018 в разделе « Модель Lambda-CDM # Параметры »).
^ IMH Этерингтон, «LX. Об определении расстояния вОбщая теория относительности», Философский журнал, Vol. 15, С. 7 (1933), стр. 761-773.

Скотт Додельсон, Современная космология. Академическое издательство (2003).

Внешние ссылки

«Шкала расстояний Вселенной» сравнивает различные космологические меры расстояний.
«Меры расстояний в космологии» подробно объясняет, как рассчитать различные меры расстояний в зависимости от модели мира и красного смещения.
iCosmos: космологический калькулятор (с генерацией графиков) вычисляет различные меры расстояния в зависимости от космологической модели и красного смещения и создает графики для модели от красного смещения от 0 до 20.

[peebles1993-1] Jump up to: ^а ^б Пиблс, PJE (1993). Принципы физической космологии . Издательство Принстонского университета . стр. 310–320 . Бибкод : 1993ppc..книга.....P . ISBN 978-0-691-01933-8 .

[Hogg-2] Дэвид В. Хогг (2000). «Дистанционные меры в космологии». arXiv : astro-ph/9905116v4 .

[CALC-2022-3] Персонал (2022 г.). «Космологический калькулятор» . Международный центр радиоастрономических исследований . Проверено 4 августа 2022 г.

[UCLA-2015-4] Персонал (2015). «Космологический калькулятор Калифорнийского университета в Лос-Анджелесе» . Калифорнийский университет в Лос-Анджелесе . Проверено 6 августа 2022 г. Расстояние прохождения света было рассчитано на основе значения красного смещения с использованием Космологического калькулятора Калифорнийского университета в Лос-Анджелесе со значениями параметров по состоянию на 2015 год: H ₀ = 67,74 и Omega _M = 0,3089 (см. Таблицу / Planck2015 в разделе « Модель Lambda-CDM # Параметры »).

[UCLA-2018-5] Персонал (2018). «Космологический калькулятор Калифорнийского университета в Лос-Анджелесе» . Калифорнийский университет в Лос-Анджелесе . Проверено 6 августа 2022 г. Расстояние прохождения света было рассчитано на основе значения красного смещения с использованием Космологического калькулятора Калифорнийского университета в Лос-Анджелесе со значениями параметров по состоянию на 2018 год: H ₀ = 67,4 и Omega _M = 0,315 (см. Таблицу / Planck2018 в разделе « Модель Lambda-CDM # Параметры »).

[ICRAR-2022-6] Персонал (2022 г.). «Космологический калькулятор ICRAR» . Международный центр радиоастрономических исследований . Проверено 6 августа 2022 г. Космологический калькулятор ICRAR - установите H ₀ = 67,4 и Omega _M = 0,315 (см. Таблицу / Planck2018 в разделе « Модель Lambda-CDM # Параметры »).

[KEMP-2022-7] Кемпнер, Джошуа (2022). «Космологический калькулятор КЕМПНЕРА» . Кемпнер.нет . Проверено 6 августа 2022 г. Космологический калькулятор KEMP — установите H ₀ = 67,4, Omega _M = 0,315 и Omega _Λ = 0,6847 (см. Таблицу/Planck2018 в разделе « Модель Lambda-CDM # Параметры »).

[8] IMH Этерингтон, «LX. Об определении расстояния вОбщая теория относительности», Философский журнал, Vol. 15, С. 7 (1933), стр. 761-773.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]