Перекрещенный пятиугольный куплоид
| Перекрещенный пятиугольный куплоид | |
|---|---|
 | |
| Лица | 5 треугольников 5 квадратов 1 пятиугольник |
| Края | 20 |
| Вершины | 10 |
| Конфигурация вершин | 5(5.4. 3 / 2 .4) 5(3.4. 3 / 2 . 4 / 3 ) |
| Группа симметрии | С 5в , [5], (*55) |
| Группа вращения | С 5 , [5] + , (55) |
| Двойной многогранник | скрещенный пятиугольный кератиноид |
| Характеристики | неориентируемый |

В геометрии или скрещенный пятиугольный куплоид скрещенный пятиугольный полукупол — один из членов бесконечного семейства куплоидов . Его можно получить как срез большого сложного ромбикосододекаэдра . Как и во всех куполах , базовый многоугольник имеет в два раза больше ребер и вершин , чем верхний; но в этом случае базовый многоугольник представляет собой вырожденный { 10 / 4 } декаграмм , так как вершина — { 5/4 } пятиугольник . Следовательно, вырожденное основание удаляется, а треугольники вместо этого соединяются с квадратами.
Его можно рассматривать как купол с ретроградным пятиугольным основанием, так что квадраты и треугольники соединяются через основания в противоположном направлении по отношению к пятиугольному куполу , следовательно, пересекая друг друга.
Связанные многогранники
[ редактировать ]| 3 | 5 | 7 | n ⁄ d |
|---|---|---|---|
 {3/2} Перекрещенный треугольный куплоид (с ног на голову) |  {5/2} Пентаграммный куплоид |  {7/2} Гептаграммный куплоид | 2 |
| — |  {5/4} Перекрещенный пятиугольный куплоид (с ног на голову) |  {7/4} Перекрещенный гептаграммный куплоид | 4 |
Скрещенный пятиугольный куплоид можно рассматривать как сечение вырожденного однородного многогранника, известного как большой комплексный ромбикосидодекаэдр :
 Перекрещенный пятиугольный куплоид |  Большой сложный ромбокосододекаэдр | ||
 Малый дитригональный икосододекаэдр |  Дитригональный додекадодекаэдр |  Большой дитригональный икосододекаэдр |  Соединение пяти кубиков |
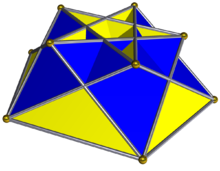
(На изображении скрещенного пятиугольного куплоида пятиугольник красный (внизу и не виден), квадраты желтые, а треугольники синие. На изображении малого сложного ромбокосододекаэдра пятиугольники красные, квадраты синие ( спрятаны внутри и не видны), а треугольники желтые.)
Взяв один пятиугольник из большого сложного ромбокосододекаэдра, затем взяв пять соседних с ним квадратов, а затем взяв пять треугольников, граничащих с этими квадратами, мы получим скрещенный пятиугольный куплоид. Поскольку этот скрещенный пятиугольный куплоид, таким образом, разделяет все свои ребра с этим многогранником, его можно назвать реберной огранкой его . Невырожденные однородные многогранники, имеющие те же ребра, что и небольшой комплексный ромбокосидодекаэдр, представляют собой три двутригональных многогранника , а также правильное соединение пяти кубов : следовательно, скрещенный пятиугольный куплоид также является огранкой ребер этих многогранников.
Как 5 / 4 < 2, скрещенный пятиугольный куплоид не имеет мембраны, как пентаграммный куплоид.
Двойной многогранник
[ редактировать ]
Двойник скрещенного пятиугольного куплоида имеет 5 воздушных змеев и 5 антипараллелограммных граней и может быть назван скрещенным пятиугольным кератиноидом в честь Инчбальда, поскольку он имеет форму полого рога:
Ссылки
[ редактировать ]- Гай Инчбальд, Заполнение многогранников
- Ричард Клитцинг, Осесимметричные грани однородных многогранников
- Джим Макнил, Полукупол 5/2 и полукупол 5/4
- Джим Макнил, Semicupolas
- Ульрих Микловайт, Огранки однородных многогранников.
